小口径尾翼弹膛口流场数值模拟
2021-07-08戴劲松王茂森林圣业
汤 傲,戴劲松,王茂森,何 福,林圣业
(南京理工大学, 南京 210094)
膛口流场是非定常、带有强激波间断的复杂流场[1-2]。在火炮射击的后效期,高温高压燃气迅速释放,膛口周围出现各种复杂的物理和化学现象,膛口附近形成了复杂的瞬态膛口流场波系结构,产生强激波、电磁辐射和膛口焰等扰动并对人员设备等产生危害[3]。带尾翼稳定装置的弹丸,其尾翼在后效期张开过程中会受到膛口流场的强烈扰动,特别是膛口流场不对称分布时常常造成弹丸及尾翼受力不对称,致使弹丸不能正常飞行[4]。因此,对带尾翼装置弹丸的膛口流场进行数值模拟,对尾翼的结构设计及后效期张开的研究具有重要意义。目前,随着计算机运算能力的提升,膛口流场数值模拟有了很大的进步,对膛口流场的研究逐步向三维、高精度格式、包含运动弹丸等趋势发展[5]。焦志刚等[6]应用动网格技术划分网格,针对带稳定装置的弹丸发射时形成的膛口流场进行数值模拟计算并分析气流速度、压力的分布规律和对尾翼受力情况的影响;岳明凯等[7]使用FLUENT 局部重构法,对弹丸飞出制退器以及尾翼张开过程的膛口流场进行数值模拟并分析了膛口流场对尾翼受力状况和运动状态的影响。上述这些研究对象主要集中在100 mm口径以上的大口径弹丸上,采用的方法以动网格法等为主。本文采用重叠网格法,对60 mm口径以下的小口径尾翼弹丸出膛口及尾翼展开过程进行了仿真并分析了弹丸出膛口后尾翼张开过程中速度压力云图随时间的变化情况。此外,本文还研究了不同初始偏角情况下弹丸径向受力和径向位移的规律,为小口径尾翼弹的设计和试验提供了一定依据。
1 数值计算方法
本文研究的小口径尾翼弹,其尾翼装置在膛内运动时收束在弹后,在出膛口后迅速展开,相对大口径弹丸和一般的小口径尾翼弹其特殊性在于:① 对射速要求不高;② 具有相对较低的膛口初速和较低的平均膛压;③ 弹丸的长细比较大。由于建立一个全面的膛口流场数学模型极为困难,因此结合弹丸特点进行以下简化[8]:
1) 忽略火药气体多组分和化学反应的影响,将大气视为理想气体;
2) 忽略弹带弹丸定心部等复杂结构,对弹丸及尾翼装置进行一定程度的简化。
根据以上基本假设,以三维笛卡尔坐标系下可压缩气体粘性流动的 N-S 方程为数学计算模型[9]:
(1)
式中:U=[ρ,ρu,ρv,ρw,E]T
F=[ρu,ρu2+p,ρuv,ρuw, (E+p)u]T
G=[ρv,ρuv,ρv2+p,ρvw, (E+p)u]T
H=[ρw,ρuw,ρvw,ρw2+p, (E+p)v]T
式中,ρ为气体密度;u、v、w分别为x、y和z方向的速度分量;p为气体压强;E为总能量,其表达式为:
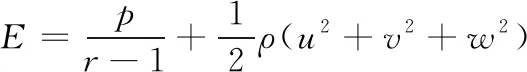
(2)
式中,r为理想气体绝热指数。
理想气体状态方程为
p=ρRT
(3)
式中,R为气体常数;T为热力学温度。
根据火炮膛口流场的特点,采用的标准k-ε模型作为湍流模型[10],其表达式为:
Gk+Gb-ρε-Ym+Sk
(4)
(5)
式中,Gk为由层流速度梯度引起的湍流动能;Gb为由浮力引起的湍流动能;Ym为湍流过渡的扩散产生的波动;σk和σε分别是k方程和ε方程的湍流Prandtl数;C1、C2、C3为系数。
方程的离散采用有限体积法。采用Roe一阶迎风格式将对流项离散为[11]
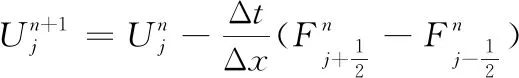
(6)
(7)
2 计算模型及网格划分
本文采用重叠网格法进行仿真计算,重叠网格基本原理是采用两套网格,一套为背景网格,一套为前景(组件)网格。部件运动过程中,系统不断地检测背景网格与前景网格的重合区域,并计算交接界面[12]。
相比动网格等其他处理部件运动的方法,重叠网格法的优点主要体现在以下方面:
1) 简化复杂几何的网格划分,不同计算区域可选择最恰当的网格形式;
2) 有利于相对运动部件的网格生成;特别是本例中可以比较方便地调整尾翼组件的相关参数;
3) 避免了动网格法中网格重构失败等一些问题。
根据重叠网格的原理,对身管及膛口流场划分网格,建立5个前景网格包括一个弹体组件和4个翼片组件,如图1所示,在图1中①表示长度为1.6 m的身管区域,②表示直径为1 000 mm长度为1 m的外流场区域,③表示外流场中心涉及弹丸运动的局部加密区域。
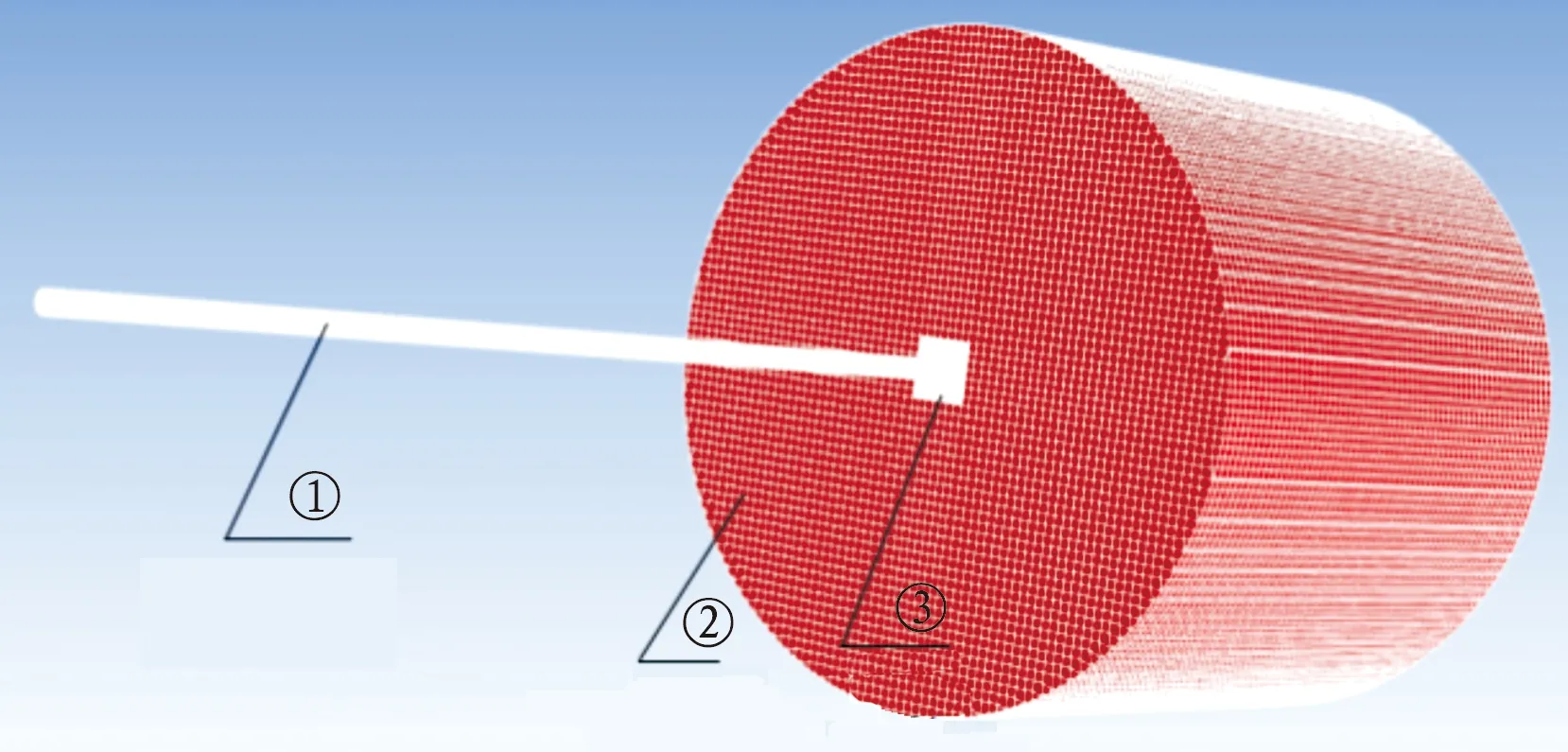
图1 背景网格示意图
对弹体组件及4个翼片组件单独划分网格,组合成完整的弹丸结构如图2所示。

图2 组合后的弹丸网格示意图
给定计算域边界条件:身管、弹体及尾翼设为固壁边界,流场外边界设为压力出口边界。计算初始条件根据某小口径尾翼弹相关内弹道参数建立经典内弹道模型并求解,得到其内弹道曲线如图3~图5所示。
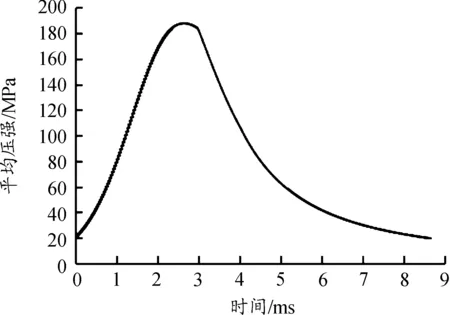
图3 内弹道过程膛压曲线

图4 内弹道过程弹丸速度曲线
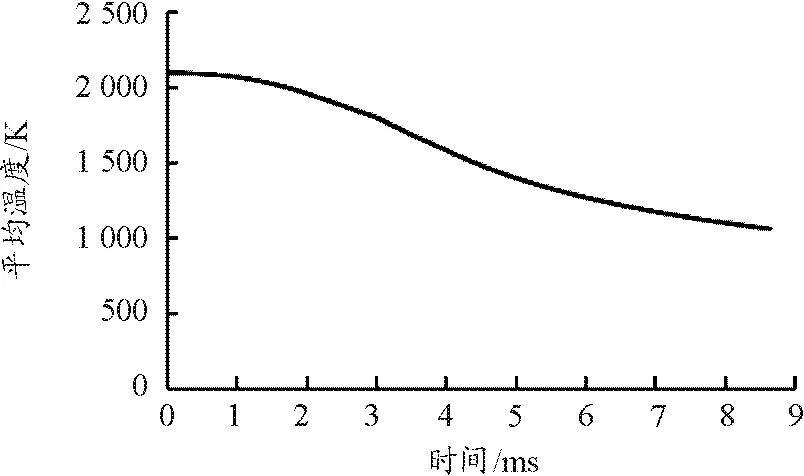
图5 内弹道过程温度曲线
3 仿真结果分析
经过三维仿真计算,得到了尾翼张开过程的流场分布情况如图6~图8所示。其中图6反映了膛口流场速度随时间的变化,图7反映了弹体压力随时间的变化,图8为尾翼张开到位时的三维速度等值线图。
由图6(a)可知,在0~0.25 ms时刻弹丸及尾翼完全脱离身管,尾翼开始展开。高温高压的火药气体出膛口后迅速向外膨胀并初步形成膛口流动主流场,部分火药气体继续作用在弹底并推动弹丸加速前进,还有部分火药气体与高速展开的尾翼装置相互作用:一方面尾翼装置受到分布不均的火药气体作用,由图7(a)可知轴向上尾翼装置尾部受力大于靠近弹底侧受力,而径向上尾翼装置内侧受力大于外侧受力,这说明在该过程中火药气体加速了尾翼的张开过程,而另一方面弹底附近火药气体在包围弹体并向外扩散的途中部分受到了尾翼装置的阻碍,由于此时尾翼刚张开到较小角度,翼片之间较为密集因此减缓了部分火药气体扩散的速度,但是仍有部分火药气体从翼片之间的间隙穿过并向外发展。
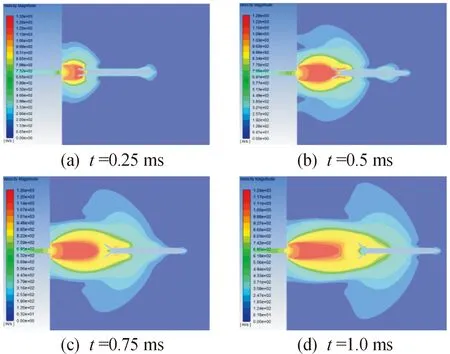
图6 不同时刻膛口流场速度云图
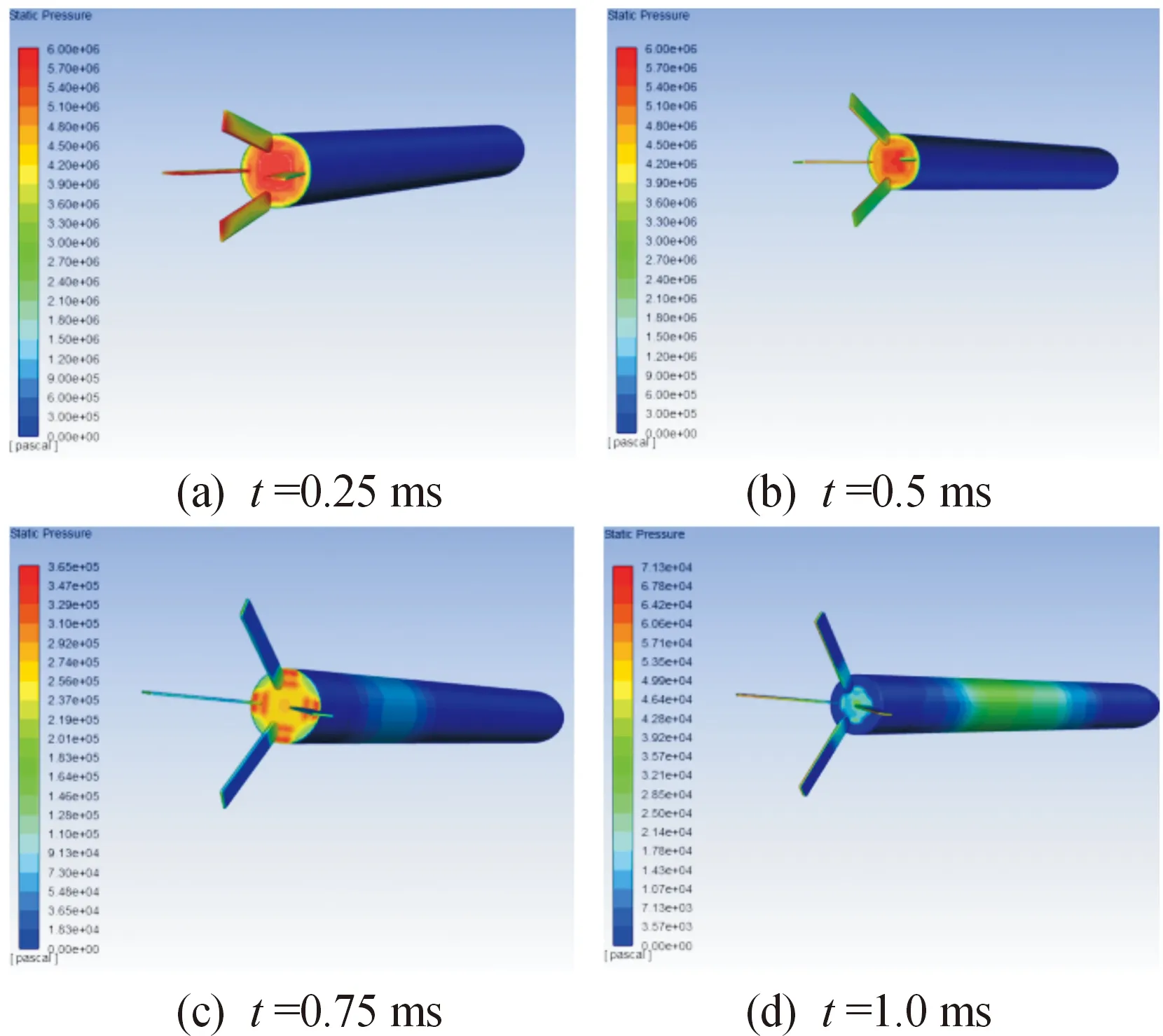
图7 不同时刻弹丸压力云图
由图6(b)~(c)可知,在0.25~0.75 ms时刻火药气体以远超弹丸的速度向外向前膨胀并逐渐包围弹丸,包含典型激波的膛口流场完全形成。与无尾翼张开弹丸膛口流场的区别是,在这个时间段内尾翼进一步展开,大量弹底附近的火药气体得以穿过翼片向前运动同时受到尾翼张开的推力从而获得了更高的速度,因此形成了弹丸尾部与尾翼装置连接区域速度集中的独特现象;而翼片尾部间的距离已经张开至相对较大且没有弹底的阻挡,火药气体得以进一步扩散,与初始冲击波及膛口冲击波互相作用形成复杂的波系结构并向外发展。如图7(b)至图7(c)所示,此时弹丸在火药气体流动的包围之中,弹底及翼片所受压力仍高于弹尖压力,弹丸轴向运动速度略有增加,随着弹丸向前运动,弹丸所受压力迅速降低。
从图6(d)及图8可以很直观的观察到尾翼张开到位时的速度分布,此时膛口冲击波继续向外流场扩散并衰减,炮口附近仍存在速度较高的火药气体,弹底附近激波消失,弹体周围气流速度与弹体飞行速度大致相当。由图7(d)可以发现作用到弹体及尾翼上的压力进一步降低,火药气体不再对弹产生显著的影响。

图8 尾翼张开到位时的速度等值线图
此外,考虑到弹丸在出膛口瞬间的偏角可能会导致弹丸及尾翼装置在径向受力不均甚至可能影响到弹丸的飞行稳定性,因此对弹丸处于不同初始偏角的情况进行了仿真分析,得到了初始偏角为1~4 mrad时弹丸的径向受力随时间变化曲线和对应的弹丸径向位移随时间变化曲线如图9、图10所示。由图9可知,在存在初始偏角的情况下,弹丸径向受力不均且存在明显的振荡,不同偏角情况下振荡的趋势大致一致,偏角每增大1 mrad,径向受力的最大值增大15~20 N 左右。由图10可以得到1~4 mrad情况下弹丸的径向位移,很显然偏角越大径向位移越大,偏角每增大1 mrad,径向位移增大0.003~0.004 mm左右,4 mrad时径向位移达到最大值为0.011 mm左右。
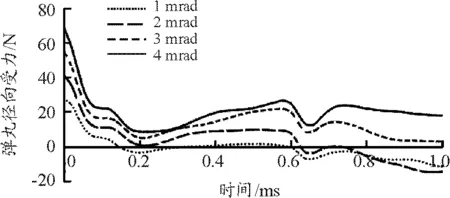
图9 不同初始偏角下弹丸径向受力曲线
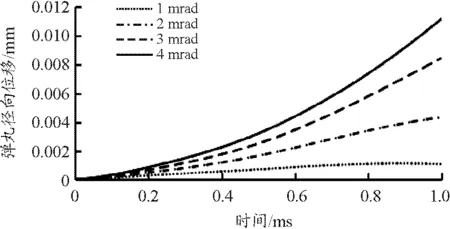
图10 不同初始偏角下弹丸径向位移曲线
4 结论
1) 重叠网格法较好地适应了包括平动和转动的复杂边界运动情况且避免了负体积网格的产生,计算结果清晰地展现了不同时刻膛口流场速度压力等分布情况。
2) 含尾翼张开过程的小口径尾翼弹膛口流场保留了膛口流场的主要特征,在局部区域膛口冲击波与尾翼转动的共同作用会产生更加复杂的激波,在尾翼与弹体连接处附近形成独特的波系结构。
3) 弹丸径向受力的最大值和径向位移随初始偏角的增大而增大,在弹丸存在1~4 mrad初始偏角的情况下,偏角每增大1 mrad,径向受力的最大值增大15~20 N,径向位移增大0.003~0.004 mm,减小弹丸初始偏角有利于减小弹丸扰动,提高弹丸稳定性。
