分布式电推进飞机动力系统评估优化方法
2021-07-07雷涛孔德林王润龙李伟林张晓斌
雷涛,孔德林,王润龙,李伟林,2,张晓斌,2
1. 西北工业大学 自动化学院,西安 710129
2. 飞机电推进技术工信部重点实验室,西安 710129
随着社会的不断发展,飞机逐渐成为人们首选的出行方式,相应地,商业飞机每年的飞行时间与里程数大大增加,由此所带来的化石燃料大量消耗、温室气体排放量增多、噪声污染等问题引起了人们的广泛关注[1-2]。
为了解决燃料过度消耗与环境污染问题,美国国家航空航天局(NASA)于2008年提出了未来20年飞机技术的发展目标。以目前的运输客机技术指标作为基准,将噪音降低71分贝,氮氧化合物排放量降低80%,同时燃料消耗降低70%[3-4]。此外,国际民用航空组织(ICAO)也制定了飞机的发展目标。从2010年到2020年每年提高2%的燃料效率,从2020年开始实现碳中和增长,并将二氧化碳排放量减少50%[5]。为了实现ICAO和NASA提出的发展目标,必须对现有的飞机推进系统进行全方位的改进。
近年来,随着电池、电力电子器件和电机效能的提高,人们开始重新关注使用电力作为飞机主动力的可行性。目前涡轮风扇发动机对燃料产生的化学能的利用率仅有40%左右,而电推进飞机系统对电能的利用率能达到70%[6]。显然,采用电推进飞机系统可以明显减少燃料消耗、噪音产生以及污染物的排放,因此飞机制造商正在研究探索多电飞机(MEA)、混合动力飞机(HEA)等系统来实现动力总成的电气化。
多电飞机系统通过优化非设计点工作规范、消除引气、电动增压等方式提高了发动机性能,同时使用电气系统取代液压系统,在降低了设备重量的同时提高了二次能源和电能利用率。在多电飞机系统中,电池可用于提供负载和应急电源所需的瞬态功率。而在混合动力飞机系统中,电池还可以通过电动机的制动运行状态获得回馈能量。油电混合电推进飞机系统主要以发动机、蓄电池等储能装置和电动机作为飞机动力来源,具有高性能、低能耗和低污染的特点以及技术、经济和环境友好等方面的综合优势。与传统的发动机推进系统和纯电动推进系统相比,油电混合电推进飞机系统中动力系统具有多种组合方式,并能够根据飞行剖面对系统的工作方式做出优化组合,使作为主动力源的发动机能够维持在经济运行区和低排放区工作,以保证飞机良好的动力性、低排放性和低能耗性。虽然油电混合动力系统可以减少燃料消耗并改善对环境的影响,但同时也带来了一些缺点,例如系统的复杂性更高,增加配电系统导致飞机整体的体积和质量增大,以及推进功率较高时电气系统可能存在的可靠性等问题。
电推进飞机系统使用电能产生所需的动力,因此需要电能装置提供足够的推进功率,目前电推进飞机的推进功率等级从数十千瓦到几十兆瓦不等[7],根据推进功率的不同,动力系统所选用的架构也有所不同。小功率的电推进飞机主要被应用在无人机与短途飞行的商用单双座飞机场合,在这种场景下,只使用电池作为推力来源的纯电推进系统架构有着更大的优势;对于兆瓦级电推进飞机,受限于电池的容量,需要采用涡轮发电机与电池组共同为飞机推进器提供能量来源。
目前电推进混合动力系统在汽车、船舶等方面应用较为广泛,而对于飞机混合动力系统的研究起步则较晚,在充分吸取汽车、船舶领域的研究经验后,目前国外航空领域也在逐步研究开发电推进飞机混合动力系统的概念设计工具,并提出了多种评估优化方法。
有学者采用一种为电气系统各部件设定固定的效率来分析各部件的功率损失情况的方法来获得电气系统的功率损失[8-9],尽管这种方法提供了快速的系统分析能力,但可能缺少对电力系统重要性能的评估。文献[10]将地面交流电网中经常使用的功率流分析方法应用到电推进飞机系统的概念设计中,建立了电气系统各部件的数学模型,并对一种涡轮电动倾斜翼飞机的配电系统进行了分析,得到配电系统在稳定运行状态与断路状态下的电网电压电流分布情况。虽然文献[10]对电推进飞机配电系统进行了较为准确的分析,但是没有与机械部件进行对接,不能够对完整的动力系统进行分析。文献[11]提出了一种基于功率/负载流建模的电推进飞机动力系统电气部件建模仿真方法,该方法建立了电气系统的准静态模型,用来预测系统的稳态性能,以及控制系统的动态相应。这种电气建模方案基于MATLAB/SIMULINK平台,将电气系统模型与用热力学系统建模和分析工具箱(T-MATS)创建的发动机模型集成在一起,解决了创建电推进飞机动力系统的系统级模型时存在的两大问题,如何保证电能传输的效率,以及电气系统的动态如何影响非电气部件。
如前文中所提到的,混合动力推进技术在汽车与船舶领域已经得到了广泛的应用,因此也早已开发出了相关的建模与优化工具,例如用于评估混合动力汽车对环境产生的影响与汽车性能的软件Advisor[12]与AVL Cruise[13]等,这些仿真工具对动力系统的每个部件采用统一的模型方法[14],并采用后向仿真方法(假设已知驾驶条件,计算车辆的瞬时动力要求以满足驾驶条件)对动力系统进行评估与优化。仿照这种建模方法,文献[15]介绍了用于复杂飞机动力系统设计和优化的模拟方法,在此基础上,文献[16]基于多学科方法,综合考虑了飞行力学、空气动力学与热力学等多种约束条件,建立了动力系统各部件尺寸与功率模型,开发出了用于评估传统飞机和电推进飞机架构的性能、成本和环境影响的仿真软件。文献[17]在MATLAB环境下开发了一种用于确定电推进飞机动力系统架构尺寸的设计软件,该软件通过输入电动机的需求转速与转矩,计算出动力系统各部件的物理尺寸与重量,以及系统的功率损失与效率,该软件是基于STARC-ABL电推进飞机架构而设计的,没有考虑进储能装置对动力系统的影响。
文献[18]提出了一种针对电力电子变换器的重量优化设计方法,采用多种分层权重优化设计算法解决设计变量识别和设计交互解耦过程中的困难,具体包括诸如遗传算法(GA)、粒子群优化(PSO)和模拟退火(SA)此类的元启发式优化方法。文献[19]介绍了符号规划(SP)在电力推进系统评估和多学科优化中的应用,通过基于Python开发的GPKit软件包提供的SP算法,对建立的电推进系统电气部件和机械部件的尺寸和性能参数化模型进行了优化,并通过分析对比涡轮直接驱动架构、涡轮-电驱动架构与变速涡轮-电驱动架构的总重与效率,说明了电推进系统在器件级优化设计中质量和效率之间的权衡。
本文针对目前电推进飞机顶层设计手段匮乏、能量流动与耦合机理不够明晰、关键部件的性能尺寸参数化模型缺乏积累的问题展开研究,以期为电推进飞机的设计与评估优化方法提供设计工具积累。
本文第1节介绍了潮流分析方法的基本概念,以及牛顿法的迭代计算流程,分析了电推进飞机电气系统在正常运行与断路故障情况下的电网状态与母线电压等级对电网的影响;第2节在SIMULINK环境下搭建了动力系统的仿真模型,同时设计了基于时间和基于高度的两种飞行剖面,给出了涡轮电推进与纯电推进架构的仿真分析结果;第3节建立了动力系统各部件的参数化优化模型,介绍了符号规划优化算法的基本原理,并利用该优化算法对动力系统进行了优化分析,得到了相应的分析结果;最后在第4节对全文进行总结,并给出了结论。
1 电推进飞机电气系统能流关系分析
潮流分析方法是一种获得电力系统各种电源及负荷在稳定状态下运行的参数的数值计算的方法。在电推进飞机系统中,发电机产生的电能是推进系统最主要的能量来源,对飞机电气系统使用潮流分析方法,可以得到固定运行状态下电网中的电压与电流分布情况,对电推进飞机电气系统的设计有着十分重要的意义。
1.1 潮流计算方法
1.1.1 数学模型
电力系统由发电机、负荷、输电线等部分组成,在进行潮流计算时,通常会将发动机与负荷这些非线性部件用接在对应节点上的电流量表示,而将其他的线性部件组合成用于潮流计算的线性网络。对于这种线性方程,一般采用节点法来得到节点电压与电流之间的关系,表达式为
(1)

对第i个节点,其展开式为

(2)
式中:n为电力网络总节点数。
通常在实际计算中,已知的数据为节点功率而非节点电流,因此,需要用节点功率来表示节点电流,得到节点功率与节点电压的表达式为
(3)
对节点电压向量用直角坐标形式可表示为
(4)
将导纳矩阵用复变量表示为
Yij=Gij+jBij
(5)
将节点电压向量的直角坐标表达式与导纳矩阵代入式(3)中,并按实部与虚部分开计算结果,就可以得到如下潮流方程:
(6)
该潮流方程通常也称为节点功率方程,是潮流算法最普遍采用的数学模型。
1.1.2 数值计算方法
用于潮流计算的数学模型是一组高阶的非线性方程,为了求解这些方程必然要用到迭代运算的方法。由于电网系统规模的不断扩大,用于潮流计算的方程组的阶数也越来越高,甚至会达到上万阶,人工解算这些方程组显然是不现实的,因此研究人员开始寻求利用数字计算机求解潮流问题。
最开始,受限于计算机内存与计算速度的限制,普遍采用的是以节点导纳矩阵为基础的高斯—赛德尔迭代法(导纳法)和以阻抗矩阵为基础的逐次代入法(阻抗法)[20]。导纳法的收敛性较差,而阻抗法虽然改善了迭代算法的收敛性,但每次迭代的计算量较大,无法满足大型系统的实时性要求。随着计算机的不断发展,牛顿—拉夫逊法(牛顿法)被广泛用于潮流计算问题中,牛顿法的核心是将非线性方程线性化,并反复地对相应的线性方程进行求解。在使用牛顿法时,只要保证初始值设置合理,同时在迭代过程中使方程组的系数矩阵保持其稀疏性,就能以很快的速率解决潮流计算的问题。由于牛顿法具有很好的收敛性与运行速率,牛顿法成为了处理潮流计算问题最主要的方法。
牛顿法是大部分电力系统潮流计算方法的基础,许多方法都是对其改进得到,因此,了解了牛顿法的迭代原理,对潮流计算问题也就有了相对透彻的了解。下面将简单介绍牛顿法的计算步骤,整个计算方法的流程如图1所示。
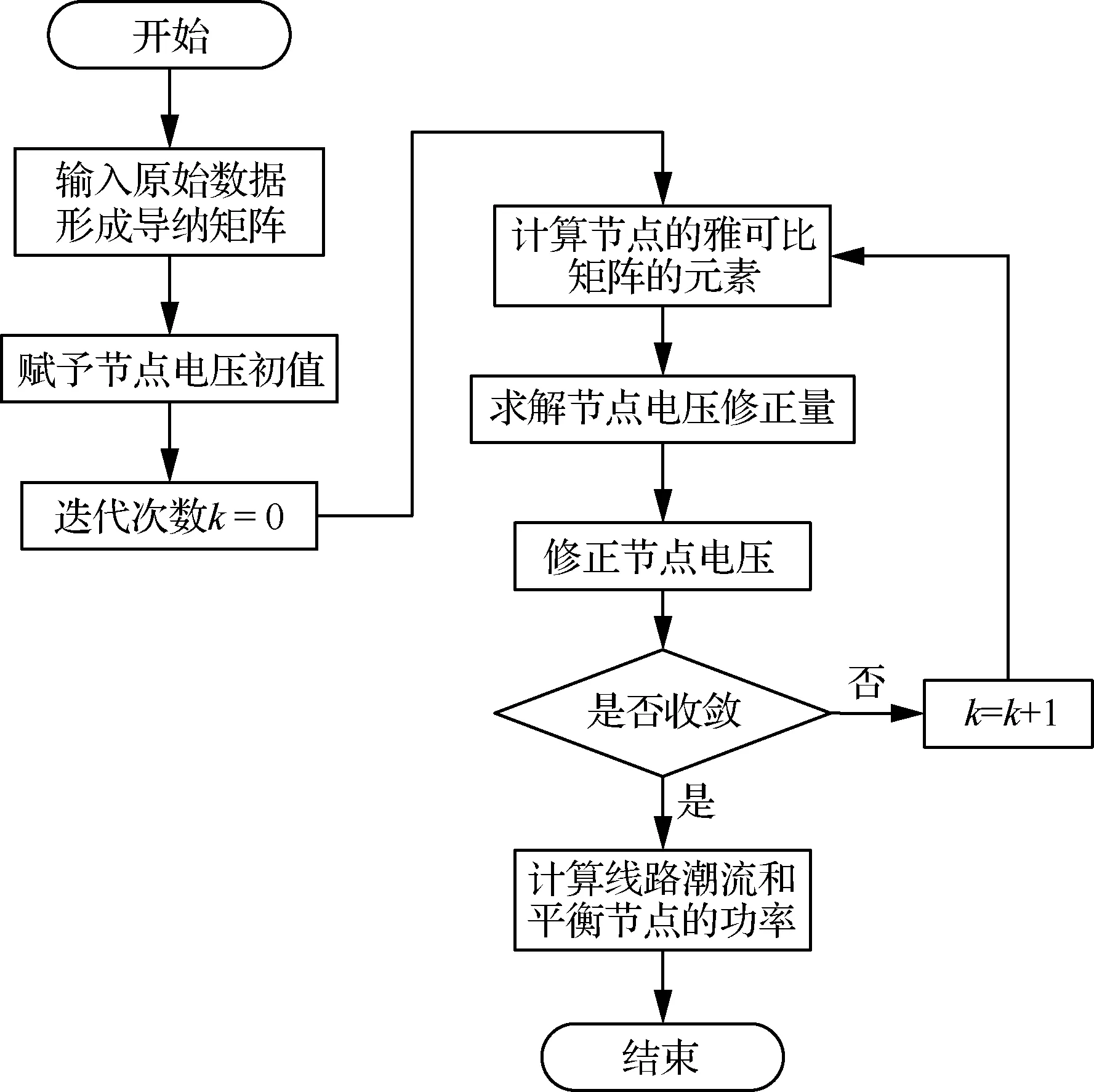
图1 牛顿法潮流计算流程图
1.2 潮流分析结果
1.2.1 配电架构选择
电推进飞机电气系统的能量传输架构多种多样,其中最常见的有直流电力系统、混合交直流系统和交流系统。对于直流系统架构,由于功率传输需要从变频交流发电系统,将电功率进行两次传输,在电机和电力电子变换器之间是交流电,在配电和传输系统之间为直流功率,因此电力系统包含了整流器和逆变器,存在功率损耗和系统重量之间的优化约束,但是由于发动机不提供系统推力,因此可以使其运行在最佳工作点,减小发动机的燃油消耗。交流架构在发电机和电动机之间没有电力电子变换器,因此功率损耗较小,但是其中需要将发动机输出功率传递到推进电机上,需要增加机械传动装置,不方便储能装置接入到电气系统中,也增加了系统对推力动态需求的不确定性。混合交直流系统中主要采用的是交流电,对应每一个电动机,采用背靠背变换器实现独立速度优化,但是多个电力电子变换器的使用,增加了系统的效率损耗。
由于直流输电系统能够保证发动机运行在最佳工作点,不需要额外的机械传动装置,同时减少电气系统的谐波污染与传输损耗,因此本文选择对这种配电体制进行潮流分析,并且对整个系统选择了分布式布局。采用这种设计方式的原因在于这种配电系统的潮流分析较为简单,可以将该分析结果作为基准数据,为后续的配电系统设计提供对比依据。系统构型如图2所示。
图2所示的电能传输系统是针对翼身融合分布式涡轮-电推进飞机系统设计的,系统共包括2个涡轮发电机系统与8个推进单元,整个配电系统共分为2组,每组各由1个发电机和4个推进单元组成。在该系统中,涡轮发动机与顶端的交流发电机相连,交流发电机产生三相交流电压传输到整流器,整流器将其转换为直流电压后,通过母线传输到逆变器,再由逆变器将直流电压转化为交流电压,驱动电动机工作,最终产生机械功率输送给推进器。
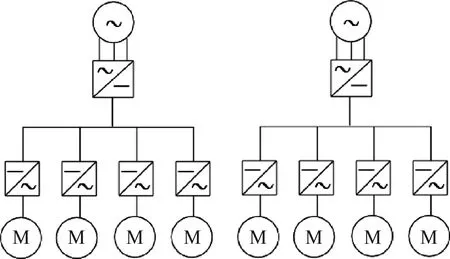
图2 分布式电推进飞机高压直流配电系统架构
由于两组配电系统是完全对称的,因此在接下来的分析中,只选取了其中一组进行分析。额定状态下4台电动机的有功与无功功率均设为相同,整流器与逆变器的参数统一用变换器表示,输电线每米的电阻值设置为0.009 6 Ω,配电系统具体的参数值设定如表1所示。

表1 配电系统额定状态参数值
1.2.2 稳定运行状态分析结果
考虑到飞机飞行过程中的姿态转换,稳定运行状态共分为2种情况。第1种是电动机负载功率对称分布,这种情况下飞机处于平飞状态;第2种是电动机负载功率从左到右等间距增加,这种情况下飞机处于倾转状态。为了便于进行对比分析,假设这两种情景下电动机负载提供的总功率不变,均为27.8 MW。出于系统安全冗余的考虑,推进部件中的逆变器母线之间通过输电线互相连接。流过直流输电线的电流以及直流母线电压的大小由不同颜色表示,具体的分析结果分别如下所述。
1) 电动机负载功率对称
在这种情况下,4台电动机负载的有功功率均设为6.95 MW,如图3所示,从分析结果中可以看出,由于中间位置的两根直流输电线的传输路径短,电阻较小,所以流过这两根输电线的电流是最大的,其中,绝大部分电流通过逆变器为电动机负载传输能量,小部分电流输送到了两侧的逆变器母线上。同时,由于电动机负载是对称分布的,因此没有电流流过连接中间2个逆变器的导线。

图3 负载对称稳定运行状态
在母线电压方面,直流母线2的电压与设定值相同,稳定在4 000 V,靠近中间的母线4与5的电压比两端的母线3与6的电压值稍微高出一些。
2) 电动机负载功率不对称
在这种情况下,4台发电机负载的功率按照0.1 MW的差值从左到右等间距增大,但电动机所提供的总功率仍然与负载功率对称情况下的数值保持一致。如图4所示,从分析结果中可以看出,直流输电线上的电流呈现出“中间大,两端小”的特点,虽然看上去直流输电线上流过的电流与负载功率对称情况下相同,实际上右侧输电线上的电流要比负载功率对称情况下略大一些,这是因为右侧的电动机负载的功率要比负载对称情况下更大。同时,有少量的电流流过了连接中间两个逆变器的输电线。在母线电压与发电机的有功功率方面,分析结果与电动机负载对称情况下相差很小,说明在负载功率相差不大的情况下,母线电压几乎没有波动,发电机所需提供的功率也没有改变。

图4 负载功率间距0.1 MW稳定运行状态
将负载功率的间距值增大到0.4 MW,如图5所示,从分析结果中可以看出,由于左侧电动机负载的功率变得更小,左侧直流输电线上的电流密度也随之进一步减小;同时冗余输电线的电流密度也呈现成同样的趋势,负载功率较小的一侧电流减小,较大的一侧电流增大。

图5 负载功率间距0.4 MW稳定运行状态
在母线电压方面,由于左侧直流输电线上的电流减小,母线3的电压有所上升,母线4的电压上升幅度很小,基本没有变化。值得注意的是发电机提供的有功功率发生了大幅度的下降,下降了0.21 MW,反映出负载功率不平衡运行状态有利于节约供电系统的能量损耗。
1.2.3 断路故障运行状态分析结果
在飞机运行过程中,除了分析稳定运行状态外,更重要的是分析系统发生故障时输电线的电流密度与直流母线电压的变化情况。本文选择了对直流输电线故障这一运行状态进行分析,考虑了单线断路与双线断路2种故障状态,并且保证电动机负载的总功率与负载对称稳定状态下相同。具体的分析结果如下所述。
1) 单线断路
如图6所示,断路的直流输电线被标为灰色。分析结果表明,由于存在输电线断路,没有发生故障的直流输电线上的电流都有不同程度的增大,并且与断路的输电线相邻的输电线电流增加幅度最大,这是因为原本应由断路的输电线提供的电流被分配到了该输电线上,同时连接中间两个逆变器的冗余输电线上流过了较大的电流,这说明该冗余输电线在故障情况下可以起到重新规划系统能流路径的作用。

图6 单线断路故障运行状态
从母线电压分析结果中可以看出,发生断路故障的母线3的电压有明显的下降,而其他直流母线电压的下降幅度没有这么大。由于断路故障使得整个配电系统的能流传输路径变长,发电机需要提供的有功功率与正常运行状态相比增大了0.025 MW。
可以看出,单线断路会引起配电系统其余输电线的电流密度增大,母线电压下降,同时发电机需要提供的总功率变大。
2) 双线故障
如图7所示,在左侧的两根直流输电线完全断路的情况下,与之距离最近的输电线上的电流大大增加,同时为了平衡系统的功率需求,最右侧的输电线电流也有所增加。
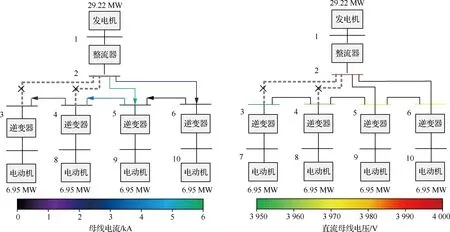
图7 双线断路故障运行状态
从母线电压分析结果可以明显看出,断路故障侧的直流母线电压相较于单线故障时下降了许多,同时另一侧的母线电压也有一定程度的下降。为了弥补系统能流路径加长带来的损耗,相比于稳定运行状态,发电机需要产生的有功功率增大到了29.22 MW,增加了约0.58%。
可以看出,双线故障的潮流分析结果与单线故障时的趋势相同,但变化的幅度更加明显。
通过以上分析,得到了飞机在采用分布式布局、高压直流供电体制时,配电系统在稳定运行状态与故障运行状态下的输电线电流密度,母线电压与发电机产生的功率大小,根据这些数据,可以为配电系统的输电线电流等级与变换器的选型提供理论依据,同时为不同工作状态下发动机轴功率需求变化提供理论数据。各种运行状态下各母线电压与输电线电流密度的具体值分别如表2与表3中所示。

表2 直流母线电压具体数据
1.2.4 直流母线电压等级对电网的影响
从表3的分析结果可以看出,负载平衡状态下电网中输电线的最大电流密度为2 432.15 A,在双线断路情况下最大电流密度值上升到了5 211.97 A, 电流密度越大,对输电线的载流量要求就越高,在同等长度下,输电线的质量也就越大。通常情况下,希望飞机电网中的最大电流不超过1 000 A,显然上述的分析结果已经远远超出了这一要求,这说明选取的母线电压等级不够合理,应当进一步提高直流母线的电压值。因此,对提高母线电压等级所带来的电网最大传输电流与发电机输出功率的变化进行了研究与分析。
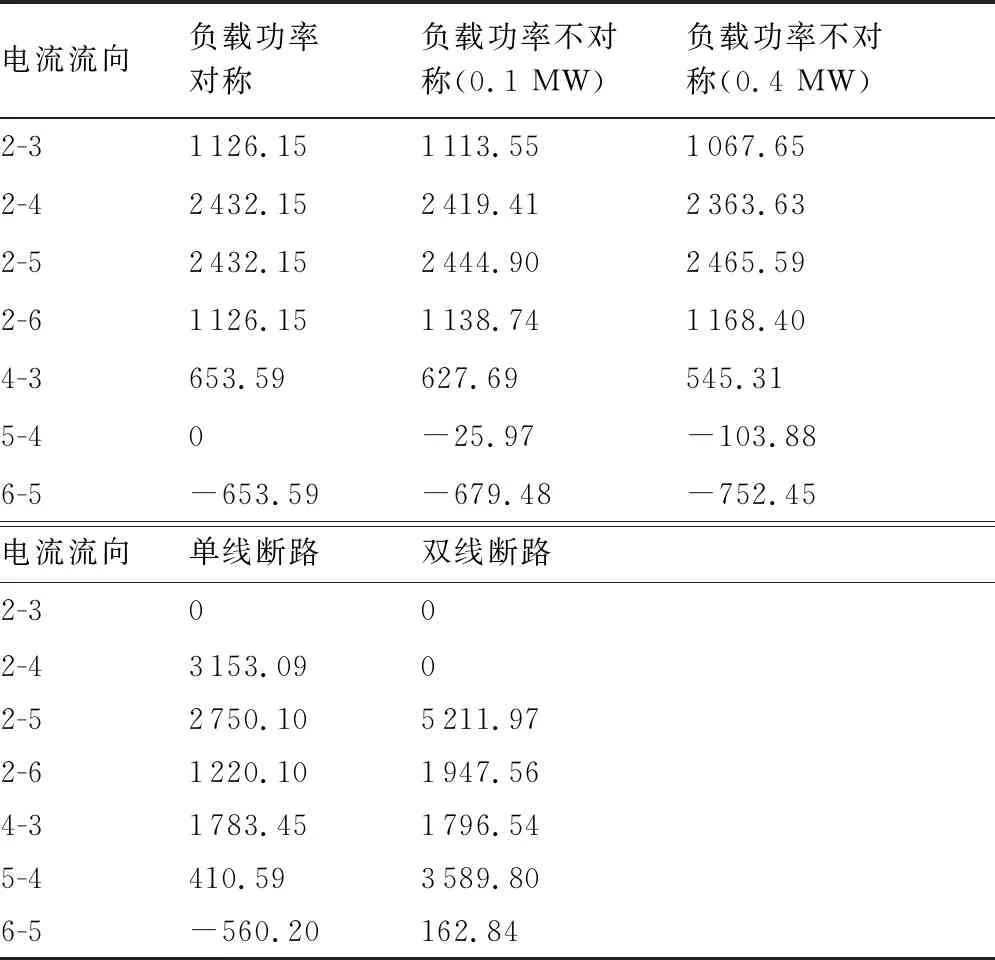
表3 直流输电线电流密度具体数据
由于负载功率平衡情况与双线断路情况下输电线的电流密度与发电机的输出功率在所有情景下处于最大值,因此选择了这两种情况进行分析,分析结果如图8与图9所示。

图8 输电线最大电流密度随母线电压变化关系

图9 发电机输出功率随母线电压变化关系
可以看出,随着母线电压等级的升高,输电线的最大电流密度以及发电机输出功率都在下降,并且曲线逐渐变得平滑,说明在母线电压等级到达一定数值后,继续增大对电网的影响将变小。在母线电压升高到10 000 V时,输电线电流密度下降到了1 000 A以下,此时双线断路故障情况下的最大电流也仅有2 067 A,继续增大母线电压,虽然电流密度与发电机功率可以进一步减小,但过高的电压会降低飞机电气系统的安全性,综合各种因素考虑,对于该电气系统,直流母线电压选择在9 000~10 000 V之间最为合适。
2 动力系统仿真模型
在第一部分中,对分布式电推进飞机电气系统的能量流动情况进行了研究,但是,完整的电推进飞机动力系统不仅包括电气系统,还包括了推进系统,只有将推进系统产生的推进功率与电动机的电功率相耦合,得到的电气系统的功率分布情况才是有意义的。由于第1章中研究的动力系统总的推进功率较大,给系统各部件具体参数的设置带来了一些困难,因此本章在SIMULINK环境下,针对某小型电推进飞机混合动力系统,分别搭建了其纯电推进架构和涡轮-电推进架构仿真模型,并对其电气系统的性能进行了相应分析。
2.1 混合动力系统组成
本文分析了纯电推进和混合动力推进2种架构,2种架构的主要区别在于纯电推进架构仅由储能装置提供能量,而涡轮-电推进架构是由发电机与储能系统共同提供能量。从图10中可以看出,电推进飞机动力系统主要由供电系统、储能系统与推进系统3部分组成。
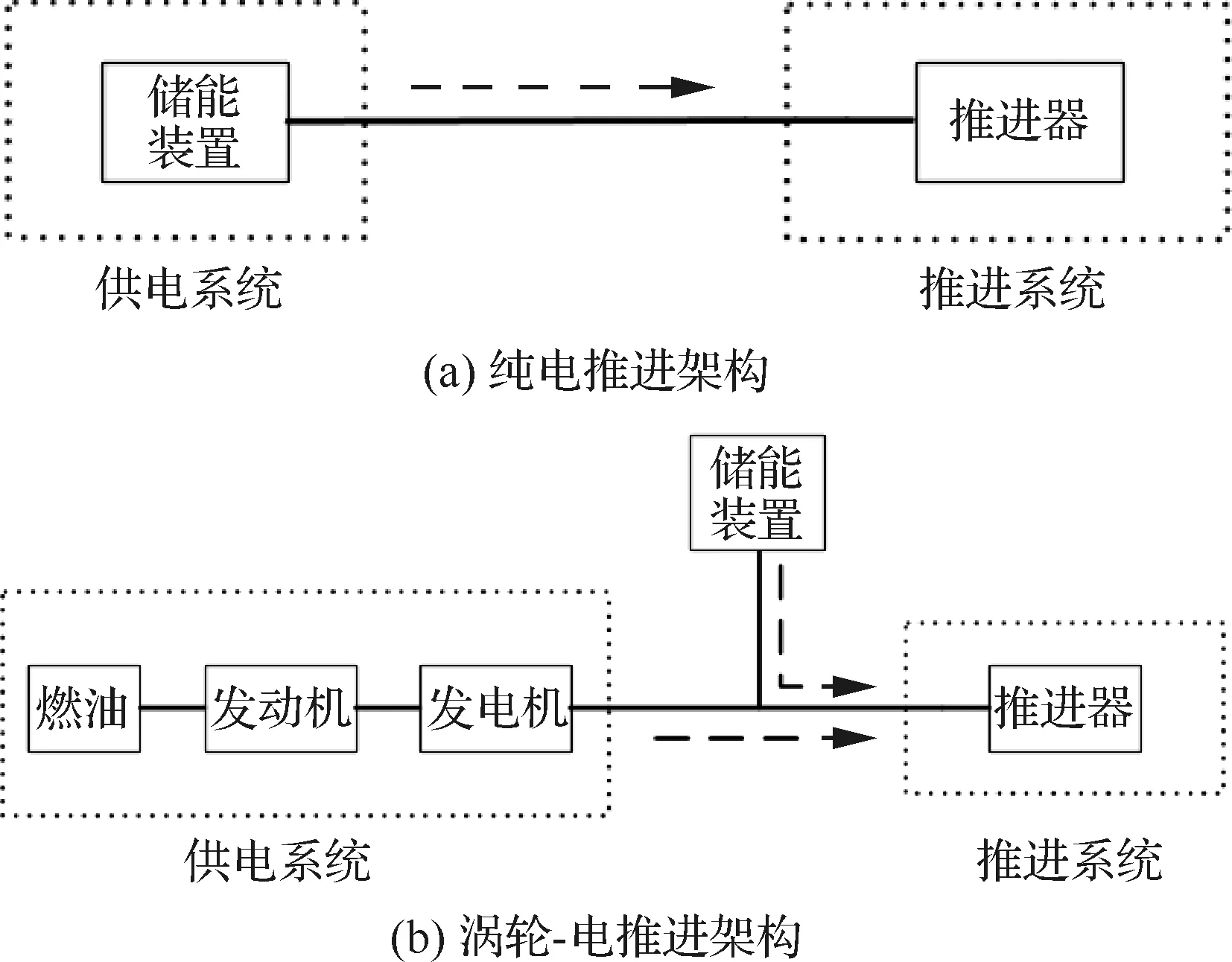
图10 混合动力系统架构
2.2 仿真模型搭建
模型被划分为飞行控制信号模型、飞机的气动模型、配电系统模型、储能系统模型与涡轮发电系统模型,具体使用到的组件包括发动机、发电机、整流器、锂电池组、DC-DC变换器与电动机,模型中共有4台推进器,并认为飞机推力被平均分配到4台推进器上,整体仿真模型如图11所示。进行仿真的目的在于分析动力系统的能量流动与功率分配关系,因此所选用的模型都是系统级参数化模型。

图11 涡轮-电架构仿真模型
由于纯电推进系统架构与涡轮-电推进系统架构相比,仅仅不包含涡轮发电系统,因此纯电推进系统的仿真模型图在此处不再给出。
在电推进动力系统的设计阶段进行仿真实验时,通常会采用后向仿真计算方法来实施系统仿真。所谓后向计算方法是指在已知系统运行状态的条件下,根据运行状态从后向前计算出系统处于稳定运行状态时能流路径上每一个部件的功率需求,采用这种仿真方法的优势在于能够计算出系统在给定工况下全部部件的运行状态,为系统的方案设计与部件选取提供重要的参考信息。
在这种仿真方法中,需要已知飞机的飞行剖面。在本文中分别设计了基于时间与基于高度的两种飞行剖面。
2.2.1 基于时间的飞行剖面
如图12所示,基于时间的飞行剖面共包括5个阶段,依次为滑跑—起飞—爬升—巡航—下降,通过定义飞机在每个飞行阶段的航迹角与迎角,可以计算得到具体的推力需求,以及飞机的需求推进功率,将需求功率作为配电模型的输入量,就可以实现推进系统与电气系统的耦合。

图12 基于时间的飞行剖面
2.2.2 基于高度的飞行剖面
采用基于时间的飞行剖面有利于分析飞机动力系统在每个飞行阶段以及过渡阶段的能量流动情况,但这种设计方式的缺点在于不能充分反映飞机实际的工作状态。在实际情况中,飞机通常会在达到预定的高度后进入巡航状态,在能量将要耗尽时返航。为了分析这种情况中涡轮-电推进与纯电推进架构航程的差异,设计了基于高度的飞行剖面,如图13所示。此时,飞机不再包括下降阶段,在飞行高度达到300 m时进入巡航状态,在电池的荷电状态(SOC)下降到35%时,仿真停止。

图13 基于高度的飞行剖面
2.2.3 推进系统推力计算
为了实现电推进飞机动力系统的完整仿真,需要计算出推进系统的输出机械功率,从而建立其与供电系统输出电能的耦合关系。因此下面将具体分析飞机的气动模型,推导飞机的空气动力计算数学公式。
图14为飞机受力分析示意图,其中L表示飞机机翼产生的升力,D表示机体受到的阻力,T表示推进器提供给飞机的推力,方向与机翼弦线方向一致;α为飞机的迎角,指速度方向与机翼弦线之间的夹角,飞机飞行时机翼上的空气动力与迎角有关;γ为航迹角,是飞机相对地面的运动方向夹角。

图14 飞机受力分析示意图
机翼产生升力的大小可以用如下式(7)表示,计算物体的阻力大小所采用的公式与计算升力的方法相似[21]。
(7)
(8)
式中:ρ为当前飞行高度下的空气密度;V为飞机与气流的相对速度(飞行速度);Sw为翼展面积;CL与CD分别为升力系数与阻力系数。
将飞机的受力情况按照飞行速度方向进行分解,分别在速度方向及其垂直方向上可以得到如下受力平衡公式:
Tsinα+L=mgcosγ
(9)
Tcosα-D-mgsinγ=ma
(10)
只要得到了飞机的航迹角γ与迎角α,就可以根据式(9)计算出推力器提供的推力大小,在得到推力的值后,代入式(10)中,可以计算出飞机的加速度,再经过积分后,就可以算出飞机的飞行速度。有了这两个物理量,推进器的机械功率便顺势得出,再根据推进器的效率曲线就能够计算出供电系统所需提供的电功率。这样,就实现了飞机推进系统与电气系统的能量耦合。
2.3 仿真分析结果
采用基于时间的飞行剖面时仿真模型中各部件的主要参数设置的具体值如表4所示。

表4 仿真模型参数设置
2.3.1 推进功率与效率仿真结果
首先根据基于时间的飞行剖面对系统进行仿真,对比2种架构在不同飞行阶段推进功率与效率的变化情况。
从图15和图16可以看出,涡轮-电推进架构下飞机的推进功率在全过程中都是大于纯电推进架构的,并且呈现出相同的变化趋势。在地面滑跑阶段,推进功率线性增大,进入起飞与爬升阶段后,由于迎角增大,飞机产生的推力大幅度减小,推进功率也随之下降;在巡航阶段,推进功率略有减小,与爬升阶段基本相同;在最后的下降阶段,由于飞机的重力势能转化为动能,不再需要推进器提供大部分能量,因此推进功率大幅下降。
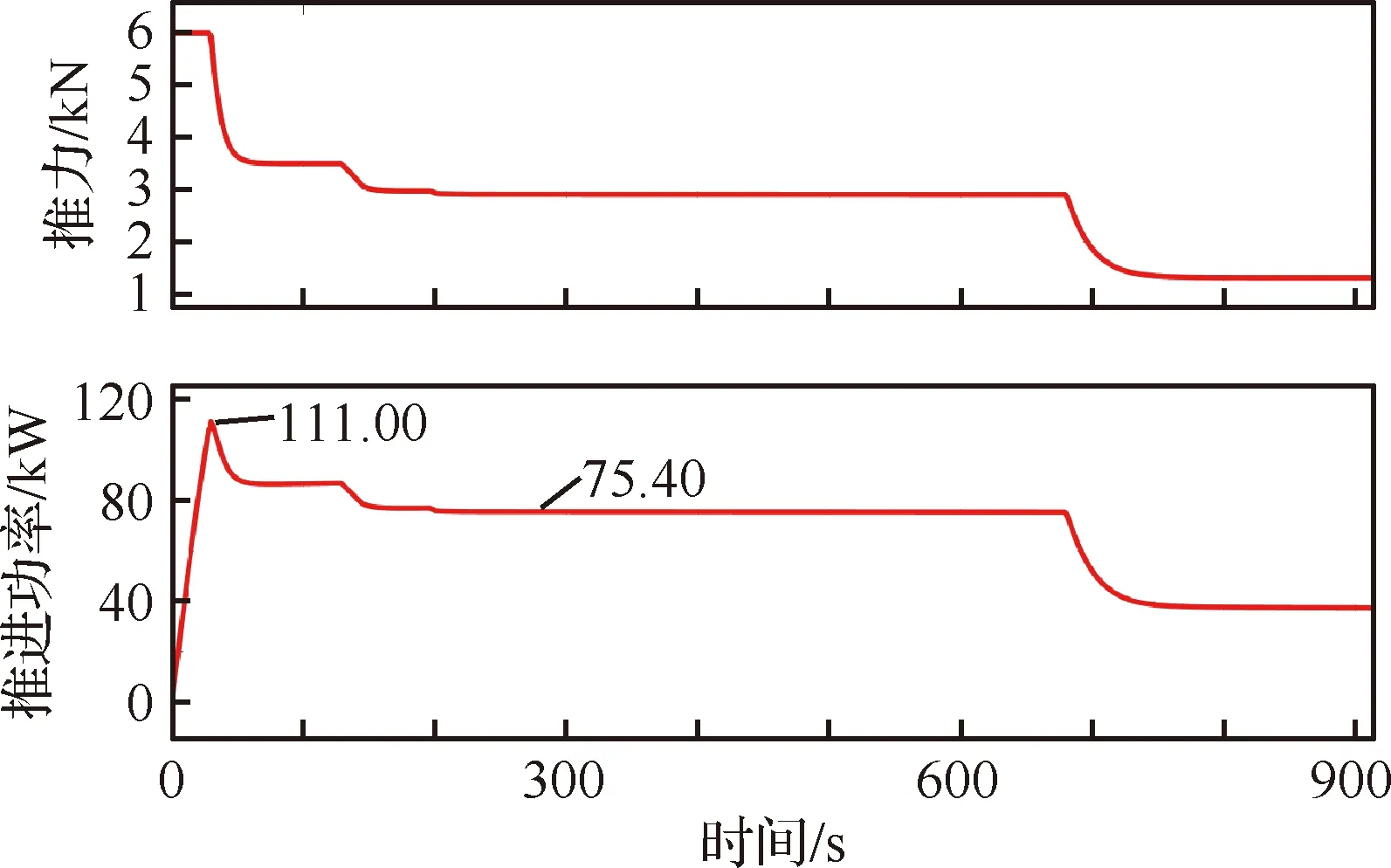
图15 涡轮-电推进架构推力与推进功率曲线

图16 纯电推进架构推力与推进功率曲线
飞机的推进效率曲线与推进功率的变化趋势相同,随着推进功率的下降而下降,同时纯电推进架构的推进效率在全飞行过程中都是高于涡轮-电推进架构的,这是因为涡轮-电架构中含有效率较低的发动机部件。
2.3.2 供电系统功率分配仿真结果
从图17可以看出,涡轮-电推进架构中,电动机的输入电动率等于发电机与电池的输出电功率之和。在地面滑跑阶段,电动机的电功率需求从零开始不断增大,在小于发电机的输出电功率时,发电机为电池充电,在超过发电机电功率后,电池开始放电,在巡航阶段,发电机的输出功率与电动机输入电功率基本持平,电池只需要提供4.92 kW的功率;在下降阶段,电动机功率需求降低,电池再次进入充电状态,充电功率为38.20 kW。由于纯电推进架构中,电池提供了动力系统全部的能量,因此电池的功率变化趋势与电动机的功率需求变化相同。
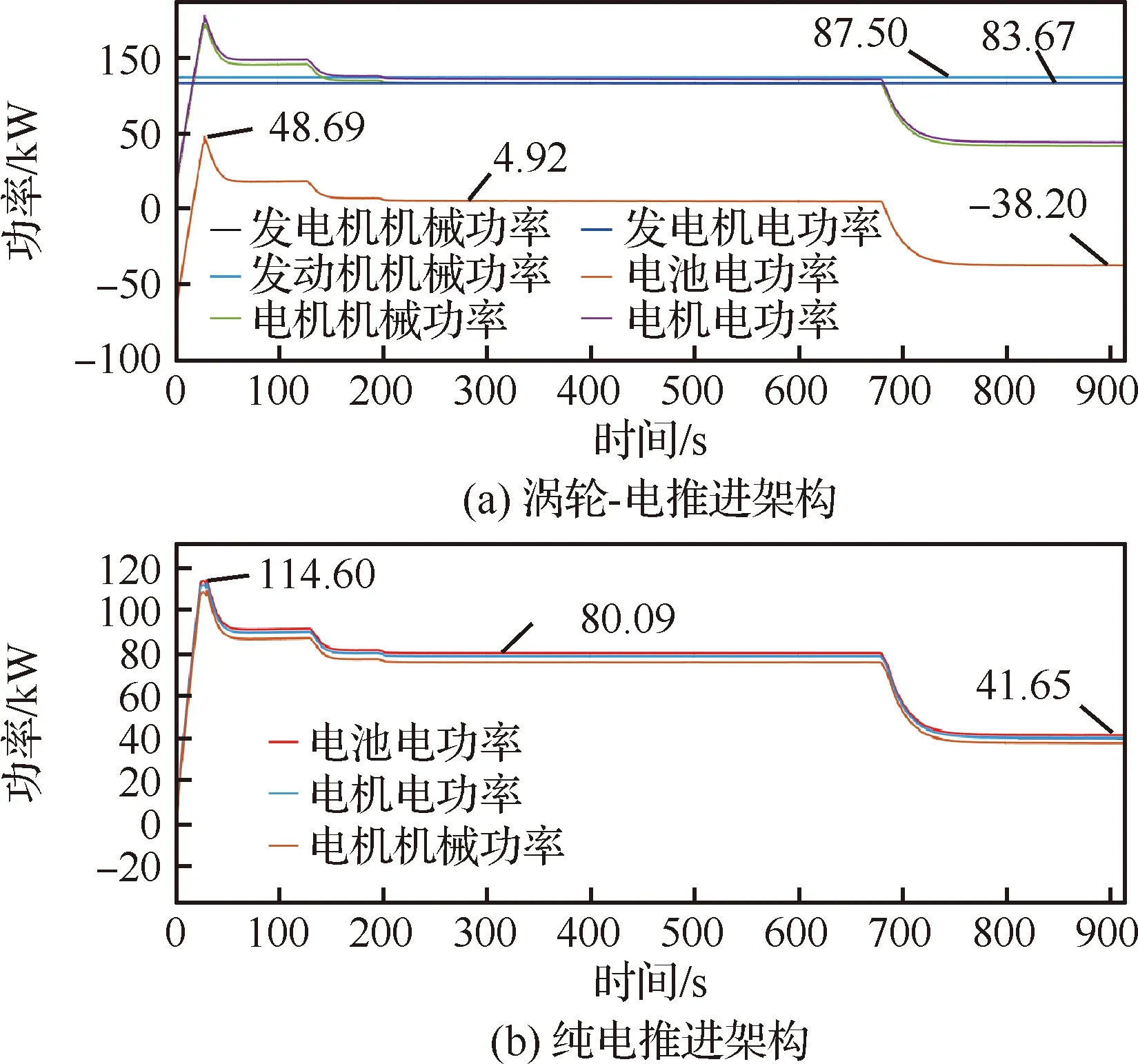
图17 供电系统各部件功率曲线
由于两种架构下电池的工作状态完全不同,因此有必要在两种架构下对电池的充放电曲线进行对比分析。
从图18可以看出,在涡轮-电推进架构中,电池的SOC值最大下降到91.77%,在进入下降阶段后,经过发电机充电,最终达到97.12%,而电池的SOC初始值为95%,全程消耗的燃油量为6.352 kg,经过整个飞行过程电池的电量是增加的,应当继续优化系统的相关参数,使电池充放电平衡;在纯电推进架构中,电池一直处于放电状态,SOC最终下降到42.52%。同时,涡轮-电推进架构电池的最大充放电电流约为纯电推进架构的58%,电池的过电流较小,系统更加安全。
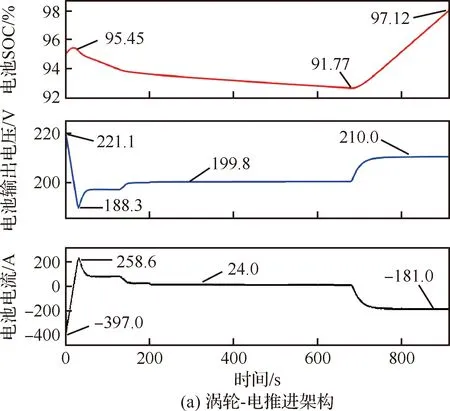
图18 电池充放电曲线
2.3.3 供电系统功率分配仿真结果
在基于时间的飞行剖面下,飞机经历了完整的飞行过程,比较2种架构下的航程没有太大的意义。因此,采用基于高度的飞行剖面分析了航程与电池容量和任务载荷的关系。由于基于时间的飞行剖面中发动机的输出功率较大,导致电池组的能量没有得到充分的利用,因此将发动机的功率设置为70 kW,重新进行了仿真。
从图19可以看出,航程随电池容量的增大而增加,但由于飞机的总重也增加了,因此随着电池容量的增大,航程的增加速率逐渐变慢。同时,对比2种架构可以发现,电池容量越大,两者航程的差值越大,这说明在仅增大电池容量的情况下,涡轮-电推进架构有更好的效果。从图20看出在电池容量恒定时,随着任务载荷的增大,飞机的航程一直在减小,并且涡轮-电推进架构的下降速率明显要高于纯电推进架构,说明涡轮-电推进架构受飞机总重增加的影响更大。

图19 航程随电池容量的变化关系图
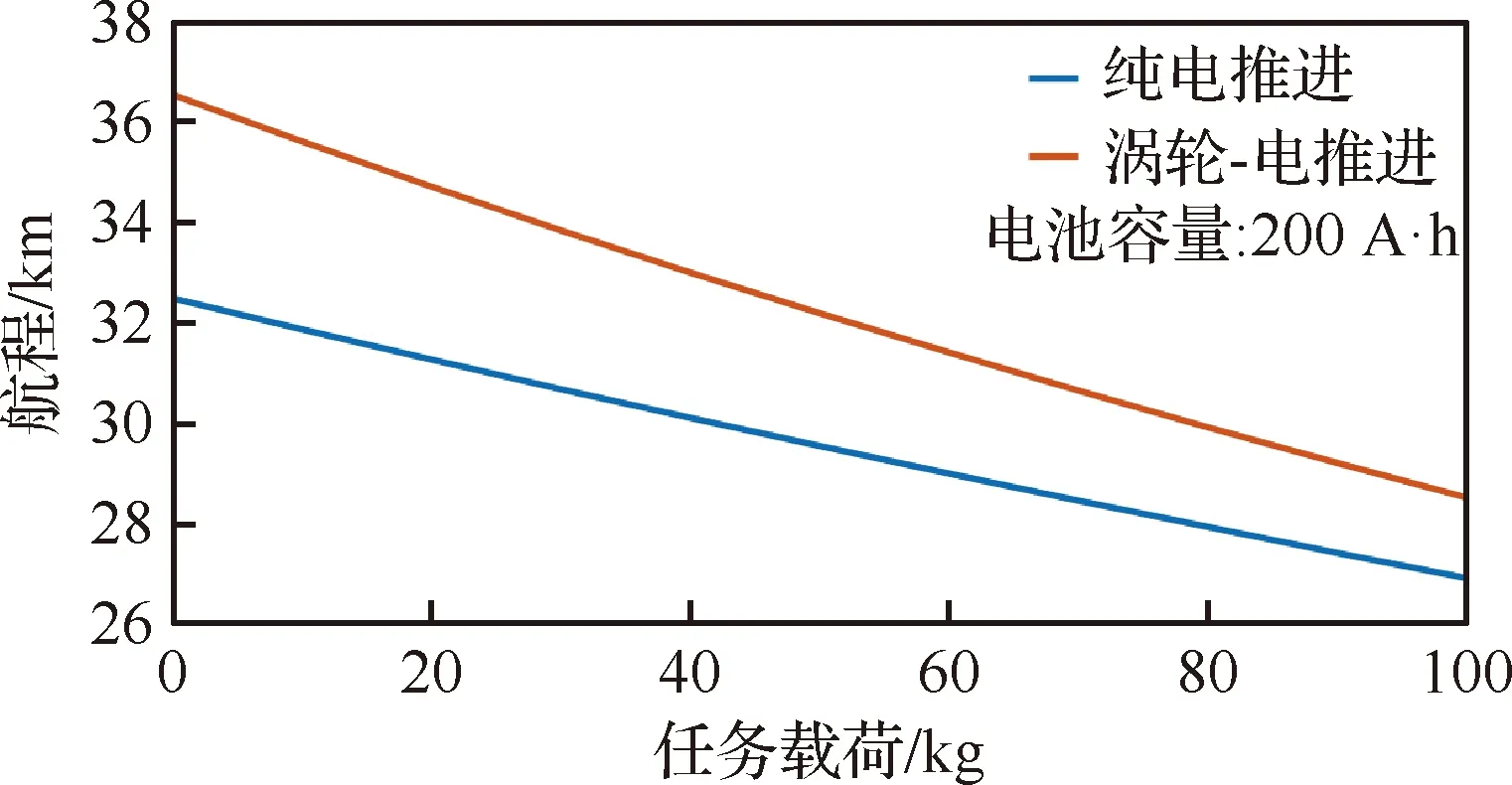
图20 航程随任务载荷的变化
由上面的分析可以发现,电池容量增大与任务载荷增大对两种架构航程的影响是相反的,为综合考虑两种因素对飞机航程的影响,进一步绘制了电池容量、任务载荷与航程的三维关系图。
从图21中可以明显看出,涡轮-电推进架构可以在更小的电池容量等级下达到选择的航程临界值,并且能够承载更多的任务载荷,在航程方面是完全优于纯电推进架构的。

图21 航程与任务载荷及电池容量的三维关系图
3 动力系统参数化建模与优化
在第2部分中,搭建了动力系统完整的仿真模型,并对比分析了纯电推进与涡轮-电推进架构的优劣。模型相关参数的设置是根据假定的功率重量比通过估算得到的,所建立的仿真模型精细度不高,为了解决这一问题,本部分建立了输电线与电机的参数化模型,并利用符号规划算法分别对其进行了优化分析,同时分析了传统涡轮推进和涡轮电推进架构的动力系统总重与燃料消耗率之间的权衡关系。
3.1 符号规划优化算法
符号规划(SP)算法是几何规划(GP)优化算法的一种更通用的表示算法。几何规划算法主要用于解决具有非线性目标和约束条件的优化问题,由于其利用了拉格朗日对偶原理,因此可以把高度非线性方程转化为具有线性约束的方程求解,同时可以确保全局最优解,为解决多学科飞机设计优化问题提供了独特而强大的方法,因此目前已经被应用于飞机气动模型的设计优化[22-23]。但是,并非所有飞机的设计约束都能够满足GP算法的约束条件,因此考虑通过减小设计约束来解决这一问题,即采用更一般化的SP算法。
在介绍符号规划算法之前,首先对几何规划算法作简单介绍,并简要说明其优势和局限性。
对于GP算法,只要存在可行的解决方案,求解器无需要求初始猜测值与实际的准确值接近就可以保证收敛到全局最优。
在GP算法中,目标函数和约束条件只能由单项式和多项式函数组成,其形式分别为
(11)
(12)
式中:aj为任意实数;ak、c、ck、uj为正实数。
简单来说,GP算法受单项式等式约束和多项式不等式约束的约束,最小化了多项式目标函数,用数学语言描述GP算法如下:
minimizep0(u)
subject topi(u)≤1,i=1,2,…,np
mi(u)=1,i=1,2,…,nm
(13)
相比于GP算法,SP算法的最大优势在于可以将ck的取值范围扩展到全体实数,从而解决GP算法设计约束中常量系数不能取负的问题。但是SP算法中的目标函数不是凸函数,不能保证全局最优解,因此需要通过将GP算法中的函数形式转换到对数空间中以将其转化为凸优化问题。
经过代换,得到几何规划算法的数学描述为
(14)
式中:T表示连乘符号。
对式(14)取对数,目标函数与不等式约束函数将转化为凸函数,等式约束函数是仿射函数,SP算法被转化为凸优化问题。
本文利用了基于Python的GPkit[24]软件包提供的SP算法,对建立的参数化模型进行优化分析,该软件专门用于处理多学科领域的复杂优化问题。
3.2 关键部件参数化模型
3.2.1 输电线参数化模型
假设输电线由内导体层与外绝缘层组成,绝缘层的厚度要求能够防止电介质击穿,导体层的尺寸根据输电线的最大传输电流决定。如图22所示,输电线截面中导体层半径为a,外绝缘层的半径为b。导体层采用绞合线以减轻由交流信号引起的趋肤效应与邻近效应,可以看出,绞合线之间存在空隙,因此在导体层中有效导电面积并不能覆盖整个导体层,设其占整个导体层的比例系数为kpf。

图22 输电线横截面示意图
根据横截面,可以求出输电线的有效导电面积Ac与外绝缘层横截面积Adi分别为
Ac=πa2kpf
(15)
Adi=π(b2-a2)=π(b+a)tdi
(16)
式中:tdi=b-a表示绝缘层的厚度。
当输电线绝缘层中的电场超过最大电场强度Emax时,绝缘层中的电介质会被击穿,引起漏电。假设电介质的厚度非常小,电场强度的计算采用平行板近似,得到最大电场强度为
(17)
显然,在输电线的电压一定时,对输电线的厚度有最小值的限制要求。
假设输电线的长度为lc,导体密度为dc,绝缘体密度为ddi,结合式(15)与式(16),可以求出输电线的质量为
mc=Aclcdc+Adilcddi
(18)
在计算输电线传输效率时,将其当作电路中的恒定电阻处理,根据式(19)所示的输电线电阻表达式与假定的输出功率Pout,就能够得到输电线的效率表达式。
(19)
(20)
式中:ρc为导体材料电阻率。
选择输电线导体层半径a与绝缘层厚度tdi作为设计变量,约束条件为式(17),目标函数为式(18),将其取最小值,使输电线的总质量为最小。
3.2.2 电机参数化模型
电机的种类多种多样,由于齿槽式永磁同步电机产生的转矩大,效率高,在航空领域十分常见,因此在本文中选择对该种电机进行建模。假设该电机为三相电机,并且每极中有3个齿槽。永磁同步电机通常由5部分组成,如图23所示,分别为定子铁芯、定子齿、绕组、永磁铁和转子铁芯[25]。由于每一部分的几何形状不同,对其质量的计算方法也有所不同,下面将分别介绍各部件质量的建模方法[19]。
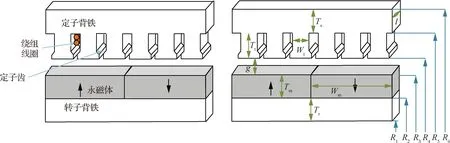
图23 永磁同步电机结构示意图
定子铁芯与转子铁芯具有相同的圆柱形几何形状,因此两者的质量计算公式类似。
转子铁芯的质量计算公式为
π(R2+R1)Trldrotor
(21)
式中:R1、R2为转子铁芯的内半径与外半径;Tr=R2-R1为转子铁芯的厚度;drotor为转子材料的密度;Arbi为转子铁芯的面积。
定子铁芯的质量计算公式为
π(R6+R5)Tsldstator
(22)
式中:R5、R6为定子铁芯的内半径与外半径;Ts=R6-R5为定子铁芯的厚度。
永磁体也可以看作圆柱体形状,其质量计算公式与定子铁芯相似,为
π(R3+R2)Tmldmag
(23)
式中:R3为永磁体的外半径;Tm=R3-R2为永磁铁的厚度。
假设单个定子齿的截面是厚度为Tt,宽度为Wt的矩形,电机中定子齿的总个数为6p,那么定子齿占据的总截面积Ateeth为
Ateeth=6pTtWt
(24)
假设定子材料的密度为dstator,可以得到定子齿的总质量为
mteeth=Ateethldstator
(25)
绕组线圈缠绕在定子齿上,定子齿与凹槽共同组合成的几何体的内半径为R4,外半径为R5,且有定子齿厚度Tt=R5-R4,可以得到定子齿与凹槽的面积之和为
π(R5+R4)Tt
(26)
假设绕组线圈占定子凹槽的比例为kpf,线圈材料的密度为dcond,则凹槽中的绕组质量为
mwind,in=kpfAslotsldcond
(27)
除凹槽中的绕组外,还有一部分绕组缠绕在电机外部,将这部分绕组成为称为端部绕组。假设端部绕组为三角形形状,端部绕组末端的斜边长度可以表示为[26]
(28)
式中:λ表示定子凹槽占定子总面积的比例。
综合考虑两部分绕组,可以得到绕组的总质量为
mwind=kpfAslots(l+2Let)dcond
(29)
电机的总质量为各部件的质量之和,如式(30)所示:
mmotor=msbi+mteeth+mwind+mmag+mrbi
(30)
电机的功率损耗主要包括欧姆热损耗、涡流损耗与磁滞损耗,从输入功率中减去以上损耗后,就可以得到电机的输出功率,进而计算出电机的效率。
假设电机模型为交流三相电机,相电阻为总电阻的1/3,电流流过的截面积只考虑定子凹槽的部分,电机模型的电阻表示为
(31)
进而求出电机的欧姆热损耗为
Pohmic=I2(2Rph)
(32)
涡流损耗Peddy与磁滞损耗Physt分别根据经验公式计算得到[27]
(33)
(34)
式中:ke、kh分别表示涡流损耗系数与磁滞损耗系数;α1为指数拟合系数;f为主电源频率;Bteeth为定子齿的磁通密度。
可以看出,这两种损耗与定子齿和永磁铁的质量,以及电机的旋转角速度和极对数有关,并且随着转速的升高而增大。
电机的效率表示为
(35)
选择转子铁芯的内半径R1、厚度Tr,定子铁芯的内半径R5、厚度Ts,永磁体的厚度Tm,定子齿的厚度Tt,绕组线圈占定子凹槽的比例kpf,电机的轴长l等参数作为设计变量,约束条件为电机各部分的磁通密度小于其对应材料的饱和磁通密度,如式(36)~式(39)所示,最终目标函数为式(30),将其取最小值,使电机模型总重最小。
(36)
(37)
(38)
(39)
式中:Brbi为转子铁芯的磁通密度;Bsbi为定子铁芯的磁通密度;Bsat为定转子材料的饱和磁通密度;Bgap为气隙平均磁通密度;μ0为真空磁导率;M为磁化常数;g为气隙厚度;Jm为电机的最大电流密度。
3.3 参数化模型优化结果
3.3.1 输电线模型优化结果
从输电线的效率表达式可以看出,在输电线的输出功率一定时,通过减小输电线的电阻值或输电线流过的电流值来提高效率,同时输电线的电阻与导体材料的电阻率ρc和输电线的长度lc成正比,与有效导电面积Ac成反比,在飞机的结构确定后,一般导体材料与输电线长度不会再有变化,因此输电线的电阻仅和有效导电面积Ac有关,增大有效导电面积可以减小输电线的电阻值,提高输电线效率,但同时会增加输电线的重量。另一方面,通过提高输电线的电压等级可以减小输电线电流,但同时会增大输电线的绝缘层厚度,导致输电线重量的增加。
综上所述,输电线效率的提高是以重量增加为代价的,同时与输电线的电压等级有很大关系。因此,利用优化算法得到了在不同电压等级下,输电线达到给定效率值的最小质量。
从图24可以看出,随着电压等级的升高,在效率不变的情况下输电线的质量逐渐减小,当电压升高至300 V时,输电线的质量基本不再发生较大的变化。同时,在同一电压等级下,输电线的质量随着效率的增大而增加,在效率较小时,质量的增加速度并不是很大,但是在效率值达到99.5%之后,每提升0.1%输电线的质量就会急剧增加,显然,过分追求输电线的高效率对于整个动力系统来说是得不偿失的。
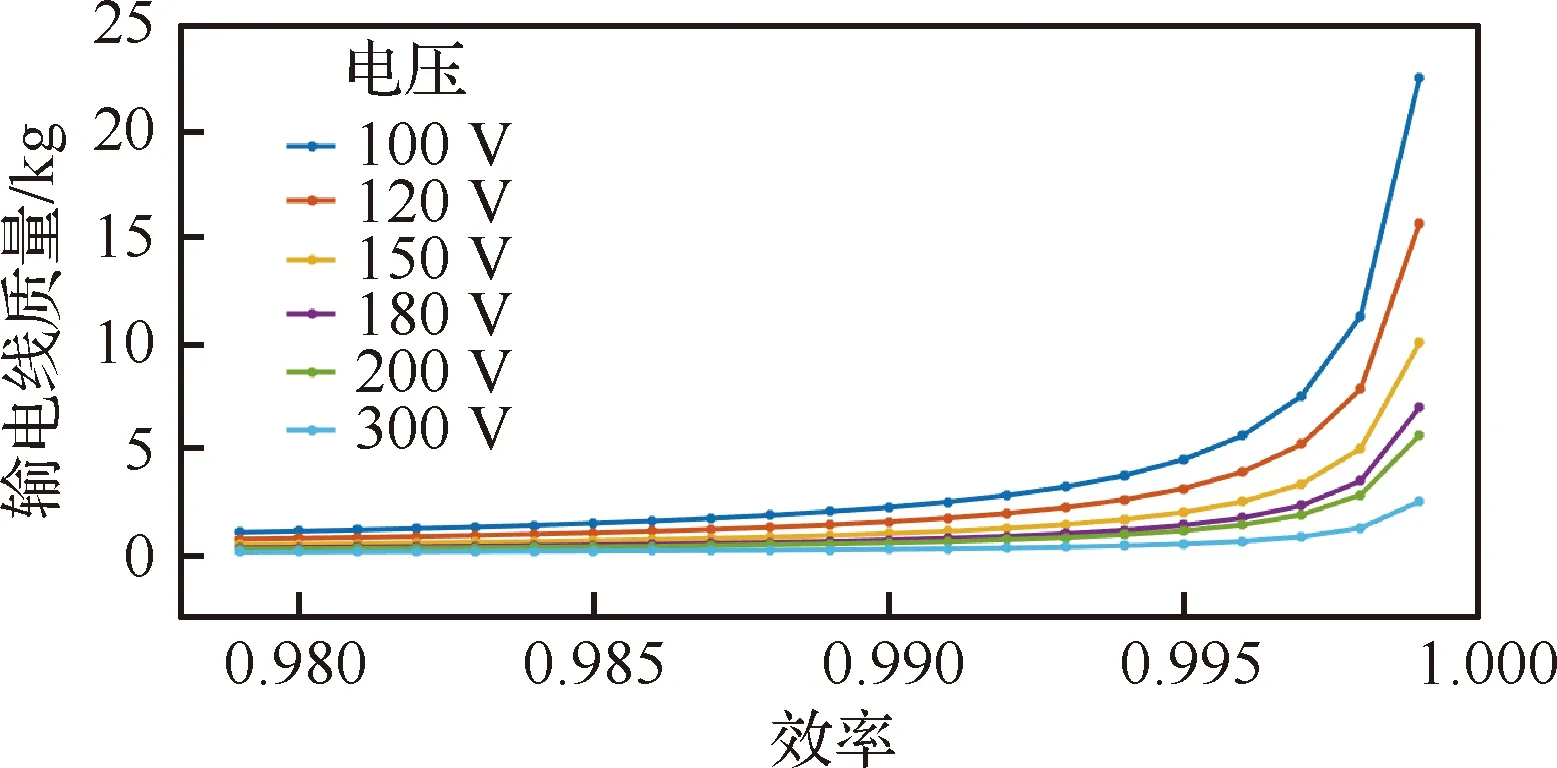
图24 不同电压等级下输电线效率与质量的关系
3.3.2 电机模型优化结果
电机模型的优化分析结果会受到多种参数的影响[28],在本文中选择电机的转速作为变量,以电机总质量最小为优化目标,利用优化算法,得到了电机质量与效率随角速度的变化关系。
如图25可以看出,随着转速的不断上升,电机模型的总质量一直减小,而效率在短暂增大之后也一直减小。这是因为在输入机械功率不变的情况下,角速度增大会导致发电机轴长、永磁铁外径、气隙磁通密度、绕组线圈面积4种变量的同时或单个数值减小,继而导致发电机总质量的减小。另一方面,最开始阶段效率的增加是因为绕组线圈面积有所减小,导致线圈中流过的电流减小,欧姆热损耗减小,此时由于角速度不大,涡流损耗与磁滞损耗占总功率损耗的比例较小,随着角速度的不断增大,这2种损耗在总损耗中占据了主要部分,导致发电机的效率降低。
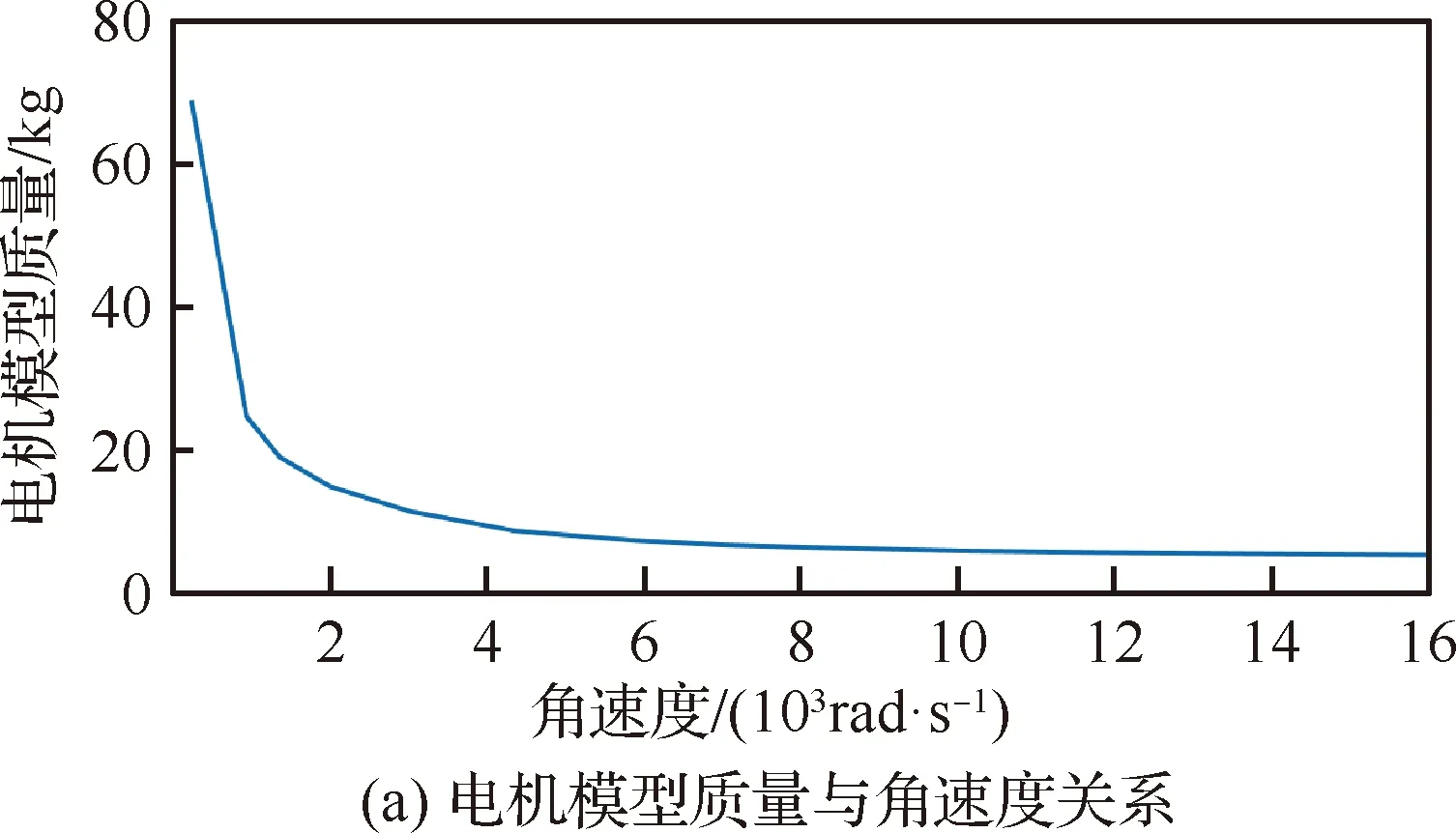
图25 电机模型质量与效率随角速度变化关系
3.4 动力系统整体模型优化结果
对输电线与电机模型的优化分析可以看出,输电线与电机的效率越高,其质量也会越高。为了获得动力系统整体质量与效率之间的权衡关系,从燃料消耗率与动力系统总重两个尺度对常规的涡轮推进架构与涡轮电推进架构进行了比较。
在涡轮推进架构中,涡轮风扇发动机直接与推进器涵道风扇连接;而涡轮电推进架构中,涡轮发动机驱动发电机转动,产生的电能通过输电线传输到电动机,再驱动涵道风扇产生推力。2种架构的具体配置方式如图26所示。

图26 推进系统架构示意图
对两种架构的系统总质量与油耗率之间关系的分析结果如图27所示。
由图27可以看出,在只有单台涵道风扇的情况下,传统的涡轮发动机推进架构相比于涡轮电推进架构更为轻便,推进效率也更高,并且动力系统总质量越小,涡轮发动机推进架构的效率优势愈发明显。这说明,如果不增加涵道风扇的数量,不考虑分布式布局下动力系统在气体动力学上的效率提升,使用发电机和电动机将涡轮发动机和涵道风扇的机械功率进行解耦没有系统级的收益。
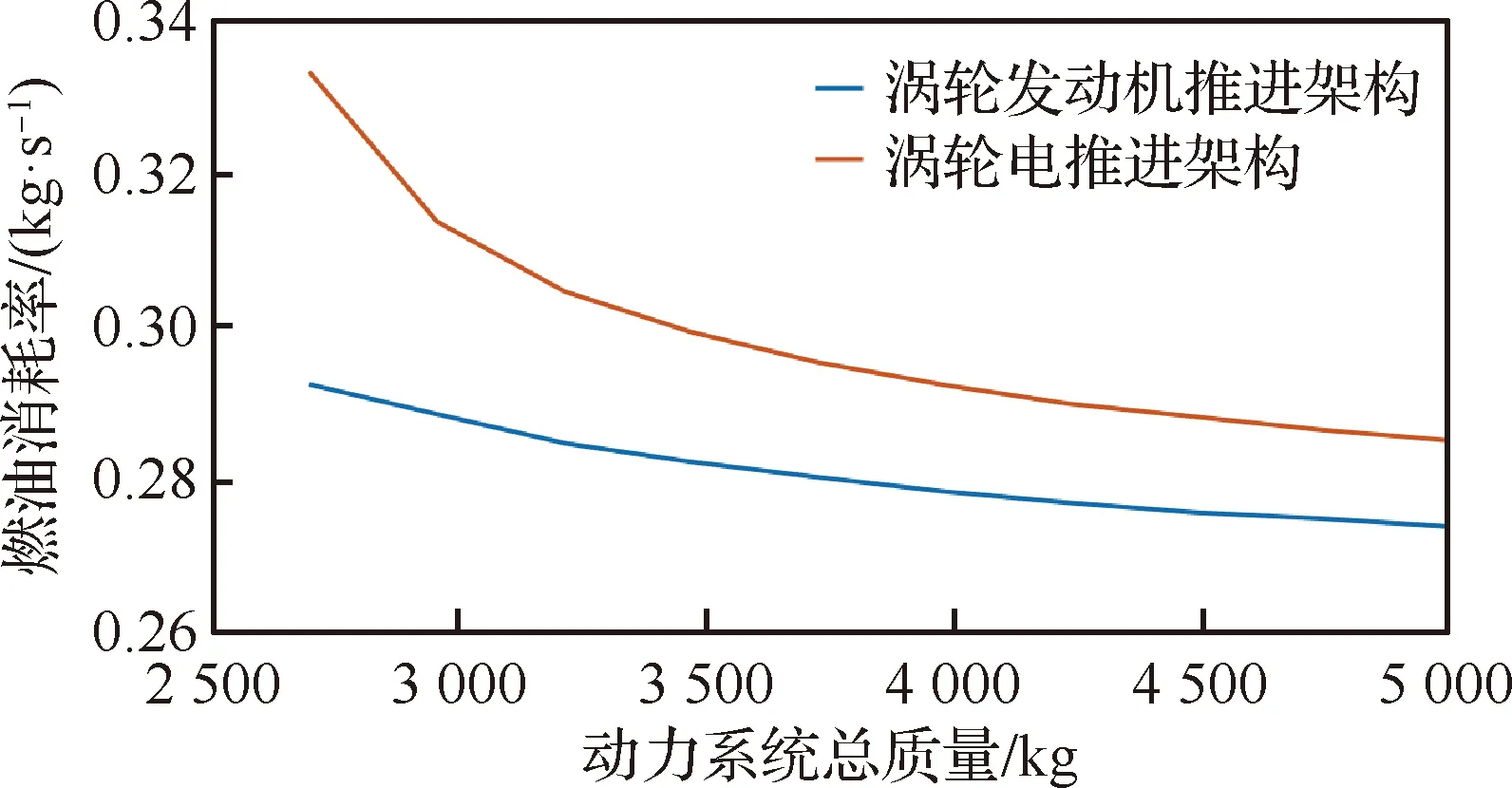
图27 两种架构质量与燃油消耗率的关系
为了进一步得到动力系统主要部件的效率随总质量的变化关系,针对涡轮电推进架构进行了分析,结果如图28所示。

图28 涡轮电推进架构主要部件效率与系统总质量关系
从图28可以看出,如前文所述,电机与涵道风扇的效率随系统总质量的增大而增加,发电机与电动机的效率的变化幅度很小,基本维持在98%左右;但是涵道风扇的效率变化很大,在质量最小点处,涵道风扇的推进效率仅有80%,在质量最大点处,效率增大到了92.8%。
4 结 论
电推进飞机作为当前研究的热点,存在许多技术问题亟待解决,本文选择电推进飞机混合动力系统作为研究对象,开展了分布式混合电推进飞机电力系统综合优化和评估研究,所做的主要工作和主要结论总结如下:
1) 以未来的电推进大型客机高压直流供电分布式布局电气系统架构作为研究对象,参考地面交流电网的潮流分析方法,对飞机电网在负载功率平衡与不平衡状态和断路故障状态下的变化情况进行了分析,同时研究了母线电压等级对电网的影响。
2) 介绍了推进系统功率计算与电气系统能量传输集成的耦合计算方法。在此基础上,在SIMULINK环境下分别搭建了涡轮-电推进与纯电推进动力系统架构的仿真模型,分析了两种架构中各动力源部件的功率分配情况,比较了两种架构的推进功率与效率,分析了航程随电池容量与载荷质量的变化关系。
3) 建立了输电线与电机的参数化模型,利用符号规划算法对两种模型分别进行了优化分析。对集成的涡轮直接推进与涡轮电推进架构进行分析,得到了其质量与效率的权衡优化结果。
未来的研究方向考虑在分布式多涵道风扇电推进飞机动力系统配置下,采用不同气动外形和动力配置的飞机构型进行动力系统综合分析,耦合如边界层吸入(BLI)等因素的影响来研究其与动力系统的相互作用,同时建立其能量优化耦合模型进行分析求解,在以上基础上考虑系统可靠性指标的综合多目标优化。
