多局部节点异步抗差航迹关联算法
2021-07-07衣晓杜金鹏张天舒
衣晓,杜金鹏,张天舒
海军航空大学,烟台 264001
在分布式多传感器信息融合系统[1]中,多局部节点情况下的航迹关联[2]问题一直是重要的研究内容。由于观测区域不完全重合,各局部节点获取的航迹数目不同,上报目标不完全一致的现象时常发生;且多局部节点航迹关联受航迹异步[3-4]与系统误差的影响更为明显。
针对航迹异步问题,文献[5]提出一种以最小二乘法为基础的变异蚁群算法;文献[6]利用顺序成对关联思想,将关联问题转化为广义似然比检验;文献[7]通过把局部航迹描述为集合,引入最优次模式分配(OSPA)距离进行关联。传统算法均是利用时域配准[8]解决异步航迹关联问题,但由于多局部节点数目较多,时域配准的处理方法会导致运算量迅速增加,且时间同步过程中的误差累积会大大降低关联效果。加之系统误差的存在使得航迹关联问题与误差配准[9-10]问题互为前提,上述算法的性能[11]将会大幅下降。
为克服系统误差的影响,文献[12]将航迹序列灰化,用灰色区域覆盖系统误差,利用区间数的相离度进行关联;文献[13]利用高斯随机矢量的统计特征,提出顺序成对关联思想的关联算法;文献[14]则利用真实状态对消得到等价量测方程,进行分级聚类。通过将系统误差转化为旋转量和平移量,文献[15-16]分别提出一种基于Fourier变换和Radon变换的航迹对准关联技术。考虑到系统误差主要影响目标的绝对位置而非相对位置,文献[17]利用目标拓扑结构的空间不变性,根据邻近目标间平均拓扑距离进行关联;文献[18]分析了虚警漏报导致的拓扑结构成员个数不一致的问题,并给出了初步的判别方法;文献[19]通过拓扑特征与最佳子模式分配度量距离相结合,进一步提高了算法性能;文献[20]则利用非刚性变换描述航迹间的结构差异,建立混合整数非线性规划模型进行航迹关联。
针对多局部节点航迹关联问题,文献[21]以灰关联度作为全局统计量构造多维灰色关联度矩阵,利用多维分配进行航迹关联。考虑到新目标增加的情况,文献[22]通过对测量集合和航迹集合合并,将多维分配的静态结果扩展为动态多维分配,提高了算法的稳定性。通过将模糊集理论[23]应用于数据关联,文献[24]提出了多传感器模糊数据融合模型和准则,利用数据关联的静态部分得出量测组合序列和多维分配最优解,利用动态部分估计目标实时状态,文献[25]则提出一种基于模糊遗传算法的多传感器数据关联方法。
传统算法对航迹异步、系统误差、多局部节点航迹关联等问题提出了不同解决方案,但各算法侧重点单一,且多局部节点观测区域不同导致的上报航迹集合不完全一致的问题未得到有效解决。
为解决航迹异步与系统误差并存且上报航迹不完全一致情况下的多局部节点航迹关联问题,本文提出一种基于区间离散度的多局部节点航迹关联算法。针对航迹异步问题,定义不依托时间变量的离散度指标,实现异步航迹的直接关联;针对系统误差的存在,提出区间化方法,通过概率密度函数的累次积分表征系统误差的不确定性;针对上报航迹不完全一致问题,设置零号航迹参与多维分配,实现全部航迹的有效关联。通过实验验证,算法可在航迹异步与系统误差并存的情况下实现多局部节点航迹的准确关联,有效解决上报航迹不完全一致的问题。且不同于传统算法性能受目标密集程度影响的特点,局部节点或目标数目的增加会提高本文算法的正确关联率。
1 航迹关联判别量的确立
1.1 航迹关联原理分析
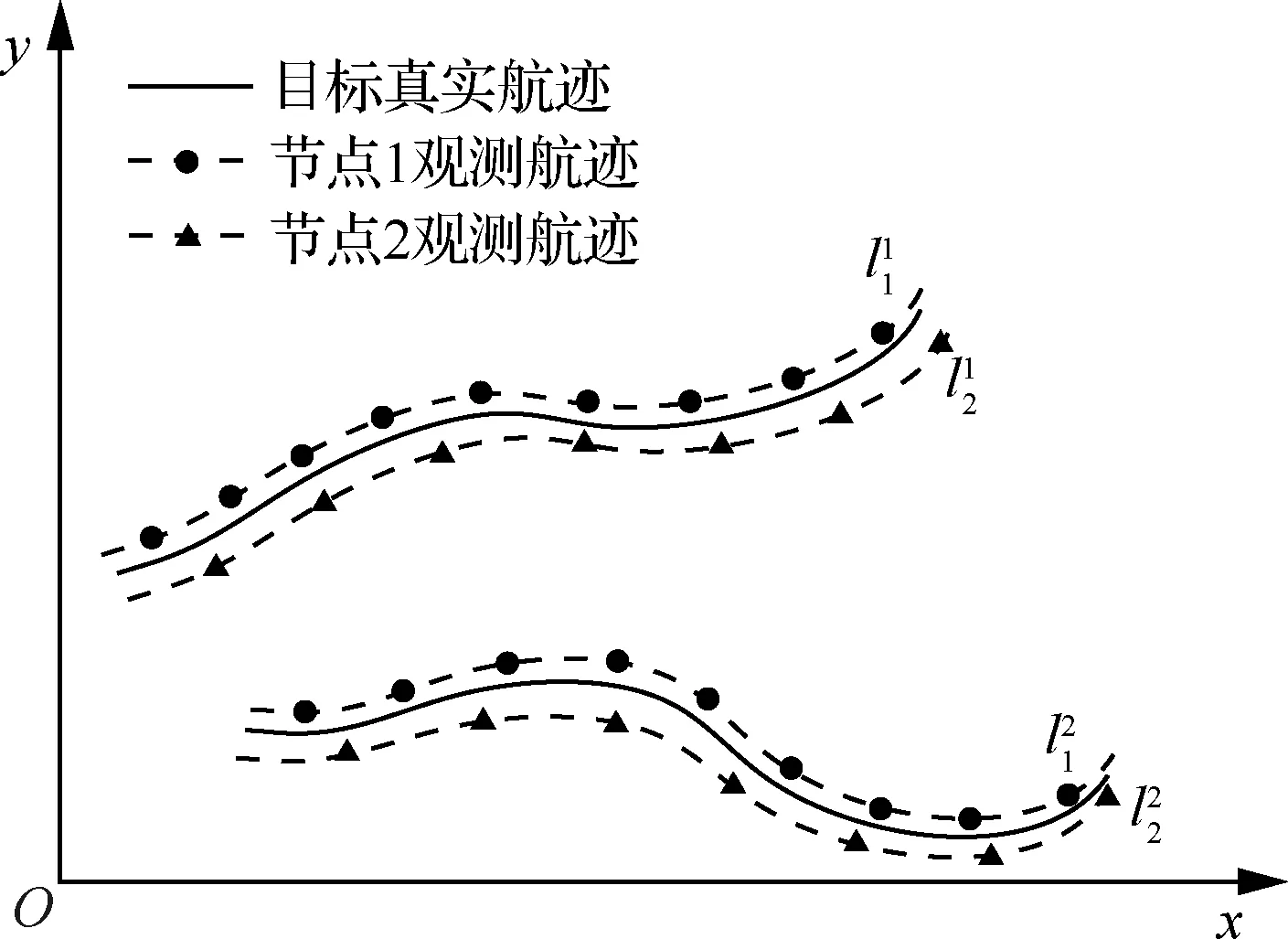
图1 航迹关联原理示意图
直观上看空间距离接近的航迹为同源航迹。对航迹间空间距离定义形式的不同导致关联算法多样,但均要求序列长度相等且各数据点观测时刻一致,因此传统算法对异步航迹关联必须进行时域配准处理。
1.2 空间位置与离散度
航迹序列反映到空间坐标系中的具体形式是坐标数值,同源航迹序列中的数据点是不同节点对同一目标观测而来,则从坐标数值角度而言,数据较为集中,离散度相对较小。
数学中离散随机变量的离散度定义[26]为:设变量ξ取值离散,其取值集合记为ξ={x1,x2,…,xn},则离散度为
(1)
从数学表达式中不难发现,离散度求解过程中的均值等价于“空间位置中心”,方差实为各离散点到“空间位置中心”距离的平方和,故离散度反应的离散点到位置中心总的偏离程度与距离受空间位置影响产生的变化具有一致性,空间距离越近,离散度越小。
以二维空间中连续变化的5组随机等长数列为例,如表1所示,其中,参考数列标号为1~4,比较数列标号为5,分别计算参考数列与比较数列的欧式距离di5与离散度Vi5,结果见表2。
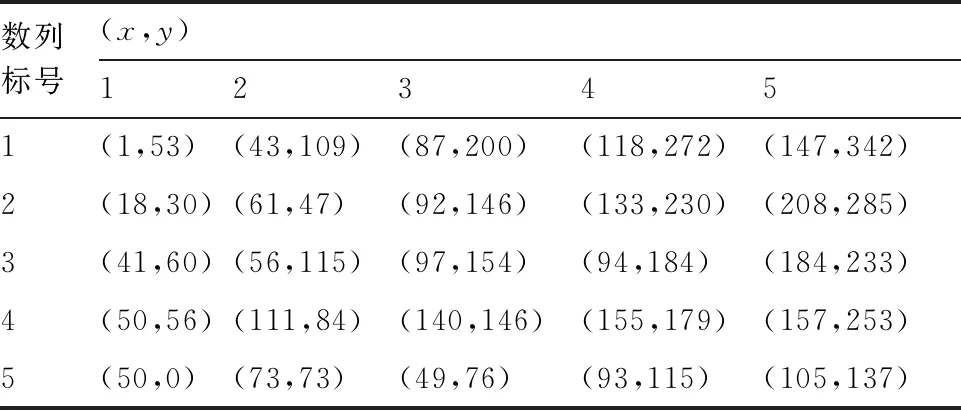
表1 随机数列数据

表2 数列距离与离散度
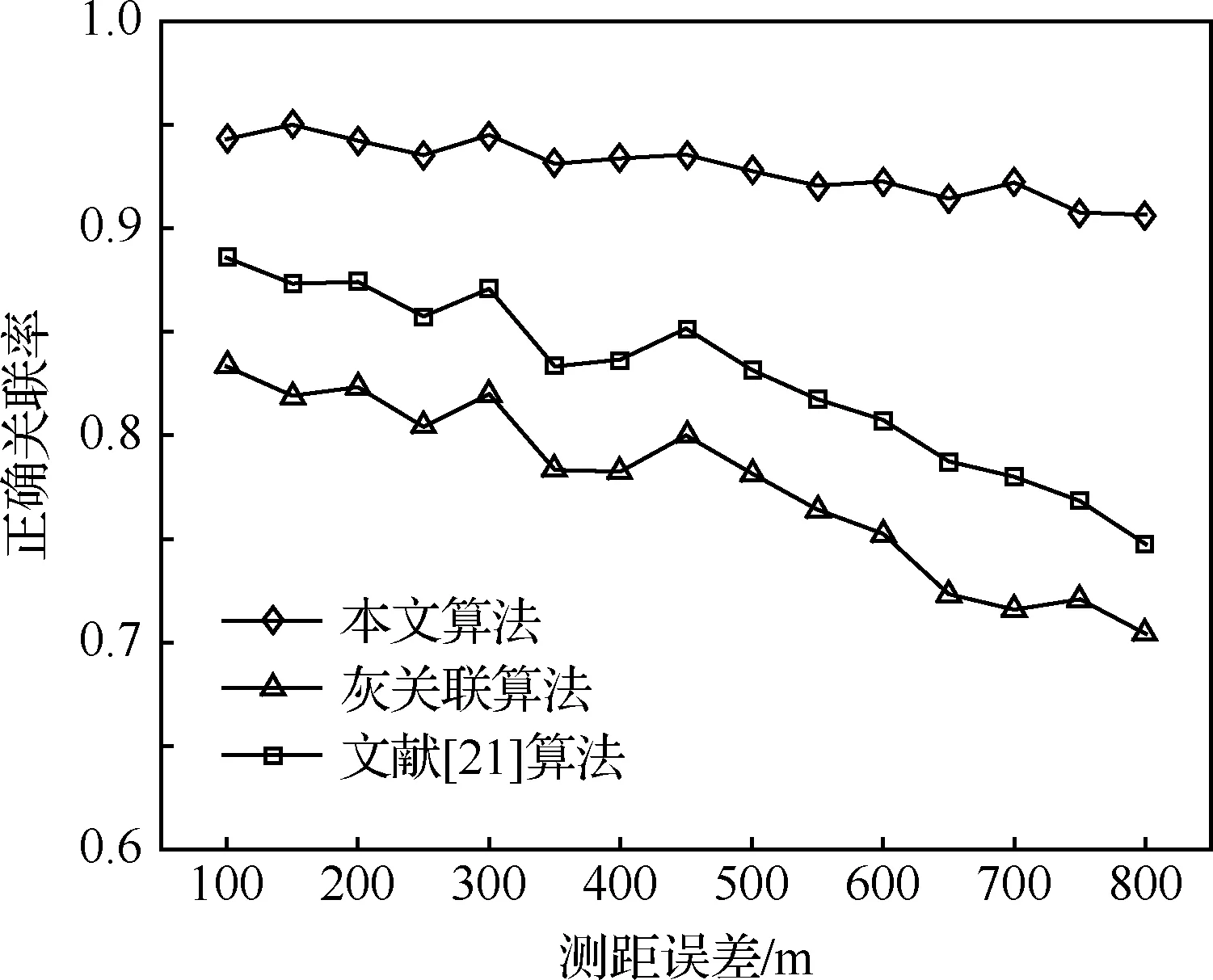
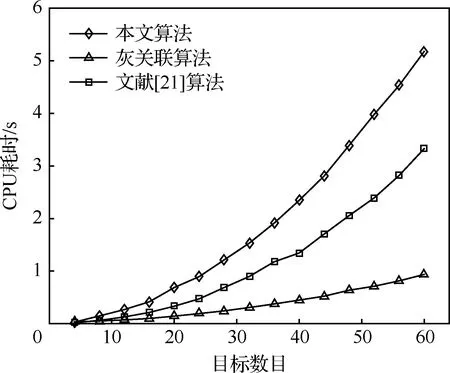
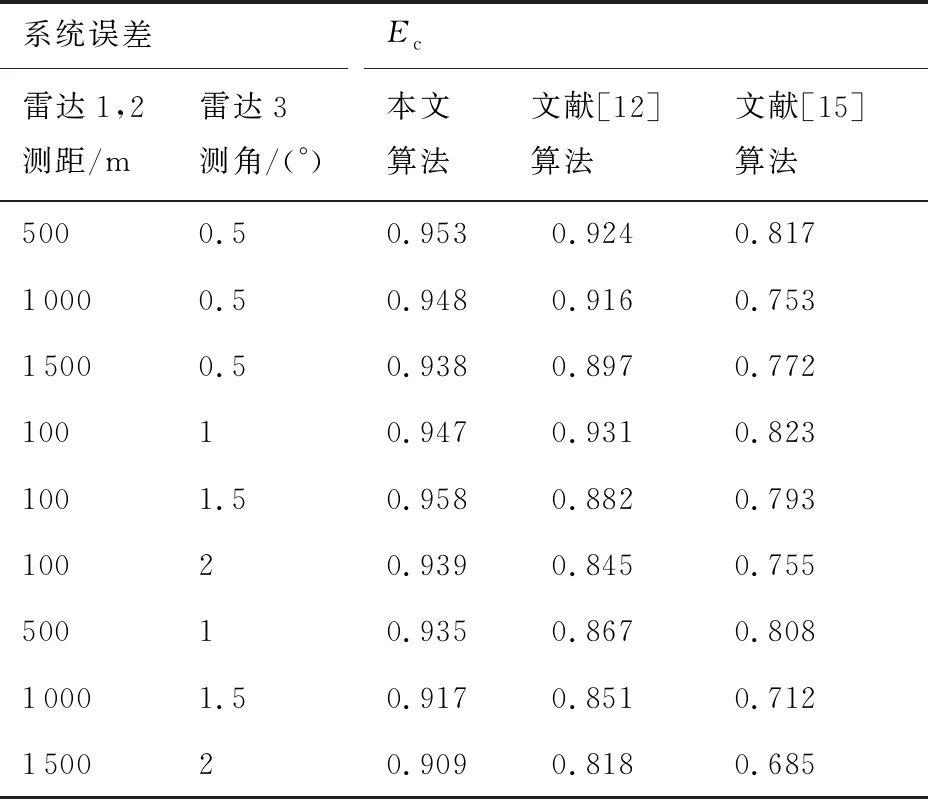
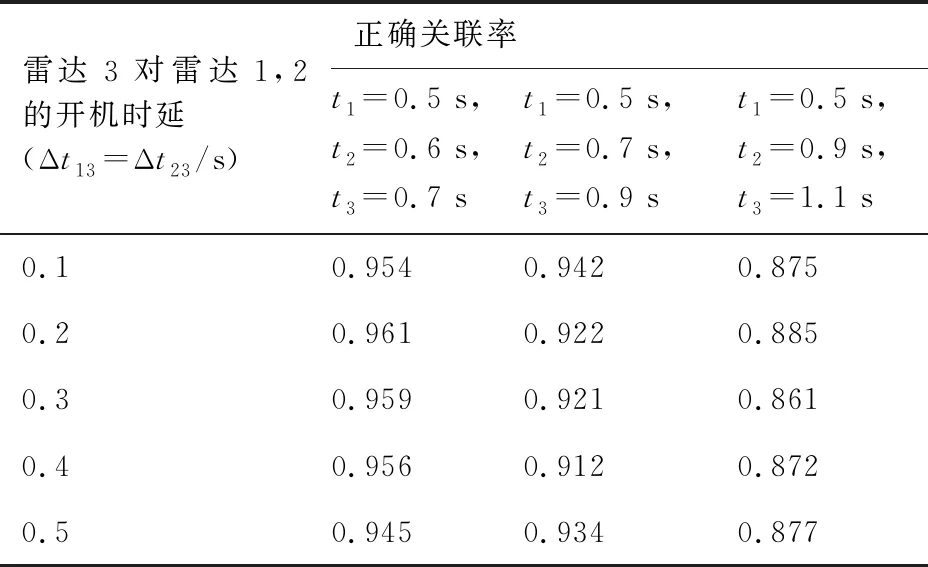
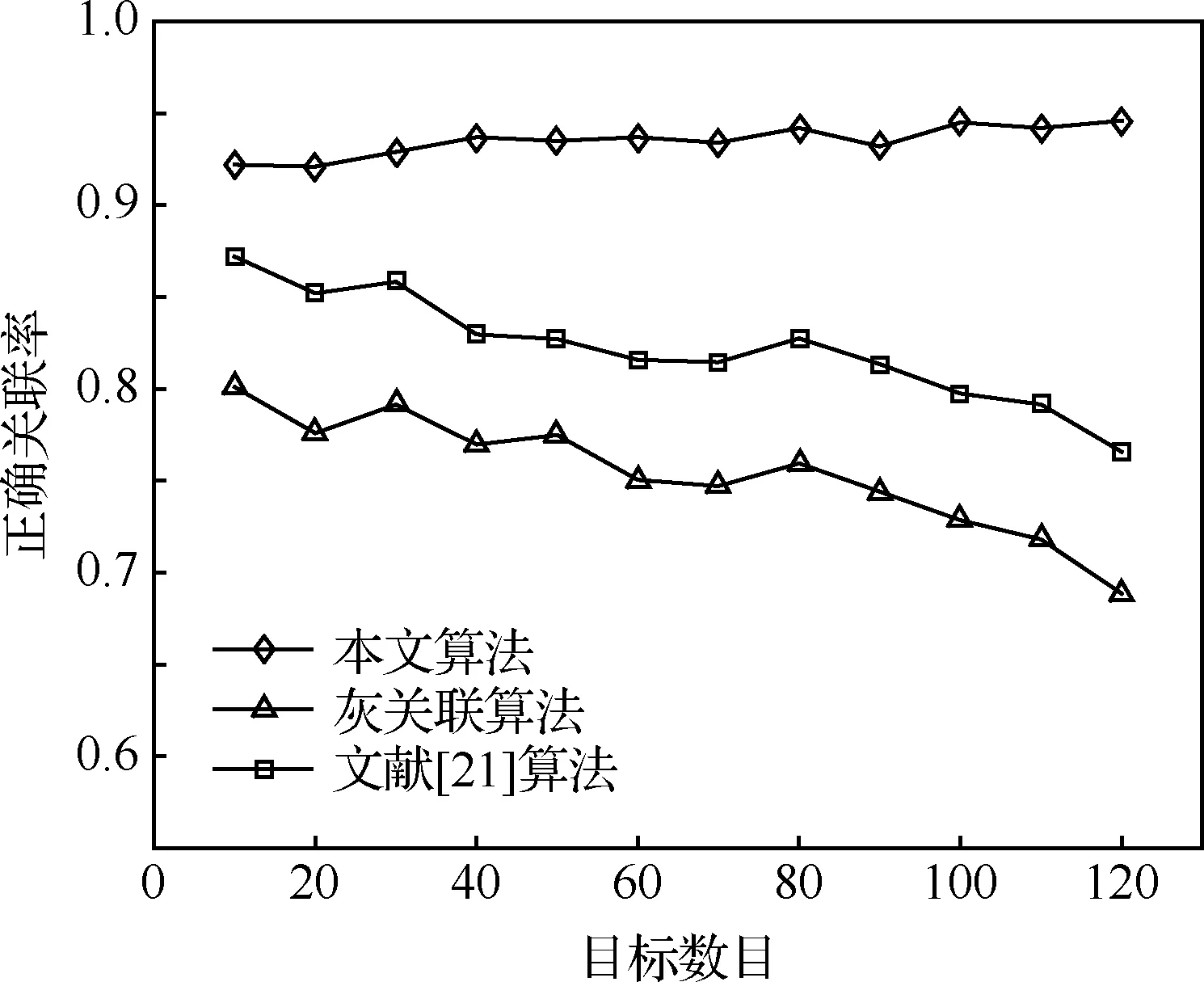
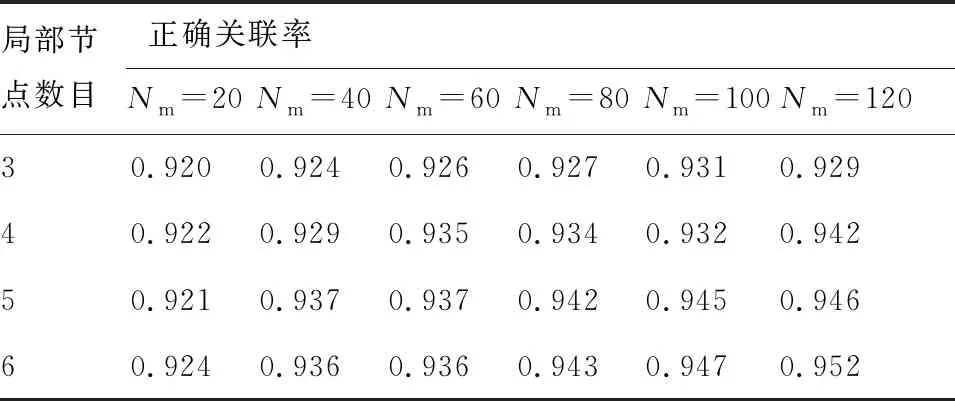
根据表2计算结果,有:d35 对含有未知系统误差的航迹做区间化处理,处理后的航迹序列各元素为取值连续的区间数,对集合元素离散、各元素为取值连续的区间数的数据集定义区间离散度如下。 (2) 区间方差为 (3) 区间离散度为 (4) 式中: 假设由M(M≥3)个局部节点对多个目标进行跟踪,所有局部节点不仅存在公共观测区域,也可能存在独立观测区域。图2表示了M=3情况下的观测区域示意图。 图2 观测区域示意图 图中Ⅰ、Ⅱ、Ⅲ区为两个局部节点的公共观测区域,Ⅳ区为3个局部节点的公共观测区域,空白区为各局部节点的独立观测区域。 在进行多局部节点航迹关联时,采用传统多维分配法构造的全局统计量只对Ⅳ区航迹进行关联,对Ⅰ、Ⅱ、Ⅲ区航迹未处理,出现“航迹遗漏”现象。 而传统的两两关联算法利用等价关系的可传递性依次进行两两关联检测。以局部节点1、2的航迹先进行关联,局部节点2、3的航迹再进行关联为例,关联结束后,Ⅰ、Ⅲ、Ⅳ区的航迹被成功关联,但Ⅱ区的航迹未被关联,出现“航迹遗漏”现象。 上述“航迹遗漏”现象实际是由各局部节点观测区域不同,上报航迹集合不完全一致导致的;且此现象会随局部节点数目的增加而加重。故多局部节点上报航迹不一致情况下的航迹关联问题需作单独处理。 假设M个异地配置的局部节点位于公共笛卡尔坐标系中,坐标记为(xs,ys),s=1,2,…,M,各局部节点所得航迹标号集合为 U1={1,2,…,n1},…,UM={1,2,…,nM} (5) 所得航迹序列包含距离估计和方位角估计。根据系统误差对距离和方位角估计进行区间化处理,对所得混合区间型数据集计算区间离散度,记为λi1i2…iM。 由于离散度[27]表征数据的离散程度,λi1i2…iM越小说明航迹i1,i2,…,iM为同源航迹的可能性越大,故利用多维分配法构建目标函数,即可求解航迹关联最优解。 在二维平面坐标下某目标的真实距离和方位角分别为ρ、θ,考虑到局部节点受到缓慢变化的系统偏差的影响,根据局部节点可能的系统误差最大值,在给定系统误差偏差范围内研究航迹真值分布的特点。假设局部节点的系统误差大于0,记测距和测角系统误差最大值为Δρm、Δθm,则在k时刻的量测值为 (6) 式中:Δρ、Δθ、υρ、υθ为局部节点在距离和方位角上的系统误差和随机量测误差。 不考虑随机量测误差的影响,则目标真值为 (7) 图3 系统误差示意图 考虑到单次量测的随机性,目标落于区域G内各点处的概率不同,设目标距离随机变量和方位角随机变量服从高斯分布,根据3σ原则,可得目标二维极坐标服从的分布函数为 (8) 根据系统误差对航迹序列区间化得到区间序列 距离和方位角量测值在各区间服从的概率密度函数记为 (9) 由于极坐标与直角坐标存在如下关系 (10) 以x分量为例,根据区间离散度定义可知直角坐标系下区间离散度为累次积分形式,得区间均值为 (11) 区间方差为 (12) 由于距离和方位角测量相互独立,式(11)和式(12)中fk(ρ,θ)为联合概率密度函数,有 fk(ρ,θ)=fk(ρ)·fk(θ)= (13) 当局部节点可获取三维信息(距离、方位角、俯仰角)时,根据三维坐标转换公式和量测独立性,其区间均值、区间方差、联合概率密度函数的计算方式类似。 以二维情况为例,设T为融合中心的处理周期,在第k个处理周期[(k-1)T,kT]内,从M个局部节点中各取一条待关联航迹序列 (14) 式中: 零号航迹设置规则: 1)M个局部节点均设置一条零号航迹,标号为0。 3) 包含零号航迹的航迹组合的区间离散度取值单独定义。 (15) 式中:δ为任意取值的极小量。 其余包含k(k=1,2,…,M-1)条零号航迹的航迹组合的区间离散度取值与式(15)类似。 定义二进制变量 (16) 于是,多局部节点航迹关联问题转化为全体航迹的多维分配问题,即 (17) 其约束条件为 (18) 对第s个局部节点中任意取定的航迹is而言,航迹组合多样,但式(18)约束各种组合对应的二进制变量求和为1,根据式(16)定义可知仅同源航迹组合二进制变量取值为1,故约束条件可有效保证同源航迹组合判定结果的唯一性。 此类多维分配问题的求解,可用松弛算法等经典解决方法,此处不再赘述。 算法的流程如图4所示。 图4 算法流程图 设在T=0 s时随机产生60个目标,目标初始位置在区域[0,100] km×[0,100] km中均匀分布,目标运动模型采用二维平面匀速直线运动模型,且目标初始航向在0~2π rad内随机分布,目标初始速度在300~500 m/s内随机分布,目标持续运动时间为40 s。 为体现多局部节点观测区域不完全重合的特点,设雷达无法观测全部目标航迹,只能随机观测部分目标航迹,且雷达1、2、3观测航迹数目分别占目标航迹总数的90%、80%、70%。 采用3种关联率对航迹关联结果进行评价,记正确关联概率为Ec,错误关联概率为Ee,漏关联概率为Es。 仿真过程中,对于不支持多局部节点直接关联的算法,采用两局部节点的顺序两两关联检验;且将2.1节中描述的“遗漏航迹”视为漏关联,相应“遗漏关联概率”计入Es。 同时改变3部雷达测距的量测误差标准差,研究3种算法正确关联率的变化。 从图5中可以看出,随着测距随机误差的增大,3种算法的正确关联率均下降,其中使用多维分配的本文算法和文献[21]算法的正确关联率高于顺序两两关联算法。这是由于多维分配寻求全局最优解,更适合多局部节点下的航迹关联。由于文献[21]利用灰关联度构建多维矩阵,其算法变化趋势与灰关联算法相似。 图5 关联结果随测距误差的变化 改变3部雷达测角的量测误差标准差,研究3种算法关联率的变化,如表3所示。 表3 不同测角误差下的关联率 从表3中可以看出,本文算法的正确关联率最高,且本文算法的漏关联率明显低于文献[21]算法和灰关联算法。对于多局部节点航迹关联,由于上报航迹集合不完全一致,文献[21]算法和灰关联算法中均存在大量“遗漏航迹”未参与关联。从表3结果来看,本文设置零号航迹参与多维分配的方法可有效抑制“航迹遗漏”现象,解决多局部节点上报航迹不一致的问题。 图6给出了算法耗时的比较结果。以本文3个局部节点为例,传统的顺序两两关联算法利用等价关系的传递性,只需顺序进行两轮航迹关联,故耗时较低。而本文算法和文献[21]算法使用多维分配方法,其求解复杂度随着问题规模的增大呈指数增长,算法耗时普遍较高。由于本文算法计算过程涉及大量积分计算,且零号航迹的设置进一步增大了运算规模,故比一般的多维分配算法耗时更多。 图6 算法耗时对比 改变仿真环境中雷达1、2的测距系统误差和雷达3的测角系统误差,比较算法的抗差性能。 表4中3种算法均无需事先校正雷达探测系统误差,避免了传统航迹关联与误差配准相矛盾的问题。从表4中可以看出,本文算法抗差性能最佳,文献[15]算法受系统误差的影响较大。 表4 不同系统误差下的关联率 算法[15]利用傅里叶变换估计补偿航迹因系统误差带来的旋转量和平移量,由于较大的系统误差会在一定程度上导致航迹的略微变形,此时对旋转平移量的估计误差较大,故关联性能有所下降。 图7给出了3部雷达不同采样率之比对算法的影响。可以看出,随着采样率之比的增加,3种算法的正确关联率均下降,且文献[5]和文献[8]中算法下降趋势较快。 文献[5]和文献[8]中算法是典型的通过时域配准对异步航迹进行关联的算法。当采样率之比逐渐增大时,时间同步过程中需要滤波插值的航迹点数目增加,使得滤波误差迅速累积,影响算法关联效果。 为研究本文算法对系统误差下异步航迹直接关联的有效性,在存在系统误差的前提下,改变仿真环境中3部雷达的采样周期与时延进行仿真验证,如表5所示。 表5 不同采样周期和开机时延的正确关联率 从表5中可以看出,在存在系统误差的前提下,雷达开机时延并未产生明显影响。这是由于本文算法所用指标离散度不依托时间变量,一定范围内的开机时延只造成数据点在时间上的错位,并不影响数据分布的离散度,其中,t1、t1、t3为雷达1、2、3采样周期。 由于离散度属于统计学度量,其度量精度与数据点数目有关,采样周期越长,数据量越少,对离散度的刻画越不准确,故随着采样周期增大,算法正确关联率有所下降。 改变仿真环境中目标航迹总数,研究目标密集程度对算法性能的影响。 从图8中可以看出,在目标数目增多时,传统灰关联算法和文献[21]算法的正确关联率有所下降,而本文算法的正确关联率反而上升。 图8 不同目标数目的正确关联率对比 表6给出了不同局部节点和目标数目Nm下本文算法的正确关联率。 表6 不同局部节点和目标数目下的正确关联率 从表6中可以看出,本文算法在局部节点和目标数目增加时,正确关联率有所提高。从数理统计原理来看,利用离散度表征集合中数据的分散程度时,一定程度上航迹数目的增加会增大混合区间数据集的样本量,进而提高离散度对同源航迹数据集合中非同源航迹数据的分辨精度,有利于算法性能的提升。 1) 提出一种基于区间序列离散度的多局部节点异步抗差航迹关联算法,定义区间型数据集离散度的具体度量指标和航迹序列区间化的方法,并通过概率密度函数累次积分量化系统误差的影响。 2) 算法无需时域配准,可对多局部节点下存在系统误差的异步航迹直接进行准确关联,且零号航迹的设置可有效解决多局部节点上报目标航迹不一致的问题。 3) 与传统算法不同,本文算法的正确关联率随局部节点数目或目标数目的增加而提高。1.3 区间型数据集的离散度度量
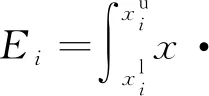
2 基于区间离散度的航迹关联算法
2.1 问题描述
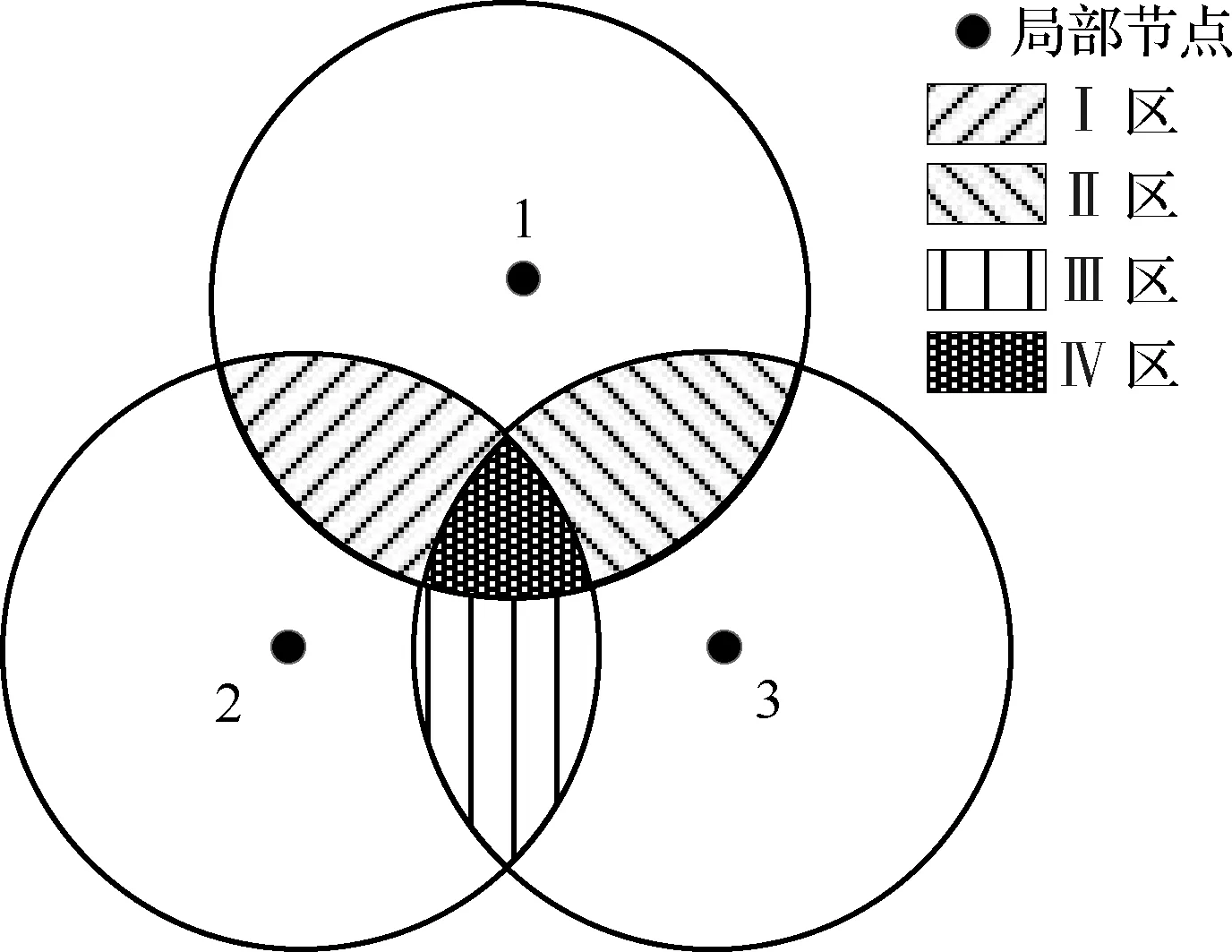
2.2 系统误差的区间化与累次积分
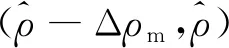
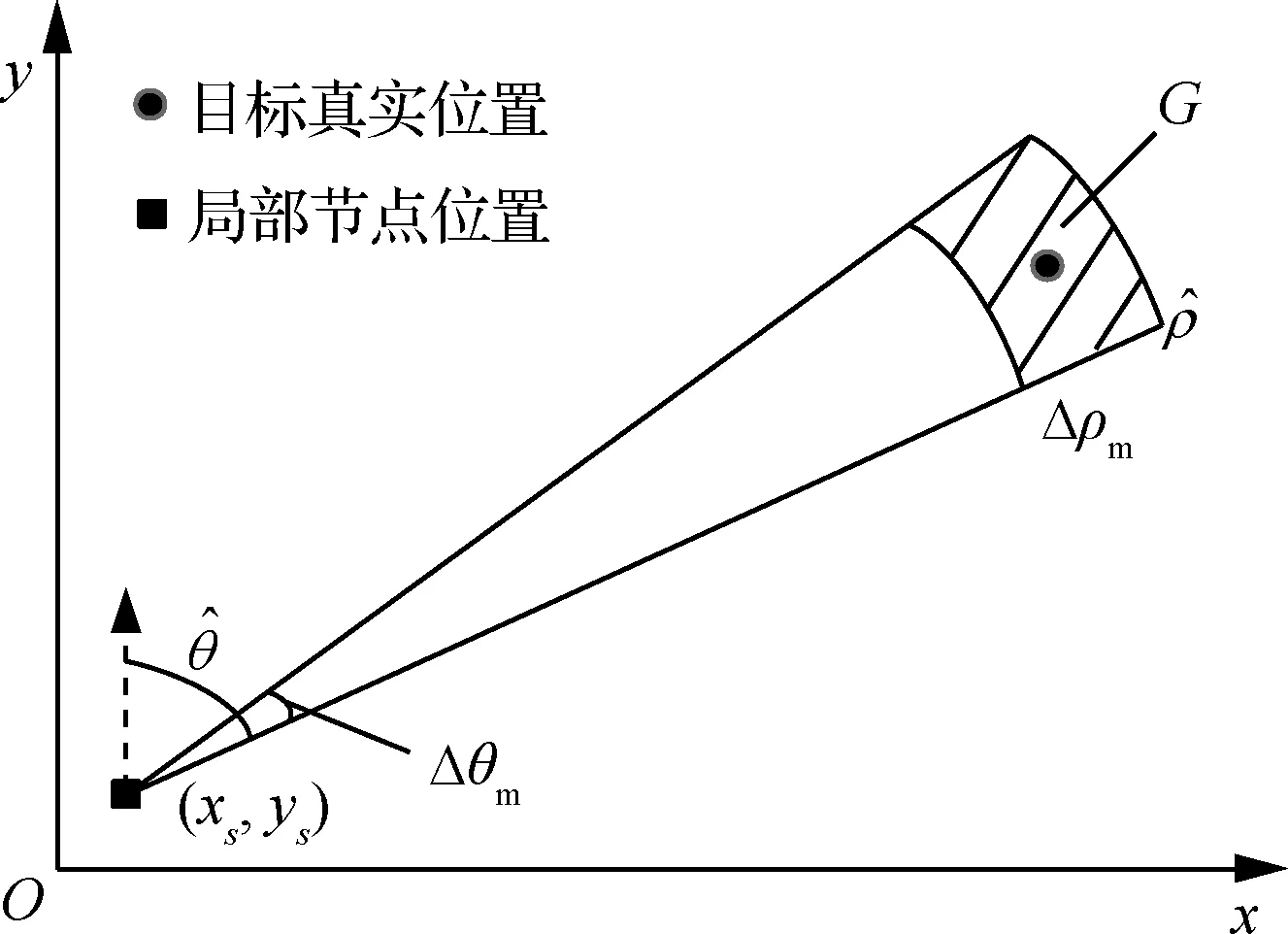
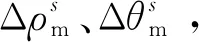
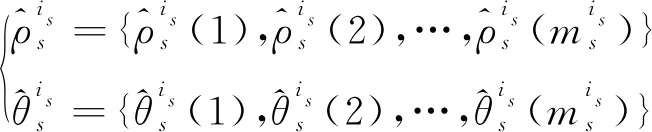
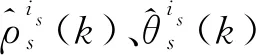
2.3 航迹关联判定
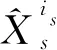
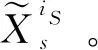
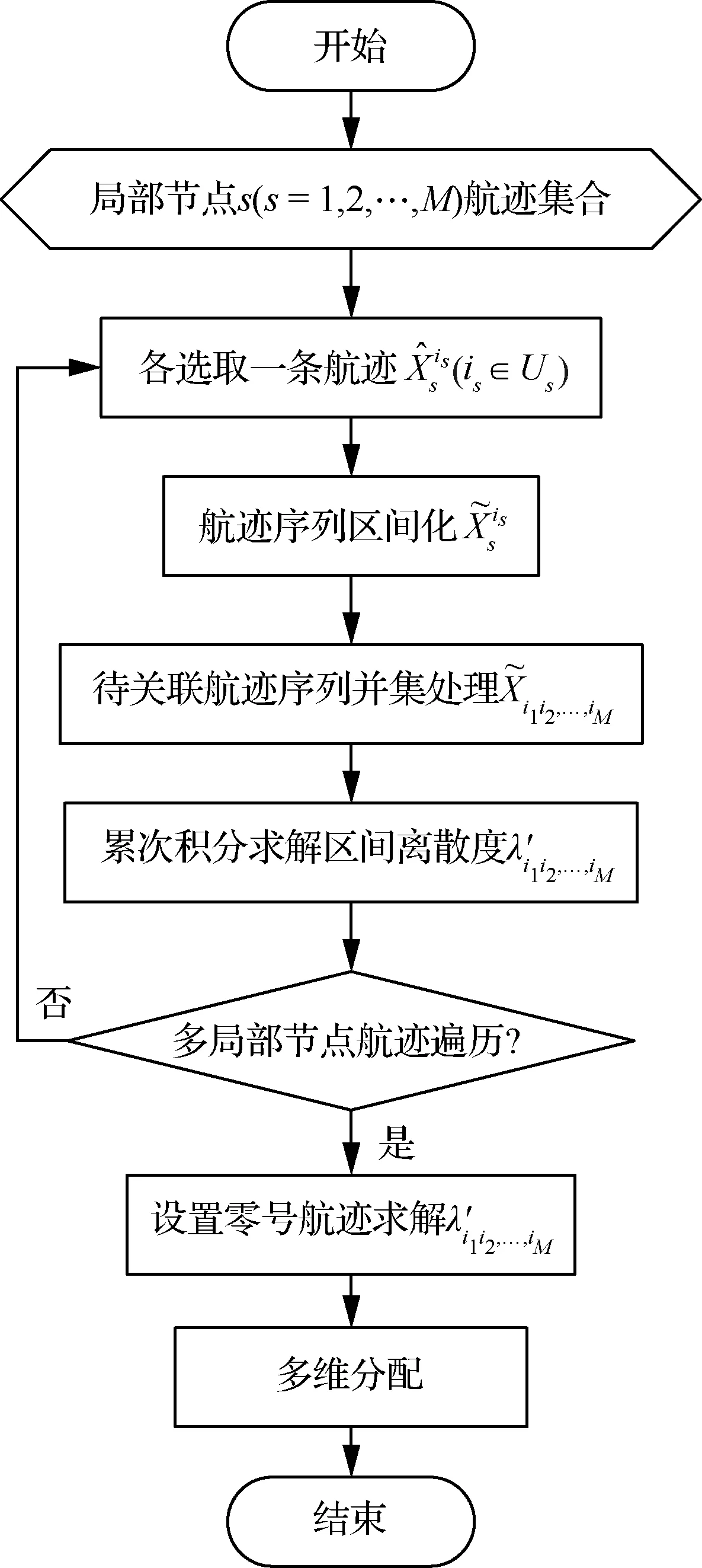
3 仿真验证与分析
3.1 仿真环境
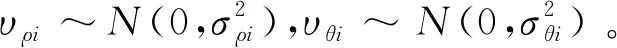
3.2 算法性能比较与分析
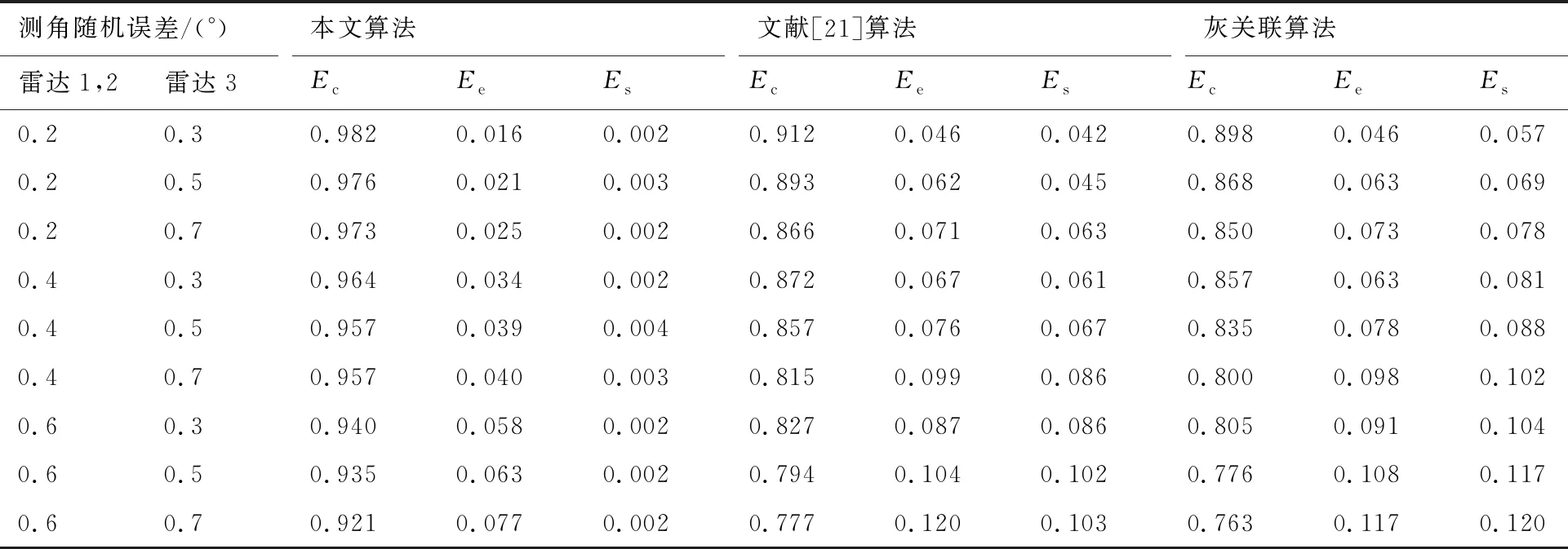
3.3 系统误差与航迹异步关联有效性分析
3.4 局部节点数目与目标密集程度的影响
4 结 论
