基于稀疏贝叶斯学习的字典失配杂波空时谱估计方法
2021-07-07章涛钟伦珑来燃郭骏骋
章涛,钟伦珑,来燃,郭骏骋
中国民航大学 天津市智能信号与图像处理重点实验室,天津 300300
空时自适应处理(Space-Time Adaptive Processing, STAP)是机载阵列雷达抑制杂波的一种有效方法[1-2]。STAP的杂波抑制性能主要取决于杂波协方差矩阵(Clutter-plus-noise Covariance Matrix, CCM)的估计精度。传统STAP方法采用统计估计的方法获得CCM估计值,若需保证输出信杂比相较最优值下降不超过3 dB,则至少需要系统自由度2倍数量的独立同分布(Independent Identically Distributed, IID)杂波样本[3]。然而在实际系统中,当杂波呈现非平稳或非均匀特性时,很难获得足够的IID样本,进而使得STAP杂波抑制性能严重损失[4]。
为了减少STAP所需杂波样本数量,研究人员提出了多种方法,主要包括降维STAP方法和降秩STAP方法。降维STAP方法利用与数据无关的变换降低接收数据维数,使得所需杂波样本数量为降维后数据维数的2倍,主要方法包括:辅助通道处理(Auxiliary Channel Processing, ACP)方法[5]、扩展因子化(Extended Factored Approach, EFA)方法[6]、广义多波束(Generalized Multiple Beams, GMB)方法[7]等,但这类方法不可避免地存在系统自由度损失。降秩STAP方法则利用与数据有关的变换对接收数据进行处理,使得所需杂波样本数降低为杂波秩的2倍,主要方法包括:正交投影处理(Orthogonal Projection Processor, OPP)方法[3]、最小功率特征对消(Minimum Power Eigen canceller, MPE)方法[8]、多级维纳滤波(Multistage Winer Filter, MWF)方法[9]等,但是这类方法的性能依赖于杂波秩,在实际杂波环境中很难准确估计杂波秩。
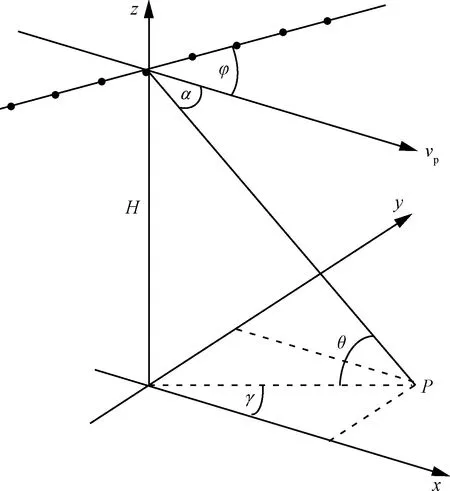
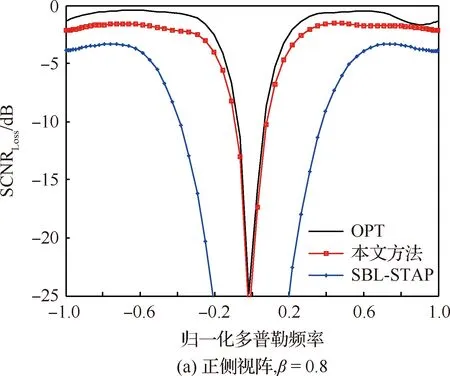
近年来,稀疏恢复方法在信号处理领域快速发展[10-11]。由于稀疏恢复方法可以使用很少样本精确地恢复未知稀疏信号,已成为机载雷达杂波抑制的研究热点[12-13]。目前比较有代表性的杂波空时谱稀疏恢复方法包括:文献[14]提出了利用1范数最小化实现空时谱稀疏恢复的凸优化方法。文献[15-17]提出了基于p范数(0 稀疏恢复STAP方法将杂波信号看作在某些已知基向量下是稀疏的,这些基向量被称为稀疏恢复字典。由于空时平面被离散地划分为若干个网格点来构建空时导向矢量字典,离散化的字典与连续的杂波谱参数间的误差问题被称作字典失配问题,严重影响稀疏恢复效果。在正侧视阵情况下,若稀疏恢复空时平面网格划分与杂波脊斜率不匹配;或是当阵列为非正侧视架设,杂波脊呈曲线形式时,则杂波大多不会位于预先离散化的空时平面网格点上,字典失配将严重影响稀疏恢复STAP的杂波抑制性能。虽然增加空时导向矢量划分密度可以减少字典失配的影响[19],但字典网格间隔越小,空时导向矢量的相关性越强,会导致稀疏恢复性能下降,而且计算量也将大幅增加[10]。 目前,针对稀疏恢复中字典失配问题的研究主要集中在一维离散参数字典的补偿方面,如:文献[20]提出了一种稀疏总体最小二乘(Sparse Total Least-Squares, STLS)方法,结合动态字典模型解决一维波达方向(Direction of Arrival, DOA)估计中的字典失配问题。文献[21]提出利用基追踪方法解决DOA估计中的字典失配问题。为了避免正则化参数难以确定的问题,文献[22] 提出了一种利用动态字典解决字典失配问题的稀疏贝叶斯学习(Off-Gird Sparse Bayesian Inference, OGSBI)方法,但该方法仅能处理一维离散参数字典失配问题,不能直接用于存在二维字典失配的杂波空时谱稀疏恢复。目前针对杂波空时谱稀疏恢复中二维离散参数字典失配问题的研究还比较少,且有一定的适用局限性。例如,文献[23]在2013年首次提出了杂波空时谱估计中存在字典失配问题,并给出了一种利用字典学习的失配补偿方法,但该方法仅适用于正侧视阵情况。文献[24]提出了利用载机平台运动参数获得杂波脊先验信息后细化字典间隔来解决字典失配问题的方法,但这种方法依赖载机平台传感器,有些情况并不适用。文献[25]提出了基于正交匹配追踪(Orthogonal Matching Pursuit, OMP)的方法,通过梯度下降方法寻找与真实模型匹配的字典向量来解决字典失配问题,但OMP方法的性能对参数选择依赖性较高。 针对目前已有的字典失配情况下稀疏恢复STAP算法存在仅适用于正侧视阵、依赖机载平台其他传感器、算法性能对参数选择敏感等问题,本文将OGSBI方法扩展到二维字典失配的情况,提出了一种解决空时二维字典失配的稀疏贝叶斯学习STAP方法。本方法的主要创新性包括:① 针 对空时二维参数字典失配,建立了一种利用二维泰勒级数的空时二维字典失配误差动态模型;② 将空时二维字典失配误差作为超参数,给出了期望最大化(Expectation-Maximization, EM)方法迭代估计公式,进而修正空时二维参数字典失配误差, 最后利用修正后的空时导向矢量字典估计杂波协方差矩阵及杂波空时谱。实验表明,本文方法能够有效提高杂波谱稀疏恢复精度,STAP处理性能优于已有字典预先离散化处理的稀疏贝叶斯学习STAP算法。 考虑采用均匀线阵的机载阵列雷达,如图1所示,阵列天线由M个阵元组成,阵元间距d=λ/2,λ为雷达工作波长;H为载机平台高度;vp为速度,且沿x轴运动;α为杂波散射点P与飞行方向间的夹角;θ和γ分别为俯仰角和方位角;φ为阵列轴线与飞行方向间的夹角,即当φ=0°时为正侧视阵模式,φ=90°为正前视阵模式。 图1 机载雷达阵列几何结构 雷达在每个相干处理周期内发射N个脉冲,脉冲重复频率为fr。当不存在距离模糊时,对于不存在目标的距离单元的回波进行采样可以获得一个杂波观测矢量数据(通常称为一个空时快拍数据)x∈CNM×1 x=xc+n (1) 式中:xc为杂波分量;n为噪声分量。每个距离单元的杂波可以看成是多个杂波散射体空时响应的叠加,即 (2) 式中:Nc表示杂波散射体数量;ai、fd,i和fs,i分别表示复幅度、多普勒频率和空间频率。s(fd,i,fs,i)∈CNM×1称为空时导向矢量,即s(fd,i,fs,i)=sd,i(fd,i)⊗ss,i(fs,i),⊗表示Kronecker积运算。其中: 空间导向矢量ss,i(fs,i)定义为 ss,i(fs,i)=[1,exp(j2πfs,i),…, exp(j2π(M-1)fs,i)]T (3) 时间导向矢量sd,i(fd,i)定义为 sd,i(fd,i)=[1,exp(j2πfd,i),…, exp(j2π(N-1)fd,i)]T (4) 空间频率fs,i满足 fs,i=cos(γi-φ) (5) 多普勒频率fd,i满足 (6) 在归一化空间频率和多普勒频率构成的空时平面上,杂波脊的斜率(折叠系数)为 (7) CCM定义为 R=E(xxH) (8) 在噪声向量n假设为零均值高斯分布的情况下,基于最大信杂噪比(Signal-to-Clutter-plus-Noise Ratio, SCNR)准则,可以得到自适应权矢量的STAP输出为 y=wHx (9) 式中:自适应权矢量w可以通过CCM计算获得,即 (10) 其中:st(fd,fs)为待检测单元的空时导向矢量。由于CCM未知,实际系统中可以通过与目标检测单元杂波分布相同的杂波样本计算CCM的估计值,如 (11) 其中:训练样本数L需大于系统自由度的2倍,这种方法称作采样矩阵求逆(Sample Matrix Inversion, SMI) STAP方法[1]。但对于非均匀、非平稳的杂波环境不同距离单元杂波数据难以构成足够的IID样本,因此这种方法在有些情况下并不适用[12-13]。 基于杂波谱稀疏恢复的STAP方法将上述方法中的CCM估计通过稀疏恢复的方法实现,可有效减少所需IID杂波训练样本数[12-13]。这类方法首先将杂波谱空时平面划分为Ns×Nd的网格。其中,Ns=ρsM,Nd=ρdN,ρs和ρd为网格划分系数,且ρs>1,ρd>1。网格点所对应的空时导向矢量集合可以表示为 Ψ=[ψ1,ψ2,…,ψNs×Nd]=Sd⊗Ss (12) 式(12)在稀疏恢复STAP中被称为空时导向矢量字典,其中 Ss=[ss,1,ss,2,…,ss,Ns]∈CM×Ns (13) Sd=[sd,1,sd,2,…,sd,Nd]∈CN×Nd (14) 单快拍(Single Measurement Vector, SMV)杂波样本数据x的稀疏恢复模型可以表示为 x=Ψa+n (15) 式中:a=[a1,a2,…,aNsNd]T为稀疏恢复支撑集向量,其每一个非零元素表示一个对应的杂波单元。通过稀疏恢复理论,支撑集向量a可以通过下面最优化方法获得 (16) 通过稀疏恢复方法获得支撑集向量a后,CCM矩阵可通过式(17)重构获得 (17) 为了提高稀疏恢复性能,可以利用多快拍(Multiple Measurement Vector, MMV)杂波样本数据进行联合稀疏恢复。K个杂波样本数据X=[x1,x2,…,xK]∈CNM×K可以表示为 X=ΨA+N (18) 式中:A=[a1,a2,…,aK]为稀疏恢复的支撑集矩阵,其每个非零行表示一个对应的杂波单元;N=[n1,n2,…,nK]为噪声矩阵。通过联合稀疏恢复理论,支撑集矩阵A可以通过式(19)最优化方法获得 (19) 稀疏恢复STAP方法使用的空时导向矢量字典中空间频率和多普勒频率等间隔离散地分布在空时平面上。对于正侧视阵,且折叠系数β=1时,杂波脊位于空时平面对角线位置,正好位于空时平面网格点上,如图2(a)所示,字典中空时导向矢量可以准确地与杂波单元对应,此时不存在字典失配问题,STAP处理性能较好。当折叠系数β≠1即杂波脊不在空时平面对角线上,如图2(b)所示,或工作在非正侧视阵情况,杂波脊在空时平面上呈现曲线形式时,如图2(c)所示,可以看出杂波单元通常不能与空时导向矢量对应,字典失配将严重影响杂波谱稀疏恢复性能。 图2 杂波脊在空时平面上的分布示意图 (20) 利用空时二维动态字典估计字典失配误差Δfd和Δfs后,可得到失配补偿后的字典Φ=[Φ1,Φ2,…,ΦNsNd],即 Φ(Δfd,Δfs)=Ψ+Fdiag(Δfd)+Gdiag(Δfs) (21) 式中:Ψ为式(12)定义的失配字典。 (22) (23) (24) (25) 估计字典失配误差进行补偿后,式(15)改写为 x=Φ(Δfd,Δfs)a+n (26) 式(18)可以改写为 X=Φ(Δfd,Δfs)A+N (27) 本节以式(27)表示的MMV模型,给出字典失配误差估计及空时谱估计的稀疏贝叶斯学习算法,式(26)表示的SMV模型可由MMV模型方法中快拍数设置K=1得到。 噪声向量N假设为零均值复高斯白噪声,则 (28) p(X|A,Δfd,Δfs,λ0)= (29) 式中:λ0未知,假设服从伽马先验分布,即 p(λ0|c0,d0)=Γ(λ0|c0,d0) (30) 为了保证获得广泛的超先验,一般假设c0→0,d0→0,例如取c0=1×10-4,d0=1×10-4。 稀疏支撑集A=[a1,a2,…,aK]的各列独立,且假设服从复高斯先验分布,即 (31) 式中:Λ=diag(λ),λ假设为NsNd维独立伽马分布,即 (32) 式中:超参数ρ=1×10-3。 字典失配误差Δfd和Δfs假设服从NsNd维均匀分布,即 Δfd~U([-rd/2,rd/2]NsNd) (33) Δfs~U([-rs/2,rs/2]NsNd) (34) 式中:rd和rs分别为离散字典的归一化多普勒频率间隔和归一化空间频率间隔。 由于后验分布p(A,Δfd,Δfs,λ0,λ|X)不能显式给出,将A当作隐变量,则其后验分布满足: (35) 式中: μk=λ0ΣΦHxk (36) Σ=(λ0ΦHΦ+Λ-1)-1 (37) 由式(35)可知,信号支撑集矩阵A的稀疏解与μk和Σ的稀疏解一一对应。计算μk和Σ的稀疏解需要对超参数Δfd,Δfs,λ0和λ进行估计。根据稀疏贝叶斯理论,超参数可以用最大后验方法估计,即最大化p(Δfd,Δfs,λ0,λ|X),由于p(X)与上述超参数无关,因此最大化p(Δfd,Δfs,λ0,λ|X)与最大化p(Δfd,Δfs,λ0,λ,X)=p(Δfd,Δfs,λ0,λ|X)p(X)等价,并且有 p(A,X,Δfd,Δfs,λ0,λ)= p(X|A,Δfd,Δfs,λ0)p(A|λ)p(λ)p(λ0)· p(Δfd)p(Δfs) (38) 利用EM方法迭代更新超参数λ和λ0,具体推导过程可参见文献[24],λ和λ0的更新方程分别为 n=1,2,…,NsNd (39) (40) tr{(Ψ+Fdiag(Δfd)+Gdiag(Δfs))Σ(Ψ+Fdiag(Δfd)+Gdiag(Δfs))H}= (Δfd)TP1Δfd-2V1Δfd+(Δfs)TP2Δfs-2V2Δfs+C (41) 式中:C为常数。 P1= (42) P2= (43) V1= (44) V2= (45) 最小化式(41)可得到Δfd和Δfs的估计值 2V1Δfd+(Δfs)TP2Δfs-2V2Δfs} (46) 式(46)分别对Δfd和Δfs的偏导数为零,则可以得到字典失配误差的更新,即 (47) (48) 通过式(21)获得字典失配误差补偿后的空时导向矢量字典Φ(Δfd,Δfs),并重复迭代λ、λ0、Δfd和Δfs的EM估计过程直至达到设置的估计精度。在兼顾超参数估计精度和迭代收敛速度的情况下,设置超参数误差预设值最大值1×10-3,最大迭代次数2 000次。 迭代完成后获得稀疏解A及字典失配误差,进而获得修正后的空时导向矢量字典Φ,并重构杂波协方差矩阵,即 (49) 通过式(49)获得CCM估计值后,杂波空时谱可以表示为 (50) 综上所述,字典失配情况下的稀疏贝叶斯学习杂波空时谱估计方法具体步骤如下: 步骤1根据式(12)初始化空时导向矢量字典Ψ。 步骤2根据式(21)构建失配字典动态模型。 根据式(36)和式(37)计算均值μk和方差Σ。 根据式(39)、式(40)、式(47)和式(48)更新超参数λ、λ0、Δfd和Δfs。 判断误差是否达到预设值或迭代次数是否达到最大值,不满足则重复步骤2。 步骤3根据式(49)估计杂波协方差矩阵,然后根据式(50)计算杂波空时谱。 为了验证本文方法的有效性,通过如下参数生成仿真数据。雷达工作频率fo=450 MHz,载机平台高度H=9 000 m,阵元数M=8,相干脉冲数N=8,脉冲重复频率fr=300 Hz,360个杂波单元在0°~180°均匀分布,杂噪比CNR=40 dB, 从距离R0=15 km处开始仿真3个距离单元的杂波数据,距离分辨率为37.5 m。实验对比了本文方法和使用固定离散字典稀疏贝叶斯学习的SBL-STAP方法[18]。SBL-STAP方法中最大迭代次数为1 000次,正则化参数初始值取1×10-2,超参数修剪阈值取1×10-4。 实验1为了比较不同偏航角情况(有无字典失配问题)对稀疏恢复STAP的影响,阵列采用正侧视模式。折叠系数β=1,即杂波脊的斜率为1,对应载机运动速度vp=50 m/s。空时导向矢量字典网格划分系数ρs=ρd=4,即归一化空间频率和归一化多普勒频率都被等间隔分为32份,这时杂波脊正好落在空时导向矢量字典网格点上,不存在字典失配的问题。图3为真实杂波谱及上述两种方法使用相同的3个杂波样本进行稀疏恢复得到的杂波谱,可以看出当不存在字典失配时,SBL-STAP方法和本文方法形成的杂波谱均集中在杂波脊上,无明显展宽,具有较好的杂波抑制性能。 图3 不存在字典失配问题时的杂波谱估计 实验2阵列采用正侧视模式,折叠系数为β=0.8,即杂波脊的斜率为0.8,对应载机运动速度vp=40 m/s。空时导向矢量字典网格仍为实验1中ρs=ρd=4的等间隔划分,由于杂波脊斜率与字典网格不匹配,杂波脊不能完全落在空时导向矢量字典网格上,此时存在字典失配问题,如图4(a)所示。从图4(b)中可以看出, SBL-STAP方法恢复的杂波谱有明显的展宽,分辨率不高,杂波抑制性能损失较大。由实验1和实验2的结果对比可以看出,这种杂波谱展宽的情况主要是由空时导向矢量字典失配造成的,说明字典网格失配会使得稀疏恢复性能明显下降,STAP处理效果较差。而本文提出的基于动态字典的稀疏贝叶斯学习空时自适应处理方法,利用动态字典实现字典失配误差的估计补偿,能够形成较为清晰的杂波脊、连续性和展宽情况都获得了比较理想的结果,如图4(c)所示。 图4 存在字典失配问题时的杂波谱估计(正侧视阵,β=0.8) 实验3阵列采用非正侧视阵,φ=30°,载机运动速度vp=50 m/s真实杂波如图5(a)所示。从图5(b)可以看出SBL-STAP方法恢复得到的杂波谱中杂波脊较实验2中情况更为模糊,这主要是由于非正侧视阵的杂波脊为椭圆形,存在更多不能落在空时平面网格点上的杂波单元,由于字典失配问题的影响,稀疏恢复得到的杂波谱误差较大。而如图5(c)所示,本文方法获得的杂波谱仍然能够形成较为清晰的杂波脊,在非正侧视阵存在字典失配的情况下较SBL-STAP方法有较大的优势。 除上述杂波谱恢复情况分析外,STAP处理的杂波抑制效果通常使用信杂噪比损失(Signal to Clutter plus Noise Ratio Loss, SCNRLoss)来衡量[26],即 (51) 式中: (52) 图6为进行100次Monte Carlo实验得到的平均结果。其中图6(a)为正侧视阵情况,折叠系数β=0.8存在字典失配情况下的信杂噪比损失。图中OPT对应曲线表示利用CCM真实值进行STAP处理获得的信杂噪比损失,称为最优情况。可以看出本文方法形成了较窄的零陷,在抑制杂波的同时,能够获得较好的运动目标检测性能,除了在主杂波区形成零陷外,其他区域的SCNRLoss均较小,仅比最优情况低2 dB左右。而SBL-STAP方法形成的零陷较宽,这会使得更多与杂波多普勒频率接近的运动目标被当作杂波抑制掉,大大降低系统的运动目标检测性能。图6(b)为非正侧视阵,φ=30°存在字典失配的情况下的信杂噪比损失。可以看到与图6(a)相似的结果,本文方法主杂波区形成较窄的零陷,在抑制杂波的同时,能够获得较好的运动目标检测性能。而使用固定离散字典的SBL-STAP方法形成的杂波抑制区域较宽,对于运动目标的检测性能下降较为严重。 图6 字典失配情况下的信杂噪比损失 稀疏恢复STAP方法受字典失配影响较大,杂波抑制性能下降明显。本文提出了一种利用空时二维动态字典对失配字典误差进行估计补偿的稀疏贝叶斯学习空时谱估计算法,实现了存在字典失配情况下的杂波谱有效恢复,能够有效提高机载雷达杂波抑制性能。仿真实验表明,本文方法在存在字典失配的情况下,可以有效恢复杂波协方差矩阵,提高杂波抑制效果,其性能优于固定离散字典的SBL-STAP方法。1 信号模型
2 空时功率谱稀疏恢复及字典失配问题
2.1 空时功率谱稀疏恢复


2.2 字典失配问题

3 字典失配情况下稀疏贝叶斯学习空时谱估计
3.1 空时二维动态字典模型
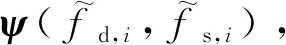
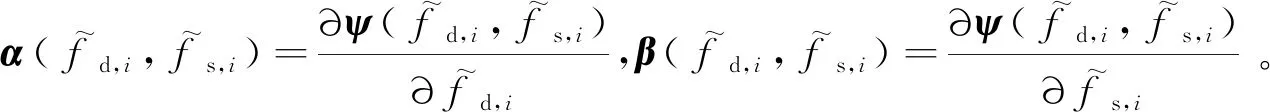
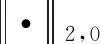
3.2 字典失配误差估计及空时谱稀疏恢复



4 仿真实验
4.1 杂波空时功率谱恢复效果比较


4.2 杂波抑制性能比较
5 结 论
