多太阳能无人机覆盖路径优化方法

2021-07-07杜楠楠陈建马奔王术波张自超

航空学报 2021年6期

杜楠楠，陈建，马奔，王术波, 3，张自超

1. 中国农业大学工学院，北京 100083

2. 北京航空航天大学自动化科学与电气工程学院，北京 100191

3. 武汉大学测绘遥感信息工程国家重点实验室，武汉 430079

近年来，随着无人机及其相关技术的发展，无人机已经广泛应用于国防军事[1]、灾后搜救[2]以及遥感[3-4]等领域。随着太阳能电池效率的提高，环保、可以实现长距离航行、并且能够执行多种任务的太阳能无人机进入了人们的视野[5]。1974年，第1架太阳能无人机“Sunrise I”试飞成功[6]。2003年，瑞士苏黎世联邦理工大学开始研制小型无人机“Sky-Sailor”，并于2008年6月在瑞士完成了27 h的低空飞行[7]。2005年，美国AC公司成功测试了主要应用于民用遥感测绘的电动滑翔太阳能无人机“SoLong”[8]。2017年，同样是由瑞士苏黎世联邦理工大学研发的太阳能无人机“Atlantik Solar”以连续飞行81.5 h打破了轻小型太阳能无人机的航时记录[9-10]。

无人机作业中最重要的问题之一是路径规划。传统的路径规划是点对点的，即规划出无人机和终点之间的一条路径[11]。在某些特定情况下，无人机需要获得某一区域的全面信息，或在该地区进行全覆盖作业，因此需要进行覆盖路径规划。“牛耕法”是一种典型的覆盖路径规划方法，即通过往复的直线运动来将区域覆盖完全[12]。在“牛耕法”中，一般选择使转弯次数最小的方向作为覆盖飞行方向[13-14]。对于不含障碍物的凸多边形区域，Gustavo等提出了基于车辆路径规划问题的、以作业时间最短为求解目标的多无人机覆盖路径规划模型，并在该问题中考虑了无人机的起飞操作时间对总作业时间的影响[13]。对于存在障碍物的区域，Latombe首先提出了梯形分割法，即通过和覆盖方向平行的割线首先将区域分为多个含障碍物或不含障碍物的子区域，再对每个不含障碍物的子区域进行牛耕式覆盖[15]。之后，Choset提出了Boustrophedon细胞分解方法[16]，该方法可将区域分割为面积更小的单元。之后，Huang提出了一种分解区域的割线可变的“基于线扫描的分解方法”，该方法可将区域分为数量更少的子区域[17]。在此基础上，陈海等考虑了无人机的转向时间较长，通过最小化覆盖作业的转弯次数来确定覆盖方向[18]。此外，Nedjati等首先将整个区域分为需要覆盖、不需要覆盖和无人机准备起飞的区域，之后再将整个区域划分为均匀网格，最终求解出一条覆盖所有不含障碍物的网格路径[19]。

在覆盖作业中，传统的电动无人机存在续航时间短的缺点，针对该问题，本文提出了应用多架太阳能无人机的覆盖路径规划问题。之后，基于文献[13]中针对凸多边形区域的覆盖路径规划模型，提出针对凹多边形以及内部含障碍物的待覆盖区域、以总作业时间和能量利用情况作为优化目标、基于无向图搜索的覆盖路径优化模型，通过定义约束方程来求解每架无人机的最优或相对最优的覆盖飞行方向和飞行路径。在实际应用无人机进行覆盖作业的任务中，一般以总作业时间为优化目标。例如在应用无人机植保作业中，越短的作业时间意味着越高的作业效率，同时意味着更高的经济效益。而在应用太阳能无人机作业中，还需要考虑对太阳能的利用情况，当无人机机载设备耗能较大时，需要同时考虑能量利用情况和总作业时间这2个优化目标，通过2个优化目标在具体任务中的重要性占比来确定各自的优化权重。本文创新点可总结如下：

1) 针对边界存在障碍物的凹多边形区域或内部含障碍物的多边形区域，提出基于无向图搜索的覆盖路径优化模型，以总作业完成时间最短为优化目标，通过定义约束条件来求解无人机的最优飞行路径。

2) 将总作业完成时间最短和能量流动效率最高同时作为优化目标，建立双目标优化方程。基于总作业完成时间最短，通过有限遍历的方式来求解在2个优化目标的权重系数不同时，使作业时间和能流效率相对最优的覆盖飞行方向和飞行路径。

1 太阳能无人机能量模型的建立

对于固定翼无人机来说，无人机机翼上方覆盖有太阳能电池板，将吸收来的太阳能转化为电能。应用太阳能无人机作业时，最重要的问题之一就是太阳能无人机的能量模型对作业效果的影响。本节在文献[20]的基础上建立了太阳能无人机的能量模型，进一步提出能量流动效率这一评价指标。

1.1 能量输入模型

已有太阳辐射模型主要分为两种：一种是考虑气象条件的全球辐射模型；一种是不考虑天气影响的晴空辐射模型。由于前一种模型的计算需要具备多种气象参数、计算复杂且准确度低，因此本文选择晴空辐射模型。在晴空辐射模型中，有ASHRAE、Badescu、Bashasu等模型，其区别在于模型的输入参数不同。其中，ASHRAE晴空辐射模型的相关参数齐全、计算相对简单且精度较高，该模型最受全球研究工作者的认可[20]。因此本文选择ASHRAE晴空辐射模型来建立太阳能无人机的能量输入估计模型。

太阳能电池板表面吸收的太阳辐射强度I与太阳光线在机翼表面的入射角呈线性关系。可计算出垂直于水平面的太阳辐射，即

(1)

式中：太阳常数I0=1 353(±21) W/m2[21]；nday为从1月1日开始算起的太阳天数。

进一步可以计算出太阳能电池板水平面的单位面积所吸收的太阳直接辐射强度Ib和太阳直接散射强度Id，如式(2)～式(4)所示:

(2)

(3)

(4)

式中：b和d分别为直射和散射空气质量指数；τb和τd分别为直射和散射光学深度，可通过查表获得；mr为空气质量比；αe为太阳高度角。

建立能量输入模型，首先应建立太阳光线与无人机之间的位置关系，如图1所示。图1中：αs表示太阳方位角，是目标物体的北方向与太阳光线入射方向的顺时针夹角；αe表示太阳高度角，是地平面与太阳入射光线之间的夹角；λ表示太阳入射角，是太阳入射光线与翼面法线之间的夹角。由文献[22]可计算出某一时刻和地点的αs和αe，如式(5)～式(8)所示：

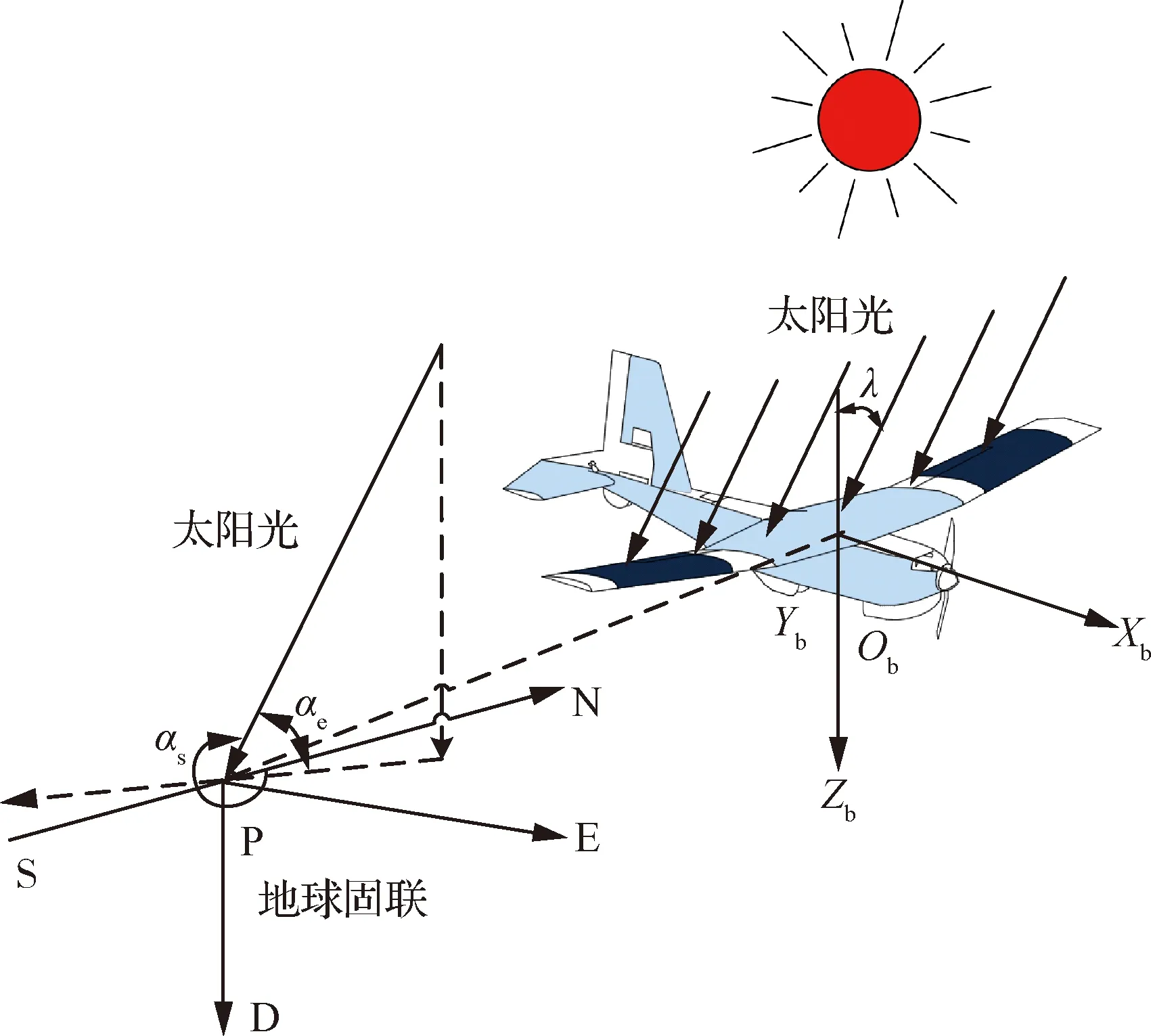
图1 太阳光线与无人机之间的位置关系

sinαe=sinnlatsinδ+cosnlatcosδcosω(t)

(5)

(6)

δ=0.409 3sin[2π(284+nday)/365]

(7)

ω(t)=0.261 8×(12-tlocal)

(8)

式中：nlat为作业地点的纬度；ω(t)为太阳时；δ为太阳赤纬角；tlocal为作业时刻。

进而计算太阳入射角λ，即

(9)

式中：Spb为太阳光线的单位向量在机体坐标系中的表示，即

(10)

式中：φ、θ、ψ分别为无人机的滚转角、俯仰角和偏航角；R(φ)、R(θ)、R(ψ)分别为在这3个方向的导航坐标系到机体坐标系的转移矩阵。

基于以上，可计算出太阳入射角的余弦，如式(11)所示：

cosλ=cosαesinαs(cosψsinφ-cosφ·

sinψsinθ)-cosαecosαs(sinφsinψ+

cosφcosψsinθ)+cosφsinαecosθ

(11)

根据ASHRAE晴空辐射模型，可计算单位机翼面积吸收的太阳辐射强度PS(λ)及太阳能无人机的能量输入功率Pin，即

(12)

Pin=ηsolSPS

(13)

式中：S为电池板的面积；ηsol为其光电转化效率。由此可计算出太阳能无人机在[t1,t2]时间内吸收的总能量，即太阳能无人机的输入能量Ein，即

(14)

1.2 能量输出模型

无人机的输出能量，主要指无人机克服空气阻力做功和机载作业消耗。可计算出无人机定高飞行时的能量输出功率Pout，即

(15)

式中：v为飞行速度；T为无人机螺旋桨拉力；ηprop为螺旋桨效率；PA为无人机机载作业消耗功率。由于无人机定高飞行时重力mg与升力L相等，因此可求出飞行速度v，如式(16)～式(18)所示：

Lcosφ=mg

(16)

(17)

(18)

式中：CL0为零升力系数；CLα为斜线升力系数；ρ为空气密度；α为无人机的迎角。进而可计算出螺旋桨的拉力T，如式(19)～式(21)所示：

T=D

(19)

(20)

(21)

式中：Ra为无人机的展弦比；CD为飞行阻力系数；K为空气动力系数；ε为奥斯瓦尔德效率因子。

基于式(1)～式(21)，可以计算出无人机在[t1,t2]时间内的输出能量Eout，即

(22)

选择文献[7]中的“Sky-Sailor”太阳能无人机作为本文的无人机模型，其主要参数如表1所示。

表1 太阳能无人机模型参数

1.3 能量流动效率

为了表示太阳能无人机在飞行作业过程中对太阳能的利用率，本文提出能量流动效率ηflow这一评价指标，即

(23)

由式(23)可知，能量流动效率是无人机飞行消耗和机载作业消耗的总能量与吸收的太阳能的比值。该值的大小体现了太阳能无人机是否及时有效地将吸收来的太阳能转化为作业或飞行消耗所用的能量。由式(23)可知，能量流动效率ηflow必然小于1，并且该值越大，在飞行作业过程中对太阳能的利用率越高。此外，对于同一架太阳能无人机，能量流动效率越高，意味着电池的负载对于该作业来说越小；反而当能量流动效率过低时，电池的负载对于该作业任务来说则是一种“负担”。因此在基于太阳能无人机的覆盖路径规划问题中，可在以覆盖作业时间为优化目标的基础上，将能量流动效率同时作为优化目标来求解无人机的飞行路径。

2 含障碍区域覆盖路径单目标优化

在无人机覆盖作业中，最主要的优化目标是覆盖作业时间。因此本节研究的问题是，有M架相同的无人机需要覆盖一个边界存在障碍物的凹多边形区域或内部含障碍物的多边形区域。假设无人机的飞行高度恒定，不考虑续航时间对作业时间的限制。需要求解的是当以总作业完成时间最短为优化目标时每架无人机的最优路径。为解决该问题，则需建立针对含障碍物区域的覆盖路径优化模型。

2.1 覆盖飞行方向的确定

本文基于牛耕法进行覆盖路径规划，因此首先需要确定覆盖飞行方向。为保证覆盖作业的质量，无人机常需要飞出区域进行转弯，因此转弯次数的增加往往对应着总路径长度的增加[13]。为了减少无人机作业时间则应尽量减少无人机的转弯次数。由于仅考虑总作业完成时间这一优化目标，因此选择能使转弯次数最少的方向作为最佳覆盖飞行方向。

首先定义一组坐标点来表示含障碍物待覆盖区域的边界，假设该组坐标点的集合为B={bk=(xk,yk),k=1,2,…,n}。进一步可以得到待覆盖区域的边集为L={lk=[(y-yk)(xk-xk+1)=(x-xk)(yk-yk+1),x∈(xk,xk+1),k=1,2,…,n]}。由于待覆盖区域为凹多边形或内部含障碍物，因此将边集L分为凹边或内部障碍物边界集合L1={lk,k=1,2,…,h}和凸边或外部非障碍物边界集合L2={lk,k=1,2,…,n-h}，如图2所示。

图2 待覆盖区域边集的划分

在凸多边形区域中，垂直于多边形最小宽度的方向是转弯次数最少的方向[14]。而当待覆盖区域存在凹边或内部含有障碍物时，由于无人机在凹边处或障碍物边界处也需要转弯，因此转弯次数不仅和待覆盖区域宽度有关，还与凹边或障碍物的位置和形状有关。

因此，针对含障碍物区域的最佳覆盖飞行方向的选取原则如下。首先在无人机的覆盖作业宽度确定之后，用一组间距为单架无人机覆盖作业宽度的平行直线以不同的角度与待覆盖区域相交，通过遍历的方式找到相交节点数量最小的角度范围。之后再在这组角度范围中选取出待覆盖区域最小宽度方向的垂直方向，作为无人机的最佳覆盖飞行方向。其中，最小宽度方向是指间距最短的包容该多边形的平行线的方向。覆盖飞行方向的确定过程如图3所示，其中无人机的最佳覆盖飞行方向如图中箭头所示。

图3 覆盖飞行方向的确定

一旦覆盖飞行方向被确定，就可以对待覆盖区域进行行划分，为后续的覆盖任务分配做准备。这里假设在最佳覆盖飞行方向的垂直方向上，待覆盖区域的宽度为h，假设单架无人机的覆盖作业宽度为L，进而可求得覆盖作业的行数Nl，即

(24)

式中：为保证对待覆盖区域的完全覆盖，即两个覆盖行之间不存在未经覆盖的空白区域，因此对Nl进行向上取整。之后修正每一行的实际覆盖宽度dl，即

(25)

2.2 覆盖路径优化模型

在覆盖作业的基本条件被确定之后，基于文献[13]提出的针对凸多边形待覆盖区域的覆盖路径规划模型，建立本文中针对含障碍物区域的基于无向图搜索方法的覆盖路径优化模型。首先，用一组平行且间距为dl的直线沿着最佳覆盖飞行方向与待覆盖区域边界相交，得到一组交点P={pi=(xi,yi),i=1,2,…,N-1}。之后这组交点和无人机的起飞节点共同组成无向图G=(V,E)中的节点集合V，如图4所示。

图4 无向图节点的确定

之后，对该集合中的每个节点编号，所有节点的数量为N。其中无人机起飞节点的编号为1，与第1个覆盖行相关的节点编号为2和3，与第2个覆盖行相关的节点编号为4和5，以此类推。最终每个覆盖行都与其对应的偶数和奇数节点相关。无向图G=(V,E)中的边集E由两两连接图中的N个节点的所有线段组成，从而形成一个完整的无向图。

在数学上，无向图G可以用N×N的成本矩阵C来表示，其中元素Cij表示节点i和节点j之间的欧几里得距离。无向图G中的边集表示为E={lij=[(y-yi)(xi-xj)=(x-xi)(yi-yj),x∈(xi,xj)],i,j=1,2,…,N}。假设凹边及内部障碍物区域由于存在障碍物而无法穿越，因此与凹边及障碍物边界相交的路径将不被选取。为方便后续约束方程的定义，此处将成本矩阵中表示与凹边相交的边的元素置为零，即

if ∃ ∀(xa,ya),

xa∈(xk,xk+1)∪(xi,xj),

(ya-yk)(xk-xk+1)=(xa-xk)(yk-yk+1),

xa∈(xk,xk+1),k=1,2,…,n;

(ya-yi)(xi-xj)=(xa-xi)(yi-yj),

xa∈(xi,xj),i,j=1,2,…,N,Cij=0

(26)

将无向图中和凹边及内部障碍物边界相交的边去除后，可将针对凹多边形或内部含障碍物的多边形区域的覆盖路径优化模型的无向图表示如图5所示。

图5 表示含障碍区域覆盖路径优化问题的无向图

在基于无向图搜索的覆盖路径优化模型中，位于起飞节点处的多架无人机的任务是遍历划分为行的待覆盖区域，进一步可以将该任务描述为每架无人机须对无向图中的边进行搜索，保证其沿着覆盖飞行方向访问无向图中的所有节点，即必须访问无向图中所有表示待覆盖行的边。假设覆盖任务为无人机遥感作业，并且假设采用几何遥感模型。根据相机的成像原理，单架无人机的遥感区域可建模为矩形或梯形[14]。因此，在本文中，单架无人机的覆盖宽度即在覆盖飞行方向的垂直方向上的遥感矩形的宽度。由上可知，在本文的覆盖作业中，该覆盖路径优化模型能保证无人机覆盖每一个待覆盖行，并在覆盖行和边界相交的节点处转弯，因此能保证对待覆盖区域的完全覆盖。

根据优化目标来定义目标方程，并通过定义约束条件来强制无人机在路线中按照一定规则飞行，最终保证每个待覆盖行都有一架无人机“负责”。通过求解表示该优化问题的方程组，最终可得到每架无人机访问节点的最佳顺序，即每架无人机的最优路线，该求解过程如图6所示。

图6 针对含障碍区域的无向图搜索方法的求解示意图

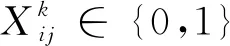
基于以上变量的定义，可求出第k架无人机的作业时间Tk，即

(27)

在本节中，将总作业完成时间最短这一单一目标作为优化目标，即飞行路径最长的无人机的作业时间最短。进而，该优化问题的目标方程可以表示为

min(max(Tk))

(28)

如式(28)所示，该目标函数可表示为一个线性的min-max问题。下面通过定义约束方程，来限制无人机按照一定的规则飞行。

约束1式(29)中的约束条件表示除起飞节点外的每个节点只能被一架无人机访问一次。

(29)

约束2式(30)中的约束条件保证了到达某个节点的无人机和离开该节点的无人机是同一架。

p=2,3,…,N；k=1,2,…,m

(30)

约束3为了强制每架无人机在起飞节点1处起飞，并回到起飞节点，确保该路径中没有内部子循环路径，式(31)表示了标准的子循环消除约束。

ui,uj∈Z;i,j=2,3,…,N

(31)

式中：ui和uj代表任意实数[23]。

约束4为了保证无人机能够按照最佳覆盖方向飞行，确保每一个覆盖行都能被无人机覆盖，还需要定义约束方程：

i=2,4,…,N

(32)

式(32)的约束条件保证了访问某一个覆盖行，其中一个节点的无人机必将访问该覆盖行的另一个节点。考虑到节点的编号顺序，该约束条件通过强制访问某个偶数节点的无人机必须访问其对应的下一个奇数节点以及访问某个奇数节点的无人机必须访问其对应的上一个偶数节点来实现。因此，该约束对于使该方法成为解决覆盖路径优化问题的可行方案来说是至关重要的。

约束5为了避免无人机沿着与覆盖方向不平行的边穿过待覆盖区域，防止无人机急转弯，则需要在优化模型中添加两个可选的约束，即

i=2,4,6,…,N

(33)

i=3,5,7,…,N

(34)

在针对含障碍区域的覆盖路径优化模型中，为了使问题尽量有解，即路径不会陷在凹边或者障碍物边界处，约束5有时不需要添加进来。如图7，当添加了该约束条件后，无人机只能沿着与凹边或障碍物边界相交的边l35、l37、l39飞行，因此问题就会变得无解。当不添加此约束时，无人机则可从节点3沿着l36、l38飞至节点6或8，从而飞出凹边或障碍物边界区域。当然无解只可能出现在待覆盖行数量极少的情况下，而当待覆盖行数量较多时，可选择添加该约束条件。对于该约束条件对覆盖路径求解的影响将在2.3节中通过对比实验来说明。

图7 是否添加约束5对路径求解的影响

约束6为了保证无人机不沿着穿越凹边或障碍物边界的路径飞行，需要添加约束方程：

(35)

通过求解式(28)中的目标函数和式(29)～式(35)中的约束方程，即可求解出给定数量的无人机在最短的时间内遍历建模为无向图G的待覆盖区域的最优路径。

此外，目标函数(28)的求解目标是使得多架无人机中最长路径的那架无人机的路径最短，因此，一旦找到最长的无人机路径，就无法保证其他无人机的路径也最小化。为了保证所有无人机的路径长度都最小，采用迭代的解决方案，通过多次迭代来保证每架无人机的路径最优。首先，在第1次迭代中，使用原始的无向图G，解决的优化问题正是前面提出的问题。在第2次迭代中，首先移除在第1次迭代中分配给最长路径的无人机以及除起飞节点外所有属于该路径的节点和边。更新参数之后，再用第1次迭代中的方法求解。以此类推，直至所有节点都被遍历。通过迭代的方法，可以保证每架无人机的路径都是最优的，即在目标函数不变的前提下，最大可能地将覆盖任务的总成本降到最低。该覆盖路径优化模型的算法流程如图8所示。

图8 覆盖路径优化模型的算法流程图

2.3 仿真实验

本文中的仿真实验在运行内存为4 GB RAM、CPU为Intel Core i3的计算机的MATLAB 2018b中进行，并通过Yalmip工具箱求解。

首先假设作业地点为(125°E,50°N)，作业时间为2020年5月1日上午09：00。假设无人机的覆盖作业宽度为L=130 m。当无人机攻角α=2°时，可求得其速度为v=10.778 4 m/s。

针对凹多边形区域和内部含障碍物的多边形区域，根据待覆盖区域的形状分别将实验分为两组，每组中假设可用的无人机数量m分别为2架、3架两种情况。仿真得到每种情况下的最佳覆盖方向δ、修正后的覆盖宽度dl、每架无人机的作业时间Tk以及总作业完成时间t。之后根据太阳能无人机的能量模型计算出其能量输入功率Pin、能量输出功率Pout，进而求出该覆盖作业中的能量流动效率ηflow，用来评价太阳能无人机在该覆盖作业中对能量的利用率。

2.3.1 针对凹多边形区域

在本节的第1组实验中，定义待覆盖作业区域边界的坐标分别为(-2 555,-986)、(-2 770,-99)、(341,-49)、(345,-961)、(-833,-1 073)、(-1 754,-683)、(2 074,-895) m，无人机起飞节点的坐标为(-3 335,-289) m。

当无人机数量分别为m=2，3时，每架无人机的最优路径如图9所示。

图9 每架无人机的最优路径(凹多边形区域，第1组实验)

由仿真求解可得，在该组实验下，无人机的最佳覆盖飞行方向为δ=1.55 rad，修正后的覆盖宽度为dl=125.96 m。当无人机数量不同时，每架无人机的作业时间和总作业完成时间如表2所示。

表2 每架无人机的作业时间和总作业完成时间(凹多边形区域，第1组实验)

在本节的第2组实验中，定义待覆盖作业区域边界的坐标分别为(-2 707,-1 152)、(-2 702,-38)、 (440,119)、(553,-932)、(-279,-1 111)、(-969,-1 140)、(-986,-791)、(-1 592,-433)、 (-2 071,-475)、(-2 058,-1152) m，无人机起飞节点的坐标为(-3 334,-47) m。

当无人机数量分别为m=2，3时，每架无人机的最优路径如图10所示。

图10 第架无人机的最优路径(凹多边形区域，第2组实验)

由仿真求解可得，在该组实验下，无人机的最佳覆盖飞行方向为δ=1.52 rad，修正后的覆盖宽度为dl=119.83 m。当无人机数量不同时，每架无人机的作业时间和总作业完成时间如表3所示。

表3 每架无人机的作业时间和总作业完成时间(凹多边形区域，第2组实验)

2.3.2 针对内部含障碍物区域

在本节的第1组实验中，定义待覆盖作业区域外边界的坐标分别为(-2 780,-1 495)、(-2 780,-305)、(-550,-305)、(-550,-1 495) m，定义待覆盖区域内障碍物边界的坐标为(-2 283, -958)、(-2 210,-525)、(-1 838,-482)、 (-1 799,-910) m，无人机起飞节点的坐标为(-3 424,-300) m。

当无人机数量分别为m=2，3时，每架无人机的最优路径如图11所示。

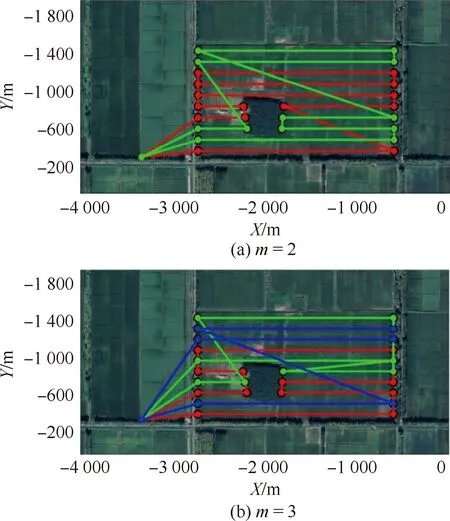
图11 每架无人机的最优路径(含障碍物区域，第1组实验)

由仿真求解可得，在该组实验中，无人机的最佳覆盖飞行方向为δ=1.57 rad，修正后的覆盖宽度为dl=119 m。当无人机数量不同时，每架无人机的作业时间和总作业完成时间如表4所示。

表4 每架无人机的作业时间和总作业完成时间(含障碍物区域，第1组实验)

在本节的第2组实验中，定义待覆盖作业区域边界的坐标分别为(-2 204,-170)、(-533,-1 227)、(92,-453)、(11,-283)、(72,76)、(-1 691, 390) m，定义待覆盖区域内障碍物边界的坐标为(-1 118,-642)、(-1 260,-626)、(-1 352,-497)、(-1 304,-364)、(-961, -299)、(-921,-396) m，无人机起飞节点的坐标为(641,-5) m。

当无人机数量分别为m=2，3时，每架无人机的最优路径如图12所示。

图12 每架无人机的最优路径(含障碍物区域,第2组实验)

由仿真求解可得，在该组实验中，无人机的最佳覆盖飞行方向为δ=1.75 rad，修正后的覆盖宽度为dl=124.38 m。当无人机数量不同时，每架无人机的作业时间和总作业完成时间如表5所示。

表5 每架无人机的作业时间和总作业完成时间(含障碍物区域,第2组实验)

在针对含障碍物区域的多智能体覆盖路径规划问题中，文献[24]提出一种多农机编队的基于旋转光束与改进概率路线图的路径覆盖算法。在该方法中，3架农机组成倒“V”形编队，等效成一架农机后进行覆盖作业。针对含障碍物待覆盖区域的第1组和第2组实验，实验条件相同，应用该算法的实验结果如图13所示。

由图13可看出，采用编队作业进行覆盖路径规划时，路径中多次出现重复飞行的路径，导致总飞行路径增加。该方法与本文方法在作业时间上的对比如表6所示。其中，t1表示应用文献[24]中方法的作业时间，t2表示应用本文方法的作业时间，a表示[(t2-t1)/t1]×100%，即本文方法在作业时间上提高的百分比。

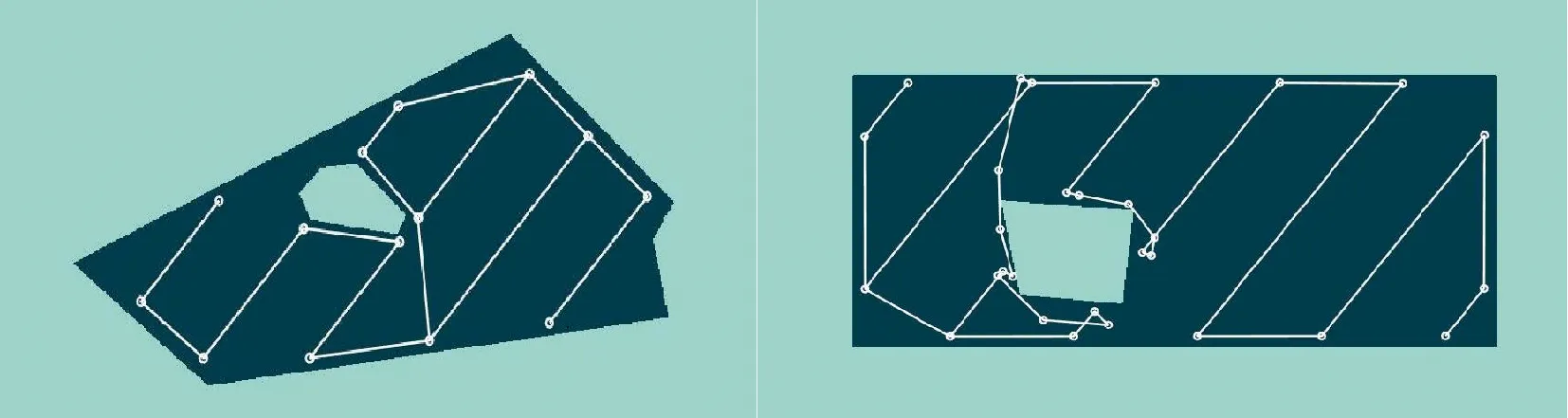
图13 其他覆盖路径规划算法的对比实验结果

表6 在覆盖作业时间上的对比实验结果

由表6可以看出，本文方法在路径规划时间上较文献[24]中的方法提高了10%以上，且文献[24]中的方法没有考虑智能体往返于出发点的路径长度。因此由仿真实验可看出，本文采用多无人机分散作业且基于无向图搜索的覆盖路径优化模型可行且较优。

最后，假设本文中用于覆盖作业的无人机的机载作业消耗功率为PA=60 W，可计算出每架太阳能无人机的能量输入功率Pin和输出功率Pout为

Pin=72.462 6 W,Pout=68.305 7 W

根据Pin和Pout以及每架无人机的作业时间可求得作业中每架无人机的能量生产总值和能量消耗总值。进一步可计算出每架无人机的能量流动效率为

2.3.3 添加约束5的对比实验

当考虑添加约束5 时，无人机将不被允许沿着与覆盖行不平行的边飞行。此处选取内部含障碍物区域的第1组实验中无人机数量m=3的情况，分别添加和不添加约束5进行对比。图14为添加该约束条件的实验结果，表7为两种情况下每架无人机的作业时间和总作业完成时间的对比实验结果。

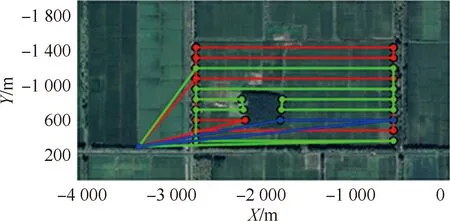
图14 添加约束5的对比实验

表7 添加约束5的对比实验结果

通过图11和图14的对比可以看出，未添加该约束条件的无人机路径中出现了3条与待覆盖行不平行的路径，而在添加该约束条件的实验中，无人机均沿着与覆盖行平行的方向飞行。根据表7 中的实验结果可以看出，当未添加该约束条件时，每架无人机的飞行作业时间比较平均，总作业完成时间也较短。而当添加了该约束条件时，为了使问题有解，每架无人机的路径长度不够平均，总作业完成时间也较长。

3 含障碍物区域考虑能流效率的覆盖路径双目标优化

当考虑无人机的姿态变化时，由于无人机转弯时的姿态变化会影响其能量输入和能量输出，进而影响能量流动效率的大小。因此在本节中针对含障碍物区域，考虑了无人机在飞行过程中的姿态变化，将总作业完成时间最短和总能量流动效率最高同时作为优化目标，在优化作业时间的基础上，通过有限遍历的方式找到使作业时间和能流效率相对最优的覆盖飞行方向和每架无人机的飞行路径。

3.1 转弯路径细化策略

无人机在平飞状态时姿态角保持不变，而在转弯状态时，需要调整滚转角来使无人机按照一定的转弯半径实现转弯飞行。若要考虑无人机在转弯时的姿态变化对最优路径规划的影响，则应首先确定无人机在不同情况下的转弯策略。

在本问题中有两种情况需要考虑：无人机在两个覆盖行之间转换的转弯路径；无人机从起飞节点飞至第一个节点后或从最后一个节点返回至起飞节点前的转弯路径。在转弯半径确定的前提下，以总路径长度最短为原则来确定最佳的转弯路径。首先讨论无人机在两个覆盖行之间转换时转弯路径的细化。

首先假设无人机转弯细化之前的路径如图15 所示。其中两节点之间的距离为dAB，两覆盖行之间的距离为d，无人机的转弯半径为R，图中箭头的方向表示其飞行方向。

图15 无人机转弯细化前的路径

由文献[25]可知，无人机的最佳转弯策略需要根据其转弯半径R、两行之间的间距d以及转弯处的折线AB与覆盖行L1之间的夹角β来进行分类讨论，每种情况下最优的路径如图16所示。

图16 覆盖行之间的最优转弯策略

之后考虑无人机从起飞节点飞至第一个节点后或从最后一个节点返回至起飞节点前的转弯路径细化策略。分别考虑起飞节点到第一个/最后一个节点之间的连线与待覆盖行之间的角度为锐角和钝角的两种情况。为保证覆盖作业的覆盖率并尽量使路径最短，设计最佳飞行路径如图17所示。

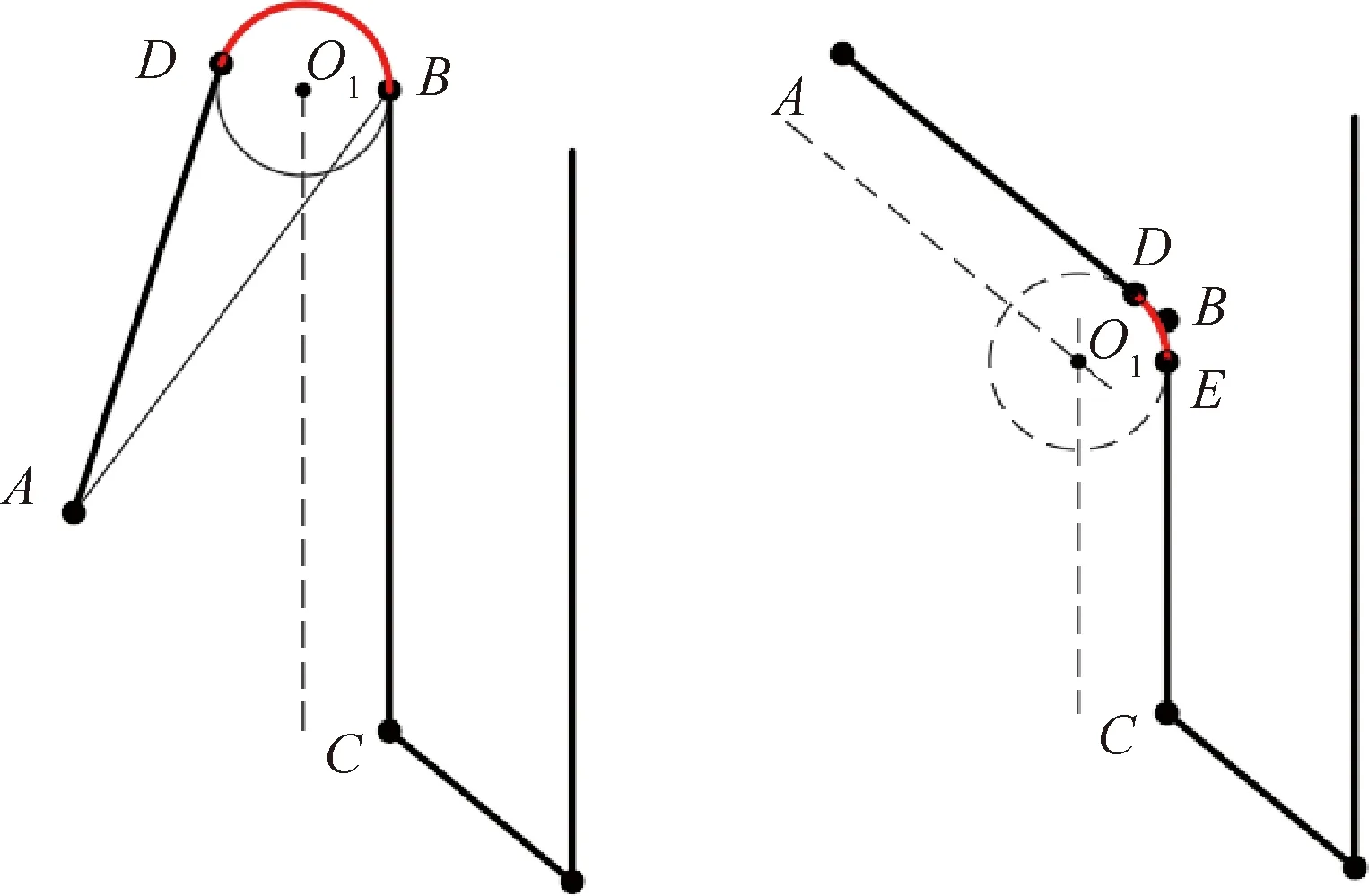
图17 起点与覆盖行之间的最优转弯策略

由文献[25]，可计算出无人机转弯半径R，即

(36)

由文献[26]可知，固定翼无人机滚转角的安全范围为-π/4～π/4 rad，即滚转角最大φmax=π/4 rad。当滚转角取得最大值时，R=Rmin。进而由式(36)可计算出最小转弯半径为Rmin=7.15 m。

3.2 覆盖路径优化模型

无人机在转弯时，滚转角会发生变化，该角度会影响无人机的能量流动效率。当将能量流动效率同样作为优化目标时，不同的转弯路径占比则会影响能量流动效率的大小，而当选择不同的覆盖飞行方向时，转弯路径的占比将发生变化。在本节中，将以能量流动效率最高和总作业完成时间最短同时作为双优化目标来求解相对最优的覆盖飞行方向和每架无人机的飞行路径。首先给出双目标优化方程为

k1+k2=1

(37)

式中：k1、k2为总作业完成时间和总能量流动效率在优化方程中的权重系数。可根据总作业完成时间和总能量流动效率在作业任务中的重要性占比来确定k1和k2的大小。例如当无人机数量较少且待覆盖区域面积较大时，可使总作业时间的权重系数更大，取k1>0.5；当无人机机载耗能较大时，可使总能量流动效率的权重系数更大，取k2>0.5。

由于无人机在平飞和转弯时的姿态不同，进而会导致其能量流动效率不同。假设无人机在转弯状态下的能量输入和能量输出功率为Pin1和Pout1；无人机在平飞状态下的能量输入和能量输出功率为Pin2和Pout2；无人机转弯飞行用时tt，非转弯飞行用时tnt，则可计算出当考虑无人机姿态变化时的能量流动效率ηflow，即

(38)

在覆盖路径双目标优化模型中，首先选取一定的角度为单位角度将覆盖飞行方向划分为有限种情况。在每种情况中，以时间最短为优化目标，求解出每架无人机的最优路径。之后细化无人机的转弯路径，计算出每种情况下的转弯用时和非转弯用时，进而计算出每种情况下的总作业完成时间和总能量流动效率。最后设置两种优化目标的权重系数，将每种情况下的总作业完成时间和总能量流动效率代入双目标优化方程中，求解出使作业时间和能流效率相对最优的覆盖飞行方向和飞行路径。由于遍历求解次数较少，因此这种通过有限遍历来优化的方式在工程上求解相对快速、可行性高。