交互式棱柱网格生成中翘曲现象形成机制及消除算法

2021-07-07孙岩江盟孟德虹庞宇飞

航空学报 2021年6期

孙岩，江盟，孟德虹，庞宇飞

中国空气动力研究与发展中心计算空气动力研究所，绵阳 621000

近几十年，伴随着计算机硬件与计算方法的快速发展，计算流体力学(Computational Fluid Dynamics, CFD)模拟能力迅速提升，已经能够在部分阶段代替试验手段，成为飞行器快速精细化设计的重要工具，从根本上改变航空航天飞行器的设计模式[1-2]。

目前主流CFD方法基于网格对计算区域进行空间离散，然后迭代求解离散后的代数方程得到流场的数值解，并通过表面积分获取飞行器的宏观气动载荷特性。因此，网格是开展CFD分析的前提和基础，直接影响流场数值模拟的精准度与效率[3]。

CFD计算网格按照相邻节点之间的拓扑关系可以分为结构网格和非结构网格两类[4]。结构网格内部节点的相邻节点数量是固定的，可以直接通过数组的索引序号来定义网格节点间的连接关系，而非结构网格内部节点的相邻节点数量是变化的，需要通过单独的数据结构对节点间的连接关系进行定义。相比于非结构网格，结构网格在效率、精度、分辨率和程序实现上均有明显的优势。但针对复杂的工程外形，结构网格生成十分困难，需要投入大量的人力开展结构网格的拓扑设计[5]。而随着计算机能力的快速提升，非结构网格相比结构网格的计算效率短板逐渐缩小，且在外形灵活性、生成速度方面的优势逐渐凸显，已经成为主流商业软件和部分in-house代码的首选网格类型[6]。

非结构网格单元类型主要有二维的三角形和三维的四面体，均可以实现任意离散区域的自动化填充，但在模拟梯度占主导的边界层流动时表现糟糕[7]。针对边界层流动问题，棱柱/四面体混合网格是目前CFD模拟中主要采用的解决方案，其中半结构化的棱柱网格能够弥补非结构三角形/四面体单元模拟黏性流动的不足，具有更好的流动分辨率。但复杂外形的棱柱网格生成仍然是具有挑战性的难题，是混合网格生成的核心和难点，已经成为网格生成领域的重要研究方向[8]。

目前，边界层棱柱网格主要沿着自动生成的方向发展，有不同的算法实现思路，例如各项异性四面体网格聚合[9-10]、法向推进[11-16]、Level Set界面追踪[17-19]以及求解PDE方程[20-21]，但不同算法思路的核心均是通过确定前沿推进单元的法矢和步长，构造棱柱网格单元。自动化棱柱网格生成方法具有较高的生成效率，人工参与少，但针对复杂外形，很难确定普适的控制参数，最终生成的棱柱网格难以避免较差质量单元的存在，且难以对局部网格单元质量进行调整和优化，影响整体CFD模拟的精度和效率[22]。

此外，还有研究者通过构造的思路人工交互生成棱柱网格，例如本文作者等发展的基于背景结构网格约束框架[23]、基于网格变形插值[24]的交互式棱柱网格生成技术，能够对局部棱柱网格质量进行有效调整，从而生成高质量的边界层棱柱网格。尤其是基于变形插值的棱柱网格生成方法，可以直接嵌入目前的主流网格生成软件中，对航空航天飞行器流动模拟具有潜在的工程应用价值。

但在进一步的算例测试中，基于变形思路的棱柱网格生成会在部分情况下产生翘曲现象，影响网格的质量，严重情况下会产生负体积单元，导致棱柱网格生成失败。因此，本文通过特定算例对棱柱网格生成中翘曲现象的形成机制进行研究，找出翘曲现象产生的原因，并探索相应的消除算法，改善交互式棱柱网格生成技术的鲁棒性。

1 交互式棱柱网格生成方法

交互式棱柱网格生成借鉴了网格变形的思路，将棱柱网格生成看成是物面网格连续变形的过程。图1展示了交互式棱柱网格的生成思路，首先生成物面网格边界棱线的空间推进面网格，然后利用三维空间插值方法将边界棱线网格点上的推进位移插值到内部网格点上，得到棱柱网格每一层网格点的坐标，最后组装获得整个棱柱网格。交互式棱柱网格生成中采用径向基函数实现边界棱线网格点位移到内部点位移的插值，基函数使用网格质量控制效果较好的Wendland’s C2型紧支函数，关于交互式棱柱网格生成的详细算法过程可以参考文献[24]。

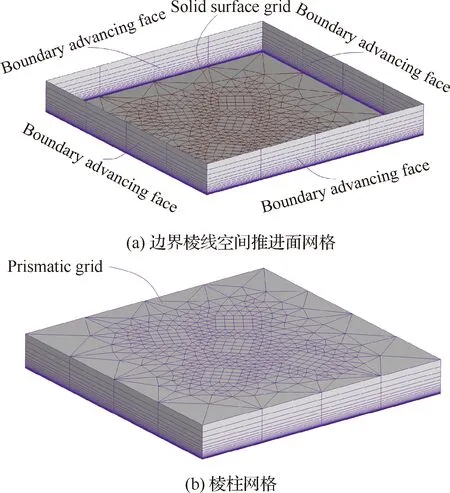
图1 交互式棱柱网格生成方法

2 翘曲现象

针对物面形状比较复杂的情况，例如曲率或外法矢变化剧烈的区域，基于径向基函数插值的交互式棱柱网格生成方法可能在局部位置形成翘曲现象，降低棱柱网格的质量，严重时可产生负体积网格单元，导致棱柱网格生成失败。本节通过典型航空外形的棱柱网格生成算例对这种局部区域产生的翘曲现象进行介绍和描述。

2.1 测试外形

选择德国宇航中心(DLR)设计的双引擎现代宽体运输机标模DLR-F6作为测试算例。DLR-F6模型被选为两届AIAA阻力预测会议DPWII、DPWIII的标准计算外形，用于评估世界范围内CFD软件的发展水平，具有十分广泛的影响力。图2给出了DLR-F6模型翼身组合体构型下的外形，采用下单翼的设计，机翼从机身的中下部穿出，形成一些复杂的交叉位置，给棱柱网格的生成带来一定挑战[25]。网格生成测试中采用DLR-F6风洞缩比模型的尺寸，翼展长度为1 173 mm，机身长度为1 192 mm，详细几何信息可见文献[26-27]。

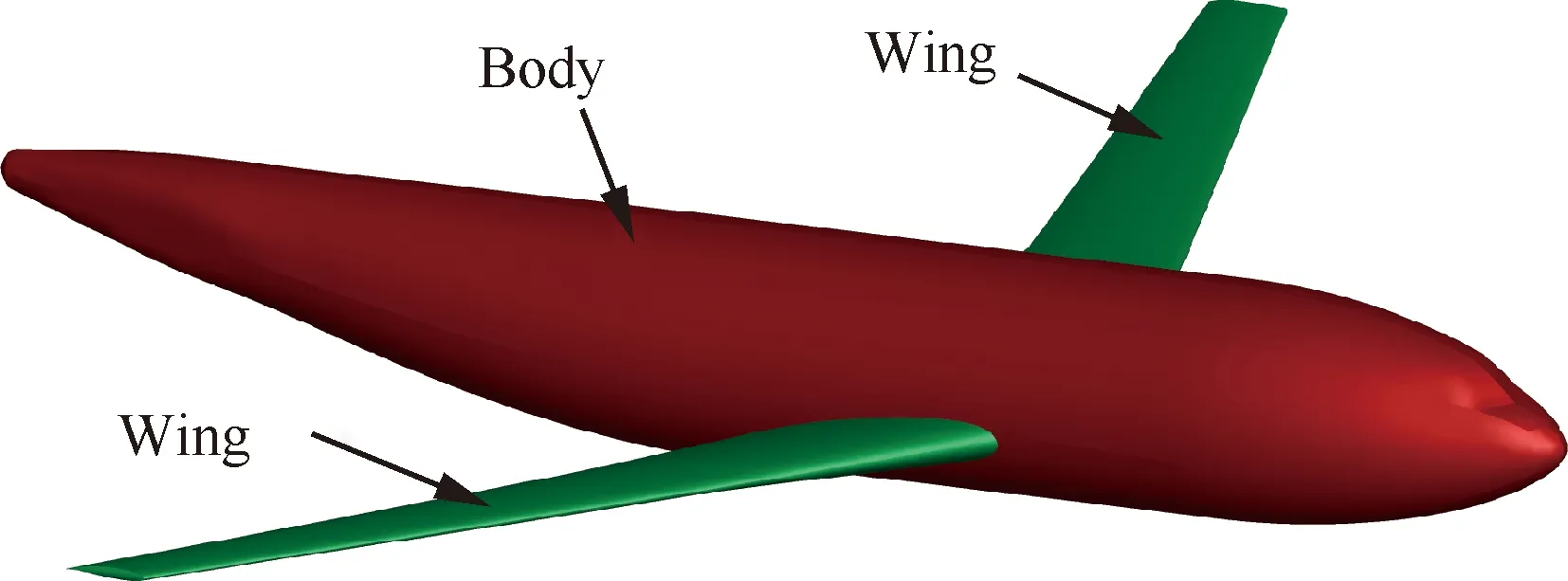
图2 DLR-F6翼身组合体构型[25]

2.2 棱柱网格生成

棱柱网格生成测试中发现翘曲现象主要发生在DLR-F6翼身组合体模型的机翼区域，机身位置翘曲不明显。为了更好地观察和分析翘曲现象，减少多余因素的干扰，本节采用DLR-F6模型的机翼开展棱柱网格生成的测试。

图3给出了DLR-F6模型机翼的表面网格，整个机翼表面依据前后缘区域分割成17个网格面，网格面由三角形和四边形单元混合而成，后缘为了保证推进后的棱柱网格质量，采用全四边形的单元。整个表面网格包含12 826个网格点，374个三角形单元，12 565个四边形单元。

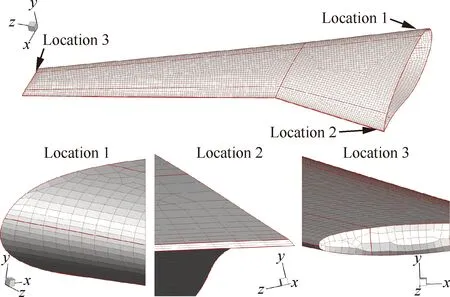
图3 DLR-F6模型机翼表面网格

棱柱网格生成测试通过中国空气动力研究与发展中心自主开发的棱柱网格生成程序PG2(Prismatic Grid Generation)开展。图4给出了生成后的DLR-F6机翼棱柱网格，其中第1层网格高度Δh设定为0.001 mm，网格高度法向增长比例为1.2，沿法向分布有39个网格点。可以看出，PG2能够成功生成机翼的棱柱网格，且外网格面比较规则，但在靠近前缘和后缘的位置产生了明显的条状翘曲，如图4(a)所示。选取翘曲明显的两个剖面z=217 mm、z=245 mm，可以发现，翘曲现象在前后缘附近的上下表面均有发生，后缘附近的翘曲更加明显，存在显著的凸起，而在远离前后缘的机翼中部位置，没有发生翘曲问题，如图4(b)和图4(c)所示。

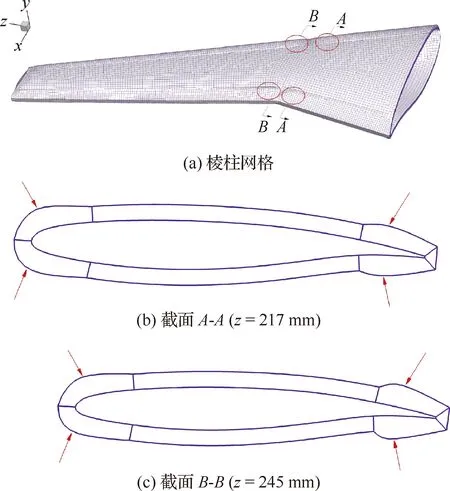
图4 DLR-F6机翼棱柱网格生成

图4的棱柱网格生成结果表明，在曲率或法矢变化明显的区域(机翼前后缘)容易发生翘曲现象，而在曲率或推进法矢变化缓慢的区域(远离前后缘的机翼中部)发生翘曲现象的可能性较小。

3 翘曲形成机制

基于径向基函数插值的交互式棱柱网格生成方法是使用物面边界网格点推进位移插值得到内部网格点的位移，然后组装得出整体的棱柱网格。当物面曲率或推进法矢急剧变化时，推进位移在某个坐标方向的分量可能会随着法矢的变化而剧烈改变，并通过径向基函数插值传递给内部网格点。因此猜测棱柱网格生成中的翘曲现象是由法矢变化导致的边界点推进位移分布不光滑引起的。

为了验证这一猜测，本节以平板外形棱柱网格生成为例，通过添加位移扰动的方式模拟曲率或法矢改变引起的位移变化，进一步分析棱柱网格翘曲现象的形成机制。

3.1 分析模型

图5给出了棱柱网格翘曲现象形成机制的分析模型，采用单位长度的方形平板。该平板模型左下角位于坐标原点，有4条边界棱线，每条棱线均匀分布101个网格点，平面网格为了便于显示，在平板中心位置进行了粗化处理，整个平面网格由4 932个三角形单元组成。每条边界棱线沿着平板法向(z轴)推进了20层，第1层高度为0.001，整个推进高度H为0.1。模拟曲率或法矢变化效应的位移扰动添加在y=1.0的边界棱线上。

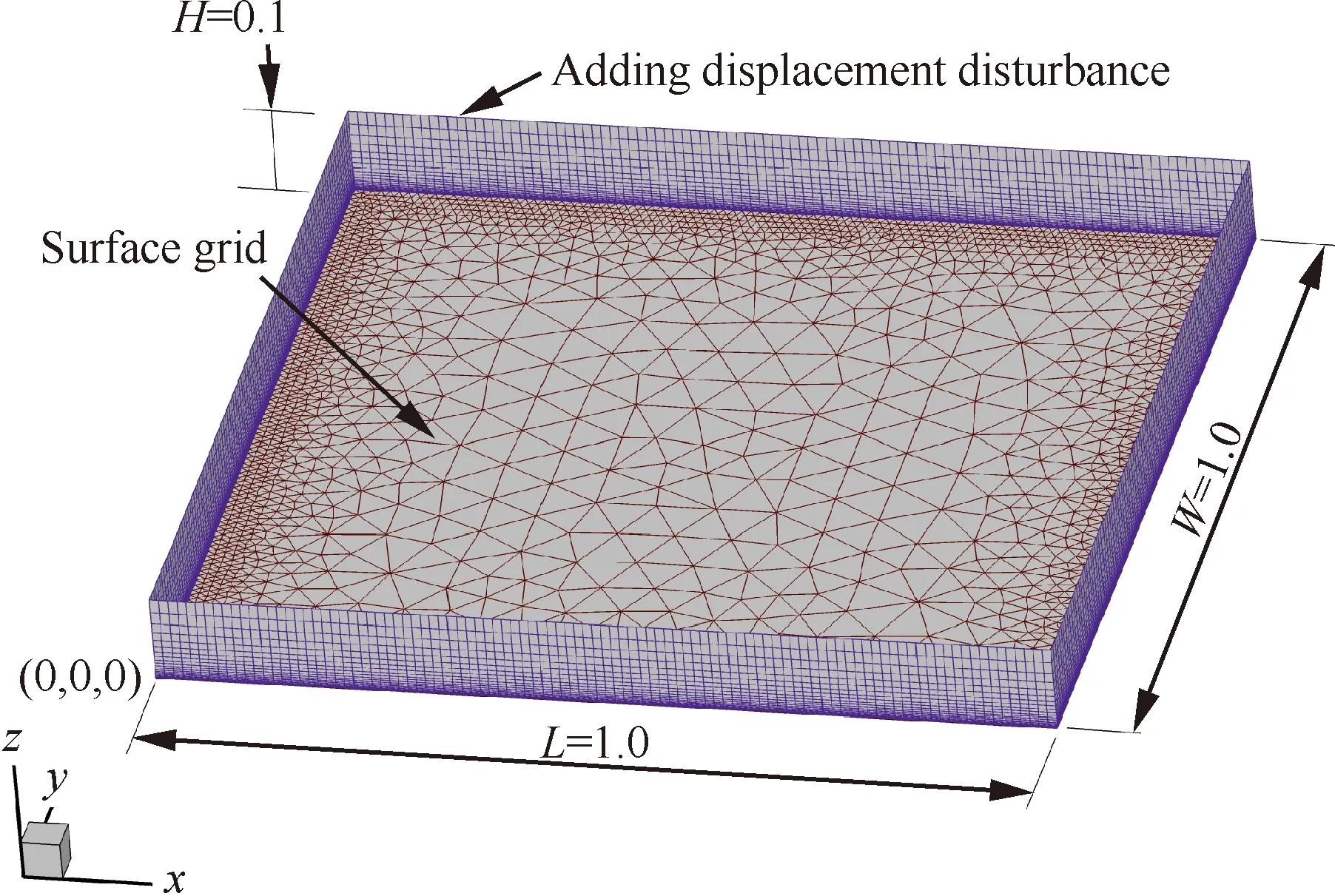
图5 平板棱柱网格生成测试算例

3.2 位移扰动信号

推进位移沿着各个方向的分量随着物面曲率或推进法矢发生变化，推进方向变化越急，推进位移分量改变越快，推进方向变化越慢，推进位移分量改变越慢。因此，不同曲率或法矢改变引起的推进位移分量变化采用不同波长的正弦扰动信号来进行模拟，长波信号用来模拟曲率变化缓慢的情况，短波信号用于模拟曲率变化剧烈的情况。

图6给出了添加的位移扰动信号，这里使用了3种扰动信号，长波信号Signal 1、短波信号Signal 2和混合信号Signal 3。长波信号和短波信号的扰动幅值均为0.01，波长分别为0.5和0.04，混合信号为长波信号与短波信号的线性叠加。

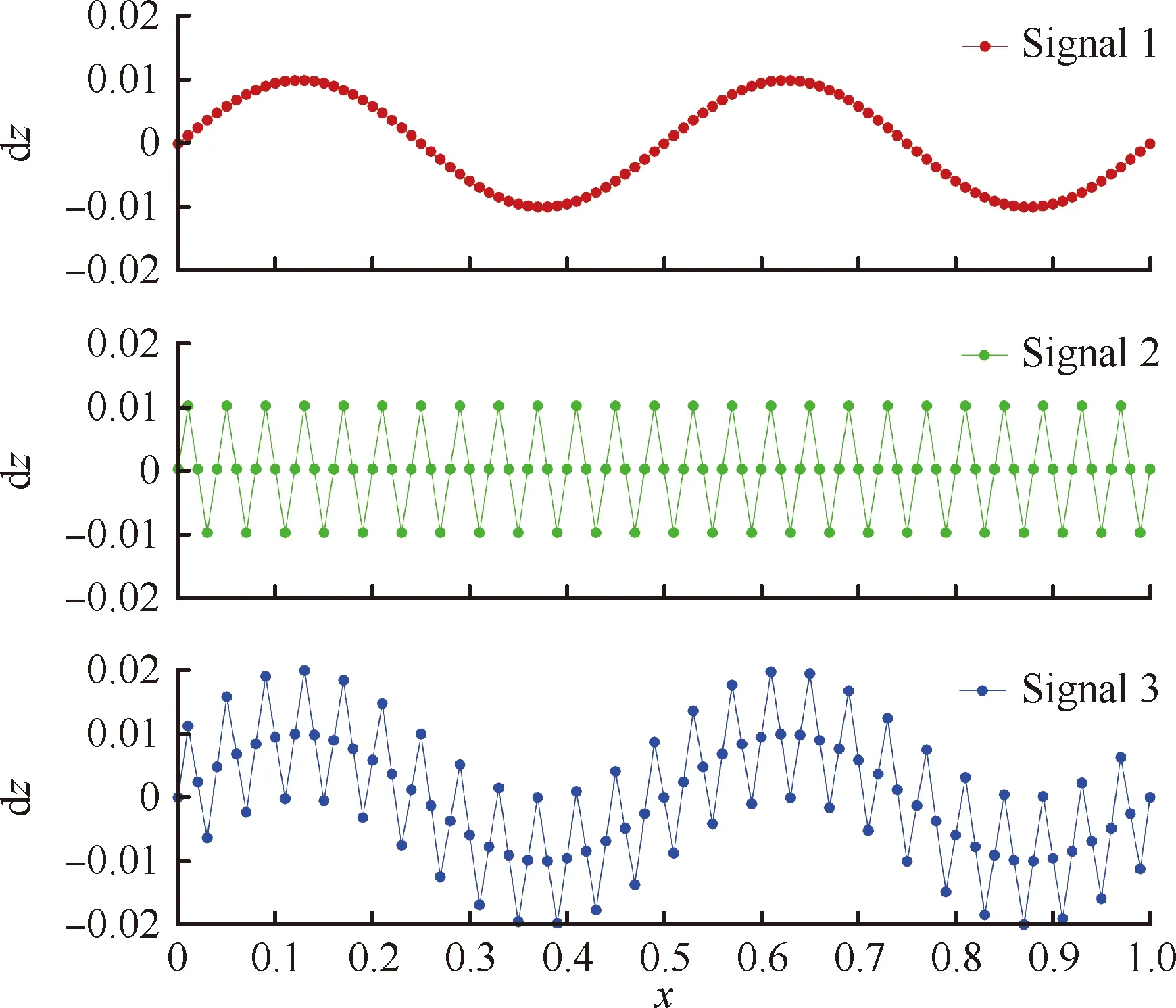
图6 位移扰动信号

位移扰动信号添加到y=1.0位置边界棱线的空间推进面网格的最外层网格点上，空间推进面网格的内部网格点的位移扰动根据推进方向上的网格点分布线性插值得到。

3.3 扰动测试

图7给出了长波扰动信号下的平板棱柱网格生成。可以看出，长波扰动信号添加后，y=1.0位置边界棱线推进位移缓慢地起伏变化，但沿x方向的整体分布依然保持着光滑的特性，如图7(a)所示；扰动位移添加后生成的棱柱网格在靠近y=1.0位置存在微小的起伏变化，但扰动效应迅速衰减，并没有在整体棱柱网格中诱导出明显的翘曲，如图7(b)所示。

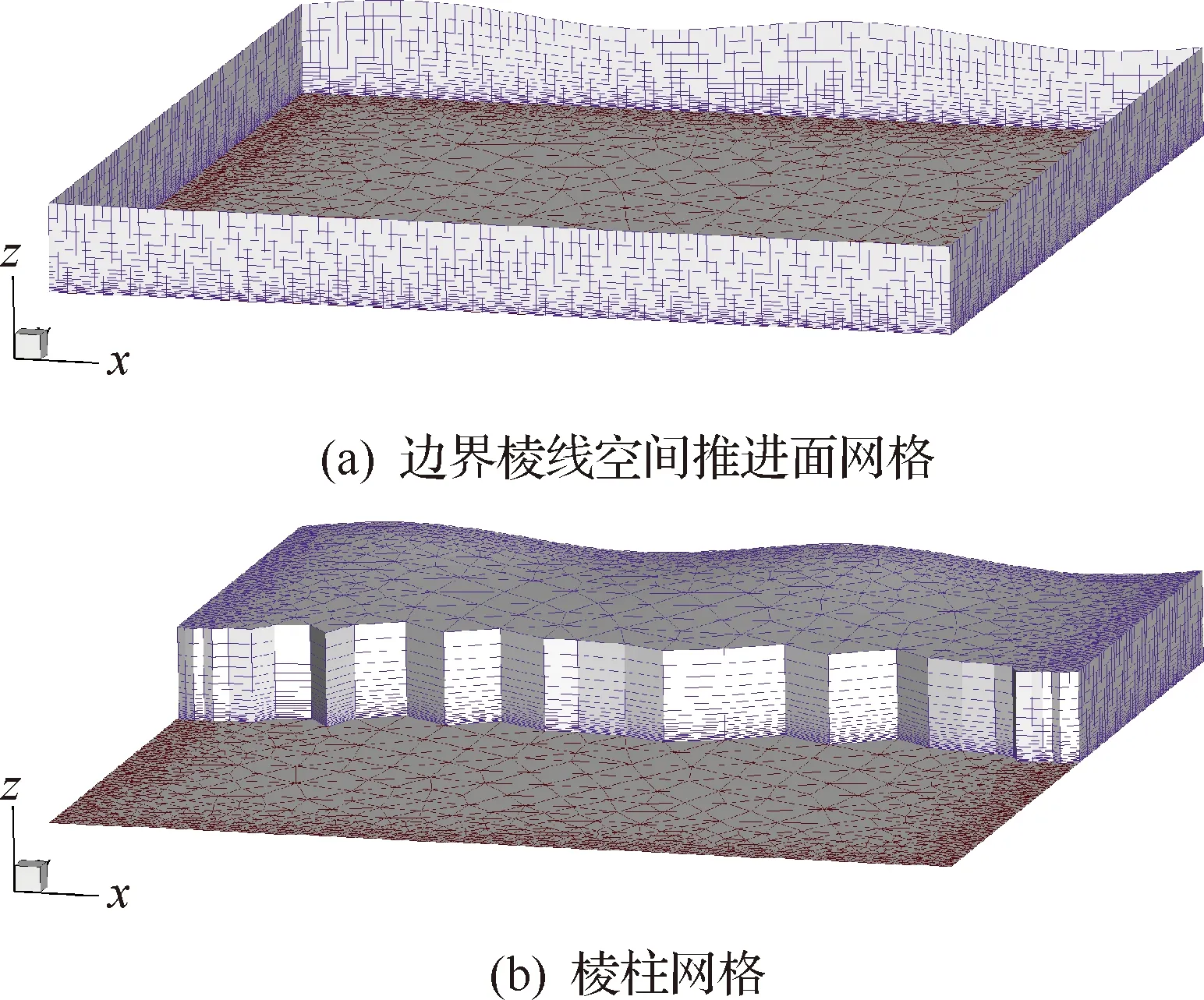
图7 长波扰动信号下的平板棱柱网格生成

图8给出了短波扰动信号下的平板棱柱网格生成。可以看出，短波扰动信号添加后，y=1.0位置边界棱线推进位移快速剧烈地变化，沿x方向的整体分布不再保持光滑，呈现锯齿形的波动，如图8(a)所示；扰动位移添加后生成的棱柱网格在靠近y=1.0位置并没有明显的变化，但扰动效应却在整体棱柱网格中被放大，诱导出显著的翘曲现象，靠近x=0的区域产生了明显的凸起，在靠近x=1.0区域产生了明显的凹陷，如图8(b)所示。

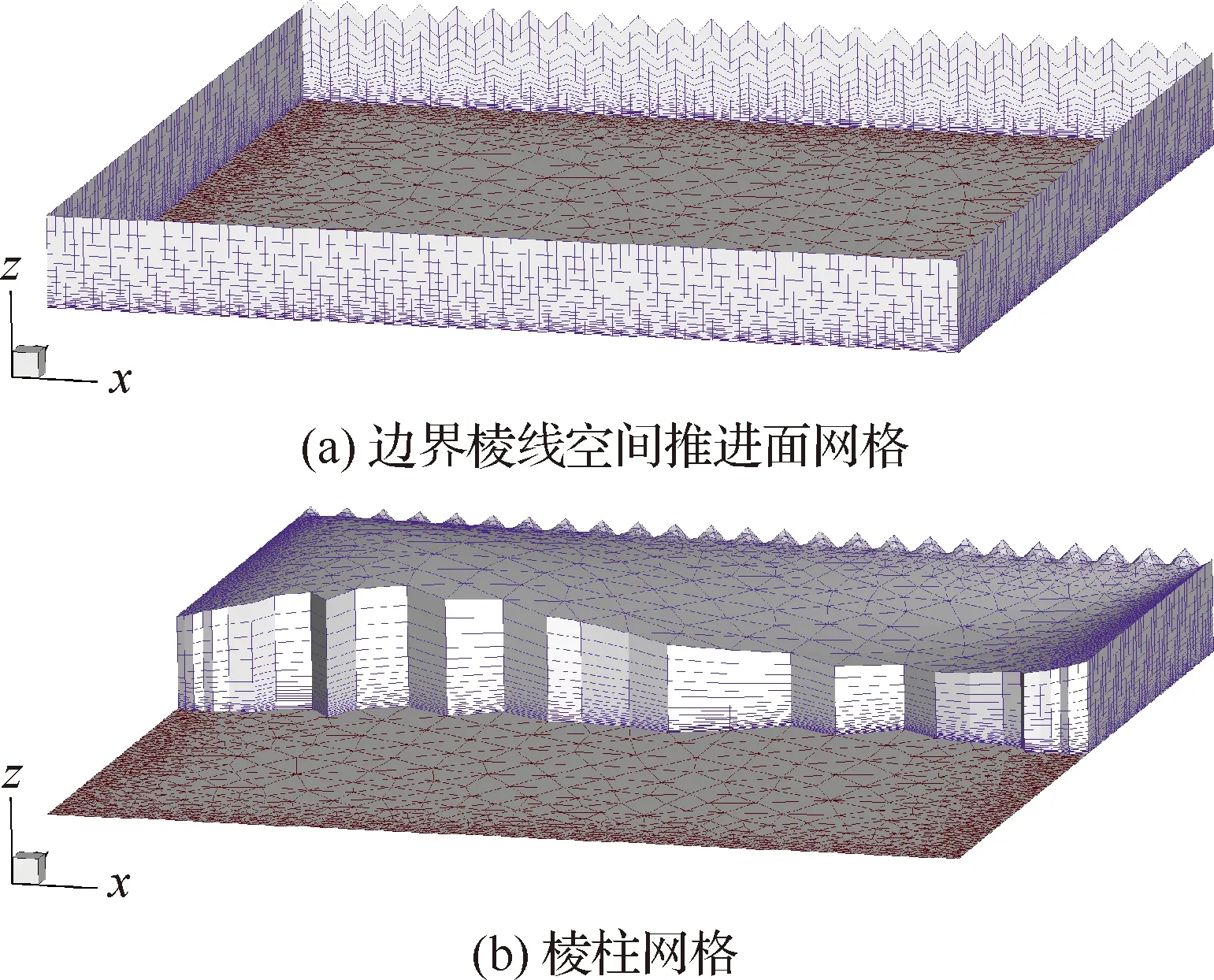
图8 短波扰动信号下的平板棱柱网格生成

图9给出了混合扰动信号下的平板棱柱网格生成。可以看出，混合扰动信号和短波扰动信号的情况相似，y=1.0位置边界棱线推进位移出现快速剧烈的变化，并伴随缓慢的起伏，位移分布光滑性不再存在，呈现锯齿形的波动，如图9(a)所示；扰动位移添加后生成的棱柱网格也出现了相似的翘曲现象，靠近x=0的区域凸起，靠近x=1.0区域凹陷，如图9(b)所示。

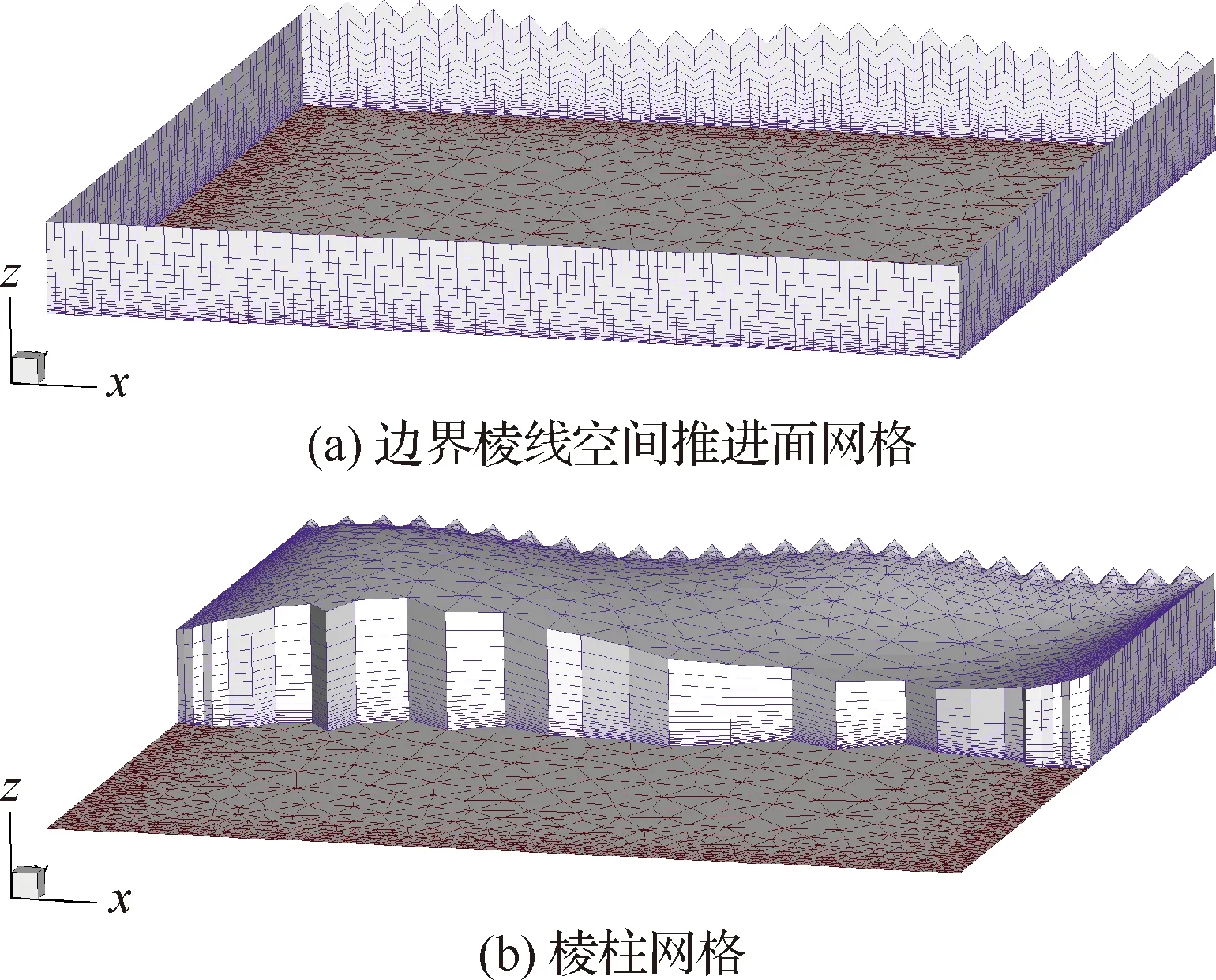
图9 混合扰动信号下的平板棱柱网格生成

3.4 翘曲产生机制分析

从3.3节的平板棱柱网格生成测试中可以得出，边界棱线推进位移分布不光滑将诱导棱柱网格产生明显的翘曲现象。但平板与DLR-F6机翼棱柱网格生成中的翘曲现象有所差异，平板棱柱网格的翘曲不仅有凸起的鼓包，还存在凹陷，而DLR-F6机翼棱柱网格的翘曲体现为鼓包。

进一步测试发现，棱柱网格翘曲的表现形式受边界扰动信号的影响。图10给出了一组不同的短波扰动信号，其中Case I采用3.2节中的短波扰动信号Signal 2，Case II在Case I信号的基础上通过减小波长使得整个边界棱线上增加半个周期的扰动，Case III在Case II信号基础上相位提前180°。

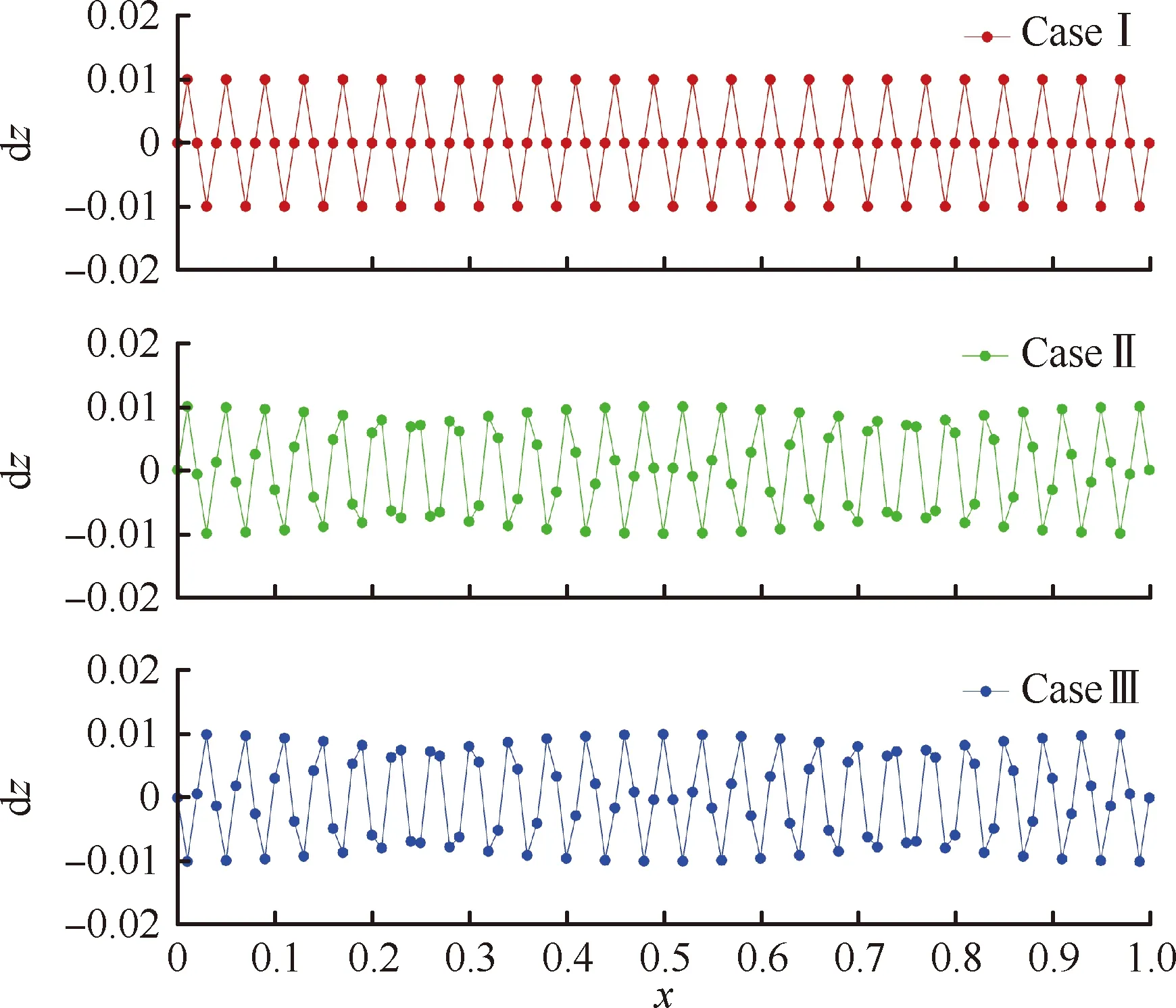
图10 不同的短波扰动信号

图11给出了不同短波扰动信号下的平板棱柱网格生成。可以看出，在Case I扰动信号作用下，平板棱柱网格翘曲表现为凸起和凹陷；在Case II扰动信号作用下，平板棱柱网格翘曲表现为凸起；在Case III扰动信号作用下，平板棱柱网格翘曲表现为凹陷。图11表明棱柱网格的翘曲存在多种表现形式，受边界棱线推进位移分布的影响。DLR-F6机翼棱柱网格的翘曲与Case II短波扰动信号作用下的平板棱柱网格的翘曲相似，是多种翘曲表现形式中的一种。

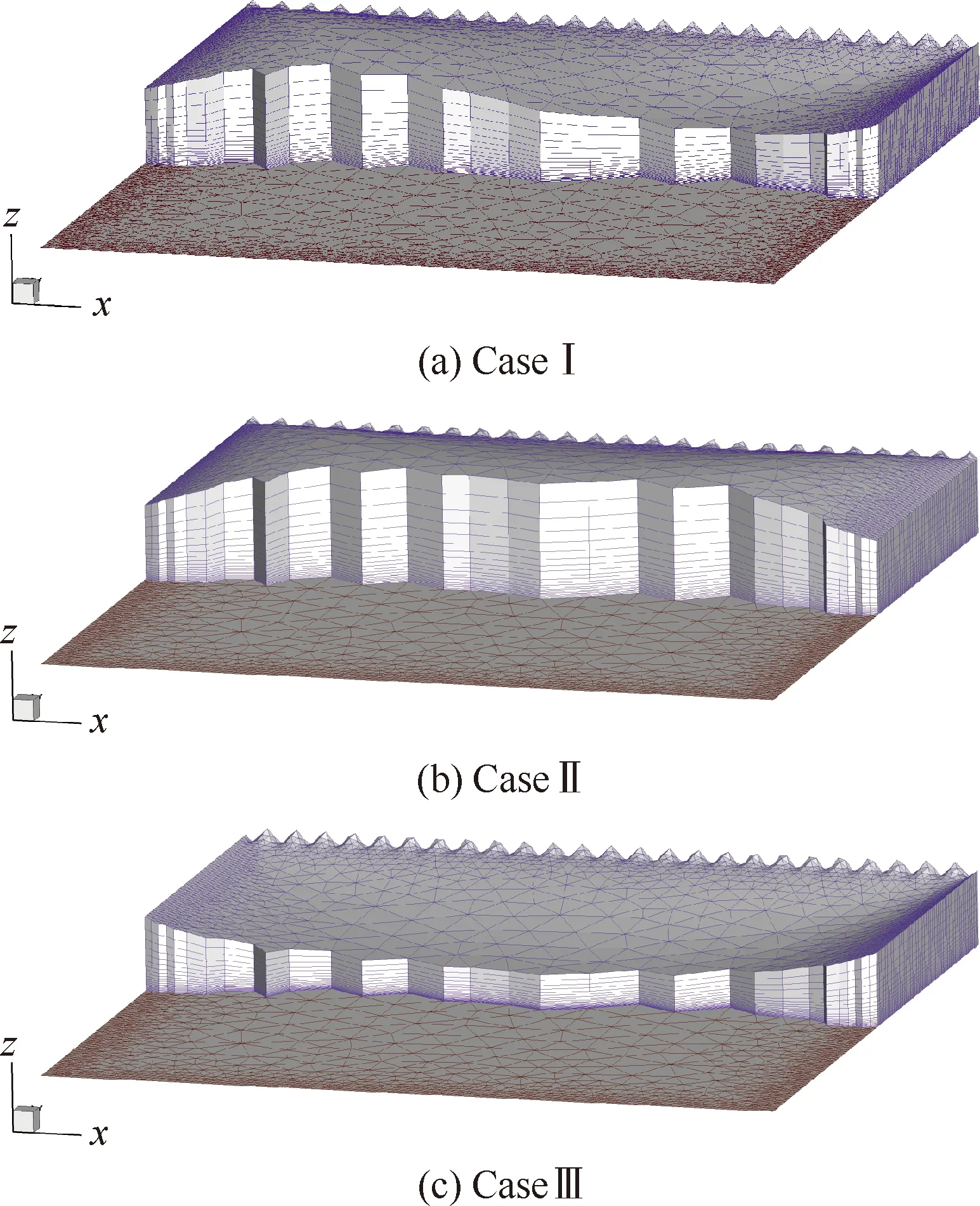
图11 不同短波扰动信号下的平板棱柱网格生成

上述结果间接验证了本节开始的猜测，从而阐释清楚交互式棱柱网格生成中翘曲现象的形成机制：曲率或推进法矢的剧烈变化引起推进位移的快速改变，造成边界棱线推进位移分布的不光滑，诱导棱柱网格生成出现翘曲现象。

4 翘曲消除算法

图12给出了不同扰动信号下平板棱柱网格y=0.5位置的剖面形状，图中扰动信号仍然使用3.2节中图6所示的3种信号。可以看出，叠加了Signal 1和Signal 2的Signal 3诱导产生的棱柱网格翘曲与Signal 2的结果十分接近，说明棱柱网格翘曲主要由短波信号分量引起，长波信号分量的贡献十分小。

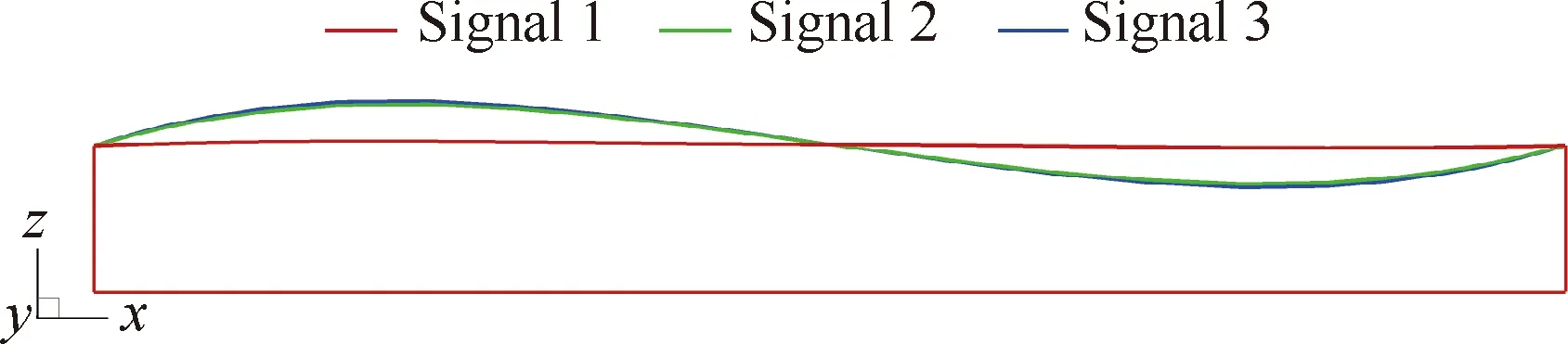
图12 平板棱柱网格剖面形状(y=0.5)

不同波长信号的贡献差异性为解决棱柱网格生成中的翘曲问题提供了一种可行的思路：通过对推进位移分布中的短波分量进行过滤，使推进位移分布光滑，从而消除网格翘曲。

拉普拉斯光顺方法对不同波长信号的耗散特性存在明显的差异，波长越短，信号衰减越快，波长越长，信号衰减越慢[28]。因此，本文采用基于拉普拉斯的思路发展面向边界棱线空间推进位移分布的光顺算法。

图13给出了Laplace光顺算法用于平面曲线的示意图，图中Pi为平面曲线上的第i个点，li-1, i表示点Pi-1与点Pi之间的距离，li, i+1表示点Pi与点Pi+1之间的距离。

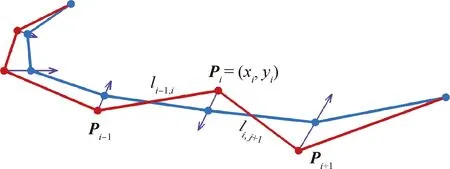
图13 Laplace光顺算法示意图

Laplace算法的迭代过程可以表示为

(1)

式中：n表示当前迭代步；n+1表示下一时刻迭代步；λ为松弛因子，取值范围为0～1；L(·)为Laplace算子，可以表示为

(2)

式(2)中的Laplace算子假定曲线上点均匀分布的情况，对于非均匀分布的点，可以表示为

(3)

本文中待光顺的Pi分别为(s, dx)、(s, dy)、(s, dz)，其中s为边界棱线网格点相对起始点的曲线距离，通过分布线段线性叠加得到，dx、dy、dz分别为边界棱线推进位移在3个坐标方向的分量。

5 结果与讨论

图14给出了边界棱线推进位移拉普拉斯光顺后生成的DLR-F6机翼棱柱网格，每个网格块边界棱线的光顺次数统一设为20，松弛因子λ选择0.5。可以看出，前后缘附近区域的翘曲现象被消除，棱柱网格外推进面保持光滑规则的形状，如图14(a)所示；仍然选取z=217，245 mm两个剖面，并和光顺前的剖面形状比较，可以发现，机翼前后缘附近位置棱柱网格的鼓包现象被抑制，光顺后的棱柱剖面形状更加光滑，且光顺过程对未发生鼓包现象的中部区域的作用很小，如图14(b)和图14(c)所示。图14的结果表明发展的基于拉普拉斯的光顺算法能够消除棱柱网格生成中的翘曲现象。

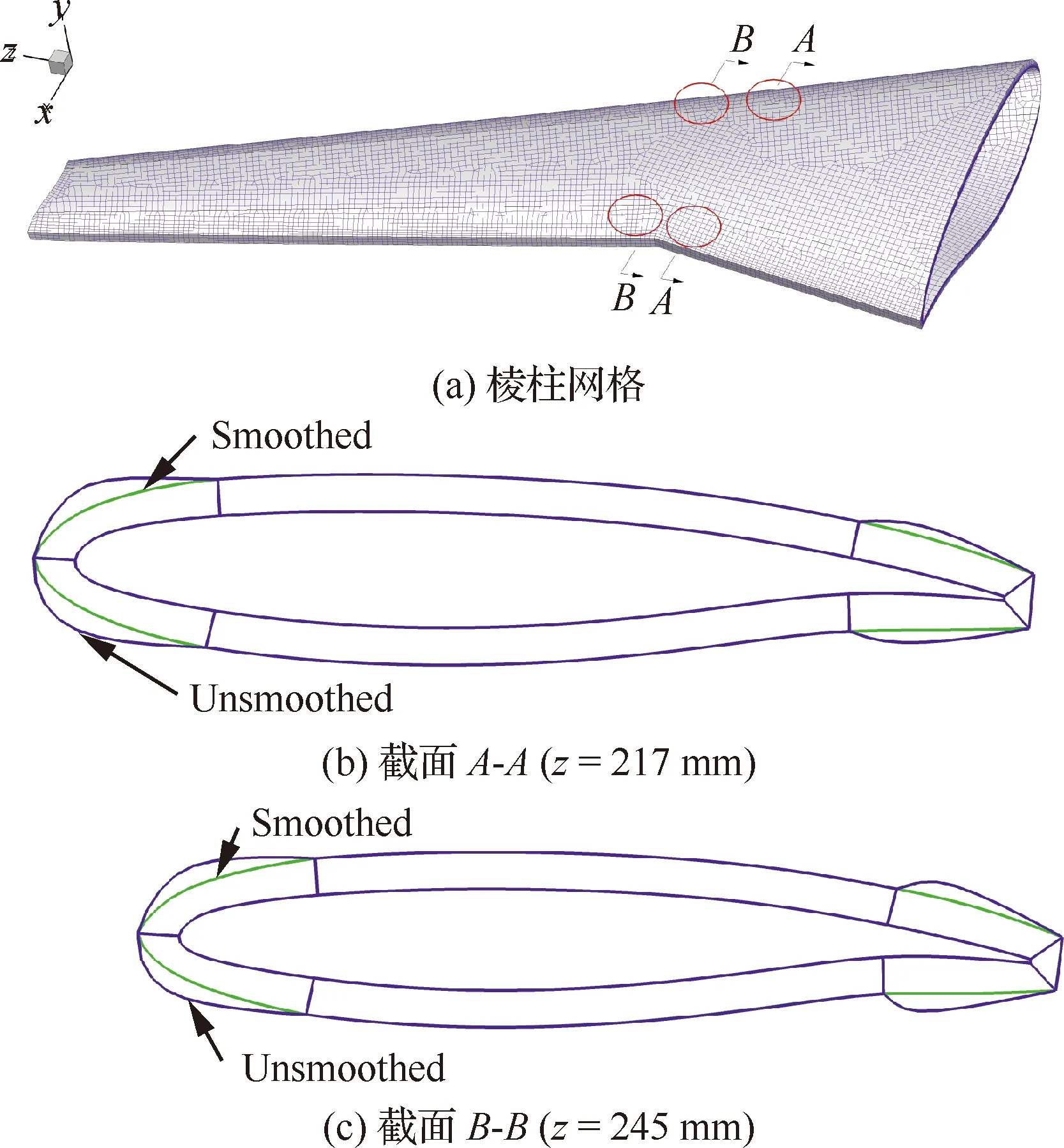
图14 DLR-F6机翼棱柱网格生成(光顺后)

图15给出了不同光顺次数下DLR-F6机翼棱柱网格z=217 mm位置的剖面形状。可以看出，随着光顺次数的增加，光顺后的外轮廓线更加趋向直线。对于后缘位置，曲率变化平缓，光顺次数越多，外轮廓线愈光滑，但对于前缘位置，曲率变化明显，光顺次数太大，会引起部分前缘区域的棱柱网格被压缩，导致网格正交性降低。针对本文DLR-F6机翼算例，前缘位置的光顺次数在5附近，后缘位置的光顺次数大于20，能够获得较好的棱柱网格生成。图15结果表明，针对不同区域，棱柱网格生成中的光顺次数具有不同的最优值。

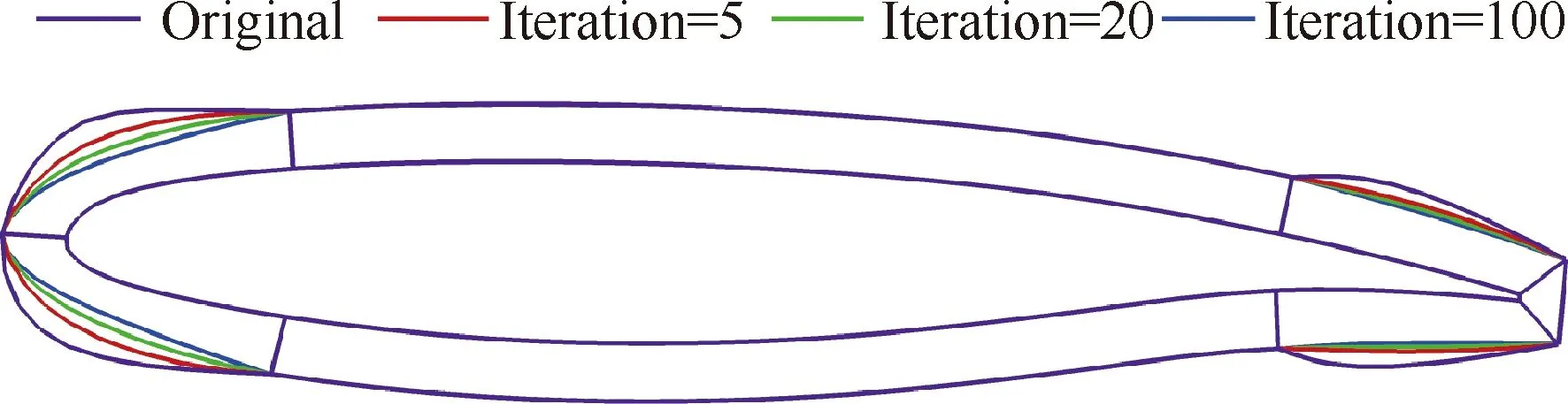
图15 不同光顺次数下DLR-F6机翼棱柱网格剖面形状(z=217 mm)

图16给出了DLR-F6翼身组合体构型的棱柱网格生成，该构型表面网格有18 371个网格点，16 077个四边形单元，642个三角形单元。棱柱网格生成的参数，如第1层网格高度、网格增长速率、推进层数，均与前文DLR-F6机翼的相同，光顺次数仍然统一选择为20。可以看出，整个棱柱网格的外推进面保持规则的形状，棱柱网格单元的连续性和正交性很好，整体网格具有较高的质量。图16的算例表明，完善后的棱柱网格生成方法具有在工程复杂外形中广泛应用的潜力。