几何尺寸约束的超燃冲压发动机推力喷管设计

陈以勒，俞凯凯，徐惊雷

南京航空航天大学 能源与动力学院，南京 210016

超燃冲压发动机是高超声速飞行器的主要动力选择，具有结构简单、无需自身携带氧化剂、有效载荷大等优点，作为高超声速技术实现的关键，是近年来国际研究的热点之一[1-4]。超燃冲压发动机一般主要由4部分构成，分别为进气道、隔离段、燃烧室和尾喷管[5-6]。其中尾喷管是提供推力的重要部件，特别是当马赫数超过6时，喷管可以产生约占整个推进系统70%的净推力[7]。这说明喷管的性能将直接影响超燃冲压发动机乃至高超声速飞行器的性能，因此研究者们尝试各种手段以提高喷管的气动性能[8-11]。此外，由于超高声速飞行器通常要求机体/推进系统一体化，进而对喷管的几何尺寸产生了一定限制，因此喷管设计方法除了需要考虑其气动性能的优化，还需要兼顾几何约束的要求。

为提升喷管的气动性能，Rao[12]采用变分法推导了最大推力理论，在此基础上提出了一种最大推力的火箭喷管设计方法。最大推力理论在后来的喷管设计中得到广泛的应用。Mo等[13]基于最大推力理论提出了一种非对称喷管的设计方法，并应用该方法考虑非均匀来流设计喷管，最终可使喷管推力系数、升力和俯仰力矩分别提高1.75 %、 6.51 %和 6.25 %。Lv等[14]提出了一种基于特征线法的喷管设计方法，讨论了下壁面长度对喷管性能的影响，该方法可以使喷管轴向推力系数、升力以及俯仰力矩分别增加5.5%、1 098.2% 和20.3%。Lu等[15]将Rao理论与流线追踪技术相结合，设计了三维超燃冲压发动机喷管，结果表明该方法可使喷管的推力和升力分别提升2.7%和69.5%。

为满足喷管的几何约束，Argrow和Emanuel[16]发展了最短喷管理论并用于喷管设计，但采用该方法设计得到的理想膨胀喷管仍然较长，难以满足推力喷管的几何约束。Shyne和Keith[17]提出可以利用截短方法使喷管满足尺寸约束并达到减重的目的，结果表明需要在喷管的重量和性能损失上做出权衡。Hoffman[18]提出了一种压缩型截短喷管的设计方法，应用该设计方法可有效缩短喷管长度，且压缩型截短喷管的性能与 Rao 喷管性能相差仅0.04%～0.34%。

在现有的喷管设计方法中，尽管有些方法可以满足部分尺寸约束[16-18]，但却未能充分利用几何空间来提升喷管气动性能。因此，本文提出一种几何尺寸约束的超燃冲压发动机推力喷管设计方法，实现对喷管长度和高度的约束，同时优化其气动性能。并且通过2个设计因子实现对喷管设计的主动控制，以满足实际应用过程中针对喷管的不同性能需求。本文首先详细介绍了提出的喷管设计原理与过程；其次校核了所使用的数值模拟方法的有效性，并确定了网格分辨率；然后，采用数值模拟对本文提出的设计方法进行了有效性验证；在此基础上，开展了2个设计因子对喷管性能影响的研究；最后，通过与典型截短设计方法进行对比分析，验证了本文提出的设计方法的优越性。

1 喷管设计方法

1.1 特征线法

特征线法(Method of Characteristic, MOC)是一种用于求解双曲型偏微分方程的通用数学方法，其在超声速领域得到了广泛的应用[12-15]。定常二维、平面或轴对称的等熵超声速流动的控制方程如式(1)所示。通过有旋特征线法可以对目标流场构造特征线网格，如图1所示。其中任意节点均会发出3条特征线，分别为左行特征线C+，右行特征线C-和流线C0，分别对应特征方程式(2)和式(3)。

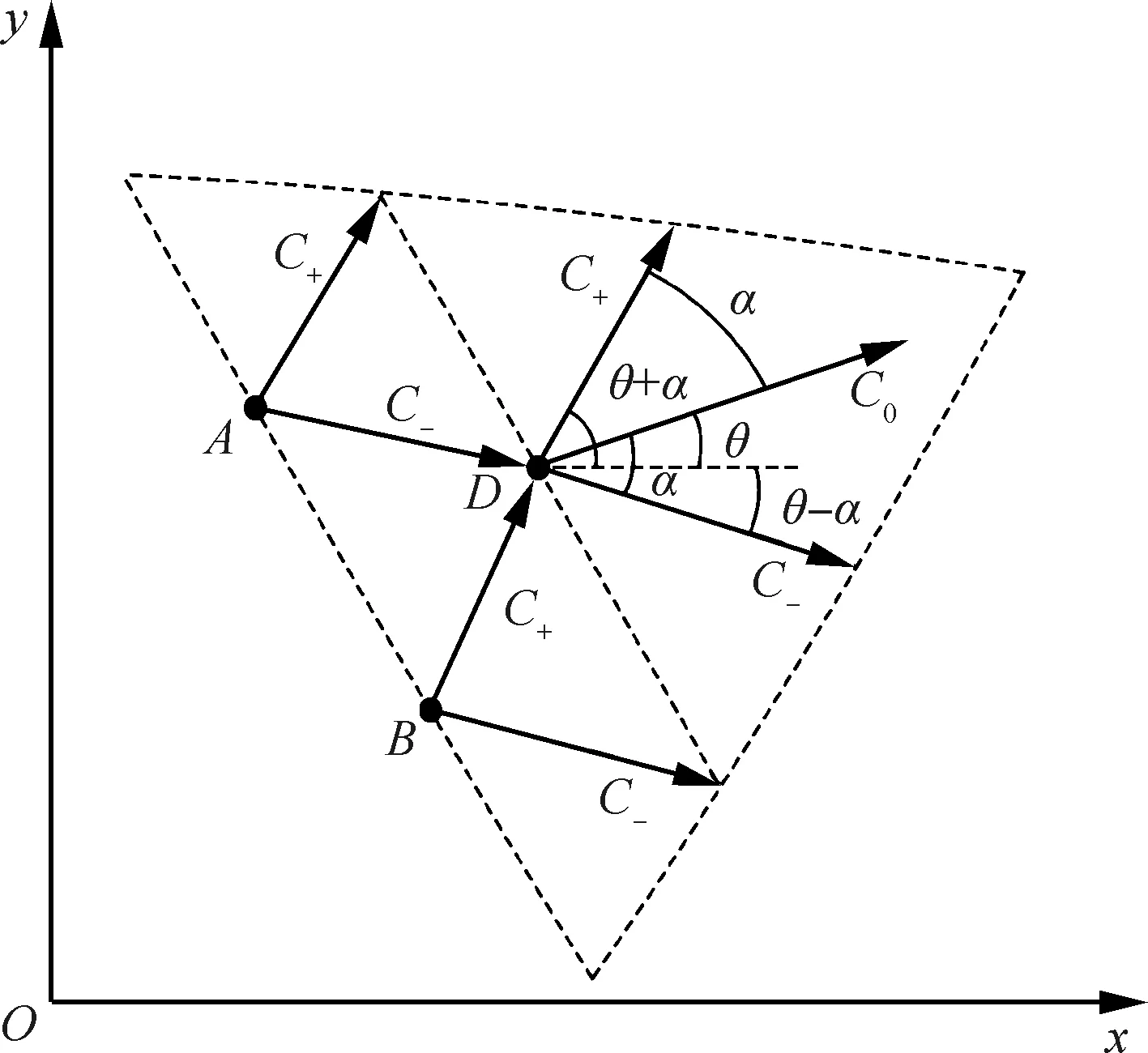
图1 特征线网格

(1)

(2)

(3)

式中：θ为流动角；α为马赫角；ρ为密度；p为静压；a为声速；u为x方向的速度分量；v为y方向的速度分量；ux为u在x方向的导数，其余类似表达含义类似；δ表示流动类型(对于平面流取0，轴对称流取1)。特征方程对应的相容性方程为

ρVdV+dp=0

(4)

dp-a2dρ=0

(5)

(6)

其中：Ma为马赫数；V为速度。通过数值程序求解式(2)～式(6)，就可以获得目标流场内各节点的气动参数。此外，根据节点的类型可以分为几种不同的单元过程，本文提出的设计方法主要包括3种类型的节点：内点、壁面点和变向区域点，单元点的具体求解方法可以参考文献[19]。

1.2 最大推力理论

为提升喷管气动性能，本文提出的设计方法采用了最大推力理论。Rao提出的最大推力理论目前已得到广泛应用[13-15]，研究结果表明最大推力理论具有显著的优越性。在此基础上发展出了二维最大推力理论，二维情况时最后左行特征线上的气动参数需满足式(7)和式(8)，具体的理论推导过程可见文献[14]。

(7)

ρV2sin2θtanα=C2

(8)

式中：C1、C2均为常数。图2为几何尺寸约束的推力喷管设计方法示意图。喷管内各区域的设计细节如图3所示。因此，为实现喷管推力最大化，沿最后左行特征线KuM上的气动参数均需满足式(7)和式(8)，其中C1、C2的值可由上位关键点Ku的气动参数计算得到。同理，沿最后右行特征线KdN上的气动参数可采用相似的方法确定[20]。值得注意的是，本文提出的设计方法根据几何约束确定最大推力理论中的压力条件。

图2 喷管设计过程示意图

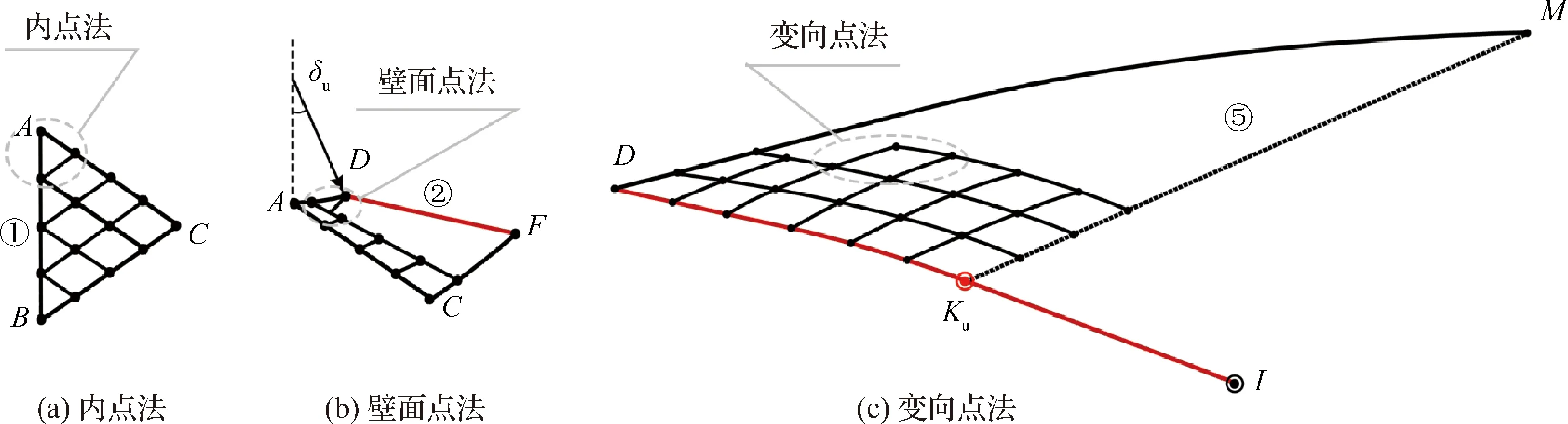
图3 各区域设计过程

1.3 喷管设计步骤

为克服以往方法未能充分利用几何空间提升喷管气动性能的问题，本文提出了一种直接从几何约束(包括长度约束和高度约束)出发的设计方法，该设计方法结合了最大推力理论，可以使喷管在满足几何约束的同时优化其气动性能。一般来说，进口条件和高度约束可以基本确定喷管内气流膨胀程度。但是为了进一步有效控制喷管几何尺寸并提升气动性能，本设计方法引入2个设计因子，即比例因子和非对称因子，用于实现对喷管设计的主动控制，以满足实际应用过程中的不同性能参数需求。其中，比例因子用于确定核心点的设计参数，从而实现喷管内气流膨胀程度可控，进一步提升喷管气动性能。非对称因子则用于控制喷管上、下壁面的非对称膨胀程度，以平衡推升力。图4为本文提出的设计方法的流程图。具体设计过程如下。

图4 喷管设计流程

步骤1根据喷管的进口参数和高度约束，利用一维流理论确定完全膨胀下喷管的出口马赫数，并将其作为喷管设计过程中的初始马赫数Ma0：

q(Ma0)Ae=q(Main)Ain

(9)

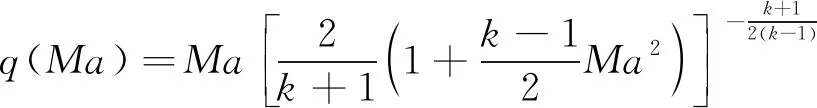
(10)

式中：Ma0为初始马赫数；Main为喷管进口马赫数；Ae为喷管出口截面面积；Ain为喷管进口截面面积；k为气体比热比。

步骤2确定比例因子β，利用式(11)和等熵关系式，获得喷管的设计马赫数Mad以及其他气动参数。

Mad=β·Ma0

(11)

步骤3确定上壁面初始膨胀角δu，并利用式(12)得到下壁面初始膨胀角δd。根据喷管进口参数分布，初始膨胀段以及下壁面直线EE′，利用特征线法便可以求解区域①、②、③和④，并得到上下膨胀段发出的最后特征线的交点，即核心点I。其中，区域①的求解过程见图3(a)。由特征线法可知，对于一条非特征线的初值线，可以采用单元过程中的内点法求解其影响域。在本设计方法中，进口条件确定了初值线AB，因此利用内点法对区域①进行求解，并获得线AC上的流动参数。然后，根据式(13)和δu确定上初始膨胀段AD，并进一步采用壁面点法即可获得线AD上各节点的流动参数。在此基础上，利用内点法求解区域②，如图3(b)所示。区域③和④的求解同理。需要注意的是，线EE′为一条可变直线，其长度在核心点I的迭代过程中确定。

(12)

y=b1x2+b2

(13)

式中：φ为非对称因子，表征上、下壁面膨胀程度的非对称性；x和y分别为节点的横、纵坐标；b1和b2为常数。

步骤4为了使核心点I的气动参数满足步骤2中的设计要求，需要对步骤3进行迭代，得到满足式(14)的上初始膨胀角δu和下壁面直线EE′的长度ld。进一步获得区域①、②、③、④的流动参数。

(14)

步骤5在上膨胀段AD发出的最后特征线DI上构建上位关键点Ku的求解空间。区域⑤的求解过程如图3(c)所示。利用最大推力理论确定沿着上位关键点Ku发出的左行特征线KuM上的流动参数，进一步借助变向点法求解区域⑤。此外根据流量守恒原理，流经特征线KuM的流量与通过特征线DKu的流量相等，并以此逐个确定构成型线DM的各点参数，获得壁面型线AM。

需要注意的是，此时的壁面AM未必满足长度约束，因此在求解空间DI中，采用二分法寻找到合适的Ku点以保证喷管的长度在约束范围内，并求解出待设计的推力喷管上壁面AM。

步骤6类似步骤5，采用相同方法，根据高度约束确定下位关键点Kd并获得待设计的推力喷管下壁面BN，完成喷管设计。

2 数值模拟方法

2.1 数值方法有效性

本文采用计算流体力学方法(Computational Fluid Dynamics, CFD)来获得喷管的流场结构和气动性能，数值方法中的控制方程为二维、稳态、可压缩的雷诺平均Navier-stokes方程，利用有限体积法对控制方程进行离散，控制面上的无黏通量采用Roe-FDS通量差分格式获取，湍流模型使用Shear Stress Transport(SST)k-ω两方程模型。为了准确获取壁面处的流动信息，对壁面附近网格进行加密，壁面处y+约为1。在数值模拟过程中，采用了压力入口、压力出口和压力远场等边界条件。

为验证上述数值方法的有效性，对文献[13]中的喷管利用上述方法进行数值模拟校核。该喷管的几何构型和计算网格如图5所示，其中模型的几何尺寸使用喷管的喉部高度ht进行无量纲化。根据文献[13]中的实验工况确定数值模拟中进出口边界条件。数值模拟得到的喷管壁面压力与实验结果(EXP)对比如图6所示，并利用进口总压p*对压力分布进行无量纲化。从图中可以看到该数值方法能够准确地获得喷管内的压力变化，壁面压力的平均相对偏差仅为4.9%，因此可以证明上述数值方法的有效性和准确性。

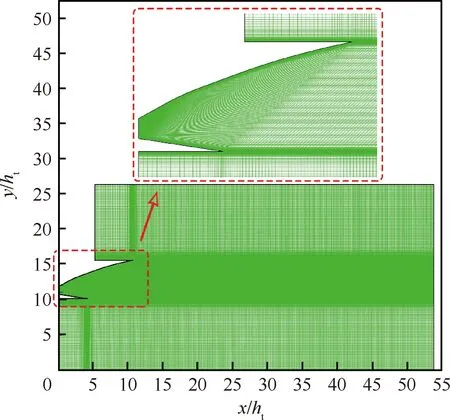
图5 喷管计算网格

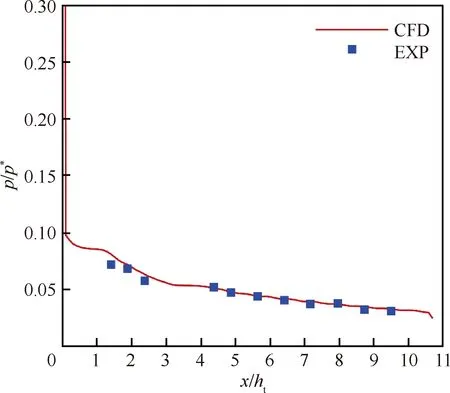
图6 喷管上壁面压力分布

2.2 网格无关性

为消除计算网格分辨率对数值模拟准确性的影响，本节开展了网格无关性研究。喷管构型和远场设置分别如图7中的红色区域和绿色区域所示。对该几何模型使用商用软件ICEM进行网格划分，获得了网格尺寸为粗(Coarse)、中(Middle)、细(Fine)尺度的计算网格(网格量分别为7万、15万和30万)，其中，中尺度网格见图7。相同工况下，不同尺度网格得到的上壁面压力分布如图8所示，可以看到整体上3种尺度网格的压力分布基本一致。但通过局部放大，发现相比中尺度和细尺度的网格，粗尺度网格在x≈0.3, 0.75 m 处压力分布出现较大偏差，最大偏差可达1.72%。因此，说明中尺度网格可以满足计算精度的要求，在下文中均采用中等尺度的计算网格开展研究。

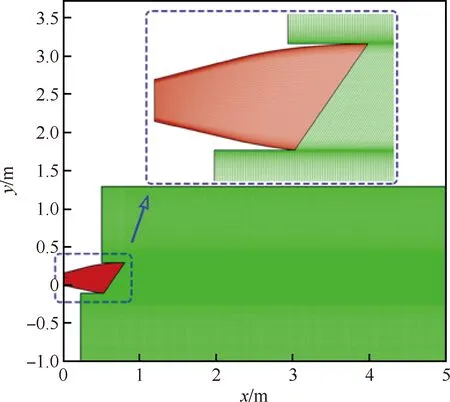
图7 目标喷管的计算域及网格划分

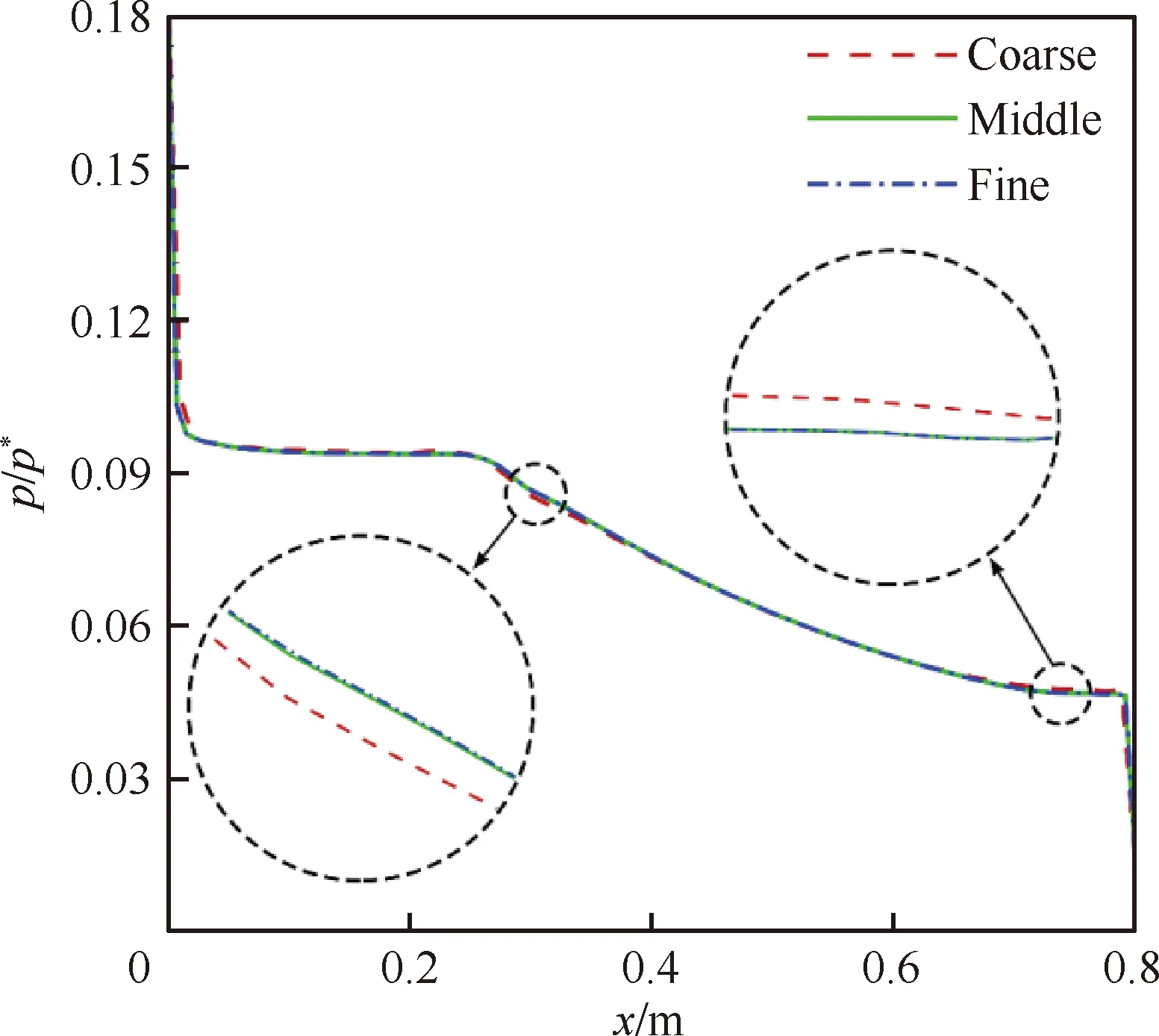
图8 不同尺度网格的喷管上壁面压力分布

3 设计方法研究

3.1 设计实例验证

为验证本文提出的几何尺寸约束的超燃冲压发动机推力喷管设计方法的有效性，本节运用该方法在某典型工况下对喷管进行设计，并对设计得到的喷管进行无黏模拟验证。设计工况和几何约束如表1所示，其中Lc为长度约束，Hc为高度约束，pin为进口压力，Tin为进口温度，Main为进口马赫数，H为飞行高度，Mac为巡航马赫数。此外本验证算例中β取1.02，φ取0.9。设计得到的喷管构型见图9，可以看到喷管的几何尺寸能够满足约束条件。图9为分别通过MOC和CFD获得的喷管在设计工况下运行时的压力云图，可以看到MOC的压力分布与CFD结果基本一致，同时MOC很好地捕捉到了喷管出口附近下壁面的反射膨胀波。此外，MOC获得的壁面压力相对CFD壁面压力结果的平均误差仅为1.36%。由此说明该方法能够有效地设计喷管内流场结构，并获得满足几何约束的喷管型线。

表1 设计工况

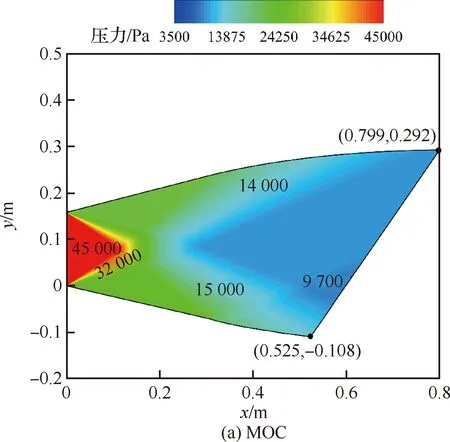
图9 通过MOC和CFD获得的喷管压力云图

3.2 比例因子影响

为研究在设计过程中比例因子对喷管型线以及气动性能的影响，本节使用3个不同的比例因子在相同工况和几何约束下对喷管进行设计，并获得喷管的流场结构和气动性能。设计得到的喷管及其流场结构如图10所示，可以看到比例因子会显著影响喷管构型，进而改变喷管内流场结构。随着比例因子增加，喷管的扩张程度逐渐增加，导致上壁面高度增加，同时由于高度约束的存在，使下壁面逐渐缩短。此外，喷管出口马赫数也随着比例因子的增加而增加。

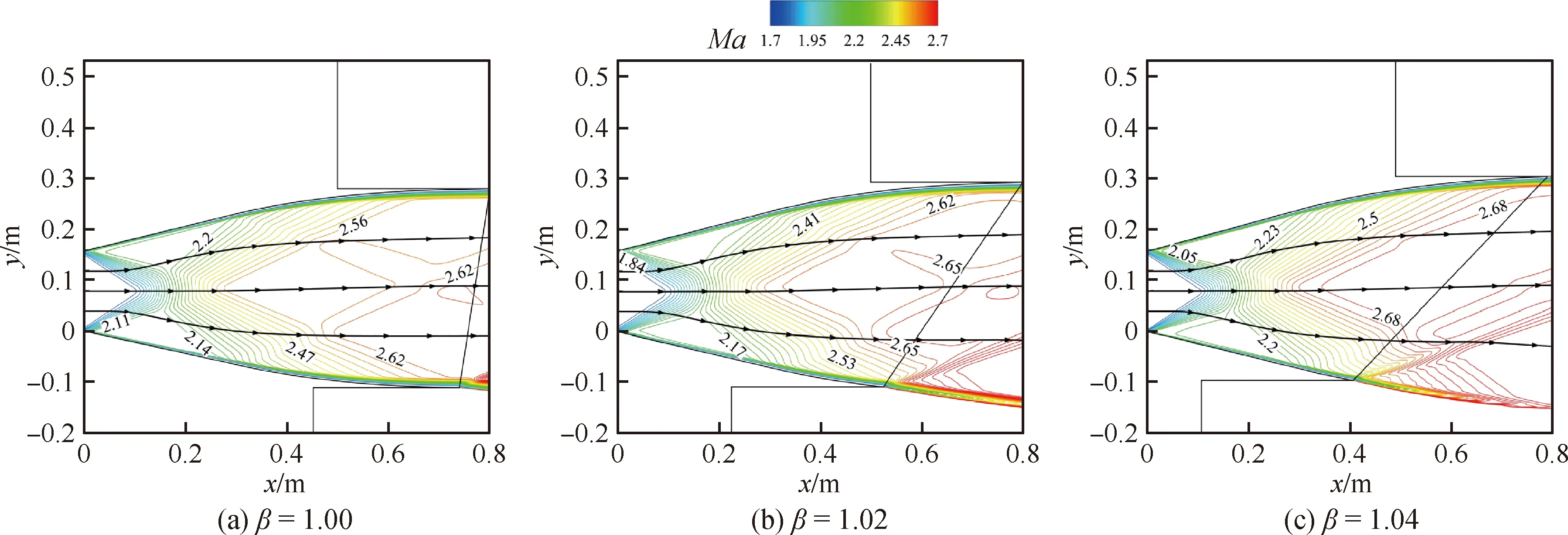
图10 不同比例因子的喷管马赫数云图

表2给出了由不同比例因子设计得到的喷管的气动性能，表中Fx为喷管轴向推力，L为升力，M为俯仰力矩，俯仰力矩的参考中心取在喷管进口下壁面处，Cfx为喷管推力系数，具体计算式为

(5)地表氧化铁帽标志：矿体经风化后，呈黄褐色，具蜂窝状构造，可见有大量的褐铁矿斑点(铁帽)，是找矿的直接标志。

(15)

(16)

(17)

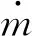
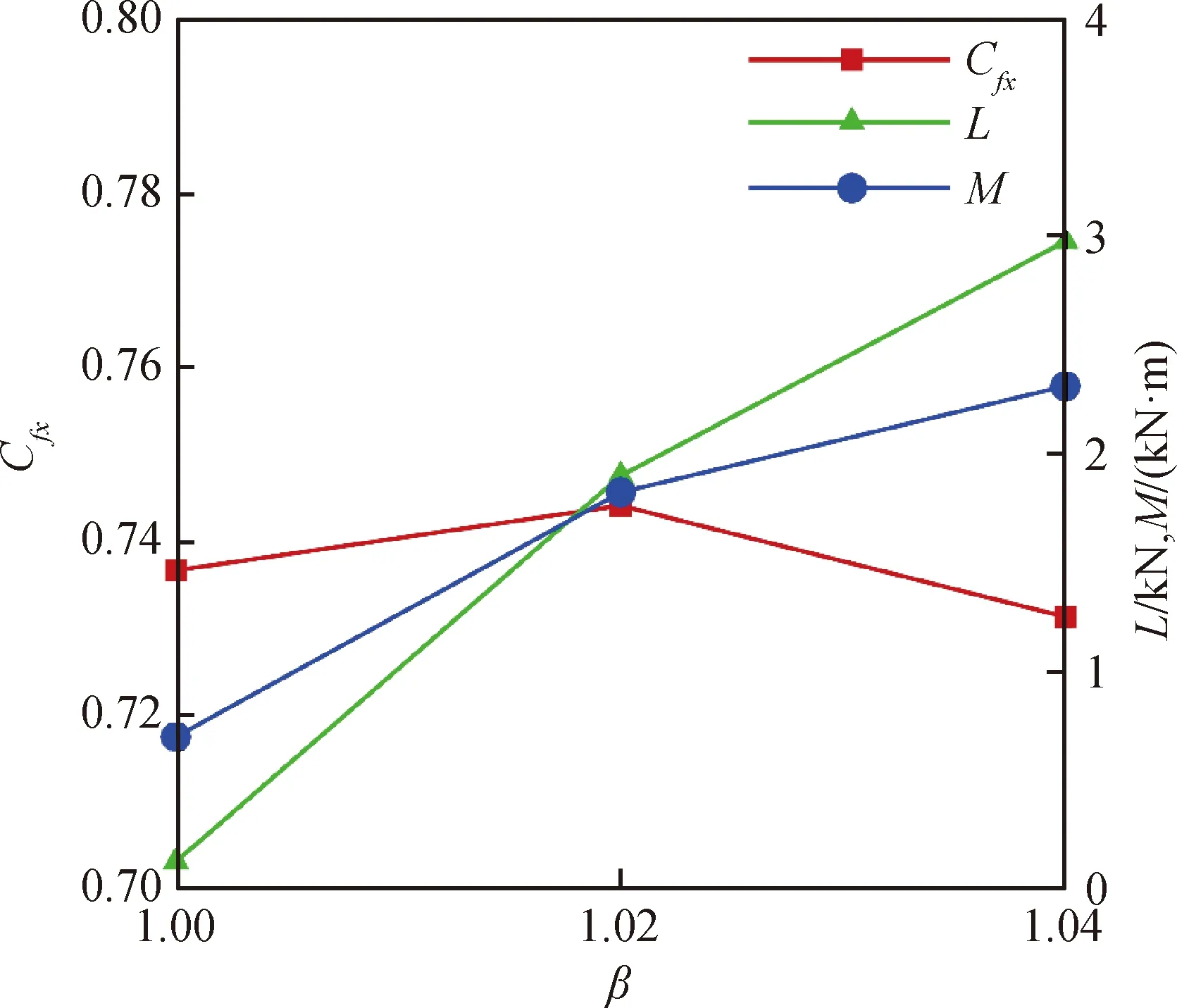
图11 不同比例因子的喷管气动性能分布

3.3 非对称因子影响

为研究非对称因子对喷管设计及性能的影响，本节使用了3个不同的非对称因子分别设计喷管，比例因子均取本研究中推力最优的比例因子，即β=1.02。通过数值模拟可以得到相应的喷管性能和流场结构。由图12可以发现喷管下壁面会随着非对称因子的增加而缩短，下壁面的缩短意味着推力和负升力的有效作用面积减小，这将导致推力降低同时升力增加；此外，喷管上壁面扩张程度出现轻微减小，导致气流膨胀程度降低，从而使上壁面压力增加，这有利于推、升力的增加。

图12 不同非对称因子的喷管马赫数云图

不同非对称因子的喷管气动性能见表3。喷管气动性能随非对称因子的变化趋势如图13 所示。可以看到随着非对称因子逐渐增加，喷管的推力系数逐渐降低，在φ为1.0处达到最小值0.741， 同时喷管的升力和俯仰力矩随着非对称因子的增加而增大，在φ为1.0处达到最大值，分别为3 009.97 N和2 154.46 N·m，这与上述分析结果一致。

表3 不同非对称因子的喷管气动性能

图13 不同非对称因子的喷管气动性能分布

以上研究表明，通过调整比例因子和非对称因子能够实现对喷管气动性能的主动控制，在现实应用中，可以根据对喷管性能的实际需求选取合适的比例因子和非对称因子。

4 设计方法对比

4.1 典型截短设计方法

为证明本文提出的设计方法的优越性，本节将其与典型的喷管截短设计方法[13]进行对比分析。典型截短设计方法示意图如图14所示，其根据进出口条件设计完全膨胀喷管，并利用等比例截短方法使喷管满足几何约束，具体设计过程可见文献[13]。

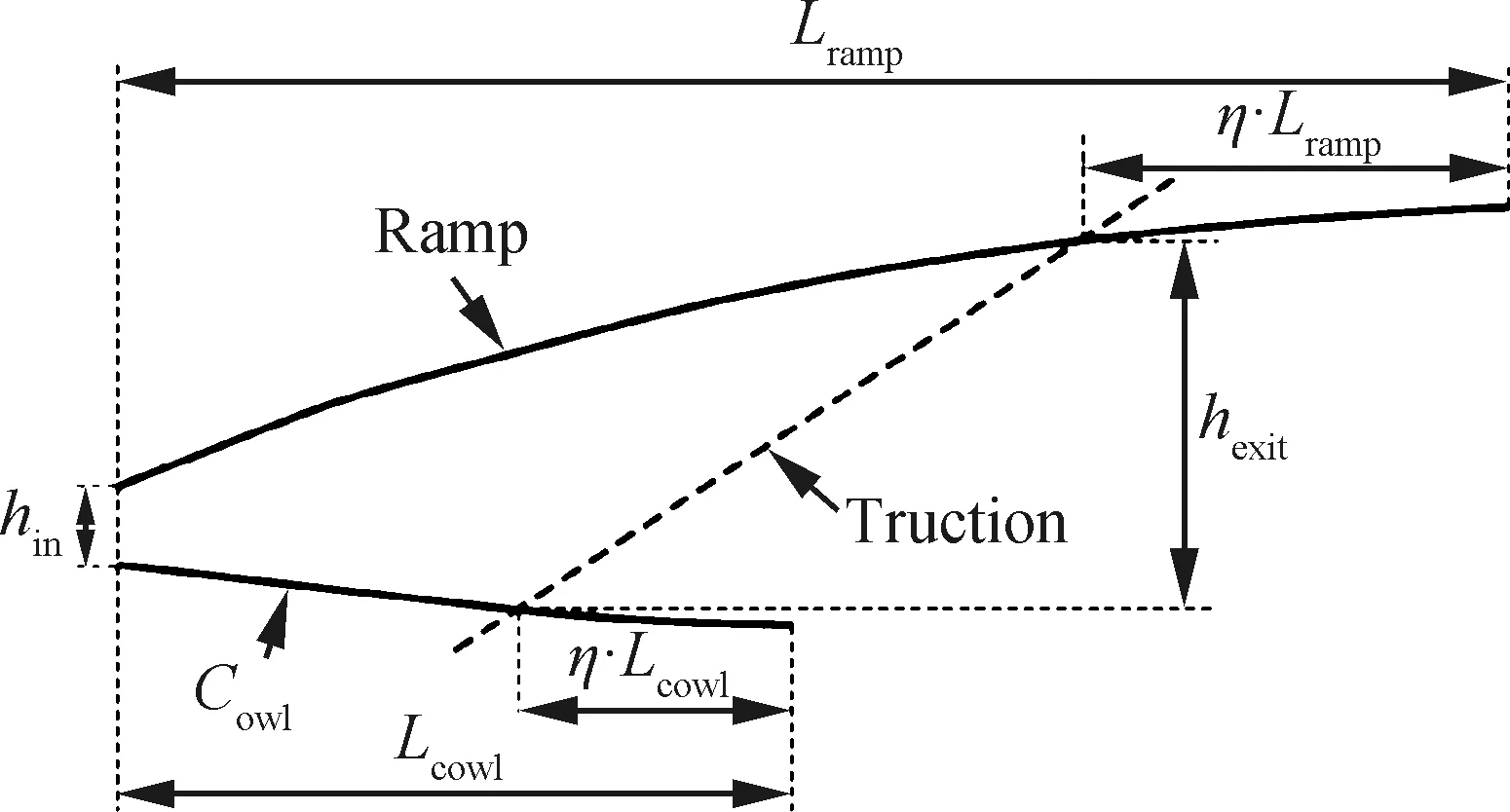
图14 典型截短设计方法示意图

应用截短设计方法设计喷管时，由于无法通过截短方法一次性获得满足高度和长度约束的喷管，因此首先根据长度约束进行等比例截短获得喷管6，其几何构型和流场结构可见图15，具体尺寸在表4中给出，其中Ln为喷管长度，Hn为喷管高度。可以看到喷管6的高度并不能满足约束条件。其次，根据高度约束进行等比例截短获得喷管7，可以发现此时喷管7的长度会小于长度约束。这从侧面再次说明截短设计方法并不能总是使喷管完全满足几何约束，并且可能会使部分尺寸过度截短，导致喷管性能恶化。

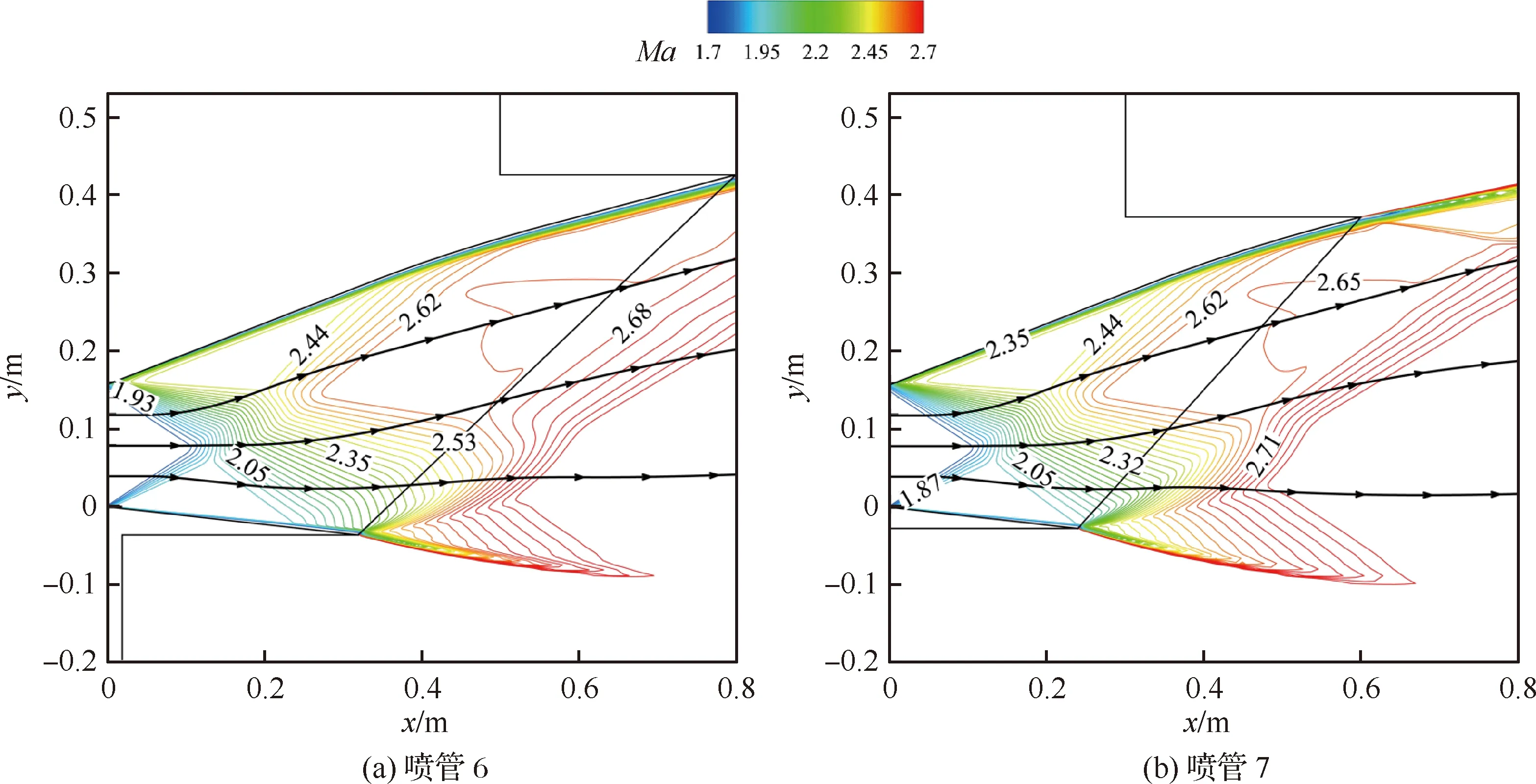
图15 传统喷管的马赫数云图

4.2 性能对比

根据2种截短条件得到的喷管性能参数在表4 中给出，同时给出了喷管2(由本文设计方法设计得到)的性能参数进行对比，表中ΔXn的定义为

表4 设计工况下喷管性能对比

(18)

式中：X为喷管的气动性能参数，可分别取Cfx、L和M，下标“n”为喷管序号。可以看到根据长度约束得到的喷管6的推力性能高于根据高度约束得到的喷管7的推力性能，这说明随着截短程度的增加，喷管的性能损失也随之增加。此外，相对喷管6，本文提出的设计方法得到的喷管2的推力系数和升力分别提高了11.95%和209.50%，俯仰力矩下降了3.02%。需要注意的是，喷管6的高度并不满足约束条件。而相对可以满足几何约束的喷管7，喷管2的性能提升更为显著，其推力系数、升力和俯仰力矩的增幅分别可达33.36%、265.75%和37.21%。

因此，本文提出的喷管设计方法不仅可以使喷管满足几何约束条件，并且可以有效提升喷管的气动性能。此外，通过调整比例因子和非对称因子可以实现对喷管推力和升力性能的控制，以满足实际应用中的需求。

5 结 论

本文提出了一种基于最大推力理论和特征线方法的几何尺寸约束的超燃冲压发动机喷管设计方法，该设计方法能够在满足尺寸约束的前提下优化喷管气动性能，并且可以通过调节比例因子和非对称因子来实现对喷管推、升力的控制。本文的主要结论如下：

1) 随着比例因子增加，喷管推力系数先增加再降低，升力和俯仰力矩逐渐增加，对于特定的设计工况和几何约束存在推力最佳的比例因子。随着非对称因子增加，喷管推力系数降低，升力和俯仰力矩逐渐增加，在非对称因子为1.0时，喷管推力系数达到最小值0.741，升力和俯仰力矩达到最大值，分别为3 009.97 N和2 154.46 N·m。

2) 相比典型的喷管截短设计方法，本文提出的设计方法不仅可以保证喷管满足几何约束，同时还能使其性能得到显著提升，喷管的推力系数、升力和俯仰力矩最高可提升33.36%、265.75%和37.21%。此外，在实际应用过程中可以根据不同的气动性能需求来调整比例因子和非对称因子，以获得满足不同性能要求的喷管。