基于FLAKNN的雷达一维距离像目标识别
2021-07-05韩磊周帅
韩磊, 周帅
(北京理工大学 机电学院,北京 100081)
高分辨距离像(high resolution range profile,HRRP)是用宽带雷达获取目标散射点子回波在雷达射线上投影的向量和,提供了目标散射点沿雷达径向距离方向上的分布情况,包含目标大量信息,具备易获取、占存储空间小等优势,成为雷达目标识别与分类领域的研究热点[1]. 随着机器学习算法的不断的发展,许多工作者将基于机器学习的分类算法应用于雷达识别领域,并取得了一定的进展[2-4].
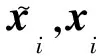
(1)
但是该算法有两个不足的地方:
① 在计算欧式距离时所有特征分量的权重相同,没有体现特征分量对分类的贡献作用.
②k值是一个全局固定的值,忽略了局部样本分布的情况.
针对第一个问题,为了提高各维特征的优势作用,刘先康等[5]提出了一种基于fisher判决率的近邻分类方法,对每一个特征分量进行加权计算,将特征分量的可分性作为加权因子,在训练集中寻找最近的一个样本,该算法利用特征的可分性增加了识别性能. 同样地,本文也从可分性出发,将所有特征分量投影至新的特征空间,使投影后的类别之间具备最大可分性;并且通过分析局部样本的分布情况最终决定测试样本的类别,以弥补k-近邻算法的第二个不足问题.
1 HRRP特征提取
1.1 HRRP数据特点
本文基于目标散射中心模型[6]对HRRP数据进行了仿真. 选用调频连续波雷达作为探测器,通过将回波信号与发射器发射的原始信号进行混频得到差拍信号,差拍信号包含目标距离、目标速度、目标形状等信息,然后将差拍信号进行傅里叶变换和频率-距离转换处理得到目标的 HRRP,它是目标散射点的子回波在探测距离方向上的矢量和.
仿真所使用的探测器主要的参数设置如表1所示,探测器参数的设定决定了探测器的距离分辨率、衰减等性能. 根据表1中主要参数进行仿真获得的一维距离像如图1所示. 当探测器处于目标不同的角度和位置时,其接获得的目标一维距离像也不相同,如图1中(a)和(b)所示分别为探测器相对目标距离相同,方位角分别为0°和14°时同一目标的高分辨距离像;图1(a)和1(c)为探测器相对目标方位角相同,距离分别为60 m和30 m时同一目标的高分辨率一维像. 可见,目标处于探测器不同位置和不同方位角时,其高分辨一维距离像的峰值数目和峰值所在的位置发生了改变,前者称为高分辨一维距离像的方位敏感特性,后者称为平移敏感特性. 为了解决强度敏感性问题,图1各图均做了归一化处理. 由于一维距离像具有以上敏感特性导致目标训练集的建立方法与常规机器学习中的不同,在制作目标的一维距离像训练样本集时,需要在不同角度和位置下提取目标的回波信号.
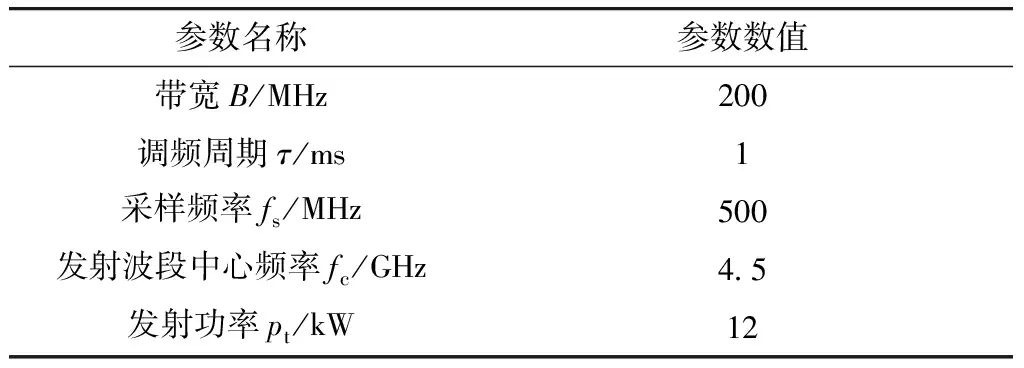
表1 探测器参数Tab.1 Parameters of the detector
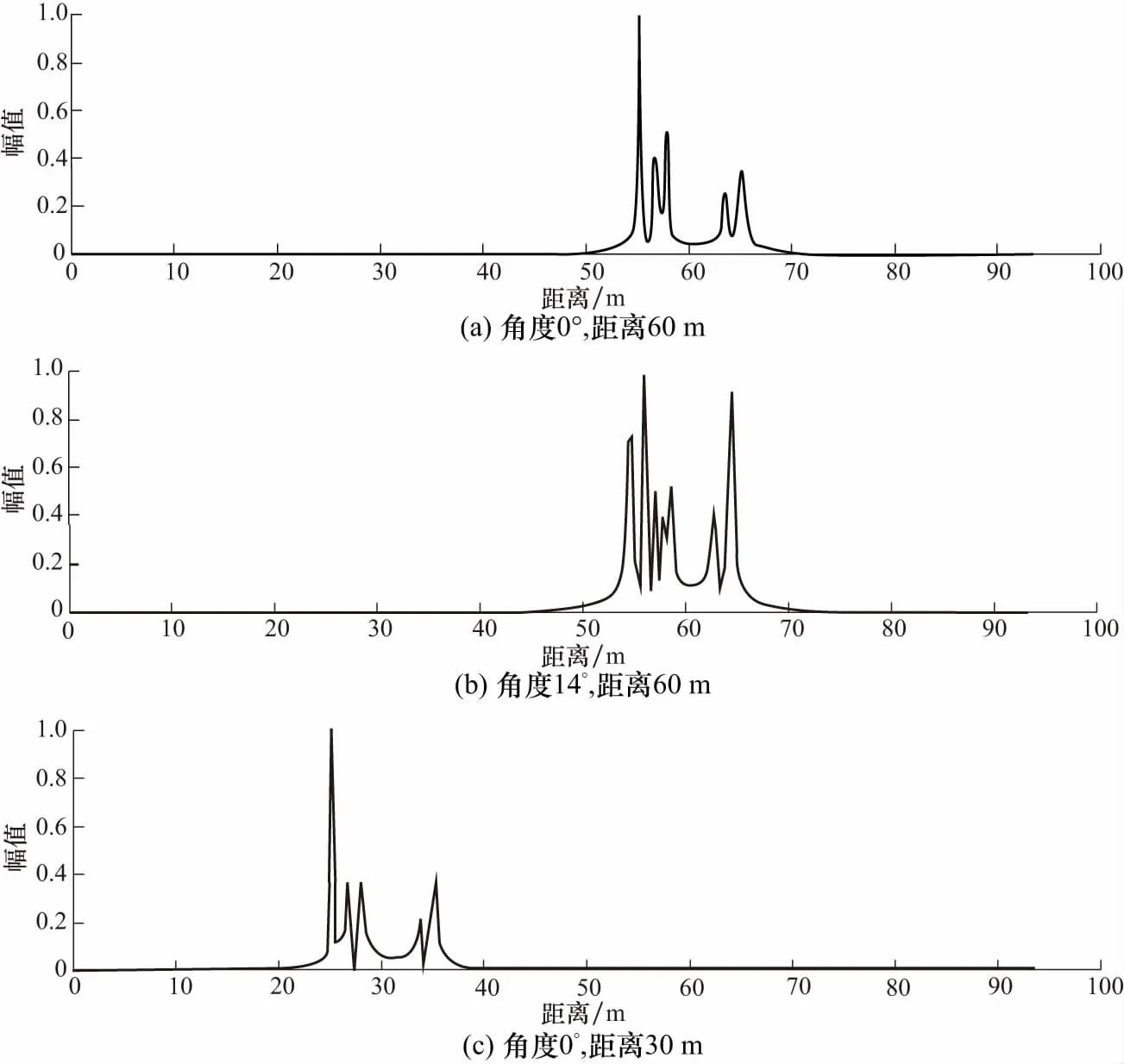
图1 同一目标不同位置、角度的HRRPFig.1 HRRP of the same target at different positions and angles
1.2 HRRP特征提取
在使用HRRP作为目标的识别与分类时,对目标特征的提取是对目标回波中明显的特征信息进行提取,是目标识别系统的关键步骤,直接影响分类的效果. 由于高分辨距离像存在姿态敏感、平移敏感和幅度敏感等问题使得同一目标在不同的情况下获得的距离像具有很大的差异. 因此对特征的提取提出了巨大的挑战,如何获取最小信息损失、高可分性且低维度的特征信息是提升分类器性能的关键[7-8].
距离像中峰值代表目标强散射中心的位置,为目标结构特征;距离像所占距离单元能够反映目标尺寸信息;目标的中心矩具有平移、旋转及尺度不变性[9-10],是常用于高分辨距离像模式识别的特征. 设第k次得到一组包含目标的一维距离像片段为x(k)={x1,x2,…,xN},xi为幅度归一化的数据,N为目标所占距离分辨率单元的总个数,则可以提取以下特征用于目标识别.
① 强散射点个数.
强散射点的个数是目标在雷达视线中反射回波能量比较大的点. 在文献[7]中强散射点的选取是通过与目标均值相比来获得,在文献[9]则是与最大的峰值的百分比相比获得,两者的判别式如下,区别在于阈值的选取不同.
T1=|{i||xk(i)>k*max(x)}|
or
(2)
式中:k为比例系数,k∈(0,1);|{. }|为集合元素的个数;mean(x)为均值;max(x)为x中最大值.
② 等效目标尺寸.
等效目标的尺寸反映了目标在不同的姿态角下的长度,在文献[8,11]中等效目标尺寸表示为第一强散射点的位置P(1)到达最后一个强散射点位置P(T1)的距离,代表了目标径向上的尺寸. 其定义式为
T2=P(T1)-P(1)
(3)
式中:T1为强散射点的总数;P(i)为第i个散射点所对应的距离. 由于HRRP随目标的姿态变化,等效目标尺寸也是随目标位姿变化而变化.
③ 整体熵分布.
熵能够反映目标散射中心分布的情况[8],分布比较散时其值较大,而分布较集中的时候其值较小. 其定义式为
(4)
熵值较大时,散射中心能量平均分布的可能性较大;反之,散射中心分布较为集中.
④ 标准差.
标准差能够反映目标散射中心偏离均值的程度[9,11]. 标准差越大,说明散射中心幅度较大,散射中心分布较散;标准差越小,说明散射中心分布比较均匀. 其定义式为
(5)
⑤ 不规则度.
不规则度反映了相邻三个点幅值大小的相对关系[11]. 其定义式为
(6)
规则度反映的是一种局部偏差,一定程度上能够表征物体的结构信息.
⑥ 径向能量.
一维距离像的的径向能量为幅度的平方和[9],径向能量特征的定义为
(7)
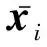
⑦ 对称度.
(8)
对称度反映了目标散射点散射截面积分布的对称程度[9],若T7=0,则目标距离像形状似梯形;若T7=1,则目标的距离像似“凹”或“口”;若T7≫1则似尖形.
⑧ 去尺度结构特征.
(9)
该特征只与距离像的波形内部有关,与尺度变化无关[9].
⑨ 二阶中心矩.
由于目标的散射点模型变化相对缓慢,距离像峰值位置变化也是一个缓变的过程,峰值位置相近的距离像具有相近的形状信息. 因而可以把中心矩作为距离像的特征[9]. 其中,二阶矩的定义式为
(10)

2 FLAKNN算法
FLAKNN算法的核心分为三个主要部分:① Fisher判别分析[12]:该算法是特征降维领域常用的算法,主要思想是寻找一个低维的超平面,经过投影所得的特征在该超平面上能够实现类间特征中心距离最大,类内特征的方差最小,使投影后不同的类别之间具备最大可分性. ② 局部分析:根据测试样本的局部情况进行分析,从相邻样本的数量及同一类别的中心样本与测试样本的距离两个方面来决定测试样本的归属. ③k值调整:使用交叉验证的方法确定全局最优以及一系列较优的k值,并在局部分析过程中遍历这些值,最终使用少数服从多数的投票法则决定测试样本的类别.
2.1 Fisher判别分析
假设有k个类别y={c1,c2,…ck},每个类别的样本为Xk={x1,x2,…xn},其中xi为m维向量,表示特征的m维分量. 若投影的低维空间为d维,对应的基向量为(w1,w2,…wd),由基向量组成的矩阵为W,W∈Rm×(k-1).
Fisher判别分析面向多分类问题时其目标优化函数为:
(11)
式中:tr(·)表示对角元素的乘积;Sb为类间散度矩阵;Sw为类内散度矩阵,计算方式如下式所示:
(12)
(13)
式中:μ为全部样本各维的均值;μi为第i类样本各维的均值.
该算法的具体步骤如下:
第1步:计算不同类别样本各个维度的均值μi及全部样本各维的均值μ;
(14)
(15)
第2步:根据式(12)、(13)分别计算类内散度矩阵Sw和类间散度矩阵Sb;
第4步:构成投影矩阵Wd×m,投影矩阵Wd×m用数学公式表达为
(16)

(17)
(18)
2.2 局部分析(local analysis )
传统KNN算法通过少数服从多数的原则确定测试样本的类别. 如图2所示,横轴坐标表示归一化后的特征值,若k值设定为14,通过计算测试样本与所有训练样本的欧式距离,从中选出距离最近的14个样本,从图中可见c1类别的个数为5,c2类别的个数为8,c3类别的个数为1,根据少数服从多数的投票原则,该测试样本应该归属于c2类别. 但是根据局部的分布情况,该测试样本更有可能属于c1类别. 因此,传统KNN算法仅通过设定全局最优k值在面对一些特殊的情况下会出现误判的情况,导致分类器识别性能下降. 因此,本文算法结合局部样本的分布和类别的个数综合来决定测试样本的类别.
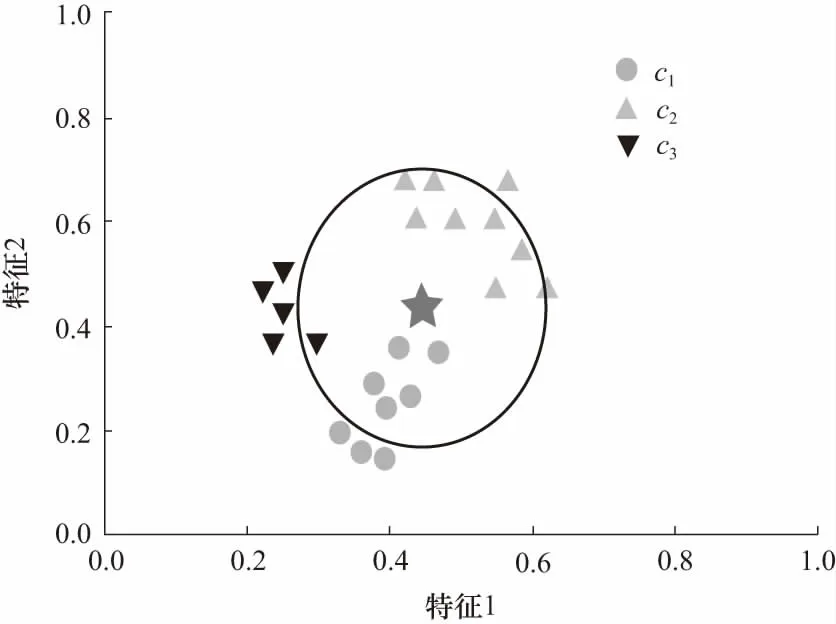
图2 局部分布情况图 Fig.2 Local distribution
局部分析算法步骤如下:
第1步:计算测试样本x′与所有训练样本X′的欧式距离.
第2步:将距离进行从小到大排序,取前k个样本对应的位置和标签,并统计相同类别的个数,ci表示的是类别,numi表示的是该类别在前k个距离最小样本中相同类别的个数.
info_knn={(c1,num1),(c2,num1),…,(ck,num1)}
(19)
第3步:计算每个类别在前K个距离最小样本中所占的比例.
ri=numi/k,i={1,2,…k}
(20)
根据该比值的大小分以下几种情况进行讨论:
① 当r≥γ时,其中γ为预先设定的阈值且γ∈(0,1],表示该类别占绝大多数,这里可调整γ值,当r越接近1时表该类别占据主导判别地位,使用少数服从多数的原则将该测试样本归类为占比最多的类别.
② 当r<γ,表示其他的类别与该类别地位相当,该类别不具备主导判别的地位. 此时考虑所有的类别的分布情况,在文献[13]仅仅考虑了第一和二大类别的分布,忽视其它个数少的类别的作用. 本文考虑前k个中所有类别分布情况,并构建一个判别式进行测试样本的判别. 首先,计算同一类别特征分量的中心,以该中心值重新计算与测试样本的欧式距离(d1,d2,…,dk),重新比较距离的大小,将距离和个数构成如下判别式,将该判别式输出最大值的类别视为该测试样本的最终类别.
c={ci|i=max(ri+1/di),i=1,2,…,k}
(21)
2.3 k值调整策略(adjustment strategy of k value)
k值大小直接决定了分类器的识别性能,选用小的k值,学习近似误差会减小,但是学习的估计误差会增大,此时容易发生过拟合;选取较大的值,可以减小学习的估计误差,但会使学习的近似误差增大[14]. 在2.2小节中通过局部分析的方式,综合类别所占比例和距离综合判别测试样本的归属,然而k值是在全局仍然是一个定值. 传统KNN算法可通过交叉验证的方法确定这个全局最优的k值,但对于一些混叠的区域,不同类别的特征分布混叠在一块,在这些地方传统KNN算使用固定的k值不能够正确的将测试样本进行归类,需要一种方式来调整k值的大小,再根据测试样本所处的空间位置根据具体的情况具体进行判断.
本文针对这一问题,通过局部调整k值,结合2.2节局部分析的方法,统计一定范围内对应k值的判别结果,最终对所有判别的结果进行投票,票数最多的判为测试样本的最终类别.k值调整算法具体步骤如下:
第1步:通过k折交叉验证的方法确定一定范围内k值对应的准确率.
第2步:将准确率按从大到小得顺序排列,选择准确率最高的前q个对应的k值.
第3步:对每一个测试样本遍历k值的取值并记录每一个k值的判别结果. 每个k值对应的判别结果由局部分析得出,结果如下所示,其中numi表示对应类别ci判别结果相同的次数.
{c1:num1,c2:num2,…,ck:numk}
(22)
第4步:投票. 每个判别结果出现的次数代表所得的票数,取得票数最多的类别为测试样本的最终类别.
3 实 验
3.1 目标回波与特征提取
为了验证算法的有效性,仿真了三个尺寸、形状不同的物体目标所对应的一维距离像. 图3所示为目标距离探测位置均为60 m时目标的一维距离像,不同目标的一维距离像存在很大的差异.
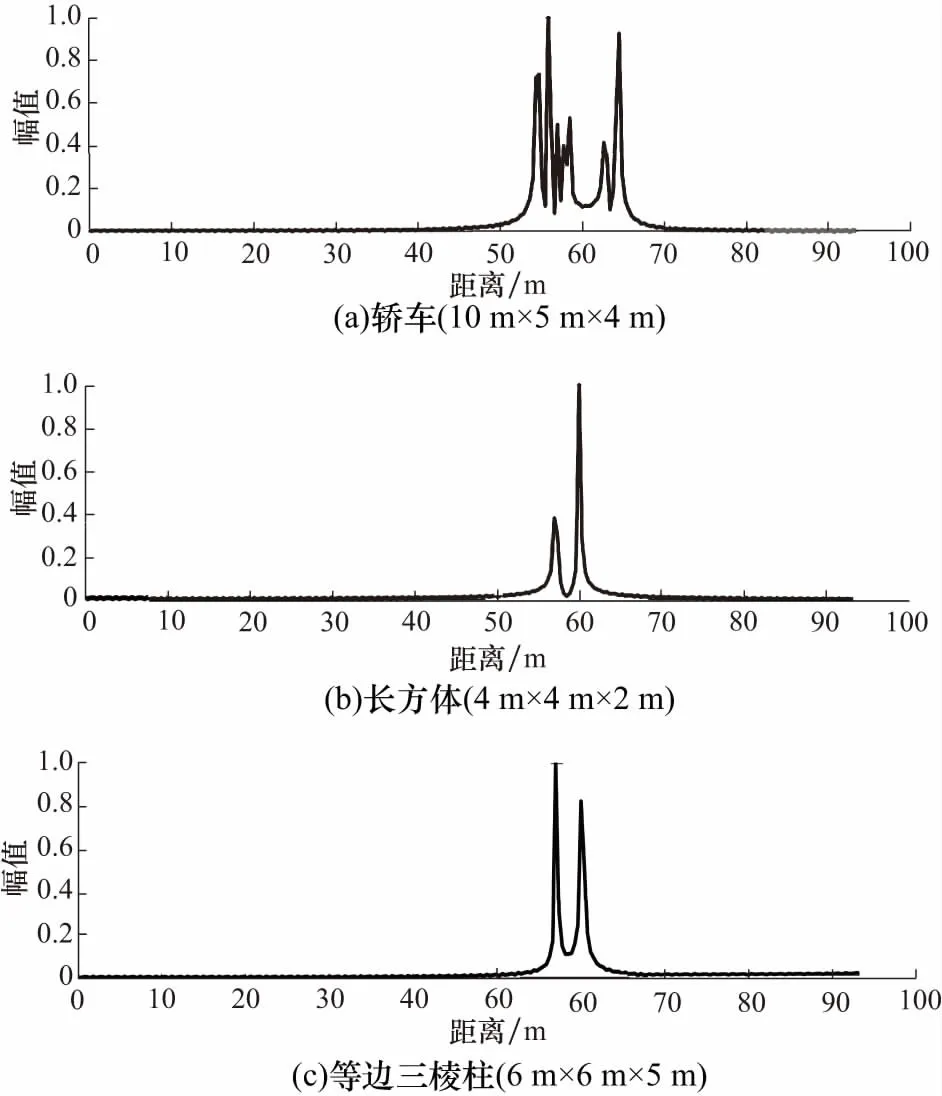
图3 不同目标的HRRPFig.3 HRRP of different targets
为了减小姿态敏感的影响,根据文献[15]每隔5°采集了这三类目标的回波,将回波数据进行预处理后,对含有目标的一维距离像进行特征提取,得到目标的训练集,大小为72×9×3. 图4展示了部分特征值提取结果,从单个特征维度上来看,不同目标的特征存在相互重叠的部分,这表示在某些位置不同目标的一维距离像存在相似性,仅从单个特征无法将目标进行准确分类.
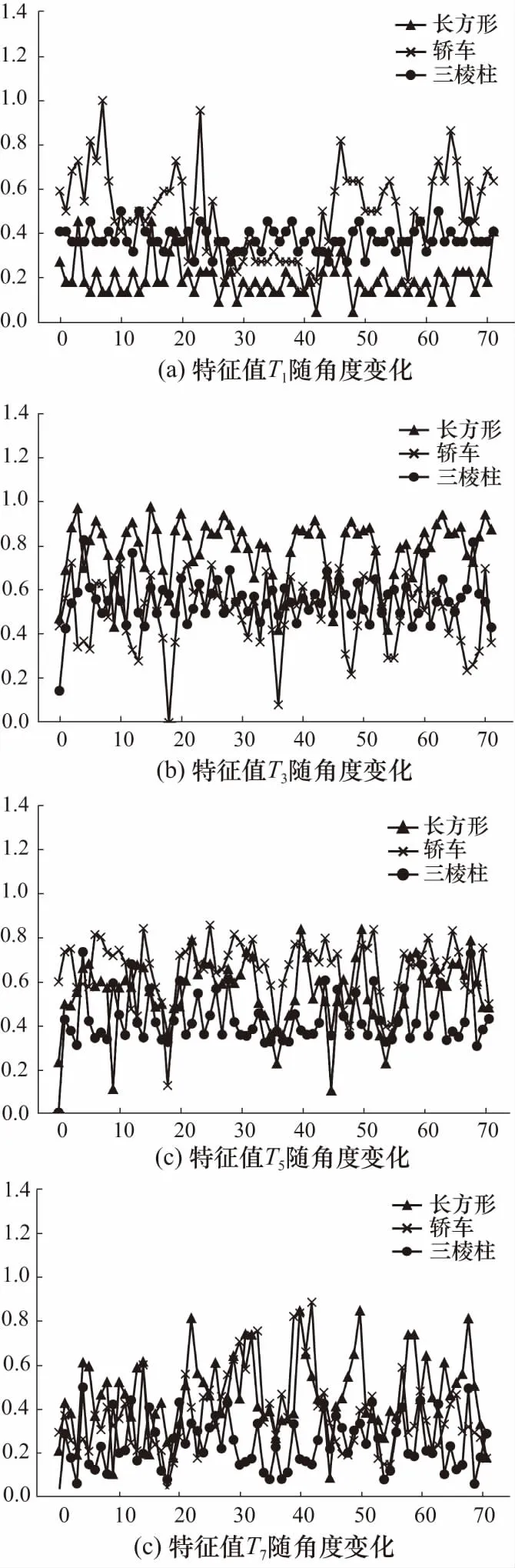
图4 不同目标特征值分量随角度变化情况Fig. 4 Variation of eigenvalue components of different targets with angles
根据机器学习算法的流程,识别的过程分为训练阶段和测试阶段,两个阶段使用样本依据互斥的原则[16]制作样本集.
训练阶段:每个目标将其角域分成72等分,即隔5度测量一次回波数据,训练集的大小为72×9×3.
测试阶段:对于3个目标在其角域内随机测量50组回波数据,测试集的大小为50×9.
3.2 数据处理与分析
为验证所提算法的目标识别效果,利用仿真数据进行了具体的实验. 实验数据处理环境采用的是window 10 ,CPU型号为Intel(R)Core(TM) i7=4 720HQ CPU @2.60 GHz 2.59 GHz. 按照第3节中算法的原理,为与传统的KNN算法对比,首先经过交叉验证确定全局最优的k值,交叉验证的结果随着k值的变化如图5所示.

图5 准确率随k值变化曲线Fig.5 Change curve of accuracy with k value
从该图确定全局最优的k为5,在k值调整算法中定义k的取值为{2,4,5,6,7},测试样本从三类目标5°角域内任意一个角度,组成一个50×9的测试集,保证测试样本不会出现在训练样本集中. 重复进行20次实验,实验结果如表2所示.
由表2计算可知传统KNN算法的识别准确率平均值为0.954,基于Fisher判别率加权的最近邻分类器的识别准确率平均值为0.967,算法FLAKNN算法的准确率为0.974.可见改进算法加权最近邻和FLAKNN算法的识别性能均高于传统KNN算法.

表2 三种算法的准确率(5°)Tab.2 Accuracy of the three algorithms (5°)
为了探究角域划分间隔的影响,将间隔角度逐次增加5°,直至将角域间隔增加至30°. 重复上述目标识别实验,并求得在对应角域间隔下各个算法的平均准确率,得到三种算法的准确率随角域间隔变化的图像,如图6所示.
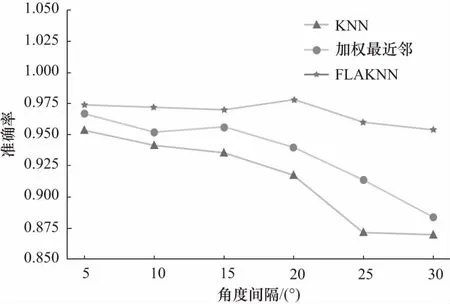
图6 准确率随角域间隔变化曲线Fig. 6 Variation curve of accuracy with different angular gap
由图6可见,随着角域划分间隔的增加,三种算法的平均准确率均有下降的趋势,且随着角域划分间隔的增加,准确率下降越快. 其中,传统KNN算法的准确率下降最快,其次是加权最近邻算法. 而FLAKNN算法的识别准确率下降得最慢,且当角域间隔增加至30°时,平均识别准确率为0.954,仍保持了较高的识别率,其他两者的准确率分别为0.870和0.884,相较角域划分间隔为5°时,识别率分别下降了8.4%和8.3%.
由此可见,所提出的FLAKNN算法进一步提高了基于一维距离像的目标识别效果.
4 结 论
针对传统KNN算法进行一维距离像目标高分辨分类时所存在的不足,提出了一种FLAKNN的目标识别方法.首先,使用Fisher判别分析,将高维空间中的特征分量线性投影到低维空间,投影后类间中心距距离最远,类内方差最小,实现不同类别间最大可分.对于每一个测试样本,根据其所处的局部情况,在相邻k个样本出现多个类别且第一大类别不占主导判别地位时,考虑每个类别的中心与测试样本的距离,根据所占个数和距离综合决定测试样本的类别,并同步调整k的取值,最终使用少数服从多数的投票法则决定测试样本的类别.将该改进算法应用于基于高分辨一维距离像目标识别,结果表明,FLAKNN的识别性能优于传统KNN算法,并且在传统KNN识别率下降的情况下,仍保持了较好的识别性能,因此,所提算法进一步提高了雷达一维距离像的目标识别效果.
