基于改进的集合经验模态分解的爆破振动信号趋势项消除方法

李晨， 梁书锋， 刘传鹏， 程健， 刘殿书

(中国矿业大学(北京) 力学与建筑工程学院，北京 100083)

在各类爆破的振动测试过程中，由于测振仪器本身性能、安装方法以及环境条件等因素的影响，振动测试结果中时常存在具有长周期特征的趋势项. 趋势项是振动信号波形偏离基线中心的现象[1]. 而受其影响，信号时程曲线波动特征的准确性和频谱分析的分辨率将大大降低[2].

以往趋势项的消除方法主要有平均斜率法[3]、最小二乘法[4]和小波分解法[5]等，而限于其需要一定的先验知识，这些方法逐渐被具有自适应性的经验模态分解(empirical mode decomposition，EMD)法所取代[6]. 在此基础上，为了抑制EMD法在实际应用过程中出现的模态混叠现象，学者们随后提出了集合经验模态分解(ensemble empirical mode decomposition，EEMD)法并将其用于信号趋势项的消除[7]. 然而，EEMD法虽然在一定程度上抑制了模态混叠、提高了固有模态函数(intrinsic mode function，IMF)分量的提取精度，但其同时增加了由添加白噪声引起的重构误差，甚至出现了模态分裂等问题[8].

综上所述，文中拟采用改进的集合经验模态分解(modified ensemble empirical mode decomposition，MEEMD)方法，并依据趋势项成分的相关识别参数，确定适用于爆破振动信号的趋势项消除方法.

1 趋势项消除方法

1. 1 MEEMD方法的分解步骤

MEEMD方法[9]是在EEMD方法的基础上结合排列熵[10]的随机检测提出的，其分解步骤可归纳为：

(1)

式中:ai为添加的第i列白噪声信号幅值，一般取原信号x(t)标准差的0.1～0.2倍；N为添加的白噪声对数，选择百以内即可.

(2)

式中:j为IMF分量按高频到低频排列的序号；m为EMD分解尺度.

(3)

④ 计算各cj(t)排列熵值Hj，并依次判断Hj是否大于阈值θ0(一般取0.6). 如果排列熵值Hj大于θ0，则对应的cj(t)为异常分量，且继续检测下一分量的排列熵值Hj+1，直至某一分量cp(t)不是异常分量. 此时将前p-1个分量从原信号x(t)中分离出来，即：

(4)

⑤ 最后对剩余分量r(t)再进行EMD法分解，将得到原信号x(t)按高频到低频排列的所有IMF分量.

1.2 趋势项判别方法

针对上述MEEMD法分解得到的各IMF分量(包括余项)，需要准确识别哪些分量是趋势项的有效组成部分. 目前的识别方法有均值比法[11]、相关系数法[12]和频谱分析法等，其中频谱分析法需要长期观测经验或人工判别，不利于自适应分析，而相关系数法的识别标准尚未一致[13]. 因此文中采用均值比法对得到的各IMF分量进行识别.

① 分别计算原信号x(t)和各IMF分量的均值E(x)和E(Cl)：

(5)

(6)

式中:tk为第k个采样点对应的时刻；L为信号采样长度；Cl(t)为x(t)经MEEMD分解得到的第l个IMF分量序列；h为MEEMD分解尺度.

② 计算各IMF分量和原信号的均值比ξl

ξl=E(Cl)/E(x)

(7)

③ 基于趋势项长周期特征，从最后一列IMF分量开始，反向依次判断累计均值比S是否大于0.95[11]，累计均值比S可由下式计算

(8)

式中:q初始值为h，如果S小于0.95，则q=q-1，代入式(8)继续判断，直至S大于0.95判定结束. 此时第q至第h列IMF分量之和为提取的趋势项T(t)，即

(9)

2 仿真计算

利用Matlab对上述基于MEEMD的趋势项消除方法进行仿真. 在仿真计算中，鉴于爆破振动信号的强度-频率非平稳特性，构造采样频率512 Hz、采样长度1 024的调幅-调频信号s1如式(10)，其波形如图1所示.

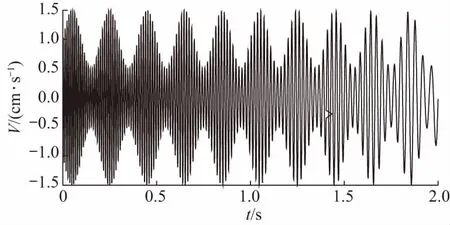
图1 s1信号波形图Fig.1 Signal wave form of s1

s1=(1+0.5sin 10πt)[sin(-40πt2+200πt)]

(10)

另外考虑到爆破振动的分段起爆特性，根据s1信号构造间歇振动信号s2，如图2所示.

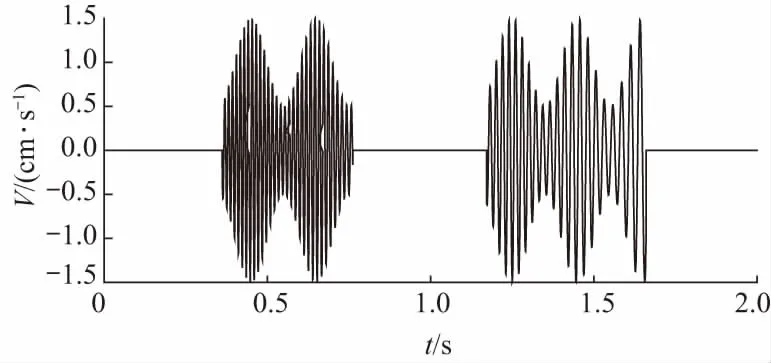
图2 s2信号波形图Fig.2 Signal wave form of s2

对于趋势项信号，由于其在实际测试过程中较为复杂，通常包含多种类型的趋势项[11]，因此构造复合趋势项信号d(t)为

d(t)=3e-1. 4t-0.02t3-0.5t2+2t-2.5

其中包括线型、多项式型和指数型3类工程中常见的趋势项，如图3所示.

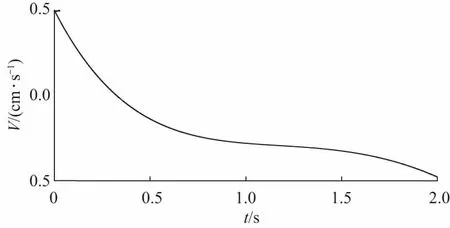
图3 趋势项信号波d(t)形图Fig.3 Signal wave form of trend terms

将趋势项信号添加至信号s1和s2，得到振动模拟信号x1和x2. 分别对x1和x2进行MEEMD分解(如图4所示)，并计算各IMF分量与其原信号的均值比，结果列于表1. 依据均值比法的判定标准，两列模拟信号分解后末尾分量的均值比均大于0.95，可判定末尾分量即为待提取趋势项. 图5为上述方法与分别基于EMD和EEMD的趋势项消除方法对趋势项信号d(t)的提取结果图.

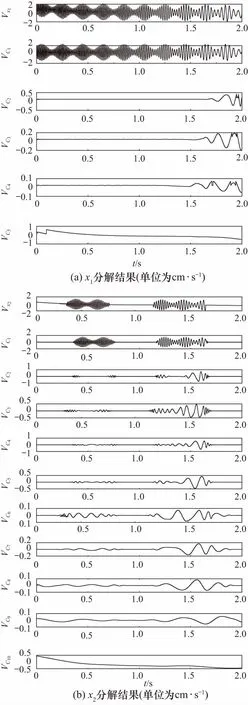
图4 MEEMD法分解结果Fig.4 Decomposition results by MEEMD

表1 各IMF分量与其原信号的均值比

图5 模拟信号趋势项提取结果Fig.5 Extraction results of simulate signals trend terms

由图5可以看出：对于持续振动信号x1，三种方法对趋势项的提取结果较为接近，并与趋势项信号d(t)的一致性均较好；对于呈间歇振动的信号x2，三种方法对趋势项提取结果相差较大，且基于EMD的趋势项消除方法无法有效提取趋势项信号d(t). 为了对比基于EEMD的趋势项消除方法和文中方法对信号x2中趋势项的提取效果，分别计算二者提取结果与趋势项信号d(t)的相对范数、均方根误差和最大误差[7]，如表2所示. 由表2可知：文中方法相较前者在相对范数、均方根误差和最大误差上分别降低了约60%、47%和68%，对趋势项信号d(t)的提取更为充分.

表2 两种方法的趋势项提取效果比较Tab.2 Trend terms extraction effect caused by different methods

综上所述，当测试信号呈间歇振动时，应优先选取文中方法进行信号的趋势项消除. 因此，鉴于爆破振动的分段起爆特性，该方法对爆破振动信号中趋势项的消除具有更强的适用性和更大的优越性.

3 实例分析

以京张高铁八达岭车站掘进时的某次爆破振动速度信号为例，验证文中方法在实际工程中的可靠性. 实测爆破振动速度信号为多段导爆管雷管起爆下的测试结果，其采样频率2 000 Hz，由于测试仪器对低频(小于5 Hz)振动的非线性响应，导致信号中出现明显趋势项成分，不仅使得信号时程曲线偏离基线中心，而且频谱图中主频异常(0～2 Hz范围内出现超高幅值的低频分量)，如图6所示.

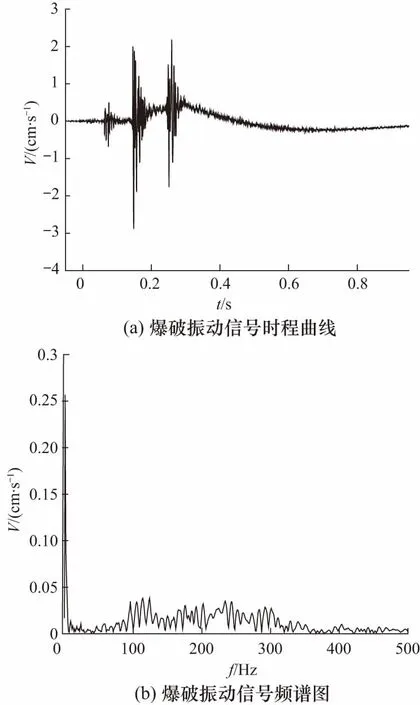
图6 实测爆破振动信号及其频谱图Fig.6 Measured blasting vibration signal and its spectra

对实测信号进行MEEMD法分解，得到8个IMF分量(包括余项)，结果如图7所示.

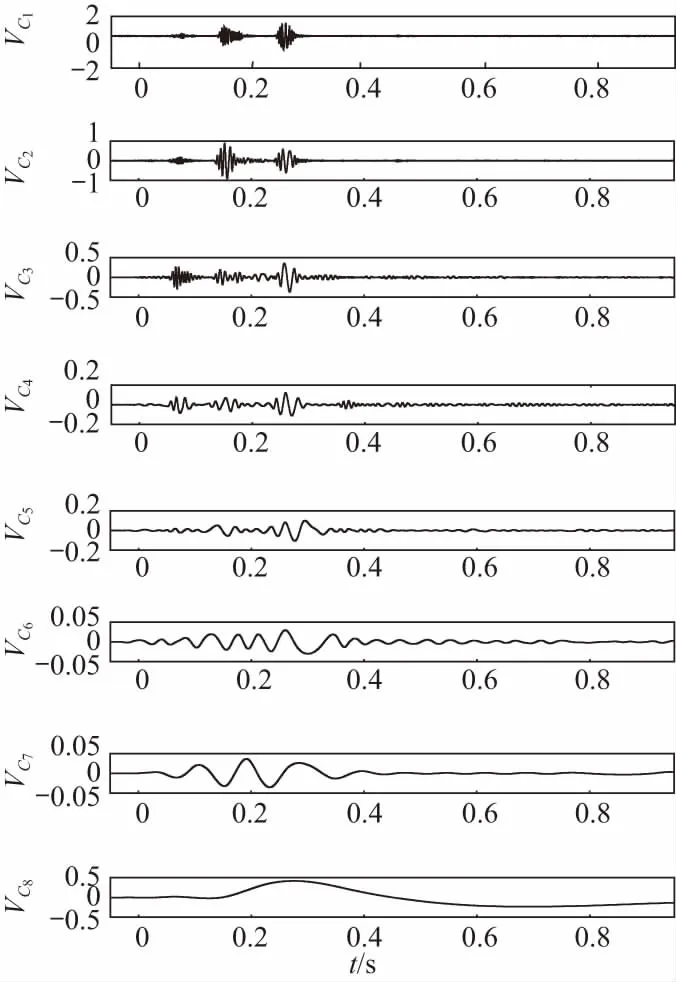
图7 实测信号分解结果(单位为cm·s-1)Fig.7 Decomposition results of measured signal(unit:cm·s-1)

各IMF分量与实测爆破振动信号的均值比如表3所示. 依据表3中的计算结果和均值比法的判定标准可知末尾分量为待提取趋势项，消除趋势项后可得到修正后的振动速度信号，如图8所示.

表3 各IMF分量均值比

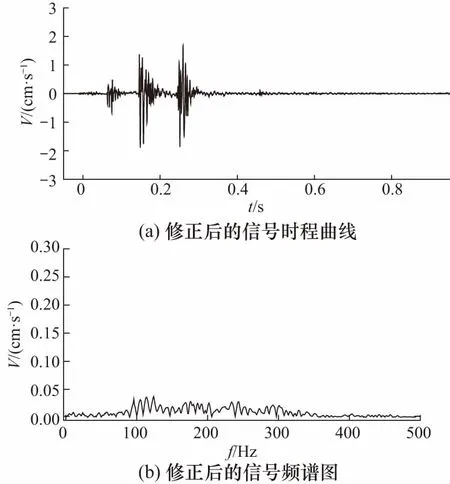
图8 修正后的信号及其频谱图Fig.8 Corrected signal and its spectra

从图8可以看出振动信号回归到基线中心、频谱图中低频响应现象[14]消失，此时信号FFT主频计算结果为124 Hz，趋于合理.

4 结 论

文中基于MEEMD提出一种信号趋势项消除方法，通过模拟信号的仿真计算和爆破振动信号的实例分析得出以下结论.

① 对于持续振动的模拟信号，文中方法与分别基于EMD、EEMD的趋势项消除方法对信号中趋势项的提取效果较为接近，且与实际趋势项的一致性均较好.

② 当测试信号存在间歇振动时，基于EMD法趋势项消除方法已无法有效提取趋势项，而文中方法对模拟信号的趋势项提取结果相较于基于EEMD分解的趋势项消除方法在趋势项信号相对范数、均方根误差和最大误差方面分别降低了约60%、47%和68%，对趋势项信号的提取更为充分，体现了其对分段爆破振动信号中趋势项消除的优越性和适用性.

③ 对于实测爆破振动信号，文中方法有效消除了信号中由于低频响应导致的趋势项(0～2 Hz内低频分量幅值超高)，使时程曲线重回基线中心，修正后信号主频为124 Hz，提高了信号频谱分析结果的准确度，验证了文中方法在实际应用过程中的可靠性.