地基GNSS-R功率测量应用中的天线方向性影响分析

洪学宝， 张波, 杨东凯, 汉牟田

(北京航空航天大学 电子信息工程学院，北京 100091)

全球导航卫星系统(global navigation satellite system, GNSS)反射信号测量技术(GNSS reflectometry, GNSS-R)是利用地球表面反射的GNSS信号进行地物参数遥感的一种技术手段[1]，能够工作在地基、空基和星基3种场景下，可以满足不同的观测尺度需要，已被广泛应用于区域甚至全球范围的地物参数遥感中.

GNSS-R典型观测量为反射信号的时延多普勒图(delay Doppler map，DDM)，本质为经由目标面反射的GNSS信号的非相干积分值[2]. 在反射面粗糙度较低的情况下，反射信号DDM峰值与镜面反射点附近反射的信号绝对功率相关[3]，可以用于与反射面介电特性相关的参数遥感，如土壤湿度[4]、海冰[5]和海面溢油[6]等，本文将这类遥感应用统称为GNSS-R功率测量应用.

天线方向性表示天线在不同方向对电磁波的辐射或接收的能力，是影响天线性能的重要因素，实践中常以天线方向性系数和天线增益来定量描述，其中后者为前者与天线效率的乘积[7]. 在GNSS-R功率测量应用研究中，一般假定直射和反射信号接收天线具有理想的方向性，即仅接收来自天线前向的同极化信号. 然而，实际应用中的天线方向性并不理想，在接收目标信号的同时也可以接收到同极化和交叉极化的GNSS干扰信号[8]. 地基平台下，干扰信号与目标信号的载波频差和传播延迟几乎可以忽略，这会造成目标信号尤其是反射信号的相关功率(非相干积分值)偏差，对后续的参数反演形成不良的影响[9-10]. ZAVOROTNY V U等[11]中讨论了目标信号为直射信号时非理想RHCP天线接收的信号表达，WAN W等[12]在GNSS-R数据处理过程中利用多项式拟合进行了非理想RHCP天线接收的直射信号校准，但是天线方向性对于目标信号尤其是反射目标信号相关功率测量的影响并未得到充分讨论.

本文将以典型的RHCP直射信号接收天线和LHCP反射信号接收天线的组合为例，建立地基情况下两天线接收信号相关功率模型，确定两天线接收信号相关功率的概率分布和典型数字特征，在仿真的基础上以相对偏差和离散系数对天线方向性造成的信号相关功率测量系统误差和随机误差变化进行定量分析.

1 相关功率的数学表达

地基GNSS-R几何关系如图1所示. 其中RHCP天线用以接收直射信号，最大增益方向指向天顶；LHCP天线用以接收反射信号，最大增益方向指向天底. 两天线相位中心连线与地面垂直，LHCP天线相位中心距离地表高度H，RHCP与LHCP天线相位中心高度差为h，卫星高度角为θ.

图1 地基GNSS-R几何关系Fig.1 Geometry of ground-based GNSS-R

在地基遥感应用中，天线相位中心与地面距离不大，可以进行如下近似：(1)相对于可见星而言，抵达天线和镜面反射点的直射信号具有几乎相同的传播距离和发射角度，根据电磁波传播理论可以认为抵达天线和镜面反射点的直射信号具有相同的功率密度；(2)相对于可见星而言，两天线和镜面反射点具有几乎相同的位置和速度，根据多普勒效应原理可认为抵达天线和镜面反射点的直反信号具有相同的载波频偏. 考虑同极化及交叉极化天线方向性，t时刻RHCP天线与LHCP天线接收的信号表达如下.

(1)

式中：u为信号；n为加性噪声；下标r和l分别表示RHCP天线和LHCP天线；R和L分别表示RHCP信号和LHCP信号；上标+和-分别表示从天线正向和背向入射. 假定地面平整，反射信号可认为是直射信号的单多径，那么式(1)中的各信号成分可以表示为[13]

(2)

式中：P0为RHCP天线单位增益方向接收到的直射信号功率；G为天线增益；D为导航电文；C为伪随机噪声(pseudo-random noise，PRN)码；f0为载波频率；φ0为载波初始相位；|ΓRR|和φRR分别为右旋入射右旋出射时反射系数ΓRR的模值和相角；|ΓRL|和φRL分别为右旋入射左旋出射时反射系数ΓRL的模值和相角；Δτ1=2(H+h)sinθ/c为RHCP天线接收到的反射信号与直射信号之间的时间延迟[14]；Δτ2=hsinθ/c为LHCP天线接收到的直射信号相对于RHCP天线接收到的直射信号之间的时间延迟；Δτ3=(2H+h)×sinθ/c为LHCP天线接收到的反射信号与RHCP天线接收到的直射信号之间的时间延迟，这里c为真空中电磁波传播速度. 反射系数可以用反射面相对复介电常数ε和卫星高度角θ表示如下[15].

(3)

GNSS信号为直接序列扩频信号，接收完成后需要对两路信号分别进行相关处理[16]

(4)

式中：Y表示相干积分值；t0为积分起始时刻；Tc为相干积分时长；a为本地产生的伪随机噪声码序列；e为自然对数底；j为虚数单位；f0和φ0分别为本地生成的载波频率和初相.

本文旨在讨论天线方向性的影响，可以假定右旋圆极化天线接收的直射信号完全同步，即直射信号的载波频率跟踪误差、载波相位跟踪误差以及伪码跟踪误差均为0. 地基场景中天线架设高度较低，可以认为反射信号的载波频率和伪码相位也完全同步，并且同时刻不同信号分量具有相同导航电文，如此可得到k时刻两路相干积分值的表达.

(5)

式中：X为相干积分后的复加性噪声；Δφi=2πf0Δτi(i=1,2,3)为RHCP天线接收的直射RHCP信号与其余各信号成分传播路径差造成的相位变化量.

为了进一步提升观测序列的信噪比，GNSS-R信号处理过程中一般会对相干积分值进行非相干累加，得到k时刻两路信号的相关功率为

(6)

其中，Mic为非相干累加次数.

将式(5)代入式(6)，可得地基条件下的GNSS-R功率测量应用中实际天线接收信号相关功率的数学表达.

(7)

由上述表达可见，实际天线接收到的信号不仅包含目标信号，还包含由于背向抑制和交叉极化抑制的不理想引入的干扰信号，以实际信号相关功率作为目标信号相关功率的观测值会引入测量误差，本文接下来将对此进行分析.

2 相关功率的概率分布和数字特征

由于随机噪声的存在，信号相关功率序列为一个离散时间随机过程. 由于期望可以反映相关功率的平均波形，而方差可以反映相关功率的随机特性，本节将首先确定相关功率的概率分布，在此基础上计算相关功率的期望和方差.

(8)

式中：μr和μl分别为直射和反射通道信号复相干积分值期望的模的均方值；Ix(·)为第一类x阶修正贝塞尔函数. 假定非相干累加过程中各信号幅度变化足够小，有

(9)

这里，

(10)

根据非中心卡方分布的性质，可以得到两路信号相关功率的期望mr和ml为

(11)

(12)

3 基于数字特征的天线方向性影响仿真分析

本文以GPS L1(1 575.42 MHz)C/A信号为例对实际信号相关功率的数字特征进行了仿真，进而对天线方向性带来的目标信号相关功率测量误差进行定量分析. 仿真中，反射面相对介电常数为5，天线单位有效面积接收直射信号功率为-160 dBW，噪声频谱密度-204 dB/Hz，相干积分时长为1 ms，非相干累加次数为1 000次，接收机截止高度角为5°. 所用RHCP天线和LHCP天线相位中心距离反射面高度分别为2.05 m和1.95 m，忽略两天线彼此间的影响以及架设设施对两天线的影响，图2给出了两天线的主极化和交叉极化增益分布，其中实线代表RHCP天线的RHCP增益分布和LHCP天线的LHCP增益分布，虚线代表RHCP天线的LHCP增益分布和LHCP天线的RHCP增益分布.

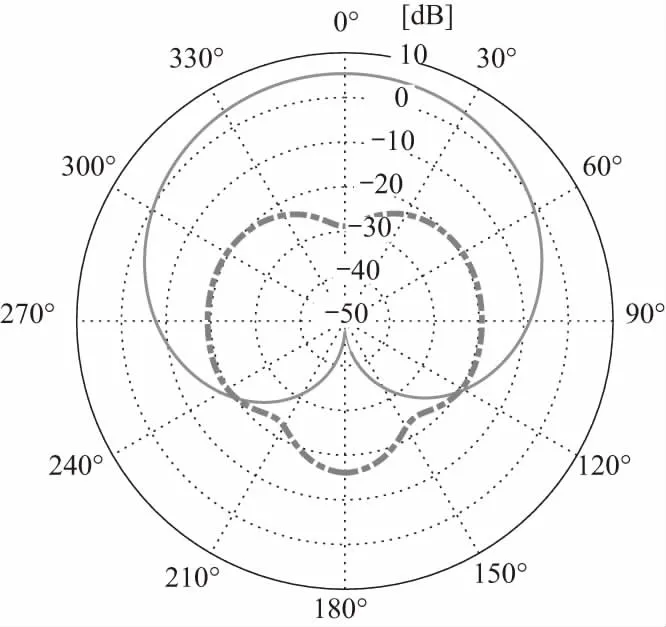
图2 天线增益分布[17]Fig.2 Antenna gain pattern[17]

3.1 系统误差分析

信号相关功率测量的系统误差表现为实际信号相关功率期望与目标信号相关功率期望之偏差. 定义相关功率测量的相对偏差(relative deviation, RD)如下：

(13)

式中：m为实际信号相关功率期望；m0为目标信号相关功率期望(即干扰信号对应的天线增益为0时的m).

图3给出的是实际接收信号相关功率的相对偏差曲线，二者均表现为有偏置的类余弦振荡. 偏置项均随着卫星高度角的增大而迅速减小，振荡频率与天线高度有关，振荡包络随着卫星高度角的增大先迅速衰减至零再增大并伴随一定波动，振荡相位于振荡包络过零位置发生翻转. 根据式(11)，振荡包络过零以及振荡相位翻转是信号反射附加相移造成的，过零翻转角(包络过零、相位翻转对应的卫星高度角)与天线增益和反射面介电常数有关.

图3 相关功率测量相对偏差Fig.3 Relative deviation of correlation power measurements

在本文仿真条件下，RHCP天线接收信号相关功率相对偏差波形过零翻转角为24.8°，LHCP天线接收信号相关功率相对偏差波形过零翻转角为8.3°. 对于RHCP天线接收信号相关功率：卫星高度角小于24.8°时相对偏差极大，其绝对值最高超过80%；卫星高度角大于24.8°时相对偏差保持较低水平，绝对值最高不超过7%. 对于LHCP天线接收信号相关功率：卫星高度角小于8.3°时相对偏差较大，其绝对值最高超过40%；卫星高度角大于8.3°时相对偏差仍保持较高水平，绝对值最高接近60%. 可见，RHCP天线方向性仅在低卫星高度角范围内对直射目标信号相关功率测量形成较大偏差，而LHCP天线方向性在整个卫星高度角变化范围均会对反射目标信号相关功率测量造成显著偏差.

3.2 随机误差分析

信号相关功率测量的随机误差表现为噪声引起的信号相关功率的随机变化. 由于实际信号与目标信号的相关功率具有不同的均值，故无法通过比较二者方差判断它们的离散程度. 为此，定义信号相关功率的离散系数(coefficient of variation, CV)

(14)

式中:σ为信号相关功率的标准差；m为信号相关功率的期望.

图4给出了实际信号与目标信号相关功率的离散系数仿真结果. 可见，天线方向性的不理想同样造成了实际信号相关功率离散系数曲线的周期波动，波动周期与天线高度相关，波形包络和相位也在与相对偏差波形相同的过零翻转角处完成过零和翻转.

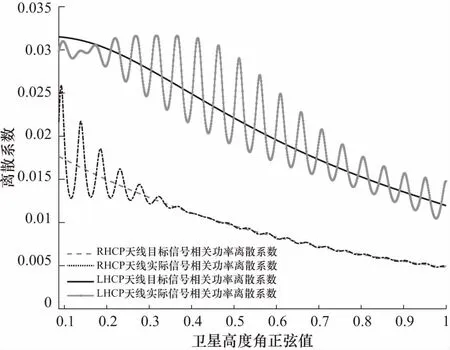
图4 相关功率测量离散系数Fig.4 Coefficient of variation of correlation power measurements

下面对在本文仿真条件下得到的相关功率离散系数进行分析. 对于RHCP天线接收信号相关功率离散系数：在卫星高度角低于24.8°时，其波动幅度随着卫星高度角的增大迅速减小，整体上与对应范围内的目标信号相关功率离散系数有显著差别；卫星高度角高于24.8°时，其波动幅度虽略有上升，但整体上几乎与该角度范围内的目标信号相关功率离散系数相同. 对于LHCP天线接收的信号相关功率离散系数：在卫星高度角低于8.3°时，其波动幅度也随着卫星高度角的增大而减小，但整体上与该范围内的目标信号相关功率离散系数差别较大；在卫星高度角高于8.3°时，其波动幅度随着卫星高度角的增大先增大再减小，整体上仍与目标信号相关功率离散系数保持显著差别. 如此可见，RHCP天线方向性的不理想主要造成了低卫星高度角范围内直射目标信号相关功率测量的随机误差变化，而LHCP天线方向性的不理想使得整个卫星高度角变化范围内的反射目标信号相关功率测量随机误差产生了显著变化.

4 结 论

地基GNSS-R功率测量应用中，天线方向性的不理想既会造成目标信号相关功率测量的系统误差，也会引起目标信号相关功率随机误差统计特性的变化. 在本文给出的仿真条件下，RHCP天线方向性仅对低卫星高度角范围内的直射目标信号相关功率测量有较大影响，而LHCP天线方向性在整个卫星高度角变化范围内均对反射目标信号相关功率测量有显著影响. 如何减弱甚至消除天线方向性带来的影响，需要在今后的研究中加以考虑.