集成填充的可重构杂凑算法电路设计与实现

陈韬， 连宜新， 李伟， 南龙梅

(战略支援部队信息工程大学 密码工程学院，河南，郑州 450001)

区块链技术作为新一代信息技术的代表，在金融、经济、科技等领域应用前景广泛，而杂凑算法用于完成区块各节点的数据正确性认证[1]. 区块链系统在设计上满足可以在无需硬分叉的条件下替换或更新密码算法，以满足应用场景、合规性、性能或者安全性的要求[2]. 此外在杂凑算法的设计方面，最具有代表性的就是SHA-3标准的设计，SHA-3具有优秀的设计、高效的软硬件实现效率以及灵活的适应性，标志着国际杂凑算法的设计达到了一个新的高度[3]. 二者共同对杂凑算法的可重构实现提出了新的要求，但目前针对杂凑算法的研究大都停留在单一算法或少数算法的硬件实现，在新的SHA3标准发布后缺少针对SHA3算法的支持[4-6].

在单一算法实现上，文献[7-8]采用多轮合一的方法分别对SM3、SHA1性能优化，但这种方法带来的是运算和填充资源的成倍增加；文献[7-9]都采用了调整运算缩短数据路径，有一定借鉴意义；文献[10]对SHA2系列算法单纯进行了实现，并加入了填充电路，在连续注入情况下，扩展电路能够和运算电路并行工作；文献[11-12]针对SHA3算法实现采用了流水线方式，对多消息处理性能提升明显，但流水线带来了数据相关和资源消耗问题，对于迭代类型的算法单消息处理性能没有提高，反而增大了面积开销和控制负担. 而在多个算法的重构上，文献[13]采用单纯加法器复用方式，文献[14-15]利用CSA对算法进行加速，但CSA的方式对运算不相似的算法优化力度大大降低，此外文献[13-15]都缺乏填充模块的设计. 文献[14-15]对数据扩展模块进行了优化，但实际上关键路径不可能在数据扩展模块上，优化的意义也不大，反而硬件填充方式相比较软件填充能够实现部分算法性能优化.

本文分析了算法涵盖的2类填充规则共6种分组位宽的情况，设计了支持所有算法的填充电路. 此外设计的运算电路在基于文献[13]运算单元基础上，采取寄存器复用方式将SHA3算法加入进来，最后实现了5类杂凑算法从输入、填充、扩展、运算到输出的完整电路.

1 算法分析

目前常见的杂凑算法有MD5、SHA1、SM3、SHA2系列和SHA3系列，虽然不同算法涉及到的运算结构不同，但是整体流程类似，包括消息填充、消息扩展(SHA3除外)、迭代压缩.

1.1 填充电路分析

消息填充是对消息按照填充规则附加额外的比特数. 本文涉及到两种填充方式，需要对不同的情况进行分析，SHA3系列算法用到填充方式是Pad10*1，记作方式1. 而其他算法填充规则类似，记作方式2.

1.1.1方式1

记待填充消息为M，填充后的比特流消息为P，首先在M后添加一个1，然后级联最小数量的0，最后添加一个1，使得填充后的消息比特长度|P|为分组长度x的整数倍.

填充过程可表示为：P←M||1||0d||1，其中的d为满足|M|+2+d≡0(modx)的最小整数.

其中||表示级联符号，0d表示有d个0，|M|表示消息M的长度值，x为1152/1088/832/768的一种取值.

1.1.2方式2

在消息后添加一个“1”，然后再添加若干个“0”，使得在没填充长度前现在的长度L满足：L≡(kmodM)，等式右边的值是固定值为64或者128，留出来这个值是因为长度信息是64或者128 bit.k为原始消息长度加上填充0,1 bit后的长度，M为分组长度值为512或1 024 bit.

整体上，由于总线宽度一般是32 bit，且各个消息分组正好是32的整数倍，故这里采用36×32 bit的寄存器组完成2类填充规则下6种长度的填充，而且可以想见该部分由于涉及到的情况较多，难点是在于控制路径的设计.

1.2 扩展电路分析

消息扩展是对填充后的消息分组进行逻辑变换得道算法对应轮数的数据字，这样能够保证每一轮都有对应的扩展数据参与运算，但是SHA3算法没有扩展算法，它的算法机理是填充后的数据直接进行计算. 填充扩展用到异或，移位，模加等操作.

将填充后的消息块按照算法处理字长分组：Xj=M0M1…M15,Xj为消息块，长度为512 bit 或者1 024 bit ，Mi为32 bit 或者64 bit . 最后的扩展算法如下：所有算法前16轮：Wi=Mi,0≤i<16,后面的扩展数据根据算法不同而不同，具体如下.

MD5：Wi=sel(M0～M15)，16≤i<64

SHA1：Wi=(Wi-3⊕Wi-8⊕Wi-14⊕Wi-16)<<<1，16≤i<80

SHA2：Wi=σ1(Wi-2)⊕Wi-7⊕0(Wi-15)⊕Wi-16)，16≤i<64(79)

SM3：Wi=P1(Wi-16⊕Wi-19⊕Wi-3<<<15⊕Wi-16<<<7)⊕Wi-6，16≤i<67

W’i=Wi⊕Wi-4，0≤i<64

其中函数P1为SM3算法规定的函数，σ1,σ0为SHA2算法规定的函数，函数sel表示MD5算法扩展后的消息字Ws根据轮数在16块消息字M0～M15中进行选择，W’i为SM3算法的第二类扩展数据，<<<表示循环左移，⊕为逐位异或运算.

考虑到为了让电路并行工作提高性能，即能够在多消息处理时下一分组的填充工作与上一分组的扩展及运算工作同时进行，并没有直接使用填充电路的寄存器进行复用，而是单独一套电路实现数据扩展. 另外如上文所说，由于扩展电路并不是最终的关键路径，因此没有优化的必要.

1.3 运算电路分析

各算法整体特征如表1所示.

表1 算法特征

根据对算法特征和上述算法过程的描述，并通过对上文算法过程的描述，可以确定运算电路是可重构的核心. 通过对本文涉及到的算法运算电路分析，MD5、SHA1、SM3、SHA2系列算法运算类似，最多用到8个64 bit寄存器，可以归为一类. SHA3算法由于运算机理不同，而且需要用到25个64 bit寄存器，这里单独处理.

表2为在用寄存器复用方法处理之后对每个寄存器赋值的介绍. 考虑到运算寄存器的复用，MD5、SHA1、SM3、SHA2系列4类算法可在前8个64 bit寄存器A～H实现各自运算电路，其中F_MD5，F_SHA1，F_SM3_L，F_SM3_R，F_SHA2_L，F_SHA2_R这些中间值是由寄存器经过一系列逻辑运算得来，具体的运算方式可分别参见文献[4].

表2 各算法运算赋值情况

SHA3算法较上面的算法运算较为复杂，表中无法清晰体现各寄存器的赋值，因此SHA3算法用伪码表示.

Round[b](A,RC)

θstep：C[x]=A[x,0]⊕A[x,1]⊕A[x,2]⊕

A[x,3]⊕A[x,4]

D[x]=C[x-1]⊕ROT(C[x+1,1])

A[x,y]=A[x,y]⊕D[x] 0≤x≤4,0≤y≤4

ρand π step：B[y,2x+3y]=ROT(A[x,y],r[x,y])

0≤x≤4,0≤y≤4

B[x+2,y]) 0≤x≤4,0≤y≤4

ιstep：A[0,0]=A[0,0]⊕RC 0≤x≤4,0≤y≤4

其中Round为SHA3轮函数，A为5×5×64的三维矩阵，由于操作位宽是64 bit ，可以直接略去第三维度z的表示.B，C，D为中间变量，ROT(A，r)表示64 bit的寄存器A[x,y]循环左移r位，r跟x，y有关的常量. ROT,Not分别表示循环移位和取反操作，RC是轮常数，r，RC具体取值见文献[5]. 文献[5]ρ step是循环移位操作，而π step是两个64 bit 寄存器的置换，因此两步可以合并成一步.

2 可重构硬件架构设计

在算法分析的基础上，利用硬件设计的一般思路，对杂凑算法的硬件电路划分成各个模块，最后通过顶层的信号连接实现在控制模块统一控制下，各个模块协调一致工作的功能.

2.1 整体设计框图

如图1所示，长度寄存电路存储128 bit 长度信息；模式存储电路存储5类算法的11个模式；报文填充扩展电路完成报文的注入、填充；扩展电路完成数据的扩展，与运算电路并行工作；运算电路完成算法的迭代压缩部分；IV存储和输出电路实现IV存储、更新，并输出最终的结果；控制器发出各模块使能、部分数选信号、全部的输出标志信号. 整体上在控制模块统一调度下，各模块按照报文注入、填充、数据扩展和运算共4个阶段工作，最终完成一个消息分组的处理. 设计核心是报文填充电路状态设计和运算电路设计，下面会着重说明.

图1 整体电路框图Fig.1 Circuit block diagram

2.2 报文填充电路

报文填充电路完成消息的注入、填充，以得到一个完整的消息分组. 如图2所示，报文填充电路最主要的功能就是对数据的选择，前期注入消息分组Data_in_reg，最后一组消息根据是否是32的整数倍而作适当变换为Data_in_reg⊕Length_decode，其中Length_decode根据最后一组数据有效位从1位到31位分为31种情况. 最后一组消息或者变换后的数据注入后，就进入关键的填充阶段. 填充数据根据最后一组32 bit 数据到来时计数器计数值和算法的不同而区分，数据的选择反映在电路里就是控制信号的不同，即控制状态的不同. 实际上由于杂凑算法运算电路只是简单的循环迭代，因此整体电路控制核心也在报文填充电路. 如图3和表3所示，报文填充的各个状态根据填充数据的不同而划分. 由于存在填充过程中消息分组长度已经达到算法运算的要求的情况，还需要在当前分组完运算后填充最后一个消息分组，图4和表4会说明这点，即状态机直接从S4_3跳转到填充不同填充数值对应的状态. 图3和图4的状态跳转条件可根据上文分析得到.

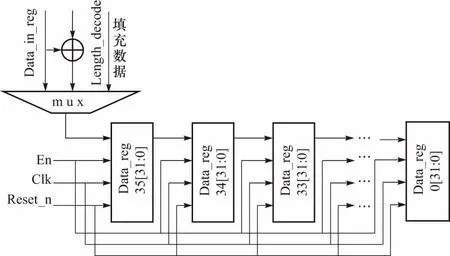
图2 填充电路Fig.2 Padding circuit

图3 填充状态示意图Fig.3 Padding in partial state transition diagram

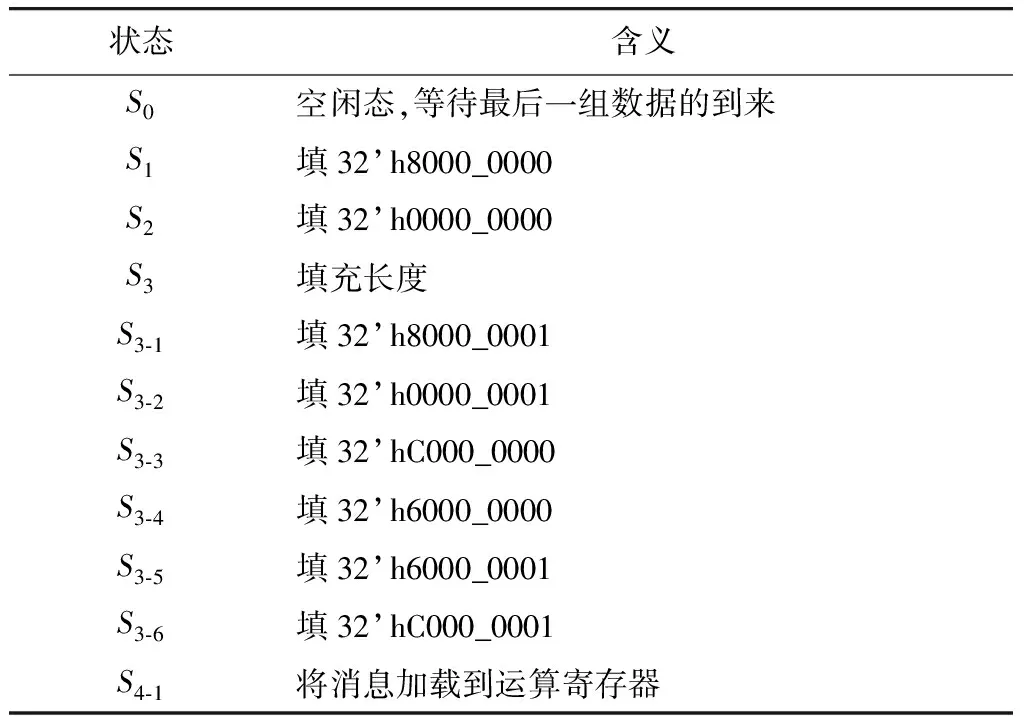
表3 状态含义

如图4所示，运算和输出部分转移图涉及到的各个状态含义如表4所示.

图4 运算和输出状态示意图Fig.4 Operation and output state diagram

表4 状态含义

2.3 报文运算电路

运算电路针对全体共5类算法的迭代压缩部分，是制约算法性能的关键. 由于结构的不同，对SHA3单独采取一套运算电路，而又由于运算的类似，对其余4种算法进行了逻辑资源复用，整体上采用了寄存器复用方式削减资源消耗. 由于共用运算寄存器Op_reg0～Op_reg24,而两类电路赋初值方式不同，因此在寄存器复用下整体的数据路径示意如图4所示，其中轮运算指的是运算电路1和2，1针对MD5、SHA1、SM3、SHA2系列算法，2单独针对SHA3系列算法，5类算法总共需要用到25×64 bit 的寄存器组，即所有的算法在这25个寄存器里完成迭代压缩，如图5所示.

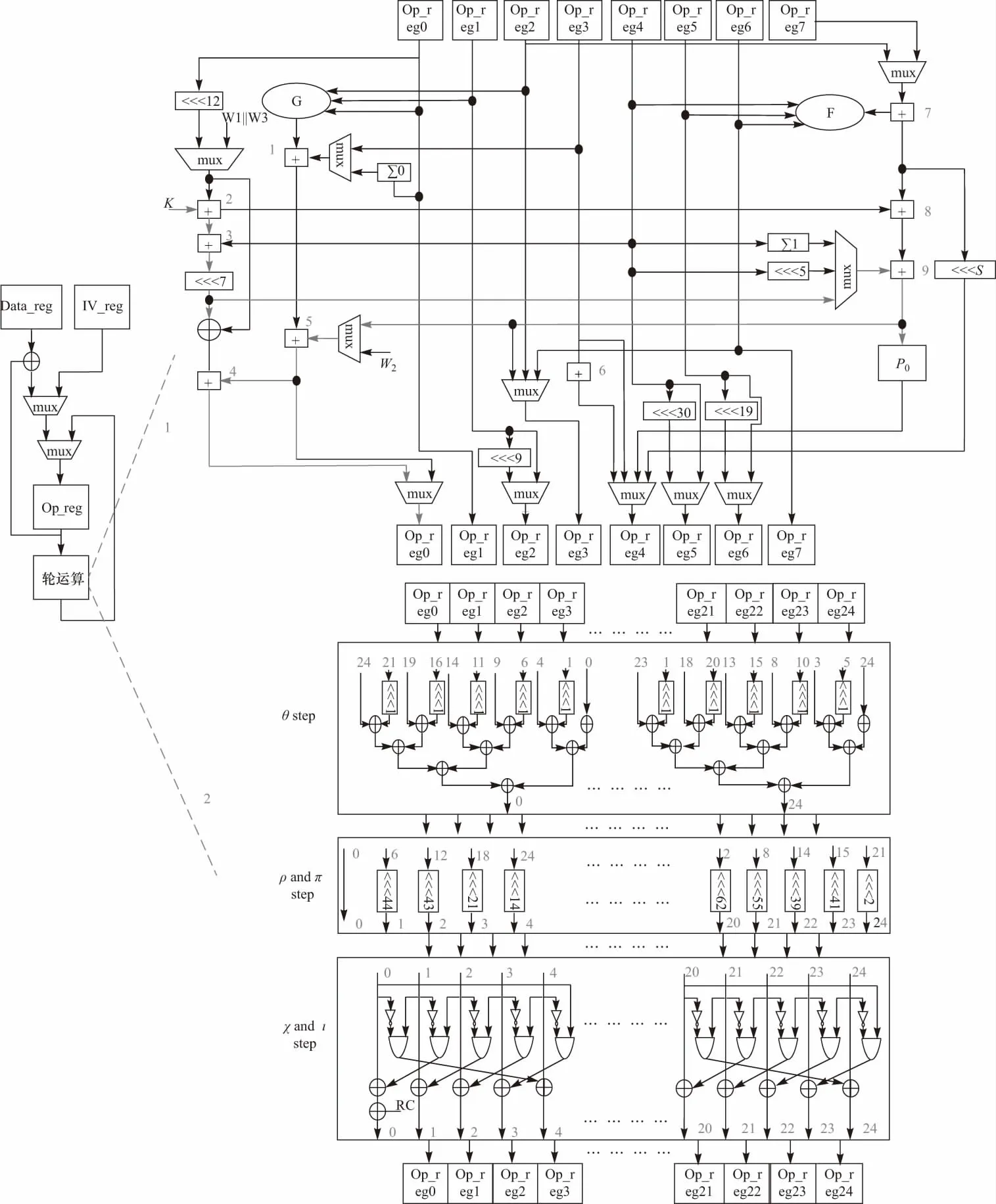
图5 运算电路Fig.5 Operation circuit

运算电路1用到8个寄存器Op_reg0～Op_reg7，后17个寄存器因为没有用到所以没有展示，内部加法器没有采用CSA加法器对数据路径进行加速，CSA是3进2出的加法器，无法对2个数据的和进行选择，因此选取普通加法器作为基础运算逻辑. 在节约运算资源方面采用加法器复用的方式[13]，对加法器按照有共同项的原则进行复用，因此共用到9个加法器，与文献[13]相比多1个加法器，本文并没有将4号加法器跟6号加法器合并，原因是两个加法器的输入缺少共同项，合并反而增大了关键路径延迟，因此与文献[13]略有不同，最终的关键路径为4个加法器和3个数选器延迟之和. 参数k通过寄存器存储后，根据计数器计数值选择参与运算的参数，因此关键路径起始寄存器落到了计数器而不是运算寄存器.

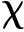
3 性能分析

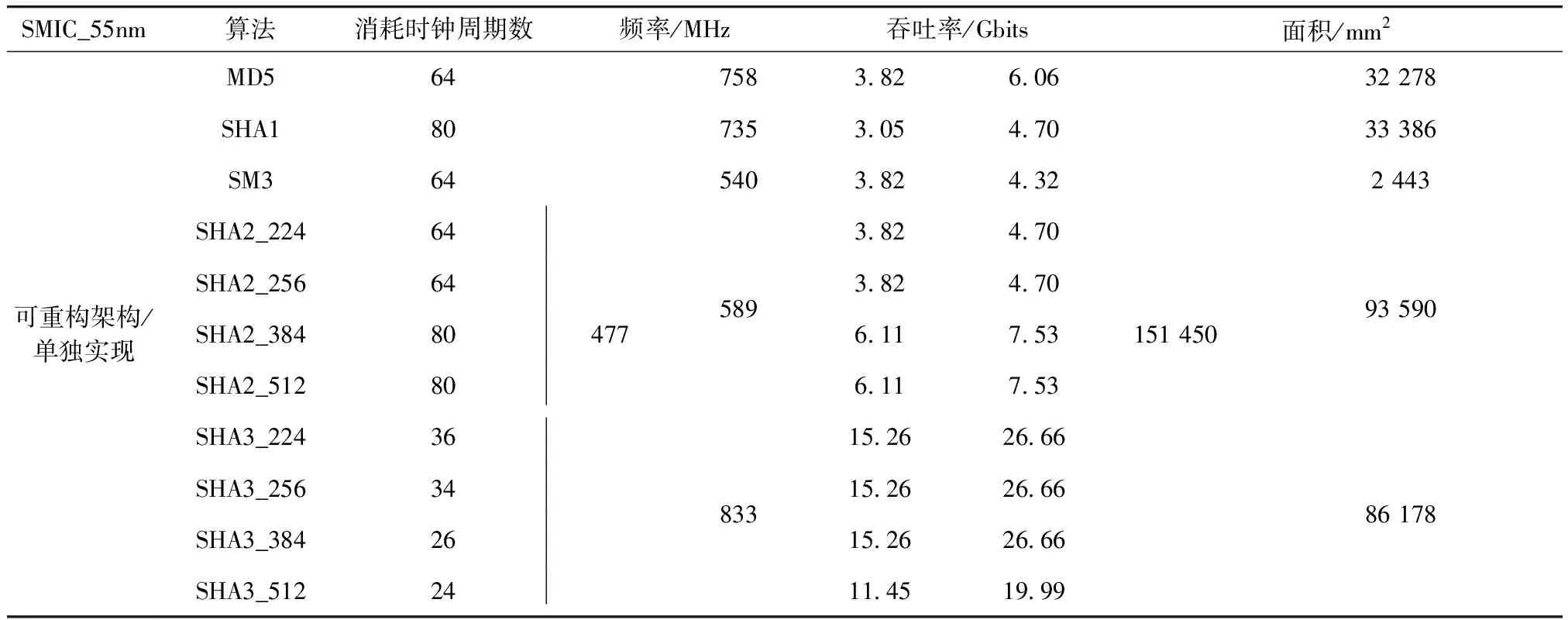
表5 性能指标

由表5可以看出，可重构算法电路在性能上相比较单算法有不同程度的降低，与MD5、SHA1、SHA3频率相差较大，而与SHA2、SM3频率较为接近，这是由于MD5、SHA1、SHA3运算相对简单，关键路径较短，而SHA2、SM3运算相对复杂. 关键路径较长造成. 但是可重构算法电路在资源消耗上相比较各个算法面积之和降低了45%，有效降低了资源的消耗[16-17].

由表6可以看到，本文在文献[13]方法基础上加入SHA3算法实现. 资源消耗方面，本文相比文献[13]增加了45%的ALUT数量和56%的Resigester的数量，这是由于加入了SHA3算法增加了额外的寄存器和运算单元开销造成的. 性能方面，本文由于做了填充电路，电路在实现一个完整的消息分组运算相比较软件实现填充方式即文献[13]有效减少了消耗的时钟周期数，在时钟频率基本不变的情况下SM3吞吐率增加11%，SHA2_384,SHA2_512吞吐率增加22%，实现了性能上的提升.

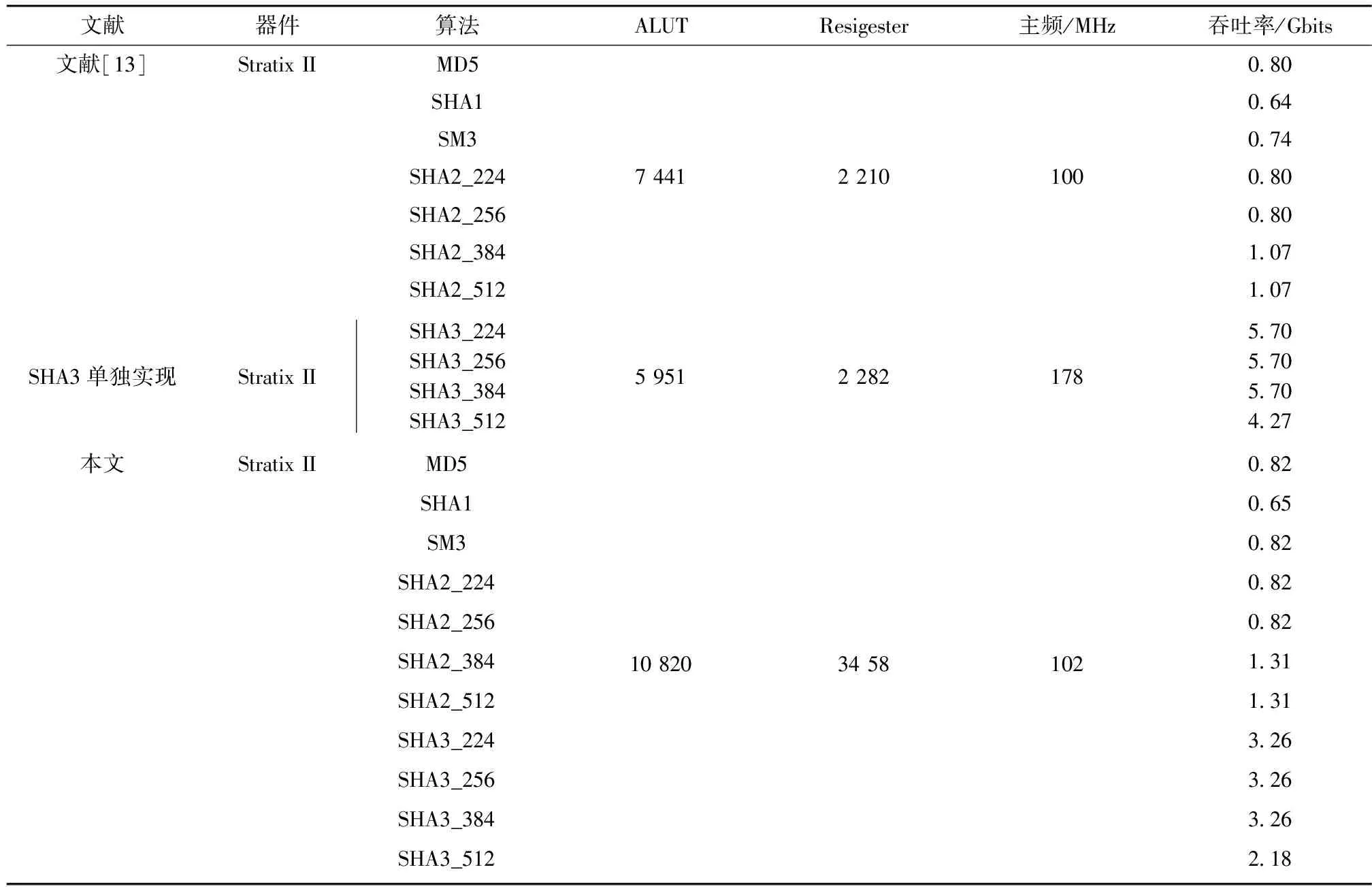
表6 性能对比

4 结束语

本文设计实现了可重构杂凑算法硬件IP，可直接挂载在总线上使用. 该IP特点是集成了文中所有杂凑算法的填充电路，并且在文献[13]的基础上修改了运算电路又加入了SHA3算法运算电路，在可重构能力方面，可单独灵活实现MD5、SHA1、SM3、SHA2系列和SHA3系列5类共11个算法. 最后实验得出各项性能指标，可重构电路相比较单算法实现资源消耗降低了45%，相比较之前的研究在SM3，SHA2_384,SHA2_512三个算法上吞吐率分别增加11%，22%，22%. 能够满足商用密码对于杂凑算法的需求，具有较高的实用价值.