商用车电液耦合转向系统主动回正控制研究*

耿国庆，李 浩，江浩斌，陈 杰，唐 斌

（1.江苏大学汽车与交通工程学院，镇江 212013；2.江苏罡阳转向系统有限公司，泰州 225318）

前言

转向系统是驾驶员与车辆交互的重要子系统，转向回正性能是评估车辆操稳性的一项重要指标。商用车仍普遍采用传统的液压助力转向系统（HPS）作为转向执行机构，但是HPS缺乏电子控制单元，无法对转向回正实施主动控制，严重影响车辆操纵稳定性与行驶安全性［1］。针对以上问题，国内外研究机构相继研发了多型电液耦合转向系统（electro⁃hydraulic coupling steering，EHCS）作为转向执行机构，相比于传统电控液压转向系统，EHCS可通过电动助力子系统直接调节转向助力矩和驾驶员转向路感，有效弥补了上述商用车主动控制的不足。目前，Volvo、ZF等公司均推出了电液耦合转向系统的相关产品［2］，使得EHCS及其控制技术成为提升商用车主动安全性能的重要部分。

国内外学者在车辆转向回正控制方面展开了大量的研究工作，高恪等［3］以转向盘转角和车速为控制信号，提出基于转角闭环的PID回正控制方法，提高了商用车转向回正控制稳定性；Kim等［4］考虑转向力矩和转向盘转角为控制信号，开发了EPS的控制逻辑，通过辅助电机的控制来提高转向盘的转向回正性能；Kurishige等［5］提出一种基于轮胎和路面产生的转向力矩估计的控制策略，能够优化转向盘的转向回正性能和保持良好的中心区转向路感。Chen等［6］根据车辆参数和转向摩擦的不确定性，设计回正滑模控制策略，提高了转向回正控制的稳定性和鲁棒性。以上研究对车辆主动回正控制技术的发展起到了积极的推动作用，但研究更多侧重于乘用车回正控制策略和算法的优化，而对于轴距较大且容易产生横摆和侧翻的商用车回正控制的研究较少。同时，对于如何获取算法中所涉及的车辆状态变量和路面附着系数等环境变量缺乏关注。

为了提高商用车转向回正工况下转向盘回正精度和车辆稳定性，本文中利用状态观测器实时估计算法中存在的车辆部分参数、路面附着系数等变量，采用滑模变结构控制算法设计车辆质心侧偏角与横摆角速度的联合控制系统，控制车辆质心侧偏角和横摆角速度无限逼近其期望值［7］。利用EHCS控制精度高、响应速度快的特点，实时叠加回正控制修正转角，解决商用车在回正过程中存在的低速回正不足导致的转向盘残余角过大，或高速回正过度导致的转向盘超调和振荡等问题。

1 动力学建模

1.1 整车动力学模型

车辆质心侧偏角的估算须计算轮胎力对车辆运动的影响，因此为了更好地表达车辆的非线性特性，选用了包括车辆纵向、侧向和横摆3个方向的运动和四轮回转运动的7自由度车辆模型［8-9］，如图1所示。

图1 车辆7自由度模型

车辆的运动方程如下。

纵向运动:

式中:vx为纵向车速；vy为侧向车速；ω为横摆角速度；a为质心到前轴的距离；b为质心到后轴的距离；m为整车质量；δ为转向轮转角；ay为侧向加速度；ax为纵向加速度；Iz为整车绕Z轴的转动惯量；Bf和Br分别为前后轴的轮距；ωij为车辆四轮角速度；Iw为车轮转动惯量；r为轮胎有效滚动半径；Tdij为车轮驱动转矩；Tbij为车轮的制动转矩。

1.2 Dugoff轮胎模型

为了准确计算轮胎处于不同路面附着系数的轮胎力和侧偏角，本文中选用Dugoff轮胎模型，该模型所需参数较少，有利于提高计算效率。轮胎的纵向力、侧向力可表示为

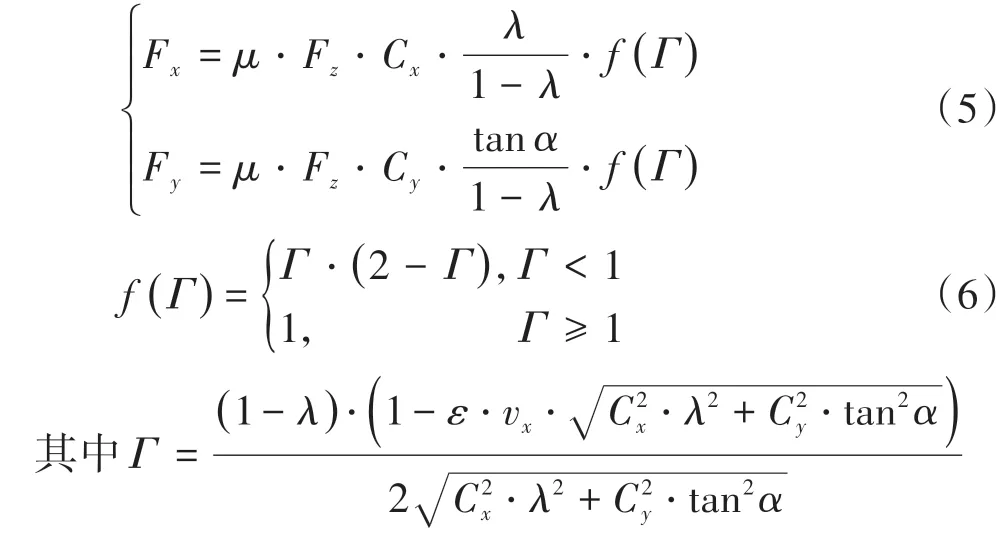
式中:Γ为边界值，用来表述轮胎的非线性特性；λ为纵向滑移率；α为轮胎侧偏角；Cy为轮胎侧偏刚度；Cx为轮胎纵向刚度；μ为路面附着系数；ε为速度影响因子，用于修正轮胎滑移速度对轮胎力的影响。

由于轮胎侧偏角α、轮胎垂向力Fz、滑移率λ和边界值Γ等参数与路面附着系数无关，因此Dugoff轮胎模型的数学表达式可以简化为以下归一化形式:

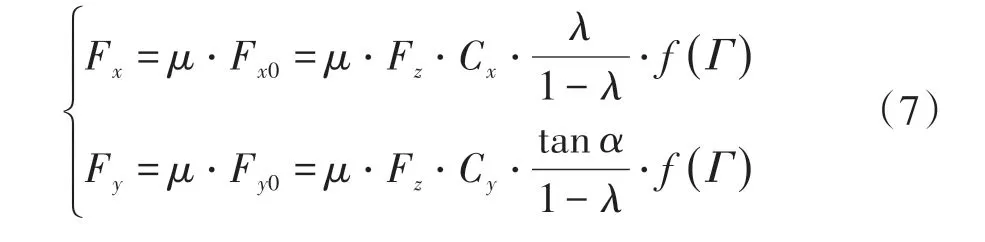
式中Fx0、Fy0为纵向侧向归一化轮胎力，与路面附着系数无关。这为UKF观测器估计路面附着系数提供极大的方便［10］。

车辆四轮垂向力的计算公式如下:

式中:hg为车辆质心高度；l为前后轴间距，l=a+b。

1.3 电液耦合转向系统模型

电液耦合转向系统的结构示意图和总成实物图如图2所示，EHCS系统主要由机械子系统、电动助力子系统、控制单元（ECU）和液压助力子系统组成。

图2 EHCS示意图

EHCS机械子系统包括转向盘-转向柱、转向螺杆-转向螺母、转向螺母-摇臂轴齿扇和摇臂轴齿扇-摇臂轴输出端等模型组成，各模型分别为

式中:Js1为转向盘-转向管柱等效转动惯量；Bs1为转向管柱转动黏性阻尼系数；Ks为扭杆刚度系数；θh为转向盘转角；θlg为转向螺杆转角；Th为驾驶员输入转矩；Jlg为转向螺杆等效转动惯量；Blg为转向螺杆黏性阻尼系数；Tc为转向轴操纵转矩；Ta为电机助力转矩；F为转向螺杆轴向工作载荷；llg为转向螺杆力中心距；mlm为转向螺母质量；xlm为转向螺母位移；Blm为助力缸阻尼系数；FH为液压系统提供的助力；Fs为传递到摇臂轴齿扇上的力；Js为齿扇等效转动惯量；θs为齿扇转角；Bs为齿扇黏性阻尼系数；rs为齿扇节圆半径；Tp为等效到摇臂轴上的转向阻力矩。

EHCS的电动助力子系统包括传感器、电动机和减速机构等。助力电机通过涡轮蜗杆机构将控制力矩耦合到转向管柱上。电机模型和减速机构如下:

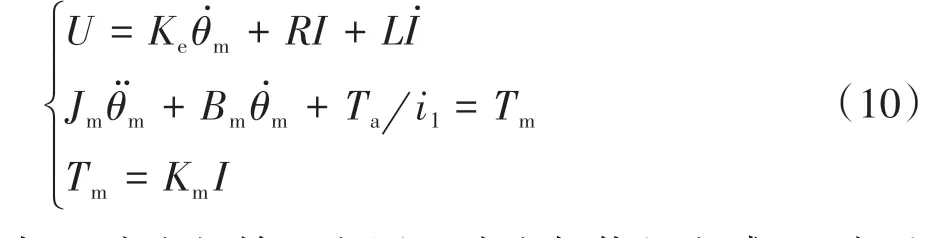
式中:U为电机输入电压；L为电枢绕组电感；Ke为反电动势常数；R为电枢电阻；I为电机电流；Km为电磁转矩系数；Jm为电机转动惯量；Bm为电机阻尼系数；Tm为电机额定转矩；i1为涡轮蜗杆传动比。

EHCS的液压助力子系统主要由转向泵、转阀和助力油缸组成。转阀开口面积A决定液压系统的助力大小，计算公式如下:

式中:Δθ=θh-θlg；W1为短切口宽度；W2为短切口宽度；L1短切口轴向长度；L2为预开间隙长度；Δθ为阀芯与阀套相对转角。

根据液压传动基本原理［11］，推导转向油泵和助力油缸的数学模型如下:

式中:Q为转向泵输出流量；np为转向泵输入转速；Vp为转向泵排量；QL为转阀进入液压缸的流量；Ap为活塞有效面积；xp为活塞位移；Ci为液压缸内泄漏系数；Δp为液压缸两端压差。

2 UKF观测器与车辆参数估计

2.1 非线性系统的设计

商用车主动回正控制需要获取车辆质心侧偏角、横摆角速度和路面附着系数等车辆和道路的状态参数，但是部分参数因测量成本过高或无法通过传感器直接测量等原因，利用传感器直接测量的方式难以在车辆中普及应用。本文中采用无迹卡尔曼滤波（UKF）算法构建系统状态方程和观测方程，利用车辆传感器获取横摆角速度、轮胎转角和车辆纵向及横向加速度等信息，实时估计控制算法中所需的状态信息［12-13］。

由式（1）～式（4）构建车辆的非线性系统:

式中:w(t)为过程噪声具有协方差阵Q；v(t)为测量噪声具有协方差阵R；取状态变量x=[β，ω，μfl，μfr，μrl，μrr]T；取观测量y=[ax，ay，ω]T；系统输入u=[δ]。

2.2 UKF状态观测器

考虑非线性系统的估计需求，研究人员提出利用UT无偏变换代替卡尔曼滤波中的非线性函数线性化的方法可得到无迹卡尔曼滤波（UKF）算法，UKF算法对非线性系统采用样本加权求和进而直接逼近随机分布，即用有限的变量来近似随机变量的概率统计特性从而代替传统线性化近似，体现了非线性近似算法更接近系统本质的思想［14］，无迹卡尔曼算法基本步骤如下。

（1）初始化设置

（2）迭代更新

选取第一组Sigma点集，根据对称采样策略生成2n+1个Sigma样本点集合:

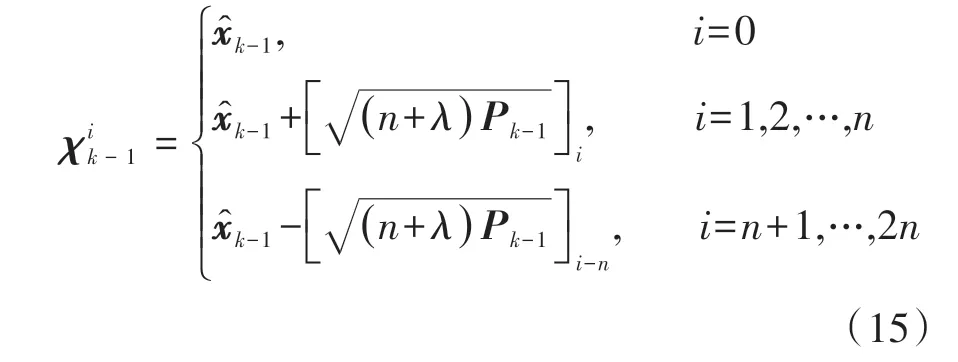
Sigma点相应的均值权值和协方差权值分别为

式中:n为待估计的状态向量维数；λ为比例参数；α为决定Sigma点分散度的尺度参数，取α=0.01；待选参数ρ为非负的权系数。

获取Sigma点集后，代入f(⋅)非线性系统方程计算预测样本点:

式中χi(k|k-1)是矩阵χ(k|k-1)的第i列，i=0，1，⋅⋅⋅，2n。

利用h(·)观测方程对变换后的Sigma点进行非线性转换，计算系统的预测观测量:

获得Sigma点集的预测值后，通过加权求和得到系统预测的均值与协方差:

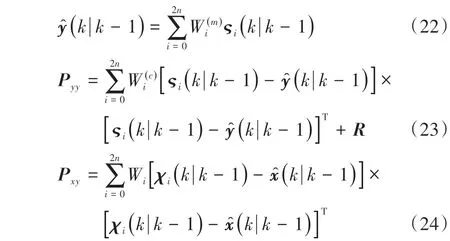
计算Kalman滤波增益矩阵:

UKF观测器的具体流程如图3所示，利用TruckSim搭建的汽车模型模拟输出的车辆实际转向盘转角、横摆角速度、侧向加速度和纵向加速度等作为轮胎模型及观测器的输入，根据式（14）～式（27）所示的算法、Dugoff轮胎模型和7自由度车辆模型，动态估计路面附着系数和质心侧偏角及其变化率等状态信息。

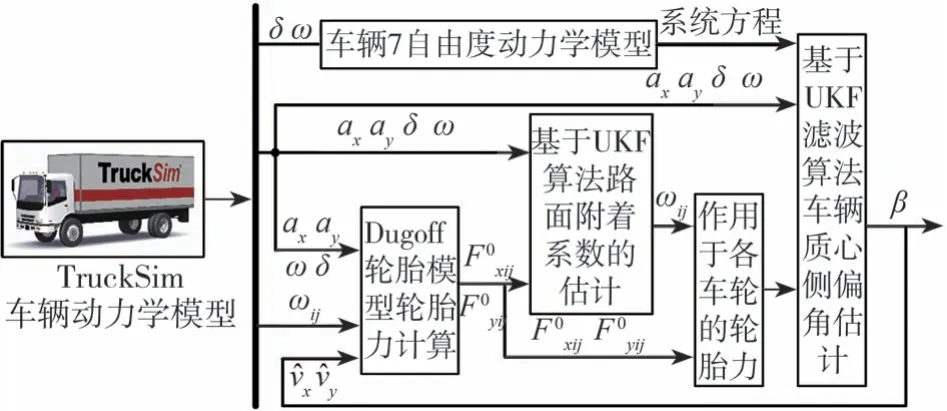
图3 路面附着系数和车辆质心侧偏角估计流程图

本文中利用TruckSim/Simulink联合仿真模型验证UKF观测器估计的路面附着系数和车辆质心侧偏角。路面附着系数估计的仿真工况设置如下:给定行驶工况为1 rad的转向盘转角阶跃输入，将TruckSim设置为商用车以80 km/h匀速行驶在高附着系数μ=0.85的路面和对开路面上（左侧路面附着系数为0.2，右侧路面附着系数为0.85），仿真结果如图4和图5所示。

图4 路面附着系数μ=0.85仿真结果

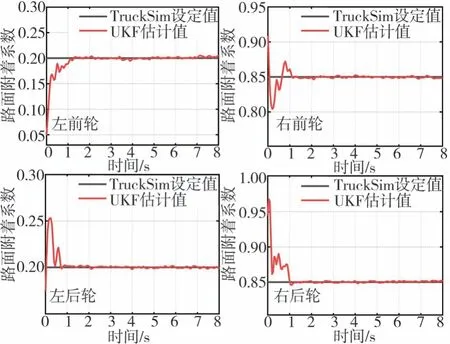
图5 对开路面附着系数仿真结果

质心侧偏角估计的仿真工况设置如下:本文采用TruckSim设置为双移线试验，模拟汽车避障和超车的工况，车速为80 km/h，μ=0.85，仿真结果如图6所示。

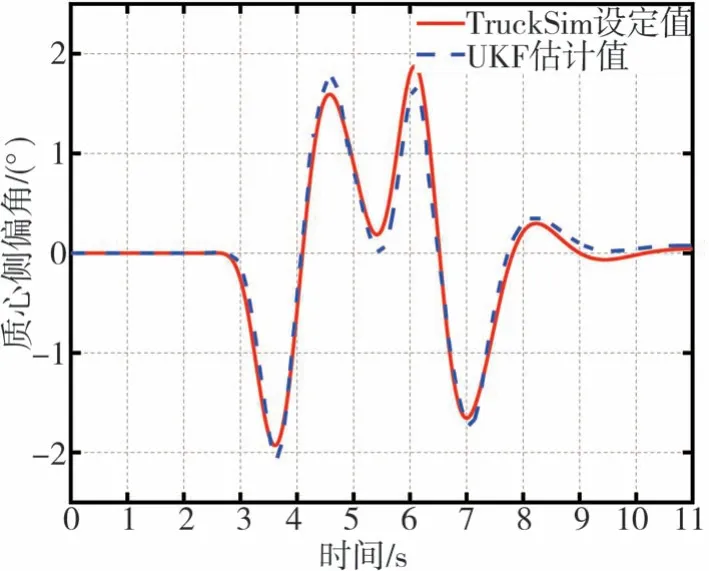
图6 双移线工况的仿真与估计值

通过图4～图6分析可知，UKF观测器可有效地对不同的路面附着系数进行实时估计，且估计误差较小，在可接受范围内。同时，观测器获取质心侧偏角的估计值与TruckSim输出的仿真值基本吻合，说明UKF观测器能够较为准确地估计汽车质心侧偏角，可为车辆转向回正控制提供准确的信息保障。

3 主动回正控制器的设计

本文中所提出的商用车主动回正控制结构图如图7所示，利用UKF观测器测量的车辆质心侧偏角、传感器获取的横摆角速度和7自由度模型输出二者的理想值作为控制器（联合滑模控制器）的输入，根据实际值与期望值的误差代入滑模面，在EHCS模块中计算滑模控制的转角修正量δ0，再与驾驶员施加的转向盘转角叠加，即为转向轮的总转角输入，使车辆横摆角速度和质心侧偏角无限趋近其期望值，从而达到车辆主动回正控制的目的。

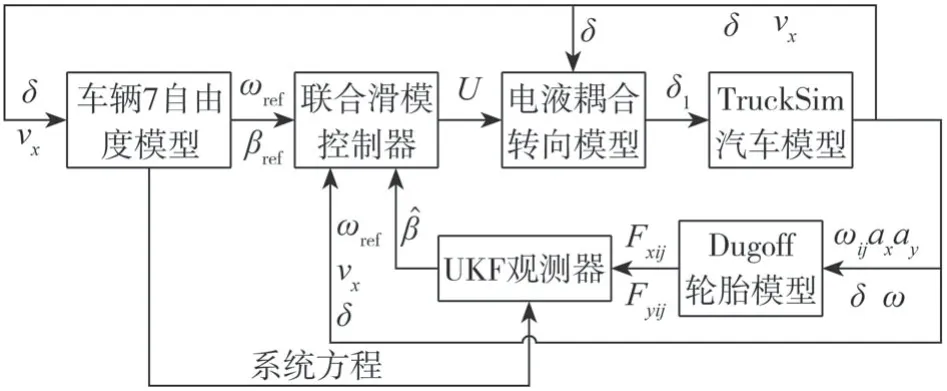
图7 主动回正控制结构图

3.1 横摆角速度和质心侧偏角的期望值

根据1.1节中建立的整车动力学模型，忽略纵向运动和车轮旋转运动可得汽车理想的2自由度模型:

因车辆期望的质心侧偏角和横摆角速度会受到路面附着系数的约束［15］，极限稳态下，车辆的横摆角速度限值设为ω=0.85μgvx，结合式（30）推导期望的横摆角速度:

质心侧偏角同样也会受到轮胎非线性和路面附着条件的限制，其限值β=arctan(0.02μg)，结合式（31）推导期望的质心侧偏角为

3.2 滑模控制器的设计

车辆的横摆角速度和质心侧偏角是表征回正控制稳定性的两个关键参数。但文献［16-17］表明，单独追求一个参数逼近其期望值往往会导致另一个参数的恶化。

本文中综合考虑商用车对横摆角速度和质心侧偏角的控制要求，为保证质心侧偏角在零位附近变化和车辆的横摆角速度跟随其期望值，提出了联合滑模控制算法，同时抑制车辆质心侧偏角和横摆角速度的变化。与单独控制质心侧偏角或横摆角速度相比，联合滑模控制具有更好的适用性和灵活性。滑模控制器的滑模面设计如下。

根据滑模控制理论，定义质心侧偏角控制滑模面:

设计横摆角速度控制滑模面［18］:

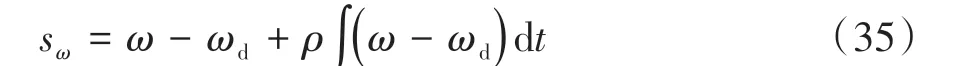
式中ρ为正的加权系数。

综合滑模面为

式中λ＞0为联合控制的权值系数，可根据实际工况需求加以调整，本文将λ取值为1。

对联合滑模面求导:

为了进一步抑制控制输入的高频振动问题，采用饱和函数sat(s)代替理想滑动模态中的符号函数sgn(s)［19］。

式（44）满足V̇=sṡ≤0，可知所设计的联合滑模控制系统渐进稳定。

4 仿真试验与结果分析

本文中通过TruckSim搭建了NMAY712商用车整车模型，为控制系统提供信号输入。根据设计的UKF观测器和滑模控制算法，对商用车回正工况进行仿真验证，EHCS系统模型与整车的部分参数如表1所示。

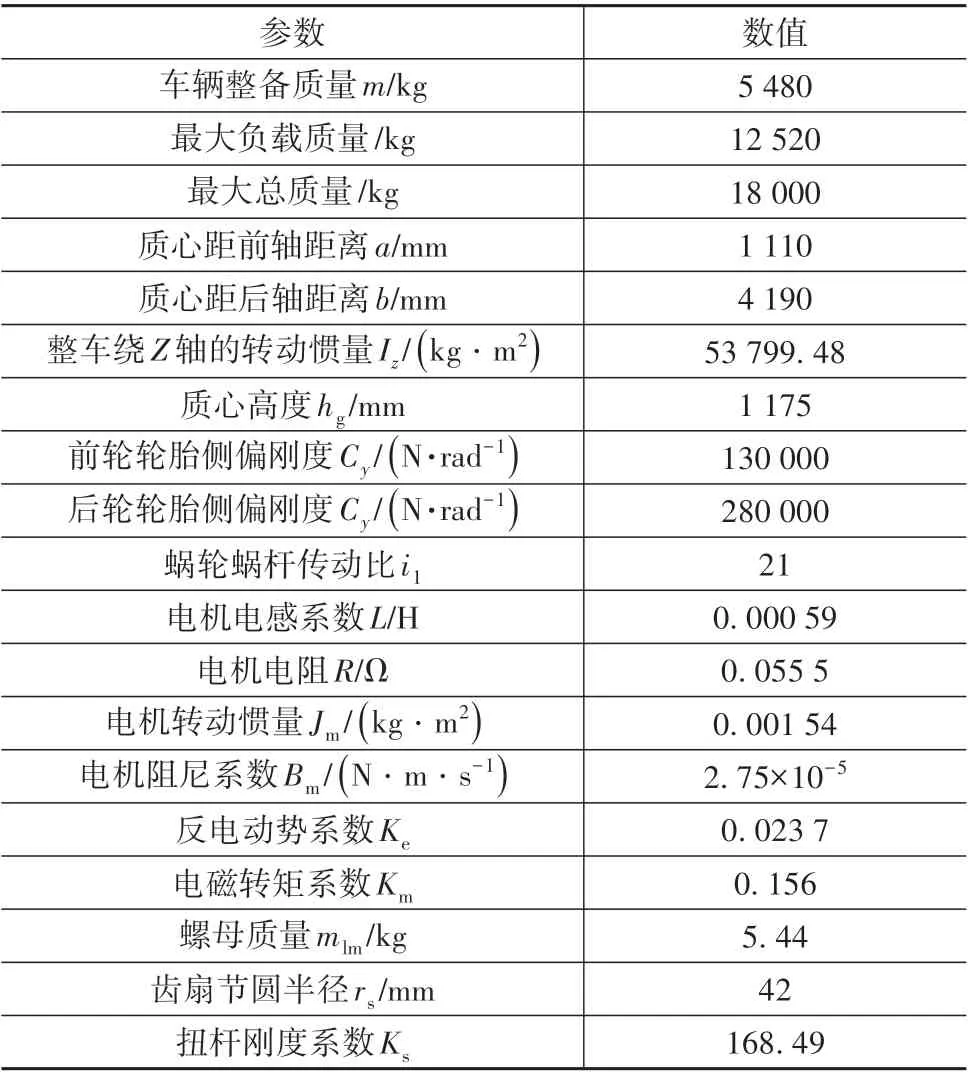
表1 EHCS模型与整车部分参数

4.1 滑模控制算法验证

为了验证联合滑模控制算法的有效性，在TruckSim中设置车辆双移线仿真工况和正弦仿真工况模型，结合EHCS转向系统和联合滑模控制算法Matlab/Simulink模型，对商用车转向稳定性控制进行综合测定。汽车双移线工况和正弦仿真工况的转向盘转角如图8所示。

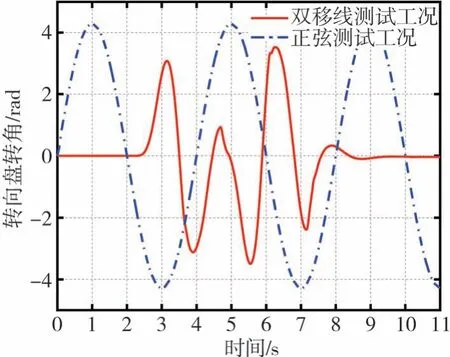
图8 转向盘转角输入

为了模拟商用车高速行驶时避障或超车的工况，采用双移线工况验证车辆操纵稳定性。设置车速80 km/h，路面附着系数μ=0.85，结果如图9所示，商用车转向轮在无控制条件下，转动速率快、转向幅度大。车辆高速行驶时，容易发生失稳或侧翻等危险工况。装配EHCS转向系统的商用车在联合滑模控制下，实时修正转向轮转角，优化了车辆高速超车或避障时转向轮的转动速率及转向幅度，避免了部分危险工况的发生，提高了车辆高速行驶安全性。

图9 双移线工况转向轮转角修正

双移线工况仿真结果如图10所示，对比无控制状态下，联合滑模控制系统对商用车转向系统的优化，大幅减少了车辆高速超车或避障时的横摆角速度与质心侧偏角的超调，使车辆的行驶轨迹更贴近其期望状态，改善了车辆的操纵稳定性。

图10 双移线工况仿真结果

为了验证控制系统的适用性与灵活性，在TruckSim中模拟车辆失稳状态，即在附着系数μ=0.2的路面上以80 km/h的车速，进行正弦输入工况的仿真验证，结果如图11所示。由图可知，无控制状态下，商用车的横摆角速度和质心侧偏角趋于发散状态，车辆已处于失稳状态。所设计的控制系统在车辆将要失稳时，通过EHCS转向系统快速、实时修正转向轮转角，使横摆角速度和质心侧偏角得到控制而接近其期望值。转向轮转角变化如图12所示。

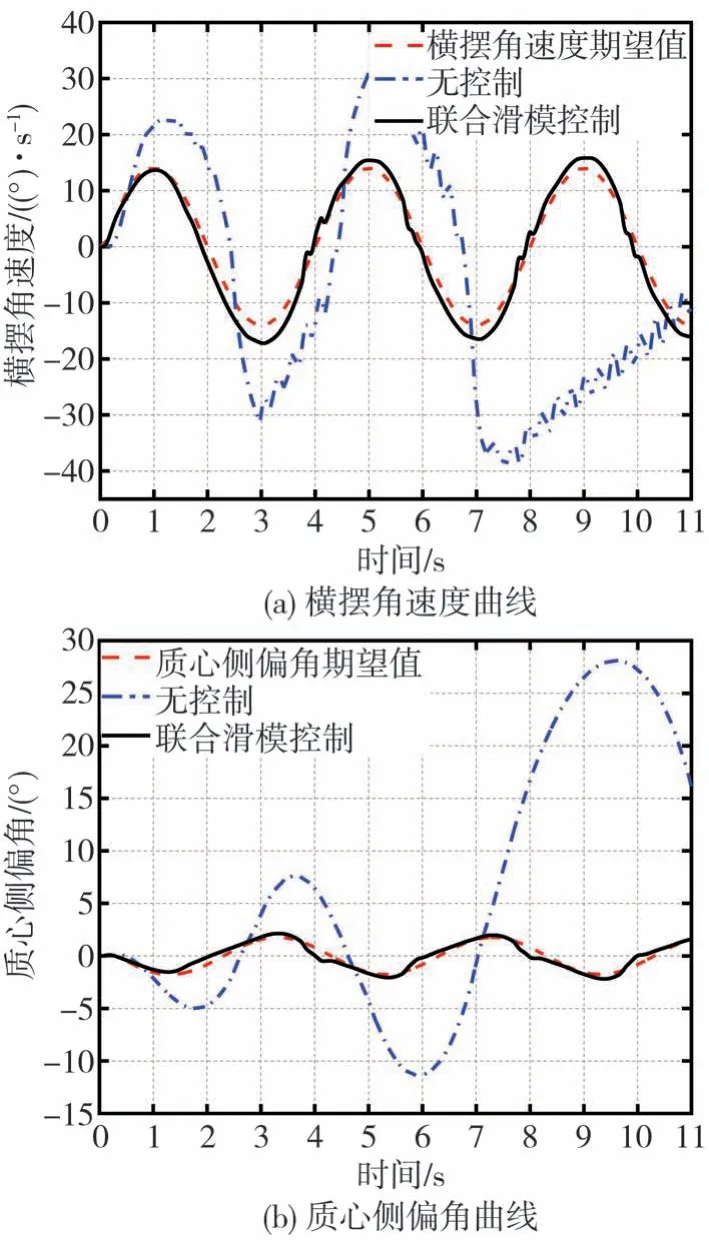
图11 正弦输入仿真工况

图12 正弦输入工况转向轮转角修正

综上所述，所设计的EHCS转向系统结合联合滑模控制算法有效地跟踪了车辆期望的横摆角速度和质心侧偏角，抑制了车辆失稳，避免了商用车高速避障或超车工况下危险状况的发生。

4.2 回正控制台架试验

为了验证所提出的转向回正控制算法，通过台架试验对商用车电液耦合转向系统的回正性能进行测试验证，如图13所示。转向器输入端连接伺服电机，模拟驾驶员转动转向盘，转向器输出端与负载液压缸相连，模拟转向阻力距。试验台架的硬件主要包括装有电动助力子系统的GYR01耦合动力电控转向器、电控转向系统控制器、转向台架WEIS⁃ZHXNT1、信号发生器、接收器和示波器等。

图13 电液耦合转向系统试验台架

选取典型车速20和80 km/h进行转向回正控制台架试验验证。转向盘输入端输入一个恒定力矩，当侧向加速度达到3 m/s2时，保持转向盘转角与车速稳定3 s，撤除转向盘力矩。对比回正过程在无控制、联合滑模控制、基于横摆角速度滑模控制或质心侧偏角滑模控制下［20］，转向盘转角的响应如图14和图15所示。

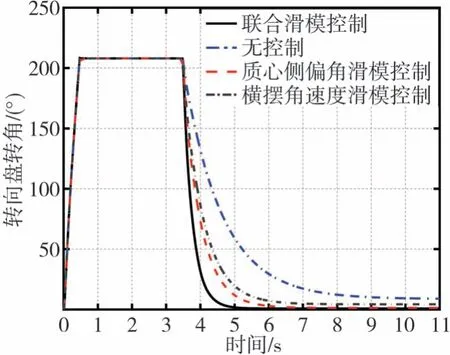
图14 低速回正试验转向盘转角响应

图15 高速回正试验转向盘转角响应

由图14可知，低速回正工况下，有回正控制的转向盘残余角比无回正控制明显减小，而联合滑模回正控制比单独控制质心侧偏角或横摆角速度有更小的残余角和更快的回正速度。

由图15可知，高速回正工况下，有回正控制的转向盘转角超调量，比无回正控制大幅减小，而联合滑模回正控制比单独质心侧偏角或横摆角速度的回正控制，对转向盘转角超调有着更好的约束效果与更快的稳定速度。具体数据对比如表2所示。

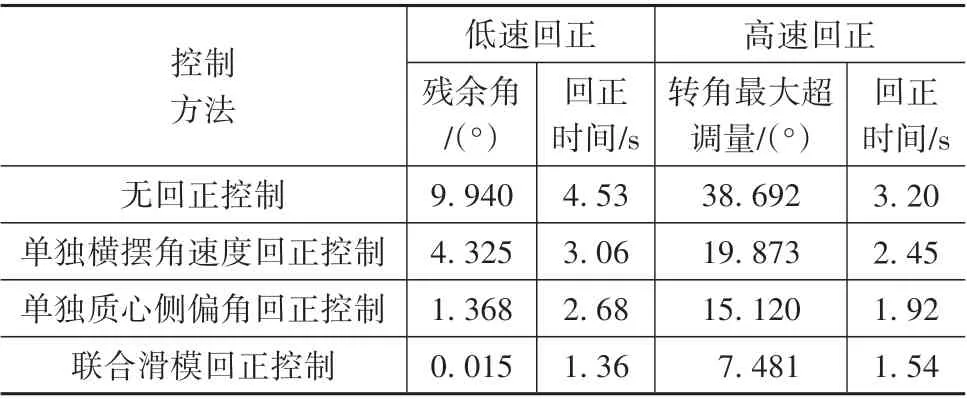
表2 台架试验结果分析

根据以上试验结果对比分析可知，与无控制单独质心侧偏角或横摆角速度回正控制相比，联合滑模控制的主动回正控制效果更为优越。

5 结论

（1）建立了7自由度非线性整车模型和Dugoff轮胎模型，针对控制算法中所需的车辆状态参数和路面附着系数难以直接测量的问题，本文中将纵向加速度、侧向加速度和横摆角速度等作为变量，搭建了UKF观测器模型，动态估计了路面附着系数和车辆部分参数，为回正控制系统的准确运行提供了稳定的信息；针对商用车回正过程中存在的低速回正不足或高速回正过度等问题，采用滑模变结构控制算法设计车辆质心侧偏角与横摆角速度的联合控制器，提高了车辆回正的稳定性和准确性。

（2）为了验证UKF观测器的准确性和联合滑模控制的有效性，利用TruckSim与Matlab/Simulink联合仿真，搭建转向试验台架，对观测器与控制算法进行试验验证，仿真与试验结果表明，UKF观测器能够较为准确估计车辆质心侧偏角和路面附着系数，联合滑模控制算法比无控制和单独质心侧偏角或横摆角速度控制有着更佳的主动回正控制效果。