基于GWO⁃KRG近似模型的乘员约束系统可靠性优化设计*

谷先广，高梦琳，王笑乐，黄岳竹

（1.合肥工业大学汽车与交通工程学院，合肥 230009；2.合肥工业大学智能制造技术研究院，合肥 230009；3.太航常青汽车安全系统（苏州）股份有限公司，苏州 215100）

前言

据世界卫生组织《2018年全球道路安全现状报告》统计［1］，全球的道路交通死亡人数仍居高不下，每年约有135万人死于道路交通事故。目前，道路交通伤害是全球所有年龄段人群的第八大死因，是5-29岁儿童和年轻人的主要死因。当碰撞发生时，乘员约束系统作为汽车安全系统的重要组成部分，可以有效限制乘员位移，减轻乘员损伤［2］。因此，在汽车安全性设计中，有必要对乘员约束系统进行优化设计，通过提升约束系统的防护性能来进一步降低乘员损伤风险。

在约束系统优化过程中，传统的确定性优化设计方法未考虑设计变量或参数的不确定性，由于乘员约束系统的复杂性和高度非线性，在实际工程应用中，确定性优化设计得到的最优解可能会不满足约束条件，而可靠性优化设计方法可以弥补确定性优化设计的不足，使优化解远离失效边界，提高设计方案可靠度［3-4］。因此，在确定性优化设计基础上开展可靠性优化设计具有重要的工程意义。

目前，乘员约束系统的优化方法主要是仿真模型与优化算法相结合，然而优化过程中直接调用仿真模型进行计算，效率低下。通过构建近似模型来代替仿真模型，可以提高优化效率，相比传统的响应面（response surface model，RSM）和径向基函数（radical basis function，RBF）近似模型，克里金（Kriging，KRG）近似模型不仅可以描述高度非线性过程，同时也能去除数值噪声和光滑目标响应，现已普遍应用于乘员约束系统优化设计中［5-6］。然而，单纯采用KRG模型需要大量样本点来构建，往往预测精度不能满足要求，文献［7］和文 献［8］中 将 粒 子 群 优 化（particle swarm optimization，PSO）算法应用到KRG建模过程，使用PSO算法得到KRG模型相关性参数的最优解，用最优解构建预测模型。然而，PSO算法收敛精度低，易陷入局部最优解［9］。

灰狼优化（grey wolf optimizer，GWO）算法［10］已被证明在收敛速度和求解精度上均优于PSO算法［11］，且全局寻优能力强。因此本文中提出采用GWO算法获取使KRG模型达到最佳预测精度的相关参数，用最优解构建高精度的近似模型并应用于后续的约束系统优化设计中。在GWO⁃KRG近似模型基础上，选取灵敏度高的约束系统参数作为设计变量，以加权损伤准则WIC作为优化目标，采用多岛遗传算法（multi⁃island genetic algorithm，MIGA）对约束系统进行确定性优化和可靠性优化设计，并利用蒙特卡罗描述抽样方法进行可靠性概率评估，最终得到既满足安全性能要求又满足可靠性需求的优化设计结果。

1 可靠性优化设计方法

确定性优化设计问题数学表达式如下:

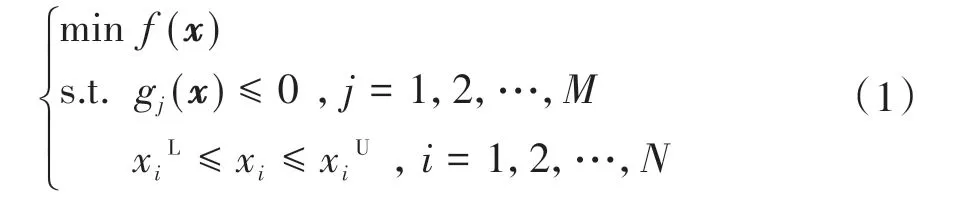
式中:f（x）为目标函数；gj（x）为约束函数；M、N分别为约束函数和设计变量个数；xiL和xiU分别为设计变量xi的下限和上限。

参数波动或其他外界因素的影响都可能导致设计结果与实际结果之间差距较大，引起潜在的性能损失和波动，甚至导致设计结果不可行。

因此，需对确定性优化设计的结果进行可靠性评估，判断确定性优化设计结果是否满足可靠度要求，若不满足工程要求，则需要在确定性优化设计基础上进行下一步的可靠性优化设计。可靠性优化设计既能控制失效概率在一个合适的水平，又能获得问题的优化解，表达式为

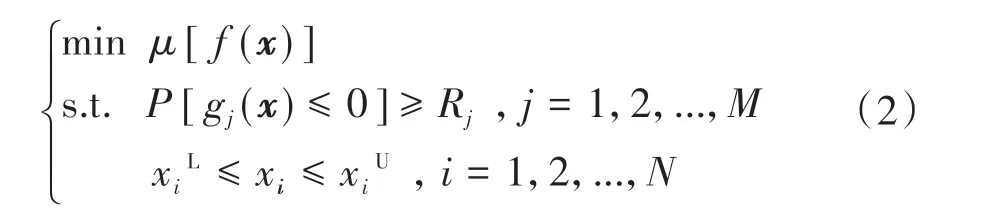
式中:μ为目标函数的均值；P［gj（x）≤0］为满足第j个约束函数的概率；Rj为约束函数gj（x）的期望可靠度。

失效概率的表达式为

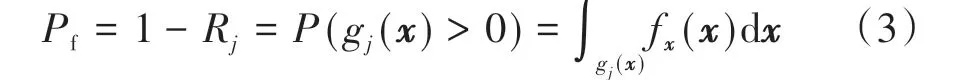
式中:Pf为失效概率；gj(x)＞0代表失效状态；f x(x)为基本随机变量的联合概率密度函数。

可靠性概率的计算方法主要有1阶可靠性方法、2阶可靠性方法和蒙特卡罗描述抽样方法。本文中采用蒙特卡罗描述抽样方法，先对基本随机变量进行大量采样，再对采样结果进行统计获得系统的可靠度。

2 GWO⁃KRG近似模型

2.1 GWO算法

GWO算法是一种群体智能优化算法，模拟了灰狼在自然界的捕食行为。GWO算法将狼群按适应度排序分为4组:α、β、δ和ω。优化过程如下所述。

（1）包围，灰狼与猎物间距离更新公式为

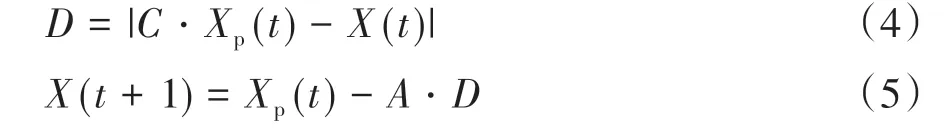
式中:D为灰狼与猎物之间的距离；Xp为猎物位置；X为灰狼位置；t为当前迭代次数；A与C分别为收敛系数和摇摆系数。

（2）追捕，ω狼在α、β、δ狼带领下不断更新位置:

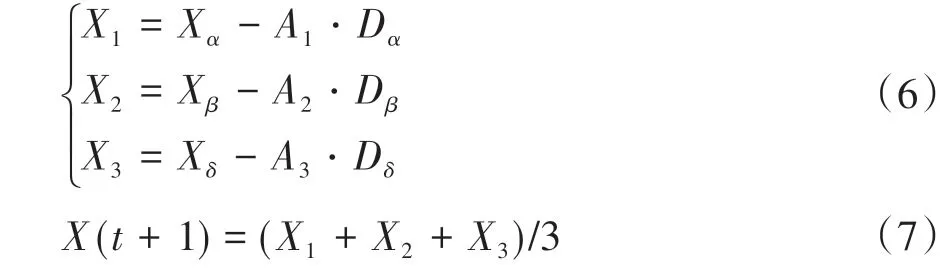
式中:Xα、Xβ、Xδ分别为α、β和δ狼的当前位置；Dα、Dβ、Dδ分别表示α、β、δ狼与ω狼之间的距离；X（t+1）为更新后灰狼的位置。

（3）攻击，狼群捕获猎物即为获得最优解，当|A|＜1灰狼进行局部搜索，当|A|＞1进行全局搜索。

2.2 KRG近似模型

KRG近似模型在拟合高度非线性问题时，容易获得理想效果，其由回归函数和随机过程组成，其预测形式为

式中:qT(x)为回归基函数；η为回归系数；z（x）表示均值为0、方差为σ2的随机过程。z（x）的协方差可以描述设计空间中任意两点间的相关性，表达如下:

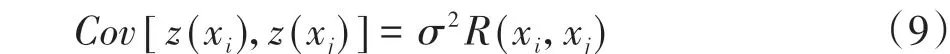
式中R（xi，xj）为任意两个输入变量间的相关函数，其选择是构建KRG近似模型的关键，采用工程上应用最广泛的高斯相关函数，表达形式为

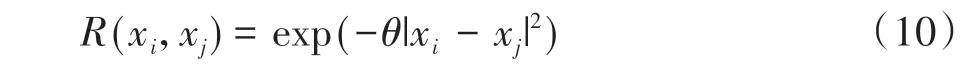
式中θ为相关性参数，描述函数输出对输入变化的敏感程度，因为σ2和β均为相关性参数的函数，那么KRG近似模型中唯一未知数即为相关参数，只要确定相关参数后，即可构建KRG近似模型。

2.3 GWO⁃KRG近似模型

只要确定相关性参数，便可构建KRG近似模型，故本文中使用GWO算法对其进行优化，优化过程即为寻找满足KRG近似模型最佳精度评价指标的相关参数值。本文中采用的近似模型精度评价指标为最大相对误差MRE和确定性系数R2，当MRE越接近0且R2越接近1时，所建立的近似模型精度越高。MRE和R2的表达式分别为

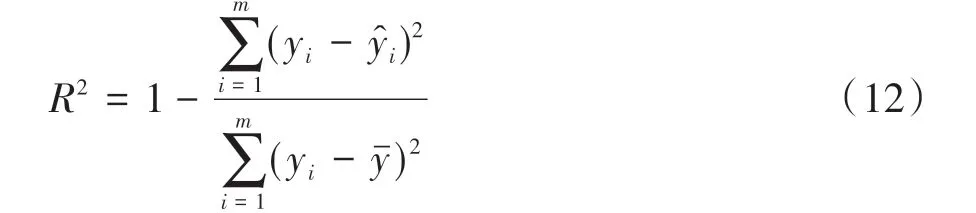
式中:m为验证点数目；yi、ŷi和yˉ分别对应验证点的真实响应值、近似模型预测响应值和所有真实响应值的平均值。

GWO⁃KRG近似模型的具体建立过程如下。

（1）确定设计变量及取值范围、优化目标和约束，设计变量为相关参数，范围为0.1-20，R2和MRE分别为优化目标和约束。优化表达式为

（2）使用试验设计方法在样本空间中获得样本点和验证点，样本点用来构建近似模型，验证点用来检验近似模型精度。

（3）设置狼群初始规模、最大迭代次数、优化参数维度及初始化α、β和δ狼的位置。

（4）应用GWO算法在整个可行域内搜索，不断更新α、β、δ狼和猎物的位置，直到满足最大迭代次数停止迭代；或满足终止条件，则认为算法收敛。

（5）用优化获得的相关参数建立GWO⁃KRG近似模型，若R2和MRE满足精度要求，则对相关参数进行统计，若不满足，则返回步骤（2）增加样本点。

（6）针对不同损伤指标，依次进行上述步骤（1）～（5）。

3 乘员约束系统可靠性优化设计

约束系统可靠性优化设计流程如图1所示。

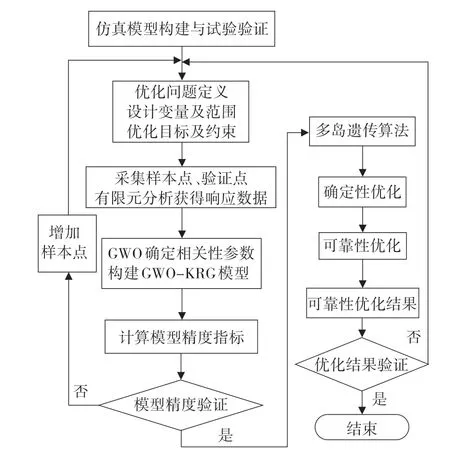
图1 可靠性优化设计流程图

3.1 模型建立与验证

基于某乘用车驾驶员侧尺寸布置，建立乘员约束系统数值模型。该模型主要由地板、座椅、转向系统、仪表板、防火墙、安全带、安全气囊和假人模型组成，如图2所示。

图2 乘员约束系统模型

为保证所建立的仿真模型能用于后续乘员约束系统的优化设计，须将仿真结果和实车碰撞试验结果进行对标。基于C⁃NCAP评价体系，在驾驶室内放置混Ⅲ型第50百分位假人，对该车进行初速度为50 km/h的正面100%重叠刚性壁障实车碰撞试验，并将B柱下端传感器测得的减速度曲线输入到仿真模型中。

试验获得的假人各部位伤害响应曲线、安全带力曲线与仿真计算得到的曲线对比见图3。典型损伤指标对比如表1所示。可以看出，仿真曲线与试验结果基本吻合，且各损伤指标的相对误差均在10%以内。综上所述，所建立的仿真模型满足精度要求，可用于后续优化设计。

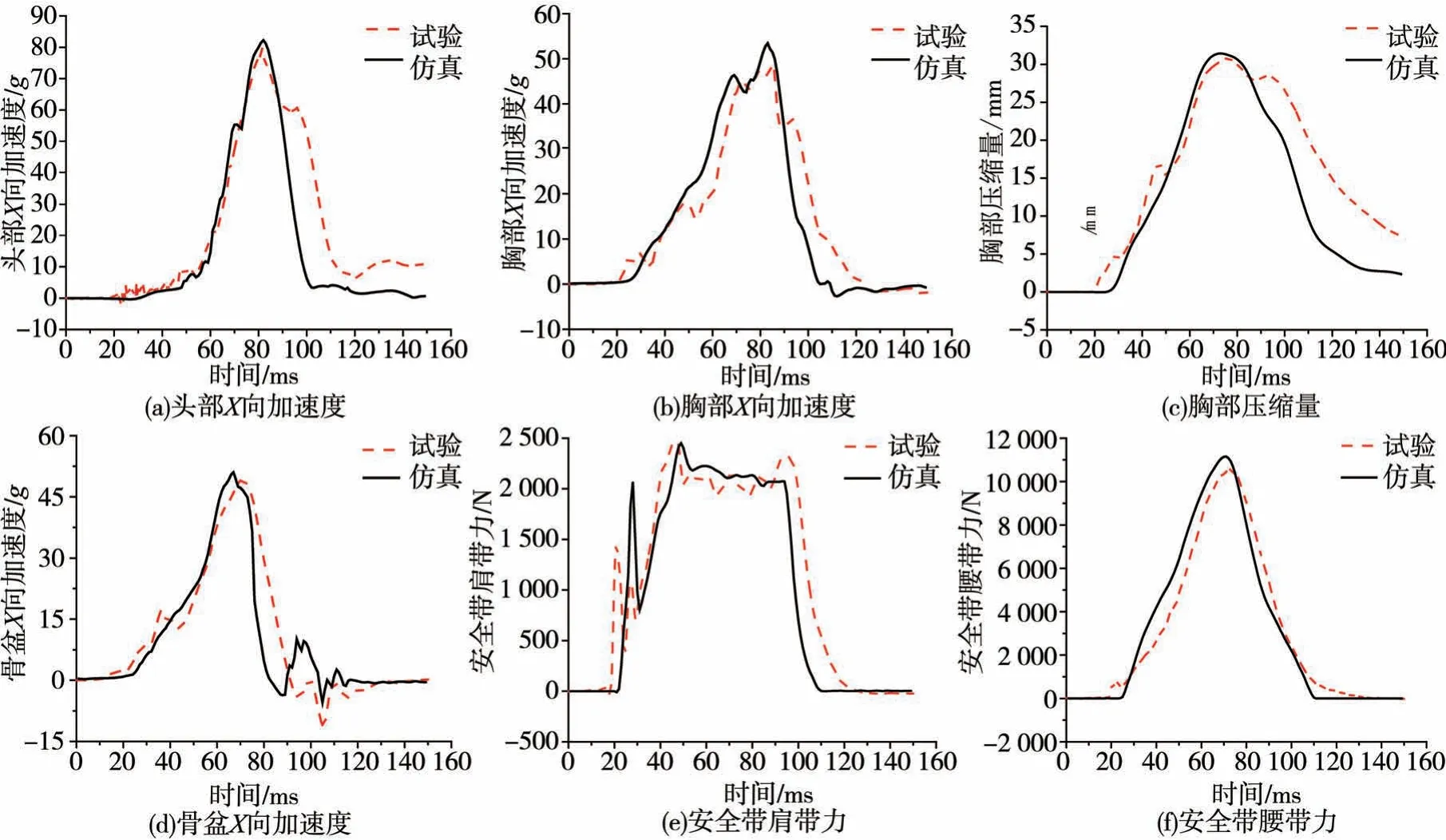
图3 仿真与试验的响应曲线对比

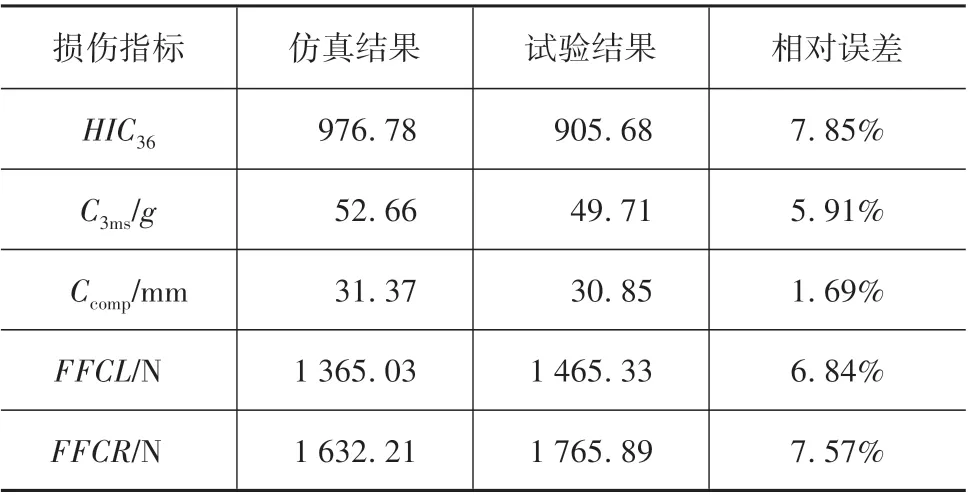
表1 损伤指标仿真与试验结果对比

3.2 优化问题定义

约束系统的设计参数众多，若同时进行优化设计效率极低，基于文献［12］中全局灵敏度分析的结果，选择包括限力器限力等级x1、预紧器预紧时间x2、排气孔直径x3、充气质量流率比例x4和气囊体积x5在内的5个参数作为后续优化设计的设计变量，考虑到加工精度和装配误差的不确定性，假设设计变量服从协方差系数为0.05的正态分布。各参数初始值与取值范围如表2所示。

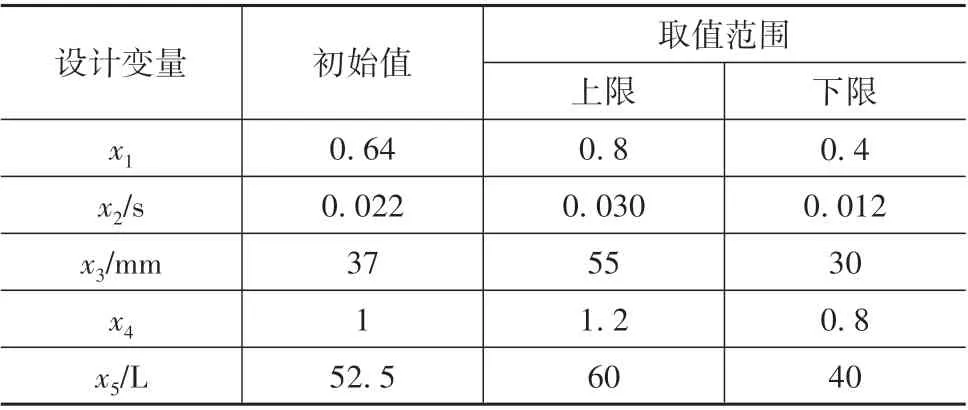
表2 设计变量初始值与取值范围

为综合并准确评价乘员损伤情况，以兼顾头、胸、腿部的加权损伤准则WIC［13］作为约束系统的优化目标，其表达式为

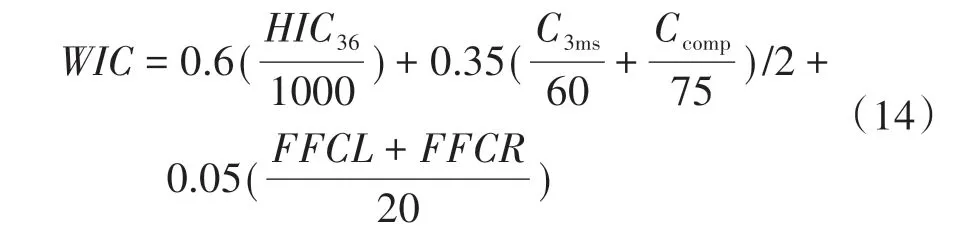
以头部伤害准则HIC36、胸部3 ms合成加速度C3ms、胸部压缩量Ccomp和左右大腿轴向力FFCL与FFCR作为约束，对乘员约束系统进行优化。参考GB 11551和C⁃NCAP中的评价标准，各约束条件初始值和优化目标值如表3所示。

表3 损伤指标初始值和目标值

3.3 试验设计

最优拉丁超立方试验设计（optimal Latin hypercube design，OLHD）方法可以在设计空间中生成更为均匀的样本点，因此，使用OLHD方法在设计空间中分别采集50组样本点和15组验证点，提交MADYMO进行仿真计算，得到每组数据对应的损伤指标值。

3.4 GWO⁃KRG近似模型的建立

在建立GWO⁃KRG近似模型过程中，需对GWO算法的初始参数进行设置，经过多次调试，最终确定的GWO算法参数设置为:种群数量为100，最大迭代次数为1 000，优化参数维度为5。

针对每个损伤指标，应用GWO算法对KRG近似模型的相关参数进行优化，终止条件为GWO算法满足连续200次迭代，且每次迭代误差不超过1×10-12。表4为GWO算法最终确定的最优相关参数。

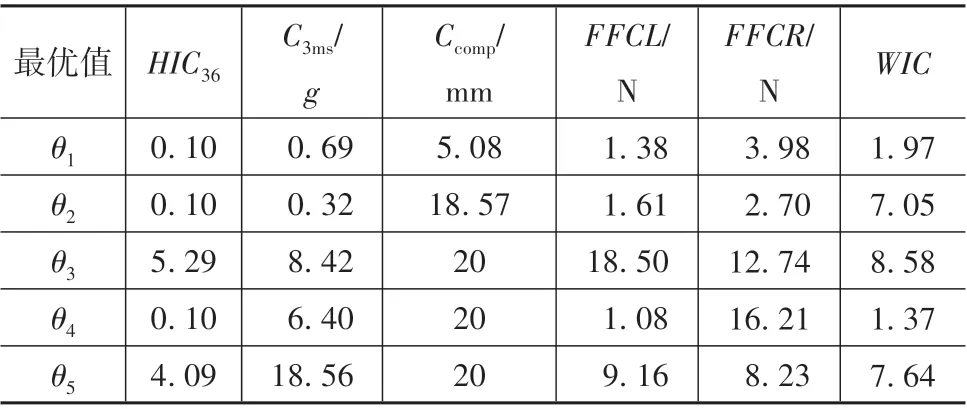
表4 GWO⁃KRG近似模型最优相关参数

为验证GWO⁃KRG近似模型的预测优势，基于采集的样本点，首先构建了RSM、RBF和KRG 3种传统近似模型，随后构建了PSO⁃KRG模型，并将以上4种近似模型与GWO⁃KRG近似模型进行对比。为保证公平，PSO初始参数的设置同GWO算法。PSO⁃KRG和GWO⁃KRG的精度用15组验证点来检验，所有近似模型的精度对比结果如表5所示。

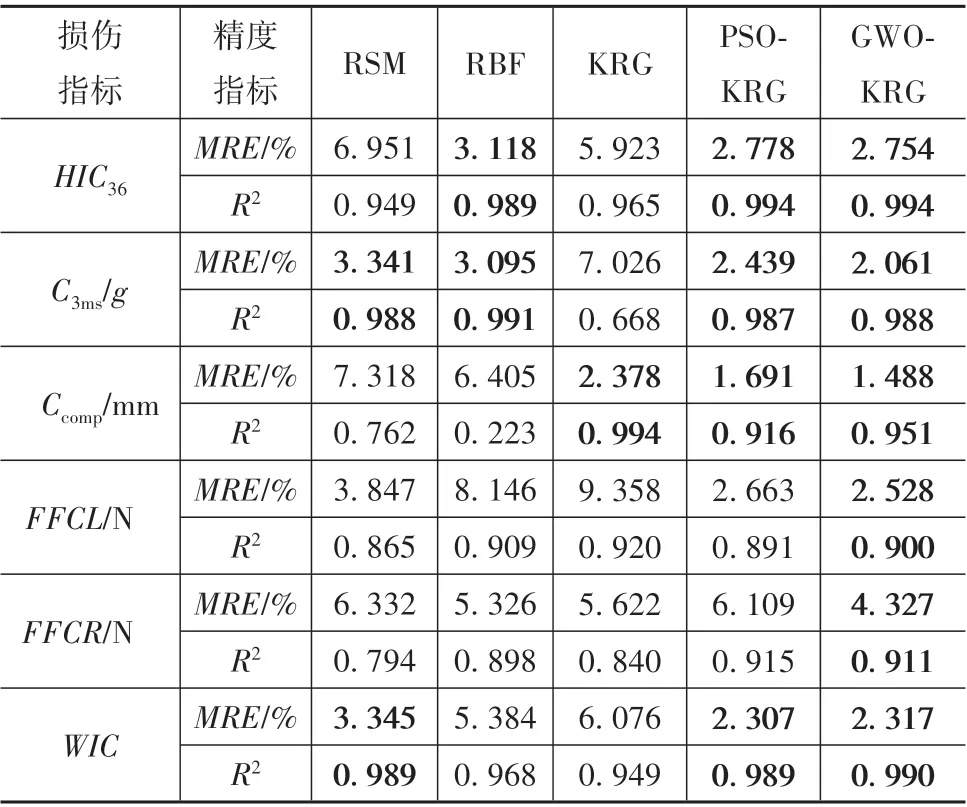
表5 不同近似模型的精度对比

一般地，当R2≥0.9和MRE≤5%时，近似模型具有较高的精度，预测能力较好。可以看出，RSM模型可用于拟合C3ms和WIC，RBF模型可用于拟合C3ms和HIC36，KRG模型可用于拟合Ccomp。3种近似模型中的任何一种均不能同时满足所有损伤指标的精度要求。

已知MRE用于评价近似模型的局部最大误差，而R2用来评价近似模型的整体拟合精度，由表5可知，GWO⁃KRG近似模型和PSO⁃KRG近似模型的全局精度相差不大，但GWO⁃KRG近似模型的局部精度要优于PSO⁃KRG近似模型。针对GWO⁃KRG近似模型，从局部精度来看，除FFCR的MRE小于5%外，其余损伤指标的MRE均小于3%；从全局精度来看，除FFCL和FFCR的R2大于0.9外，其余损伤指标的R2均大于0.95。而对于PSO⁃KRG近似模型，其FFCR的MRE已大于5%，FFCL的R2小于0.9，不满足上文提到的精度要求。因此，GWO⁃KRG近似模型精度最佳，可将其应用于后续的乘员约束系统优化设计。

3.5 优化过程与结果分析

乘员约束系统确定性优化和可靠性优化设计的数学模型分别为

其中，Rj设置为95%，即约束函数的期望可靠度要达到95%以上。在GWO⁃KRG近似模型基础上，采用MIGA对约束系统进行确定性优化设计，并采用蒙特卡罗描述抽样方法在设计空间内采集2 000组样本点，对确定性优化结果进行约束函数的可靠性评估，确定性优化设计结果和可靠度评估结果如表6所示。

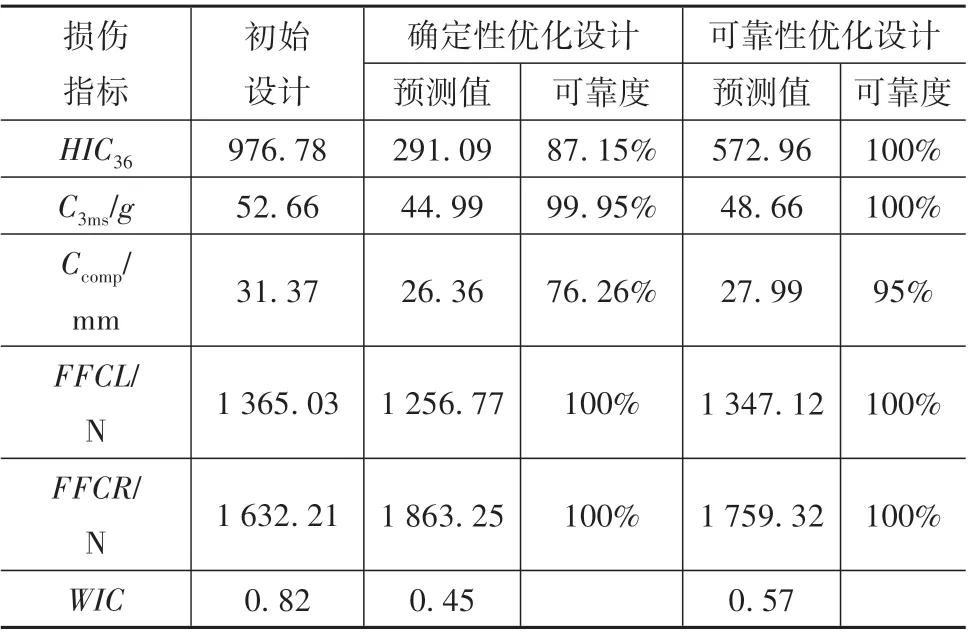
表6 初始设计和两种优化设计结果对比

从表中可以看出，在确定性优化设计结果中，HIC36和Ccomp的可靠度仅有87.15%和76.26%，可靠度远没有达到期望可靠度要求，所以在工程应用中存在设计失效风险。因此，需对约束系统进行下一步的可靠性优化设计。从表6可知，经可靠性优化后，HIC36和Ccomp的可靠度均提高到95%及以上，因此，采用可靠性优化设计得到的设计变量作为优化结果。两种优化设计问题得到的设计变量见表7。

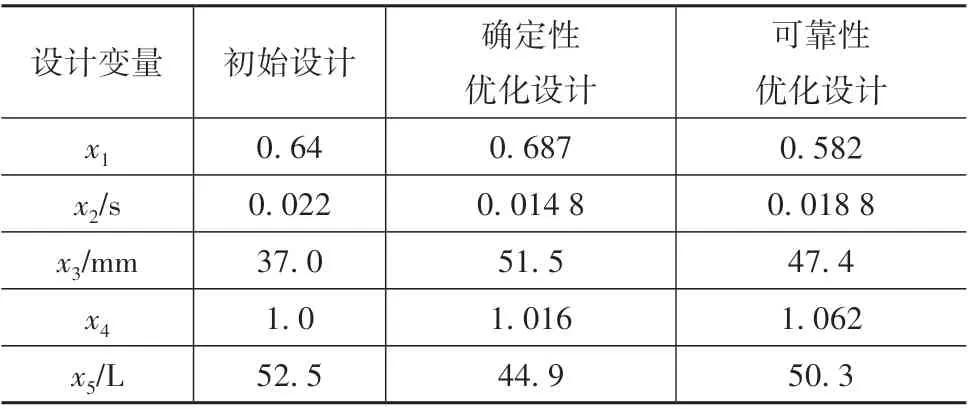
表7 设计变量优化结果对比

3.6 可靠性优化设计结果验证

根据表7修改约束系统仿真模型的设计变量值，并提交计算机进行MADYMO仿真计算，可靠性优化设计方法得到的仿真值如表8所示。由表可知，各损伤指标预测值与仿真值的最大相对误差为3.1%，最小相对误差为1.05%，较小的相对误差证实优化结果有效，所提出的GWO⁃KRG近似模型可信度较高。

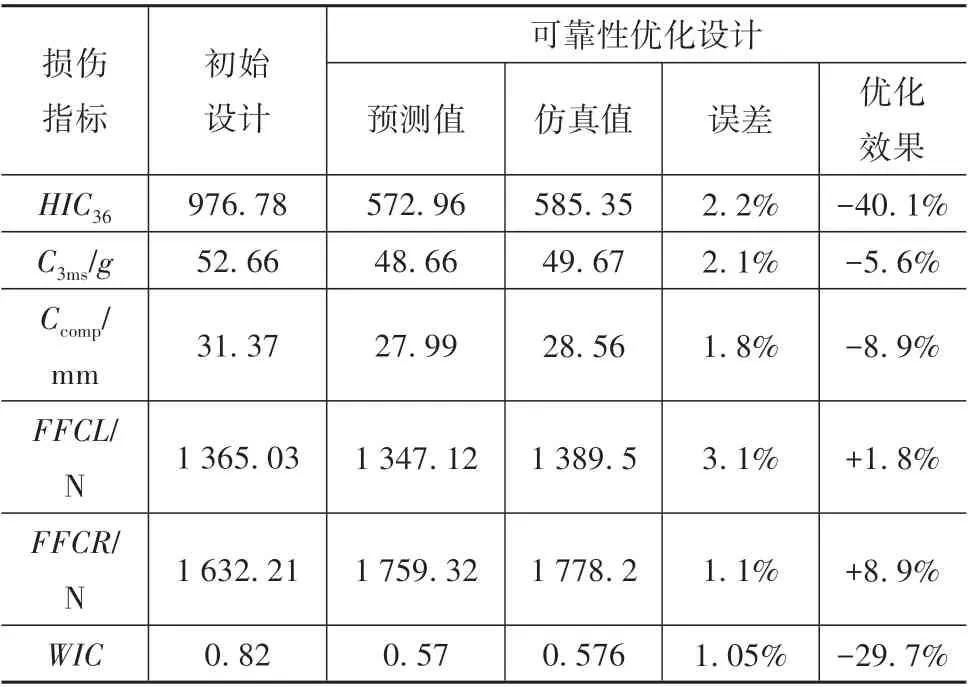
表8 可靠性优化设计验证和优化效果

与初始设计相比，HIC36优化效果明显，降低了40.1%，Ccomp和C3ms分别降低了5.6%和8.9%，虽然FFCL和FFLR相比初始设计均有少量增加，但优化目标WIC降低了29.7%，表明乘员总体损伤降低，优化后的乘员约束系统能起到良好的保护效果。

图4示出初始设计、确定性优化设计与可靠性优化设计结果下，假人头部X向加速度和胸部压缩量仿真验证曲线的对比。相比初始设计，确定性优化设计和可靠性优化设计均降低了乘员损伤，约束系统防护性能均得到提升。虽然确定性优化设计要优于可靠性优化设计结果，但各损伤指标的可靠性得不到保证，因此，最终设计方案选择可靠性优化设计。

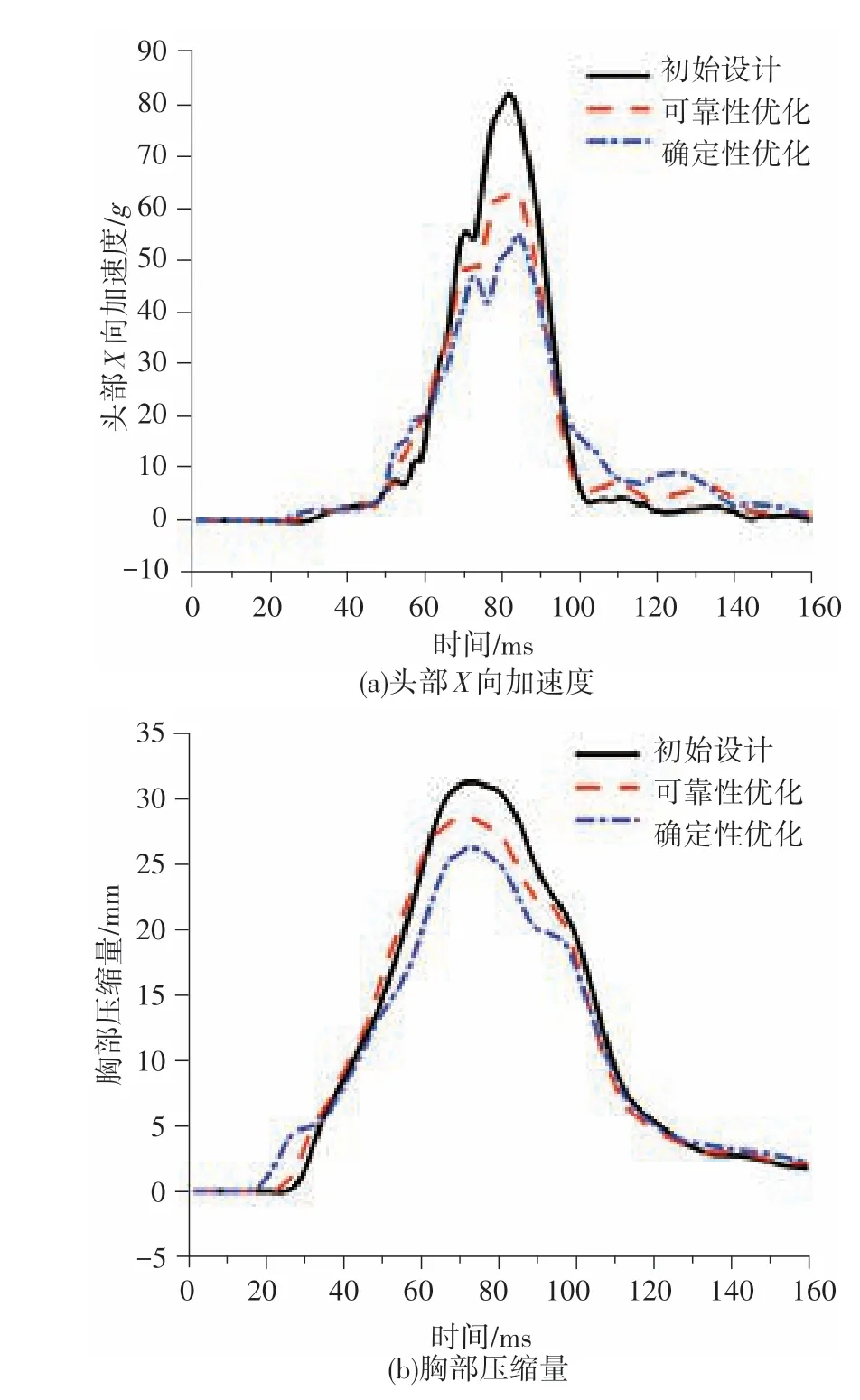
图4 优化结果仿真验证曲线对比

4结论

（1）通过灰狼优化算法对KRG近似模型的相关性参数进行优化，构建了比传统近似模型和PSOKRG模型精度更高的GWO-KRG近似模型，并应用到后续的约束系统优化设计中。

（2）从初始设计、确定性优化设计和可靠性优化设计的仿真对比结果可知，确定性优化结果虽然满足各损伤指标的目标要求，但不满足可靠度要求。可靠性优化设计方法在降低乘员加权损伤准则WIC的同时，使设计可靠性也得到了提高，相比初始设计，WIC下降了29.7%；相比确定性优化，HIC36和Ccomp的可靠度分别提高到了100%和95%。