谐波传动柔轮变形测量误差分析与补偿

杨聪彬，郭庆旭，刘志峰*，张 涛，胡秋实，张雪洋

（1.北京工业大学 先进制造技术北京市重点实验室，北京100124；2.江苏科技大学机械工程学院，江苏 镇江212003）

1 引言

谐波减速器依靠中间柔性部件（柔轮）周期性弹性变形来实现运动及动力传递，当波发生器装配进入柔轮后，柔轮在波发生器作用下产生一定程度的弹性变形，使得柔轮齿与刚轮齿进行啮合［1-2］。但在传动过程中，柔轮齿圈上每个位置的变形是动态变换，会一定程度上影响齿轮产生啮合干涉或者脱离啮合。一般为了便于计算，理论上将柔轮中性层的形变近似作为柔轮的变形，但柔轮在实际的弹性变形是十分复杂的，实际测量柔轮变形函数与理论位置存在较大差异［3-5］，因此精确测量柔轮在波发生器作用下的实际径向变形规律成为当前研究重点。

在实际应用中，虽然测量仪器的精度较高，但测量装置机械机构装配误差难以消除，导致柔轮径向变形测量精度较低，柔轮变形规律的实际检测与理论结果相差较大。目前，针对消除安装误差影响因素进行了大量分析研究［6-9］，但由于波发生器并非标准圆结构，现有的误差补偿方法难以适用，另外柔轮在波发生器作用下发生复杂变形，致使安装误差对柔轮的变形结果产生复杂影响［10-11］，因此国内外鲜有对柔轮变形函数测量中安装误差的研究。本文将基于坐标变化原理提出了柔轮变形偏心测量模型，通过理论偏心模型得到了波发生器与转台中心的安装偏心量、波发生器实际参数，将偏心状态下的柔轮径向变形函数带入误差修正模型，得到消除安装误差下的柔轮径向变形函数，结果表明利用该方法能够有效的解决了柔轮变形在偏心状态下的测量问题，降低实验设备的精度要求，为优化谐波减速器的齿廓参数奠定了实验基础。

2 测量误差分析

2.1 柔轮径向变形理论模型

理论下的谐波减速器柔轮变形是基于三种假设理论下进行分析计算，柔轮径向变形量与波发生器的尺寸参数及转动速度具有一定的函数对应关系，其变形原理如图1（a）所示，柔轮中线在波发生器作用下产生变形，其中细虚线为柔轮变形前中性线，Q(x，y)点为波发生器长轴方向的象限点，P(x，y)为柔轮上变形任意点，实线为柔轮变形后中性线，Q c和Pc分别为变形后的对应点。

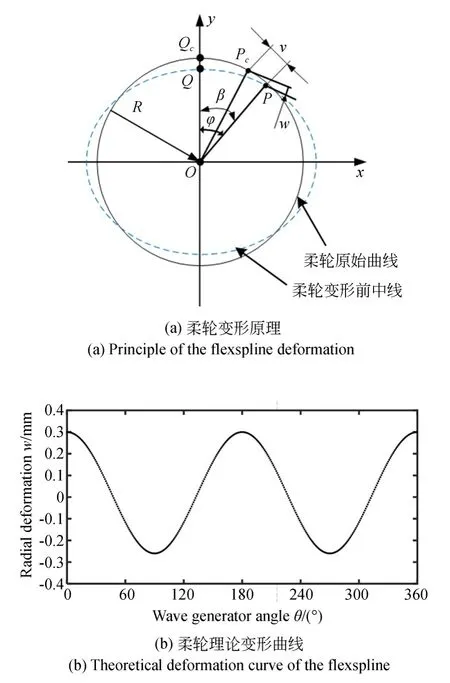
图1 柔轮理论变形图Fig.1 Theoretical deformation diagram of the flexspline

理论柔轮径向变形函数w与转角φ之间对应函数关系：

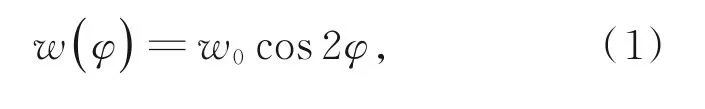
其中：w0为柔轮的最大径向变形量，φ为波发生器的转角。

在波发生器长短轴的最大径向变形量相等的情况下，可用余弦函数代替理论径向变形函数，简化理论共轭齿廓的求解过程，柔轮径向变形理论曲线如图1（b）所示。

2.2 柔轮变形测量误差模型

在理想情况下，被测波发生器按照测量的安装要求，其轴线与精密转台轴线重合进行运动传递，圆光栅精确测量被测波发生器的角位移，通过激光测距仪对柔轮径向变形量进行精确测量，并对信号进行分析处理，准确的得到柔轮的径向变形函数。但在测量机的实际工作中，各个方面都可能存在着相应的误差，导致其测量结果偏差较大［12］。

为进一步研究测量系统误差分布情况，基于多体系统理论与测量系统结果模型，针对转台运动系统进行运动误差模型的分析与建立，其结构与运动误差模型拓扑图如图2所示。

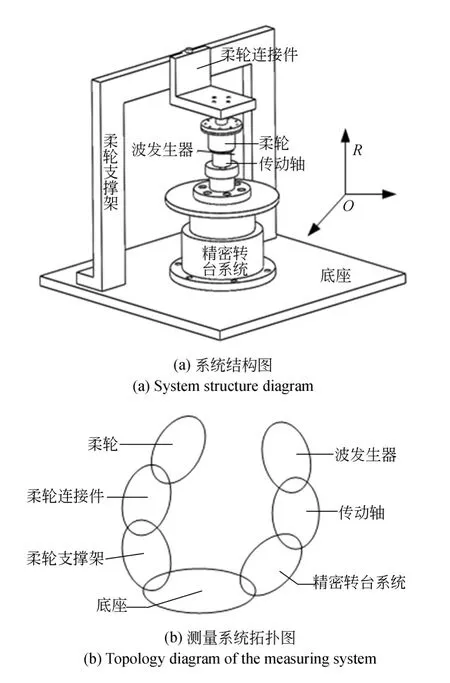
图2 系统结构及拓扑图Fig.2 System structure and topology

基于测量系统拓扑分析模型可知，测量误差主要因素在于测量过程中安装偏心［13］，本文中安装偏心是指波发生器中心与转台回转中心存在偏差。

如图3（a）所示，波发生器与精密转台回转中心存在一定的位置偏心，波发生器以转台中心进行旋转，迫使柔轮发生变形，激光测距仪光线通过波发生器中心，偏心状态下实际测量点的坐标已发生转变，理论测量点（图3中黑色曲线）与实际检测点（图3红色曲线）发生偏移，进而导致其变形结果与理论结果存在较大偏差如图3（b）所示（彩图见期刊电子版）。

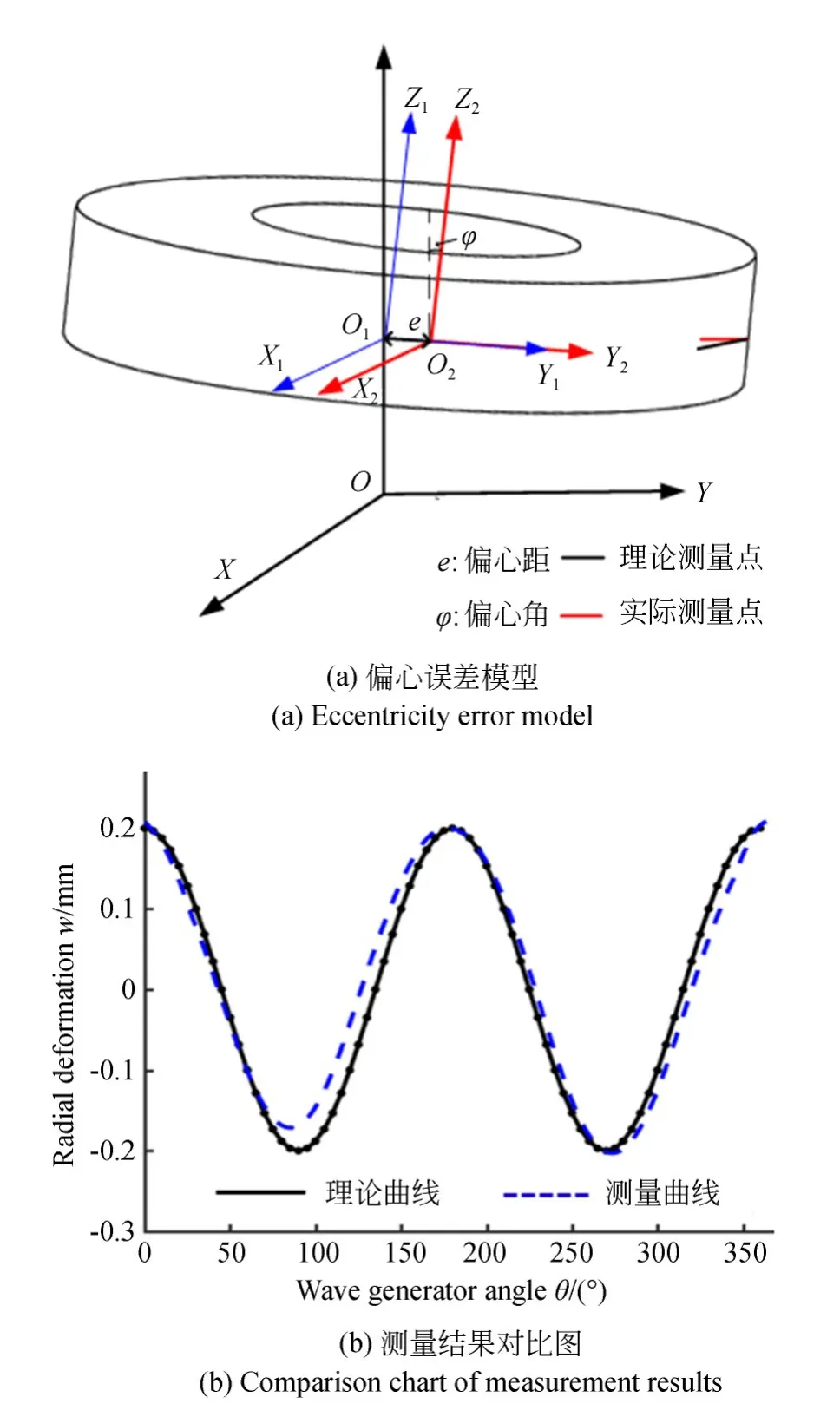
图3 变形函数结果对比图Fig.3 Comparison of deformation function results

在波发生器安装误差作用下，测量结果会使得柔轮变形函数测量结果产生较大的偏差，在偏心位置方向测量结果与实际变形量偏小，反方向测量结果与实际变形量偏大，进而导致变形函数测量幅值与变形规律发生较大偏差，变形量与转角之间的对应函数关系产生转变。

为了去除偏心对柔轮变形测量造成的影响，本文采用矩阵来表示坐标系之间的变换关系，基于坐标变换原理可以得到安装偏心状态下波发生器在转台坐标系下的表达公式为：

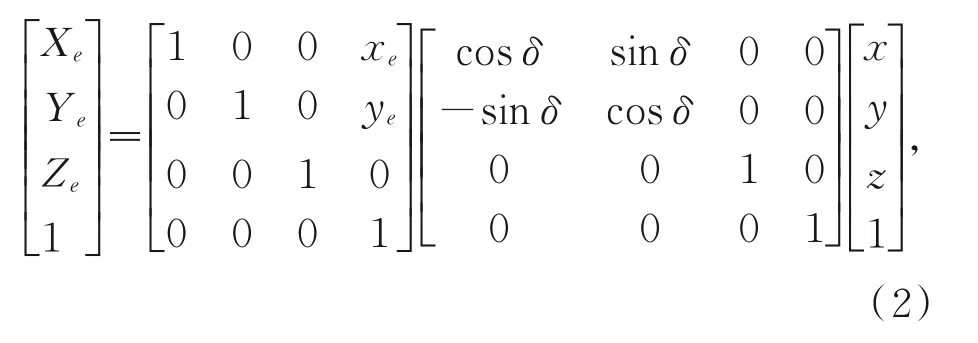
其中：X e为偏心向量的x坐标，Y e为偏心向量的y坐标。

在测量过程中，转台会带动波发生器转动，相当于波发生器各点进行了旋转坐标变换，其旋转变换矩阵为：

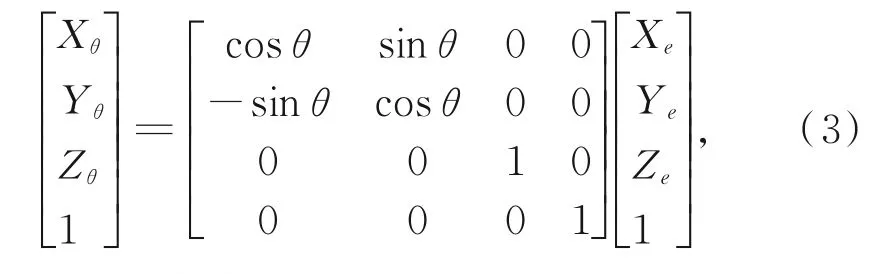
其中θ为转台旋转角度（逆时针为正）。

3 柔轮径向变形补偿方法研究

为解决安装偏心误差导致的检测结果偏差，本文基于坐标变换原理建立安装误差修正模型对检测结果进行补偿。基于偏心状态下理论径向变形量的原理，根据测量点、回转中心与转角之间的函数对应关系，进一步推导出该偏心状态下理论径向变形量表征模型。如图4所示，本文首先建立了理论偏心表征模型，通过实际测量的变形曲线，反求安装偏心量与波发生器的实际参数；其次通过偏心量与椭圆参数建立误差修正模型，对柔轮变形量进行补偿。

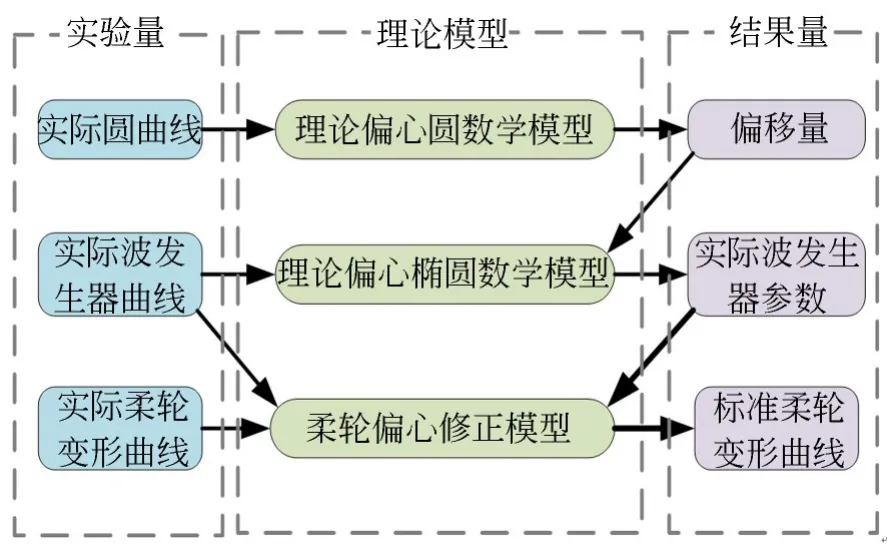
图4 测试方法原理图Fig.4 Schematic diagram of the test method

3.1 偏心量测量模型

通过分析波发生器同轴心的标准圆偏心状态下变形规律，建立安装偏心状态下的偏心测量模型，研究理论状态下标准圆在偏心状态下的变形函数表征方法，其变形原理如图5所示，实际测量点为点A，转动后测量点位置定义为点A1，图中红色虚线表示偏心圆（彩图见期刊电子版）。

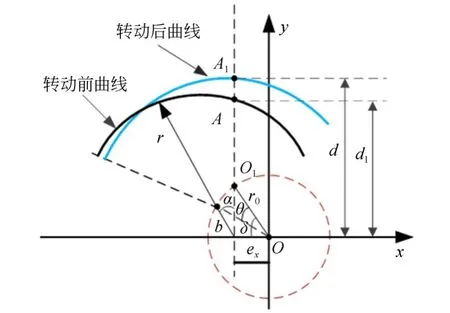
图5 偏心状态圆径向变形模型Fig.5 Radial deformation model of a circle with eccen⁃tric state

在基准坐标系O中，r为标准圆半径，ex为测量线偏移量，r0为偏心圆半径，d0为测量点距离变化量，θ为转动角度，其偏心状态下的标准圆表征函数为：

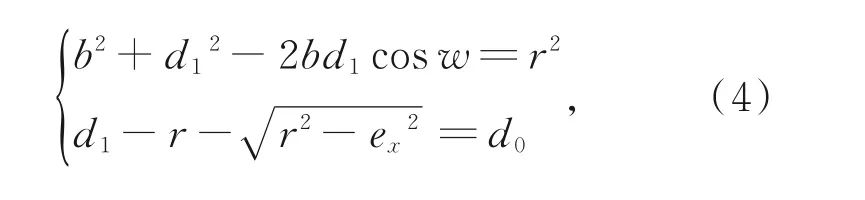
其中：cosδ=。

通过公式（4），可得偏心状态下标准圆径向变形函数为：d0=f(θ)，将实际检测变形曲线分别带入公式（4）中，即可反求出安装偏心量(ex，ey)。

3.2 波发生器参数模型

由于波发生器存在一定的加工误差，为提高测量结果的准确率，需测量实际波发生器参数。通过分析波发生器在安装偏心状态下的径向跳动函数规律，建立波发生器偏心测量模型，研究理论状态下波发生器在偏心状态下的变形函数表征方法。基于坐标变换原理，以波发生器为基准，测量线以偏距圆为中心进行旋转，偏心状态下波发生器变形原理如图6所示（彩图见期刊电子版），起始测量点为B，转动后测量点B1点，图中红色实线表示偏距圆（半径为偏心距ex）。

图6 波发生器偏心变形模型Fig.6 Eccentric deformation model of wave generator

以波发生器中心建立坐标系，θ为转动角度，设转动后测量线与波发生器焦点为B1(x，y)，转动中心O1坐标为(ex，-ey)，偏心状态下波发生器径向理论变形函数为：

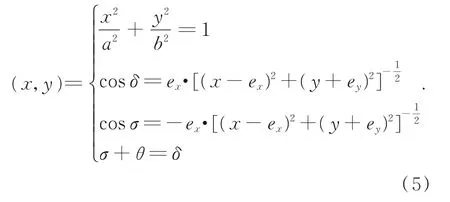
波发生器径向跳动量d：

测量波发生器在偏心状态下的径向变形量d，带入公式（6）中，反求波发生器参数：

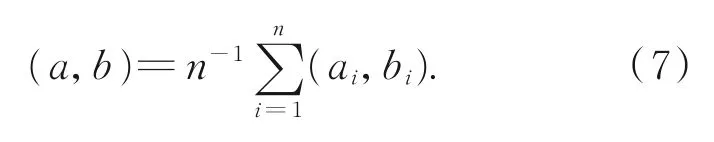
3.3 变形函数误差补偿模型

柔轮在波发生器作用下发生弹性变形，由于安装误差的存在导致测量结果与理论相差偏大，变形函数曲线无法满足谐波齿形设计的要求。

为解决上述问题，研究了谐波传动柔轮变形函数误差补偿模型。本文基于谐波传动原理，首先分析研究了安装误差工况下波发生器表面轮廓曲线函数，建立波发生器偏心补偿模型，获得柔轮在波发生器作用下的径向变形补偿函数；由于安装误差的存在导致柔轮壁厚对测量结果存在一定的影响，如图7（b）所示，使得柔轮壁厚相对于测量点产生了较为复杂的径向位移量，通过研究偏心状态下柔轮壁厚对测量结果的影响规律，建立了柔轮壁厚误差补偿模型。因此安装偏心状态下的补偿模型包含两部分，即波发生器偏心补偿模型与柔轮壁厚误差补偿模型R：

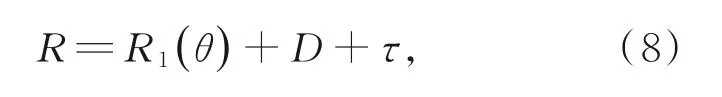
其中：D为波发生器偏心补偿数组，τ为柔轮壁厚误差补偿模型，R1为补偿前柔轮实际测量曲线，R为补偿后柔轮测量曲线。

3.3.1 波发生器偏心补偿模型

柔轮变形误差补偿是以波发生器为研究基准，分析柔轮在波发生器作用下的径向变形量，确定波发生器在偏心状态下进行变形量与理论对应转角下变形量之间对应关系，得到波发生器在偏心状态下的补偿模型D：

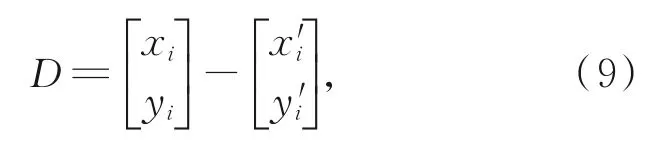
3.3.2 柔轮壁厚误差补偿模型

柔轮壁厚误差补偿模型是指柔性轴承与柔轮得厚度在偏心状态下得误差模型，为标准值与偏心值之间得插值函数τ：

其中：β为理论状态下得壁厚变化函数，β1为偏心状态下得壁厚变化函数。

理论状态下得壁厚变化函数β：

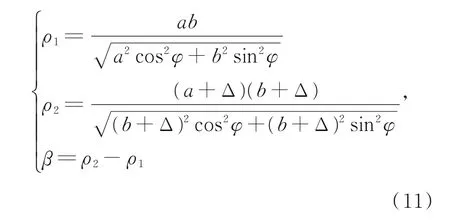
其中Δ为厚度。

偏心状态下得壁厚变化函数β1：

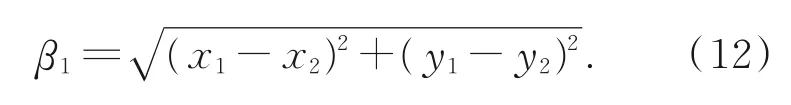
4 实验

4.1 实验装置

本次实验的装置如图8所示，该检测装置包括安装于光学平板上的高精度转台系统、激光测量系统和柔轮固定系统，通过高精度转台系统实现波发生器的安装和360°均匀分度旋转，柔轮通过柔轮支架固定在光学平板上，并通过上下调节实现柔轮与波发生器的接触，激光位移传感器通过传感器支架安装于水平滑台上，并通过前后移动调整实现激光穿过波发生器中心轴线，以此来实现径向变形量的测量。

图8 柔轮变形函数研究平台Fig.8 Platform for flexspline deformation function re⁃search

本次实验转台转速为0.3°/s匀速转动，激光测距仪以100 Hz的采集频率采集。首先，通过上下移动调节柔轮实现波发生器与柔轮分离，前后移动调整激光测距仪实现激光穿过与波发生器同轴心的标准轴中心轴线，测量标准圆变形量，再向上调节激光测距仪实现激光穿过波发生器中心，测量波发生器变形量，最后向下调节柔轮实现柔轮与波发生器的完整接触，测柔轮再波发生器作用下的变形曲线。经调试后转台的定位精度为0.0008°，匀速运动过程中的速度波动为0.01°附近。

表1 谐波减速器参数表Tab.1 Harmonic reducer parameters table

4.2 实验结果

测量与波发生器同轴的标准圆（直径D=30 mm）在三种偏心状态下的径向变形量，经过数据滤波与拟合后，其结果如图9所示，基于理论圆径向变形公式（5），计算出偏心距e为0.245 mm与偏心圆半径r0为0.3275 mm。

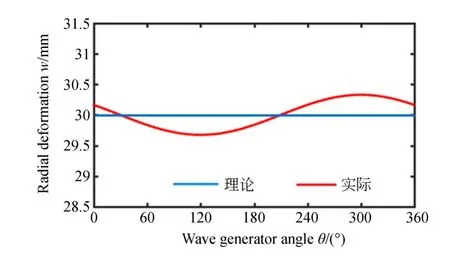
图9 标准圆柱径向变形量Fig.9 Radial deformation of standard cylinder

测量波发生器在偏心状态下的径向变形量，其结果如图10中红色曲线所示，将实际测量参数带入公式（5）和公式（6）中，反求其实际椭圆参数，测量结果如表2所示。图10中理论偏心曲线为实际波发生参数与偏移量(ex，ey)作用下的波发生器径向变形曲线，试验结果可以看出，实际检测波发生器曲线与理论计算偏心曲线基本一致。

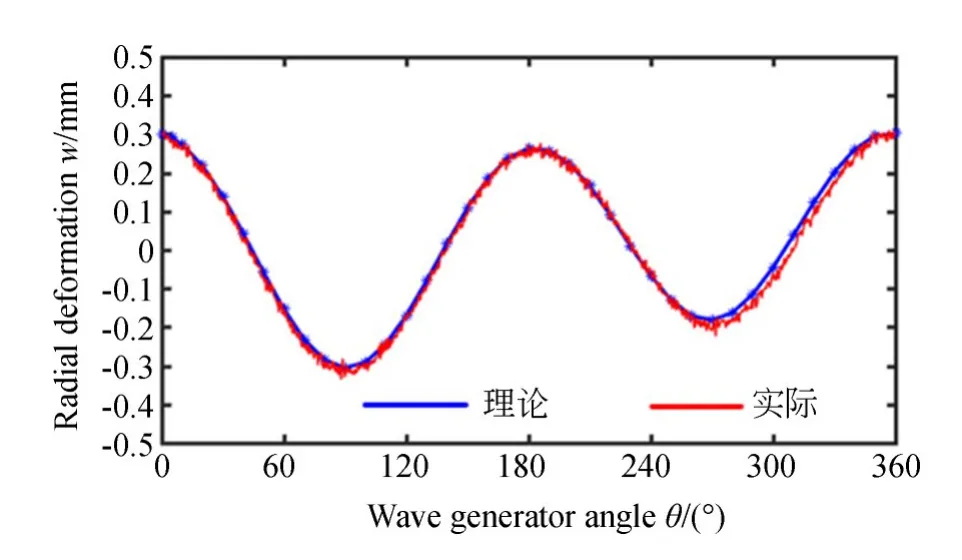
图10 波发生器偏心测量结果Fig.10 Wave generator eccentricity measurement results

表2 波发生器参数结果Tab.2 Results of wave generator parameters（mm）

如图11所示（彩图见期刊电子版），蓝色的理论径向变形按照余弦规律变化，但图11中实际检测的变形曲线（绿色曲线）已经改变，其角度与径向变形量对应关系也发生转变，两个峰谷之间存在0.134 mm的误差。基于谐波传动原理，波发生器转动一周，迫使柔轮测量点产生两次相同变形，且两次变形存在对称关系，因此其变形函数两个峰谷与峰顶是基本一致。由实验结果表明：波发生器转动一周中，柔轮上测量点最小变形量相差0.134 mm，与理论结果（0 mm）相差偏大。

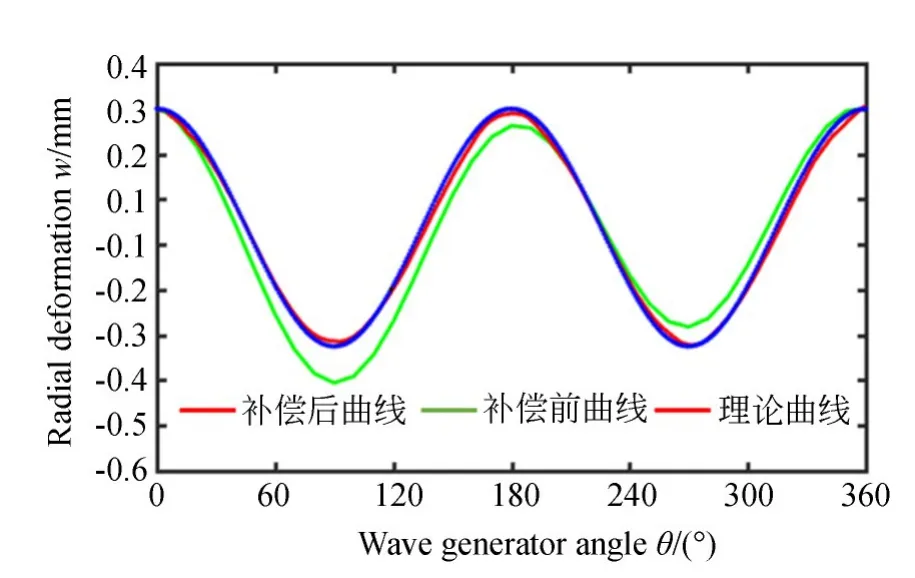
图11 柔轮变形函数对比Fig.11 Comparison of flexspline deformation functions

基于柔轮安装误差补偿模型与偏移量修正后的柔轮径向变形曲线如图11所示，两个峰谷之间存在0.012 mm的误差，实际柔轮的变形频率与振幅与理论模型基本一致，经修正后柔轮径向变形函数测量误差明显减少。如表3所示，在不同偏心位置下该方法测量精度结果基本一致，该误差补偿理论模型正确。

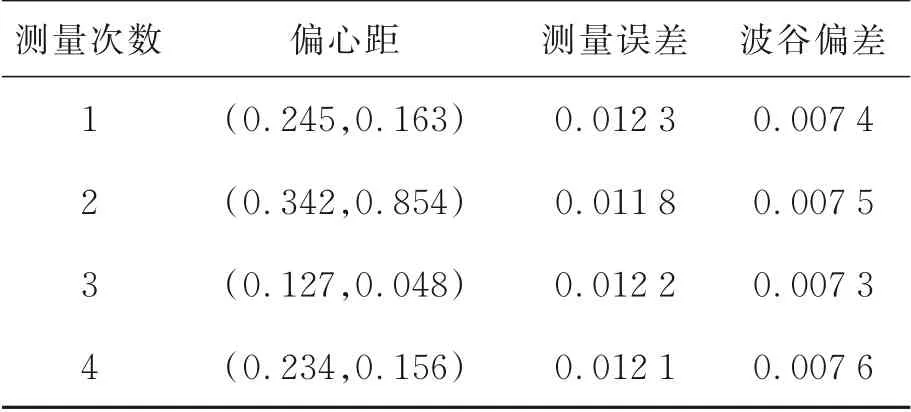
表3 不同位置下测量结果Tab.3 Measurement results at different locations（mm）

5 结论

针对柔轮径向变形测量过程中安装误差导致测量结果偏差较大的技术难题，本文对谐波传动柔轮径向变形测量误差影响因素进行了分析，并研究了安装误差状态下对柔轮径向变形函数测量结果的影响规律，构建了安装误差工况下理论径向变形量的表征模型，提出基于坐标变换原理的柔轮径向变形误差修正方法，消除了柔轮安装误差对变形函数的影响。实验结果证明：安装误差条件下柔轮变形函数峰谷偏差达0.134 mm，与理论相差偏大；在不同偏心位置进行测量、修正补偿后，误差在0.012 mm附近，且柔轮径向变形结果与理论变化趋势一致，基本满足了柔轮变形函数测量的要求。