基于区域选择网络的图像复原及其在计算成像中的应用

吴笑天，杨 航，孙兴龙

（1.长春理工大学光电工程学院，吉林 长春130022；2.中国科学院 长春光学精密机械与物理研究所，吉林 长春130033）

1 引言

计算成像技术是视觉技术不断发展演进中与时俱进形成的新兴交叉学科，一般泛指在成像全链路过程中涉及计算的成像技术。计算成像技术通过全成像链路环节的定向分析及联合优化，主动或被动的形成目标场景和观测图像之间的调制或变换模型，并基于该模型通过数学上逆问题求解反演解算生成所需图像的过程。因此，计算手段的求逆过程是计算成像中的核心问题。图像清晰化技术是计算机视觉领域的热点问题［1-2］，近年来随着计算成像技术的普及深入，也促进着该技术在计算成像领域的发展及应用。本文针对波前编码、单透镜计算成像等计算成像领域的全局一致模糊计算复原背景需求，开展图像清晰化理论方法的研究。

在上述计算成像的子课题领域，波前编码［3］计算成像过程通过添加相位掩模板实现光学调制的过程从而实现成像系统景深的延拓；单透镜计算成像过程［4］则通过带有菲涅尔结构条纹的单透镜实现光学调制的过程，并最终实现单透镜大视场的轻巧成像。该调制过程在图像传感器层面上相当于实施了全局一致模糊化降质的过程，光学调制的引入需要“计算解调”过程实现图像复原处理。因此，一种稳定可靠的全局一致模糊复原算法成为上述领域研究的关键问题。

全局一致模糊化降质的过程，可以建模为清晰图像L与模糊核k的卷积，其数学表达式如公式（1）所示：

其中：O为观察到的模糊图像，L为清晰图像，k为全局一致模糊核，n是加性噪声，“∗”表示卷积算子。图像去模糊过程其实质是在已知模糊图像O而未知的清晰图像L和模糊核k条件下，实施清晰图像L的估计。该问题为全局一致的盲复原问题，在数学上是一个经典的病态问题。

盲复原问题的求解通常通过构建目标函数及添加先验约束以实现病态问题中模糊核估计的可解化，并由此将盲复原问题转化为非盲反卷积问题，从而实现清晰图像L的求解。在这种情况下，模糊核估计的精度直接决定并影响着复原图像的效果。传统优化方法一般通过添加先验约束实施，易出现先验约束失效的情形；通过构建端到端的深度学习复原网络能够获得很好的复原效果，但是实现效果依赖训练过程，限制了该方法的实际使用与普及推广。

为了解决上述问题，本文提出了一种基于区域选择网络的图像去模糊方法。该方法是传统模糊复原与深度学习理论方法的结合。该方法最大的特点在于在传统复原方法的主体基础上，引入了区域选择网络，该网络不直接参与图像端到端的复原，而是对于模糊复原问题中关键因素——模糊求取区域选择进行干预，能够在全局图像中剔除平坦过曝、短小纹理等区域，自动选取最适宜求解模糊核的区域，从而规避了基于优化复原方法先验失效的弊端。

本文方法的实现思路不同于多数深度学习端到端的图像复原方法。本论文所设计的网络虽然需要数据集的预训练，但数据集的制备不依赖波前编码、单透镜计算成像等应用场景的针对性训练，所提出的网络不直接用于图像端至端的生成，规避了其他深度学习方法依赖训练数据的弊端。

试验结果表明，本文提出的方法能够适应全局一致模糊复原任务，区域选择网络鲁棒性较好，能够获得良好的模糊核估计，整体复原结果清晰可靠。

2 背景需求及相关工作

2.1 背景需求

计算成像强调面向成像背景需求的定向化、定制化设计，具有明显的问题导向性特点。目前缺乏统一的数学模型表述。波前编码和单透镜计算成像为计算成像领域的两个子分支。

波前编码成像技术［3，5］是指在在光学成像系统中引入相位掩模板，从而使得像面上的光线不再汇聚为一点，而是变成在一定离焦范围内均匀的细光束。虽然这样的设计会导致探测器直接获取的图像变得模糊，但是这种模糊是计算可逆的，并且能在较长焦深范围内实施这种计算重构，最终扩展的焦深范围可达传统镜头的10倍。图1为文献［5］所示的实现结果，该文的计算解调图像复原算法基于传统的优化方法实现。

图1 计算衍射成像及其图像复原效果Fig.1 Diffractive computational imaging and its restora⁃tion

单透镜计算成像领域旨在解决系统成像的轻巧化设计［6］。设计者通过单一透镜取代传统成像系统的多层镜片光学结构，并将单一透镜的像差优化交付给计算软件，实现清晰图像的恢复。最新的单透镜成像方式由斯坦福大学在2019年提出，该文实现了一种基于菲涅尔结构条纹的单透镜的大视场计算成像方法［4］，该方法在光学设计上在单凸透镜表面利用菲涅尔结构条纹，实现的光学系统像差不随入射角变化，全视场范围内光学系统的点扩散函数（Point Spread Function，PSF）近乎一致但显示出较大的光斑尺寸，便于计算复原的实施与开展，如图2所示。

图2 单透镜计算成像及其复原效果Fig.2 Single-lens computational imaging and its restora⁃tion

该文的计算解调图像复原算法基于生成对抗网络［7］实现端至端的图像复原，数据训练过程较为复杂，需要基于实验室条件下的采集回显系统实现训练数据的制备。

上述两者虽然应用场景有着很大的区别，但是计算成像“光学调制”的过程均体现在探测器直接获取的图像表现为明显的全局一致的成像模糊。计算解调的实施均依赖稳定可靠的全局一致模糊图像的复原算法。

2.2 区域选择的必要性

对于2.1节所述的全局一致模糊的图像复原需求，全局一致模糊核估计是其中的关键环节，而区域选择又是模糊核估计的关键步骤。文献［8］指出从图像中选择最优区域而不是整幅图像，实现模糊核的估计，不仅在成像效果提升上有显著意义，同时还能够降低复原计算的时间复杂度，提升运算效率。

为了证明模糊核求取区域选择对整体复原效果有着直接的影响，本文针对性地做了一组实验，如图3所示。

图3 不同的区域的模糊核估计及其复原效果Fig.3 Different patches lead to different kernel estima⁃tions and different deblurred results.

图3（a）为原始降质模糊图像，在该降质模糊图像中分别选取蓝色、绿色及红色图块区域为模糊核求取区域，使用同样的复原方法［9］获得模糊核估计及整体复原效果分别如图3（b）、图3（c）、图3（d）所示。试验结果表明，图3（d）所示复原效果最优，图3（c）所示的复原效果有少许振铃，图3（b）所示的复原效果则完全失效。由此可见，模糊核求取区域选择对整体复原效果有着直接的影响（彩图见期刊电子版）。

区域选择需要充分利用模糊图像中各类结构信息。然而，并不是所有的模糊图像像素都对模糊核估计有积极的影响。文献［9］指出具有强边缘的区域可以产生较好的去模糊效果。Fer⁃gus等人［10］选择方差大、饱和度低的图像块进行模糊核估计。文献［11］基于一维信号证明了短长度的边缘对模糊求取会产生有不利的影响，模糊核的尺度相对大于目标时，即使具有较强的边缘信息的区域也不能改善模糊核估计的效果。文献［12-14］中提出了多种基于梯度的方法，其试验结果均表明具有特殊梯度模式的显著边缘有利于模糊核估计。Bae等人［15］提出了一种基于非直线度和边缘尺寸的像素级度量来选择图像区域来估计模糊核的方法。Hu等人［8］利用Ga⁃bor滤波器组构造图像特征，并学习二元分类器在条件随机场（CRF）框架内选择好的去模糊区域。CRF模型虽然取得了良好的效果，但由于图像特征的人为设计和计算复杂度的提高，使其应用范围受到了很大的限制。

2.3 运动模糊复原的相关方法

计算成像领域的图像复原需求虽然与运动模糊复原有着本质的区别，但是计算成像采用的复原方法多数源自运动模糊复原领域。一般的运动模糊复原方法主体上可分为两类：基于优化的方法和基于学习的方法。

基于优化的方法侧重于探索图像的各类先验模型。Fergus等人［10］提出了自然图像的稀疏梯度先验。Cho和Lee［13］在多尺度框架中利用图像梯度先验进行图像去模糊处理。Xu等人［11］提出了一种两阶段算法来改进模糊核的估计。Levin等人［9］通过优化最大后验概率（MAP）模型来估计模糊核。Gong等人［16］利用梯度激活方法选择梯度子集进行模糊核估计，而不是使用图像中的强边缘。这些图像去模糊方法对大部分的自然模糊图像是有效的，但是对于特殊类型的图像，如低照度图像、文本图像和人脸图像等等，这些方法都会遇到困难。

为了解决这些问题，学者们提出了许多更加具体的图像先验模型［17-21］。Lai等人［17］利用颜色线来复原图像的边缘。对于文本图像，Pan等人［19］在图像强度和梯度上均引入了L 0正则化先验，提出了一种用于去模糊图像的暗通道先验算法，该算法对低照度图像、文本图像和人脸图像都有很好的复原效果。然而，当图像中以亮度高的像素为主时，暗通道先验就无法有效的估计模糊核。针对暗通道先验算法的缺点，Yan等人［20］进一步提出了一种结合暗通道先验和亮通道先验的极端信道先验，提高了去模糊方法的鲁棒性。Chang等人［21］提出了一种局部最大梯度（LMG）先验，它可以处理各种特殊的图像场景。

随着深度学习在高层次视觉领域的成功应用［22-23］，出现了许多基于深度卷积网络的图像去模糊方法。Schuler等人［24］使用训练好的深度网络估计模糊核，然后使用传统的非盲反卷积方法复原清晰图像。Hradis等人［25］在不假设任何模糊类型的情况下，通过训练深度网络直接重构出清晰的文本图像。Yan等人［26］提出了一个深层卷积网络和一个一般回归网络来分类模糊核的类型并估计其参数。Li在文［27］中利用二元分类网络训练优化模型框架下的先验信息，取得良好的实现效果；Nah［28］提出了一种多尺度卷积神经网络，以端到端（End to End）的方式实现模糊图像的清晰化复原，同时该文发布了GOPRO数据集，广泛用于后续的模糊图像复原的各种对比研究。但此处需要指出的是，该数据集用于研究全局非均匀一致的模糊复原讨论，与本文应用限定的全局一致模糊前提不一致，因此本文后续的研究中没有在该数据集的基础上开展讨论；Zhang在文［29］中提出将RNN的特征提取优势与CNN的权重学习特性相结合，提出了一种可用于非均匀运动模糊端至端的复原神经网络；Kupyn等人在文［7，30］提出用于去图像运动模糊的端到端生成对 抗 网 络（Generative Adversarial Networks，GAN）。

大量的图像去模糊研究致力于利用图像先验假设来提高模糊核估计效果和改进复原图像的视觉质量，而图像结构特征对模糊核估计的影响研究较少。Li在文［27］中虽然同样提出使用二元分类网络，但该文方法使用网络学习的手段实现先验信息的替代。本文方法是通过训练深度二元分类的区域选择网络找出有用的图像结构以进行模糊核估计，进而复原出清晰图像。

3 区域选择网络及复原算法

3.1 复原算法整体流程

基于区域选择网络的图像复原方法主要包括区域选择网络、模糊核估计、非盲图像复原及基于光学衰减模型的图像增强过程，其主要流程参见图4所示。

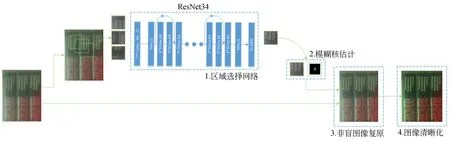
图4 基于区域选择网络的图像复原方法的流程示意图Fig.4 Flow chart of image restoring method based on region selection network

3.1.1 区域选择网络

区域选择网络的主要作用在于对传统方法中模糊核求取区域的选择进行干预，通过构建的深度二元分类网络，能够自动在全局图像中剔除平坦过曝、短小纹理等区域，并选取最优的用于模糊核求取的图块区域；区域选择网络的详细介绍参见3.2节所述。经过区域选择网络的遍历后，区域选择网络会依据图块的输入自动输出最佳的区域选择位置及相应图块B。

3.1.2 模糊核估计

依据该区域选择位置，我们采用文［19］的方法实现该区域的模糊核估计，优化函数如公式（2）所示：

其中：B为区域选择网络推荐的图块，L为推荐图块对应的估计值；项使得估计值图块L与模糊核k的卷积应尽量趋近于观测图块B；为卷积核的正则化项用于促使复原图块L尽量保持梯度稀疏性为该文提出的用于测量暗通道先验稀疏性的正则化项；γ，μ，λ为正则项参数。

3.1.3 非盲图像复原

在已知模糊核估计的基础上，利用文献［18］的方法，实现全局模糊图像的非盲复原过程，该过程首先使用Laplacian先验估计目标图像L l，然后再采用公式（3）所述的迭代过程得到另一个结果LTV。

然后计算二者的差值：L diff=L l-L TV，该差值图像中包含振铃，因此采用双边滤波对其中的振铃进行滤除，得到结果BF(Ldiff)，最后，用L l减去BF(Ldiff)得到最终的去模糊图像Ô(x)。

3.1.4 图像清晰化

从文献［4-5］采集的计算成像系统的试验数据可知，这些计算成像的前端除了引入全局一致图像模糊外，由于光学系统的“不完善”还引入一定程度的衰减。光学系统的衰减虽然在成像链条上与大气衰减不同，但是成像衰减模型是相同的。因此，我们在后端加入基于光学衰减模型的图像增强过程。试验结果表明，基于光学衰减模型的图像增强过程能够良好的改善图像对比度，有利于保持成像系统的颜色恒常性。成像衰减模型如公式（4）所示：

其中：O（x）为经过模糊化消除后的观测图像，J（x）为待恢复的场景图像，t（x）为传输参数，A为背景光参数。

在该衰减模型的基础上，我们使用基于暗通道先验［31］及图像引导滤波［32］的图像清晰化方法实现图像增强过程，如公式（5）所示，暗通道先验及引导滤波的相关原理参见相关文献所述［31-32］：

其 中：Guided(minΩ(x)(Ô(x)))表 征 在 引 导 滤 波优化下的暗通道图像的获取，c为颜色空间，w为防止图像过增强而引入的固定参数，设置为0.9。

在已知传输参数图像的基础上，通过公式（6）实现图像的复原处理。

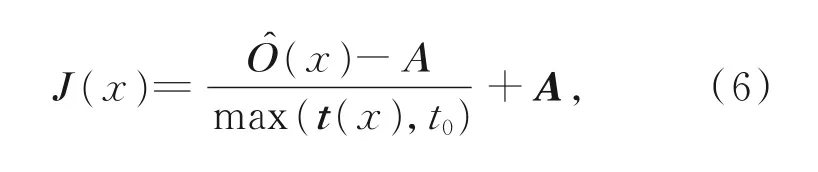
其中：max（t（x），t0）为防止图像过增强而引入的限值操作，t0为固定参数，设置为0.1。

3.2 二元分类网络

受文献［27］利用二元分类网络实现模糊先验评判的启发，本文同样选择二元分类网络作为模糊区域的推荐网络的主体架构。在实际部署应用时，该网络能够对输入图像以步长为5执行全局遍历图块过程，每一个图块均被输入进网络，网络输出为一个概率值，表征这个图块能够用来估计模糊核的可能性有多大。例如如果输出为0.95，则表明该图像块能够估计出好的模糊核的可能性高达95%。最终选择所有输出中概率值最高的图块作为最优的模糊核求取区域推荐。

为了实现这样的二元分类网络，本文基于ResNet34［33］要作为网络架构的主体，合理设计了该网络的损失函数及参数配置，构建了该网络的训练数据集，本文后续章节将详细介绍上述内容。

3.2.1 网络结构

分类问题是机器学习的基本问题。深度学习理论方法对于分类领域有着成功的应用。比较经典的深度学习分类方法包括VGGNet，In⁃ceptionNet， ResNet， DenseNet， Inception⁃ResNet等。

考虑后续算法的工业化移植部署，权衡效果、效率、资源依赖等因素，本文选择ResNet34［33］作为本文网络实现架构的主体。

部署ResNet34网络的主要目的在于实现输入图块是否适宜作为图像模糊核估计区域的判定，即二元判定。以+1作为适宜模糊核估计的区域，以0作为非适宜模糊核估计的区域。

对于ResNet34网络的直接部署不适宜本文的应用场景。常规的神经网络以“分类”作为主要目的，希望强化平移不变性，以期实现对于目标的稳定分类。但是本文的网络结构在于图像模糊核估计区域选择，因此希望弱化网络结构的平移不变性。事实上，如图5所示，对于图5（a）图块平移少量像素确实导致核相似度的显著变化。

图5 移动子窗口的不同模糊核估计Fig.5 Estimated kernels from shifting sub-windows

为了弱化网络的平移不变性，同时也为了保证网络训练的泛化性能和准确性，我们对ResNet34进行改进，将其中的池化层用大步长的卷积层替代，以此来提高网络的分类性能。如此改动的依据来自文献［34］，该文指出深度卷积网络的平移不变性主要来自于池化层。

3.2.2 损失函数

本文对输入图像块及其标签分别用x和y表示，网络参数用θ表示。训练CNNs的目的是要学习训练出公式7所示的映射函数预测出x被分类为y的概率。

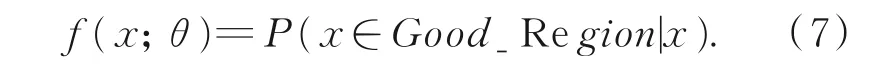
使用二元交叉熵损失函数对深度网络进行优化：

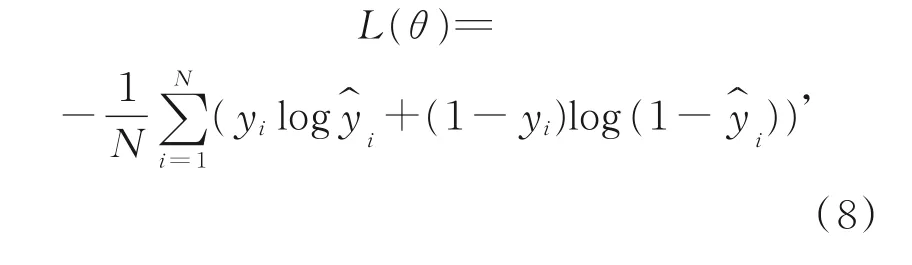
其中：N表示样本的个数，=f(x；θ)，表示网络的输出，本文设置y=1表示有利于模糊核估计的区域，y=0表示对模糊核估计无作用的区域。

3.2.3 数据准备

为了证明本文方法迁移应用的有效性，本文没有在波前编码系统［5］及单透镜的成像系统［4］中实施针对场景部署的数据训练。本文使用运动模糊数据库及相应的模糊图像生成技术实现数据库的构建。使用运动数据库的意义有两点，一则证明本文方法的迁移应用的有效性，二则方便后文与其他的运动模糊方法做对比。

3.2.3.1 图块制备

本文训练数据集主要源自Hu的文献［8］，本文选择了其中30个清晰的图像，包括自然场景、人造场景、文本和人脸图像，以及32个大小、类型不同的模糊核，其尺度从11×11到55×55。采用文献［9］中的方法生成960个模糊图像以供训练，并获取了960个模糊核的真值数据。然后，利用清晰图像和模糊核的卷积，同时加入高斯噪声合成模糊图像，其中噪声的方差为4.0。

在上述960个带有真值模糊核的模糊图像中截取图块作为网络训练的样本。对于每个图像，构造一个尺寸大小为228×228个像素的图像子块集合，其方法如下：从图像的左上点为起始，每次取228×228大小的图像块作为集合中的一个元素，然后再向右平移20个像素，采集下一个图像块，当一行扫描结束后，回到最左侧并向下移动20行作为新的起始点，并按照第一行的方式获取图像子块。实验发现，当模糊核的尺寸小于55×55个像素时，本文设置的图像块的大小足以用来估计模糊核。在给定这些参数的情况下，对于一幅450×450大小的图像，可以获得121个图像块作为训练样本。最终获取了约3万个训练图块。

3.2.3.2 数据标定

在获取的3万个训练图块的基础上，对数据图块进行标定，将数据图块进行正类（+1）和负类（0）的标识，正类表示这些区域可以很好地估计模糊核，而负标记图像区域不能用来估计模糊核。正类和负类的标定依据文［7］中提出的估计模糊核与相应的真值间的相似性方法。

对于从每个图像块使用Yang等人［35］的方法来估计每个图像块的模糊核，使用文［8］方法评估真值相似性。如果相似度大于阈值λ，则将图像区域标记为1，否则将图像区域标记为0。为了便于训练和网络的泛化能力，使正负样本的比例接近1∶1，同时也为了保证模糊核估计的准确性，将阈值λ=0.75。

3.2.4 参数设置

对于模型训练，利用随机梯度下降法（SGD）对网络进行优化。本文使用的批量大小为32，动量设置为0.9，学习率设置为0.001。使用ResNet34的预训练参数作为初始化参数，对网络中被替换的卷积层、第三层、第四层和全连接层进行微调。根据本文实验，20次迭代可以达到收敛。

4 实验结果

4.1 计算成像复原效果及对比

文献［5］提供了几组利用该文波前编码成像系统采集试验数据。本文在未使用该文数据库参与试验训练的基础上，利用本文所述的方法获得的试验效果如图6所示。从图中可以看出，本文方法在细节恢复及颜色对比度方面略优于文献［5］的方法。

图6 单透镜计算成像及其复原效果Fig.6 Diffractive computational imaging and its restora⁃tion

文献［4］实现了基于菲涅尔条纹结构的单透镜成像系统，并提供了几组试验数据。本文同样在未使用该文数据库参与数据训练的基础上，利用本文所述的方法获得的试验效果如图7所示。试验结果表明，本文的方法在图像复原处理效果上与文献［4］的方法接近，但是细节对比处发现，文献［4］的方法在平坦区域形成明显的噪声。

图7 单透镜计算成像及其复原效果Fig.7 Single lens computational imaging and its restora⁃tion

此外，文献［4］的方法实现了良好的颜色白平衡效果，这是端至端的匹配训练过程中由训练数据“驱动”实现的效果，这是该类深度学习复原方法的优势；但同时也是其潜在的劣势。如文献［4］所述，该文需要部署专用的采集回显系统做针对性的训练数据采集，不仅造成了系统批量使用中的诸多不便，也增加了实际使用中由于场景变化而导致的潜在的成像不确定性。

本文提出方法，算法主体沿用传统模糊复原图像清晰化理论方法；所引入的区域选择网络，不直接参与图像端到端的复原，而仅对模糊复原中关键因素模糊区域选择进行干预，以此优化模糊核估计这一关键参数。所涉及的网络虽然需要数据集的预训练，但数据集的制备不依赖场景的针对性训练。从图6～图7的成像复原效果可知，本文方法在场景成像数据未参与训练的基础上，在上述两种计算成像场景中均实现了较好的复原效果，具有良好的复原稳定性优势。

4.2 运动复原相似方法的对比

据调研，在2.1节所述的计算成像领域内基于区域选择网络实施的图像去模糊方法，本文尚属首例，上述领域相关数据试验集的发布也较少，且无真值参考图像，不利于开展对比试验。因此，本文选择在运动模糊复原领域开展基于本文方法的对比试验。

4.2.1 人工及其他区域选择方法的对比试验

现有的区域选择方法主要包括Fergus的文献［10］，Xu的文献［11］，及Hu的文献［8］，及人工交互式的方法。在与人工交互方法的对比中，随机选择几位计算机专业的学生作为试验用户实现人工的区域选择的试验。

对比试验结果如图8所示。人工用户在进行交互式的去模糊区域选择时，倾向于选择具有显著边缘的区域，但人为对于边缘信息的理解并不等同于最适宜区域对图像边缘的预期。Fergus的区域选择算法会因为小边缘的负面影响而导致结果不理想。Xu及Hu的方法在主观复原效果上有轻微的振铃效果。此外需要指出的是，虽然Hu的方法在个别试验数据上选择的结果与本文结果临近，但从复原效果上不及本文方法，这也从另一个角度证明了本文在网络结构设计中充分考量弱化平移不变性而对网络结构的调整而带来的优势。实验结果表明，本文方法的去模糊效果优于其他三种区域选择方法。

图8 不同去模糊区域选择方法的比较-1Fig.8 Comparison on different region selection approaches for deblurring-1.

4.2.2 与整幅模糊估计方法的对比试验

本文还将算法结果与基于整幅图像的模糊核估计方法［19］进行了比较，如图9所示。与全幅图像的去模糊结果相比，本文方法得到了更好的模糊核估计和复原图像。此外，从图9中，我们发现即使训练集不包括饱和图像样本，本文方法仍呈现出良好的复原效果。该实验例表明，本文设计的网络具有良好的泛化能力。

图9 不同去模糊区域选择方法的比较-2Fig.9 Comparison on different region selection approaches for deblurring-2

4.2.3 客观数据对比

为了进行定量对比，使用640张具有挑战性的测试图像进行比较，并展示它们的累积误差直方图。该数据集由文献［36］提供，其中包括来自文献［9］的80幅清晰图像和8个模糊核，定量对比的客观指标为复原误差度量。复原误差度量由文献［9］提出。该度量是用估计的模糊核复原整幅图像的误差和用真实的模糊核复原整幅图像的误差之间的比率，其数学表达式为：

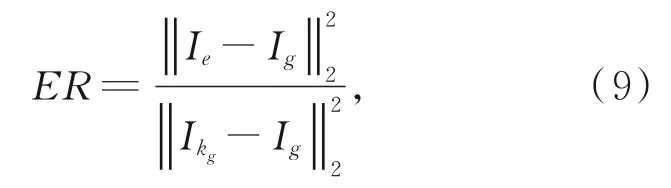
其中：Ie表示用估计出的模糊核复原出的图像，Ikg表示用真实的模糊核复原出的图像，Ig是真实图像。利用该复原误差率的累积直方图来评价该方法的有效性。

此外，将本文方法与区域选择方法［8，10］和全局估计方法［19］，以及基于深度学习的复原方法［27，37］进行了比较。测量每个算法的复原误差率，绘制结果如图10中所示。

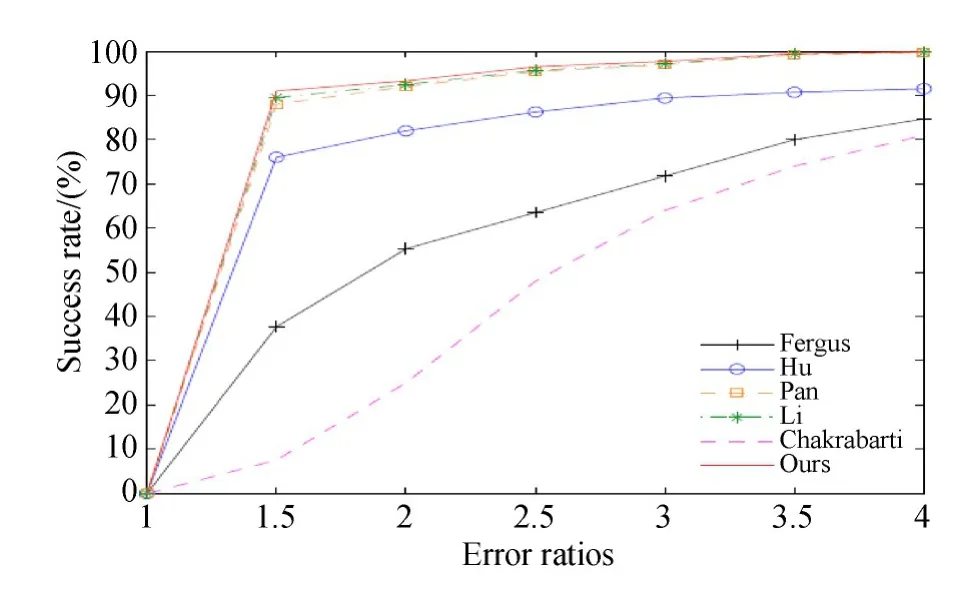
图10 重建误差率成功率Fig.10 Success rate of reconstructed error ratio

从图10可以发现，本文算法优于其他方法。本文方法在ER＞1.5时，成功率一直稳定在90%以上，而区域选择算法［10］在ER=4.0时，成功率也仅仅只有81.4%，另一个区域选择算法［8］的成功率也一直低于90%。而利用整幅图像进行模糊 核 估 计 的 方 法 中，Pan［19］和Li［27］的 方 法 获 得 的曲线和本文方法很接近，但是也略低于本文曲线。

本文同时使用自然图像数据集［38］对算法进行了评估，该数据集包含4幅清晰图像和12个模糊核。将本文方法与Pan［19］和其他三种区域选择方法Fergus［10］，Xu［11］，Hu［8］进行了比较。通过比较每个去模糊图像和沿着相同摄像机运动轨迹拍摄的清晰图像来计算PSNR。如图11所示，本文算法的平均峰值信噪比最高。本文平均PSNR可以达到30.05 d B，这也是五个算法中最高的。

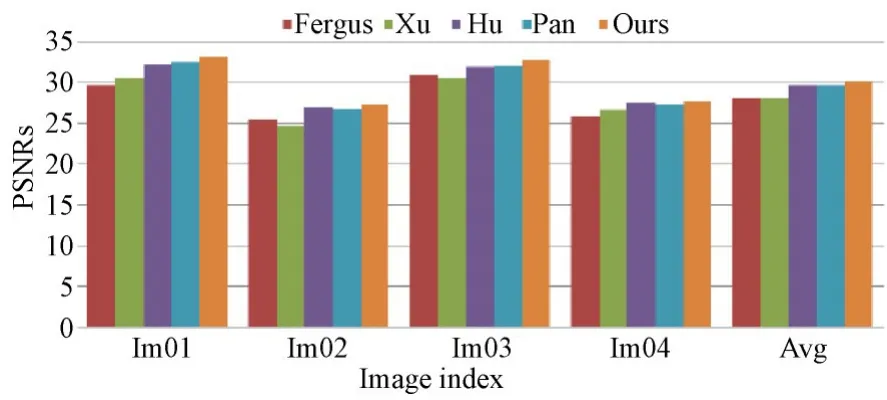
图11 PSNR定量比较试验（横轴下的数字表示图像索引，所有图像的平均PSNR值显示在最右边的列中）Fig.11 Quantitative comparison of PSNR（The numbers below the horizontal axis denote the image index，the average PSNR values of all the images are shown on the rightmost column）

5 结论

本文针对计算成像中波前编码、单透镜计算成像领域的均匀一致模糊复原的成像背景，提出了一种基于区域选择网络的图像去模糊方法。该方法主体基于传统的图像复原及清晰化方法，但是对于复原中核心的模糊核求取问题引入了区域选择网络。该网络不直接参与图像端到端的复原，而是对于模糊复原中的关键因素——模糊区域选择进行干预。该网络能够在全局图像中剔除平坦过曝、短小纹理等区域，自动选取最适宜区域求解模糊核估计。因此，本文所述方法既保有了传统优化方法稳定可靠的优势，又规避了主流深度学习端至端图像复原方法的训练繁琐、成像潜在不稳定性的弊端。

试验结果表明，本文所述方法在计算成像场景数据不直接参与训练的前提下，能够获得边缘良好且复原稳定的处理效果。本文方法较比同类均匀一致运动模糊的复原方法具有一定的优势，客观数据对比试验表明，本文所述方法复原成功率较现有方法至少提升了2.1%，同时平均PNSR至少提高0.5 d B。

在计算成像领域中，均匀一致性模糊复原能够降低计算复原算法的实施难度，但是更为普遍的计算成像场景需求是非均匀一致性的复原问题。因此，在后续的研究中，课题团队将着重在此方向开展后续的算法及理论研究。