利用格型递归最小二乘滤波器组的高光谱图像压缩
2021-07-03薛长斌宋金伟
郑 铁,薛长斌,宋金伟
(1.中国科学院 国家空间科学中心,北京100190;2.中国科学院大学,北京100190;3.国家电网有限公司大数据中心,北京100031)
1 引言
高光谱图像被广泛应用于地质勘探、环境分析、农业监测等领域。随高光谱图像分辨率的提升,图像数据量急剧增加,给传输带宽和存储容量带来巨大挑战。因此,高效的高光谱图像压缩技术必不可少[1-5]。高光谱图像的压缩方法分为有损压缩和无损压缩。有损压缩虽然能达到很高的压缩比,但会破坏数据的细节信息,这对需要精确分析的计算场景是难以接受的,只有无损压缩能保证图像信息的完整性[6-7]。
高光谱图像同时具备空间相关性和谱间相关性。传统的二维图像压缩技术只针对空间相关性,无法利用谱间相关性提升压缩比[8-10]。目前,常见的高光谱图像压缩方法分为变换类、矢量量化类和预测类。其中变换类算法是先将图像从空域映射到变换域,使用较少码字表示图像的主要信息,随后再对细节量化编码,因此常用于有损压缩[11]。矢量量化类算法的计算复杂度会随维数增加呈现指数级的增长,庞大的计算量限制了该类算法的实际应用[12]。预测类算法先使用预测器计算待测像素点估计值与实际值的差异,去除图像的相关性,再针对预测误差做压缩编码。这类算法在获取良好压缩结果的同时保持较低的算法复杂度,逐渐成为国内外研究热点[13]。
Mielikainen等人提出基于查找表(Lookup Table,LUT)的预测方案[14],该方案将前一波段中与当前像素点具有同位坐标的像素作为索引,使用查找表返回预测结果。H.Bormin等人改进LUT的预测方案,提出局部平均谱间尺度变换的方法(Locally Averaged Inter-Band Scaling-LUT,LAIS-LUT)[15]。该方法先计算待测像素点的LAIS估计值,随后在两个查找表中索引与LAIS估计值最接近的值并作为预测结果。基于LUT的压缩方法虽然具有良好的预测效果,然而它消耗大量的内存资源,不适用于星载图像压缩系统。
聚类差分脉冲编码调制(Clustered Differ⁃ence Pulse Code Modulation,C-DPCM)是一种将聚类和线性滤波器相结合的预测方案[16]。该方法首先利用k-means聚类算法将光谱矢量做聚类处理,提升同类矢量间的相似度。随后,采用预测长度固定的线性滤波器做预测压缩。具有自适应预测长度的聚类算法(C-DPCM with Adaptive Prediction Length,C-DPCM-APL)是C-DPCM算法的扩展,它通过搜寻线性滤波器输入的最优预测长度获得良好的压缩效果[17]。但该方案的计算复杂度较高、消耗资源较大,更适合被应用于离线压缩场景。
空间数据系统协商委员会(Consultative Committee for Space Data Systems,CCSDS)提出基于最小均方误差滤波器的快速无损(Fast lossless,FL)算法[18],该算法利用先前的波段预测当前像素,并在线性预测过程中自适应改变预测系数。三阶谱间预测器(The third-order interband predictor,IP3)[19]由两阶段预测器和熵编码组成,通过谱间预测器和反向像素搜索(BPS)方案计算最终预测值。宋金伟等人提出基于递归最小二乘法(Recursive Least Squares,RLS)的压缩方案,该方案先将待测像素点做空间滤波,再利用固定长度的递归最小二乘做谱间预测[20]。由于递归最小二乘滤波器较最小均方误差滤波器的收敛速度快,因此其压缩结果要优于FL算法。高放和郭树旭提出自适应预测波段的传统最小二乘压缩算法(Cnventional Recursive Least-Squares Predictor with Adaptive prediction bands,ACRLS)[21]。该文献指出不同待测波段的最优预测长度是不尽相同的,并通过穷举法搜索每个待测点RLS滤波器的最优预测长度,获得良好的压缩效果。但该算法的计算复杂度过高,消耗大量的计算时间。宋金伟等人提出的快速RLS(Fast Adaptive-Length-Prediction RLS,Fast-RLS-ALP)预测算法[22],相较于传统RLS算法,该算法充分利用已知波段的滤波器做前向预测,降低计算复杂度。但该算法的空间预测方案比较简单,且谱带间滤波器只使用固定长度的预测方案,因此压缩结果并不突出。
本文提出一种基于格型递归最小二乘滤波器组的高光谱图像无损压缩方案(RLS Lattice Filter Group,LFG-RLS)。该压缩方案采用的格型滤波器组充分考虑最优谱带预测长度对预测效果的影响,合理地为每个谱带选择最优滤波器,并利用其链式序列更新的特点,对滤波器组分类、简化,大幅度降低计算时间。
2 压缩方案介绍
本文提出的压缩方案分为预测器和编码器,其中预测器包含谱带内预测和谱间预测两个阶段。对于高光谱图像的每个谱带,首先使用单边高斯预测器做谱带内预测,得到谱带内预测误差。其次,采用格型滤波器组筛选每个谱带的最优滤波器,使压缩结果接近最优,并根据格型滤波器组链式更新的特点,对最优滤波器做进一步筛选,大幅度降低计算时间。最后,利用算术编码器对预测误差做压缩编码,得到压缩码流。本文的压缩方案结构图如图1所示。
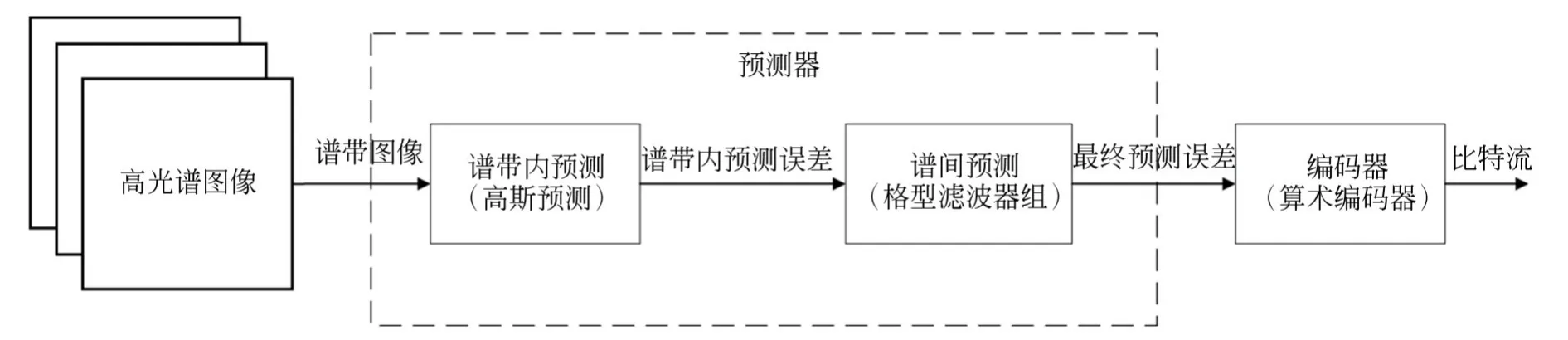
图1 压缩方案结构图Fig.1 Algorithm structure chart
2.1 谱带内预测
高光谱图像可被视为一组三维数据,设其尺寸为W×H×N(行×列×波段),本文使用sz(x,y)表示第z波段中第x行第y列像素点的灰度值,或使用sz(n)表示z波段中第n个像素点的灰度值,其中n=W×y+x。并将具有相同y坐标的平面称为线谱平面(Line-Spectral Plate,LSP),如图2所示。
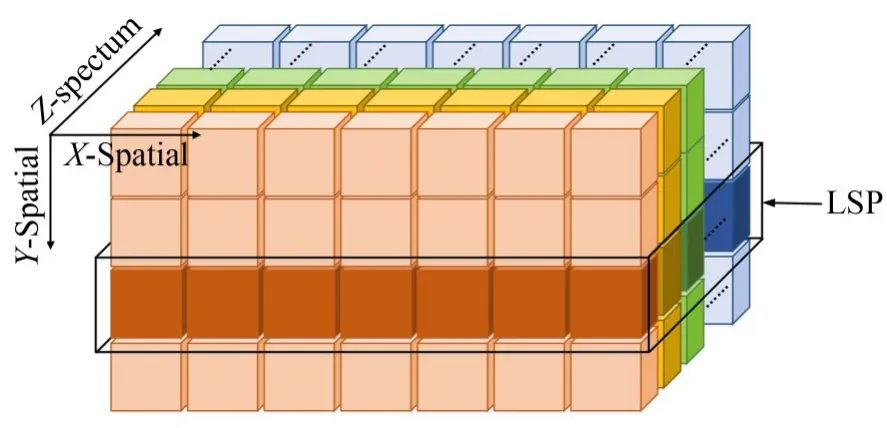
图2 线谱平面Fig.2 Line-Spectral Plate
在谱带内预测阶段,通过对待测像素点的上下文像素做预测运算,计算谱带内预测误差,从而去除高光谱图像的空间相关性,其中待测像素点的上下文窗口如图3所示。ACRLS[21]和Fast-RLS-ALP[22]算法分别采用24邻域和4邻域均值的预测方式去除空间冗余信息。
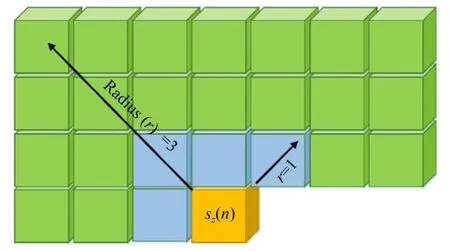
图3 待测像素点的上下文窗口Fig.3 Context window of current pixel
因待测像素点与上下文像素之间的相关性随距离的增加而减小,高斯预测器被用于谱带内预测。为保证预测过程的因果性,即使用已知像素点预测当前待测点,采用的单边高斯预测器如式(1)所示:

其中:
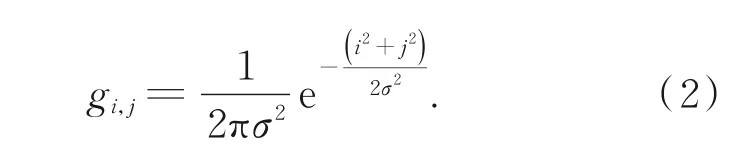
则 当 前 像 素 点 的 估 计 值ŝz(x,y)如 式(3)所示:

z波段第n个像素点的谱带内预测误差d z(n):
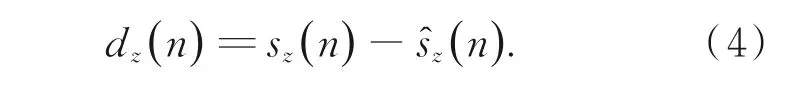
对于首个波段的预测误差d z(n)直接使用编码器压缩编码,其余波段则使用格型滤波器组去除谱间冗余信息后再编码。
2.2 谱带间预测
高光谱图像在光谱维度上具有较强的相关性,但受噪声影响,各相邻波段谱间相关性的强弱不同。因此,RLS滤波器的预测效果与预测长度(待测像素点滤波器输入向量的长度)并不总是呈现正相关的关系,对于部分谱带,较短的预测长度可以获得良好的预测效果[17,21],合理地为每个谱带的滤波器选择预测长度,是提升压缩算法性能的关键。
2.2.1 格型滤波器组
对于波段按行交叉格式的高光谱图像,在谱带间预测过程中,z波段第n个像素点共使用z-1个不同预测长度的滤波器F z,i(n)(i={1,2,…,z-1}),其中下标“i”被用于标识不同预测长度的滤波器。则F z,i(n)的输入向量xz,i(n)=[d z-i(n),…,d z-1(n)]T,对应的权重向量w z,i(n)=[wz-i(n),…,w z-1(n)]T,期 望 信 号为d z(n)。则F z,i(n)的计算过程如公式(5)~公式(13)所示。
首先计算Fz,i(n)的谱带间预测残差:
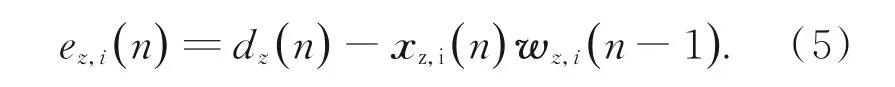
预测误差方差的累计值vz,i(n):
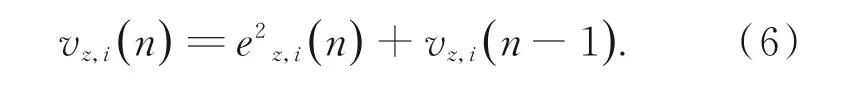
设:
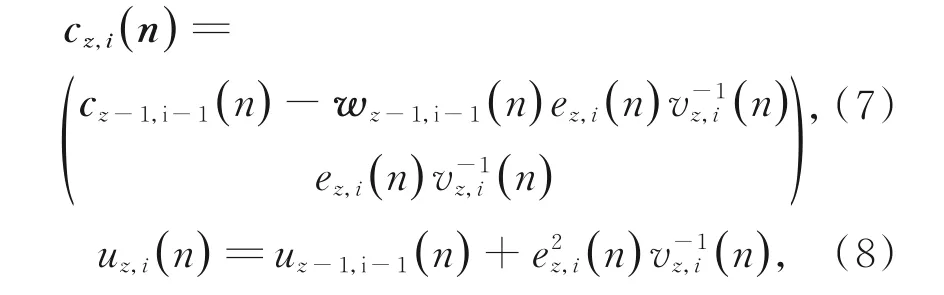
其 中:cz,i(n),uz,i(n)分 别 为 滤 波 器 的 投 影 向 量、投影值。
滤波器的增益为:
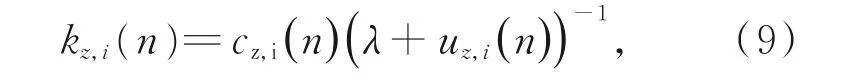
则权重向量w z,i(n)的递归更新如式(10)所示:
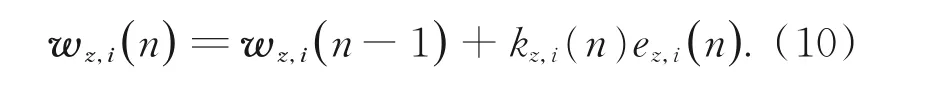
为确保滤波器的收敛性及屏蔽一些异常的像素值,当滤波器阶数≤3时,投影向量cz,i(n)及投影值uz,i(n)采用传统RLS滤波方式更新,如式(11)~式(13)所示。
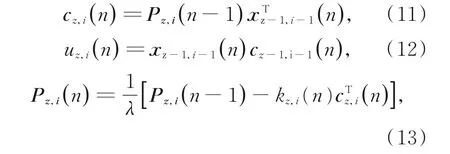
其中:根据文献[21]RLS滤波器敏感性测试结果初 始 化 遗 忘 因 子 为λ=0.9995;w z,i(0)=[0,0,…,0]T。依 据 上 述 更 新 过 程 可 知:F z-i+1,1(n),…,F z,i(n)是依次递归更新的,这组具有前向迭代更新关系的滤波器称为链式序列。因高光谱图像共有N个波段,首个波段的谱带内预测误差直接使用编码器压缩编码,本文提出的格型滤波器组中共包含N-1条链式序列,如图4所示,为简洁表示,省略每个滤波器的部分符号(n)。图中每一列表示同一待测点不同预测长度的滤波器;箭头表示同一条链式序列内滤波器的迭代更新方向,将用于迭代更新F z,i(n)的链式序列记作集合Ωz,i(n):
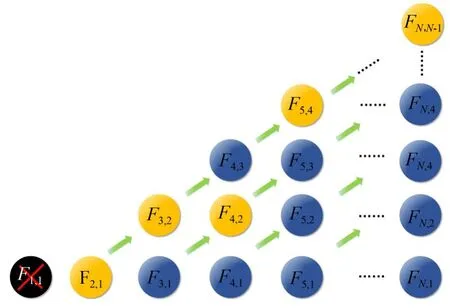
图4 格型滤波器组的链式序列Fig.4 Chain sequence for filters
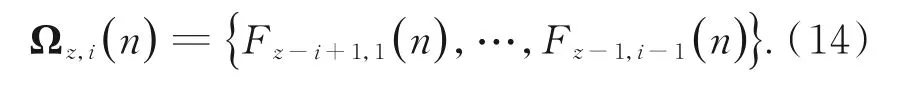
格型滤波器组在预测过程中,v z,i(n)被用于衡量同一待测点不同预测长度滤波器的预测精度。预测误差被视为服从均值为0的高斯分布,其信息熵H与方差σ2呈现正相关关系,如式(15)所示:
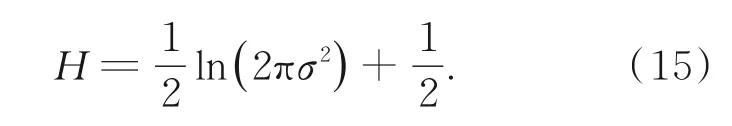
因此,在波段z第n个像素点的不同预测长度滤波器中,具有最小预测误差方差累计值v z,min(n)的滤波器称为最优滤波器F z,opt(n),其中v z,min(n)=min{v z,1,…,vz,z-1(n)}。最优滤 波 器的预测长度被称为最优预测长度,记作L z(n)。
若直接使用格型滤波器组顺次计算每个待测点不同预测长度的滤波器,虽然能获得最佳的预测效果,但耗费过长的计算时间。在此,通过对滤波器收敛性的考察,优化了格型滤波器组的更新方式,为衡量z波段第n个与第n-1个待测点权值的变化情况,定义相邻滤波器权值的距离(Distance of Weights,DOW)
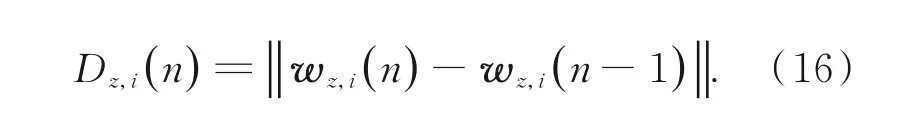
以AVIRIS 2006高光谱图像集中Yellow⁃Stone 0校准图像为例,滤波器F223,222(n)的DOW随迭代次数的变化趋势如图5所示,随迭代次数的增加,各个滤波器具有明显的收敛趋势。因此,同一谱带不同预测长度滤波器参数v z,i(n)的排布次序趋于稳定,最优滤波器搜索阶段可以被提前终止,后续谱带的最优滤波器被认为是相同的。
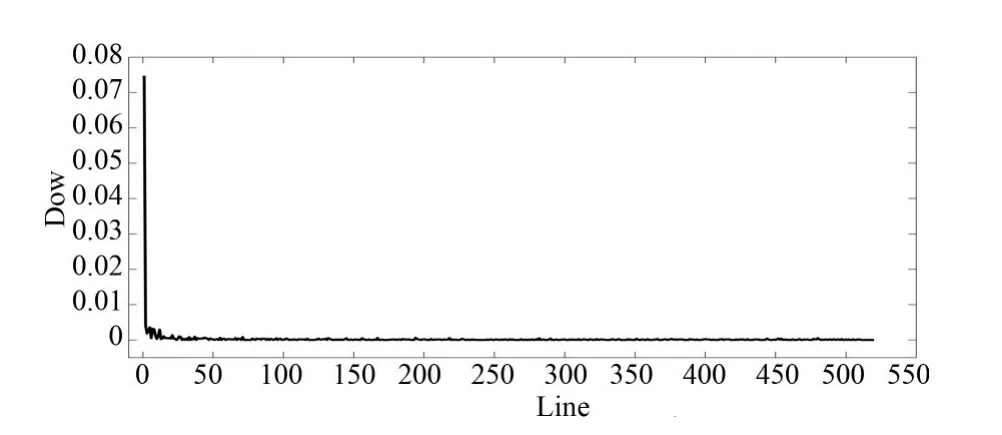
图5 不同LSP中相邻滤波器权值的距离Fig.5 DOWsof filtersfor different LSPin calibrated image
引入限定迭代次数的阈值T,当n=T时,先计算波段z第T个待测点的最优滤波器F z,opt(T),随 后 更 新 其 链 式 序 列 集 合Ωz,opt(T)。为统计当前谱带所有待测点最优滤波器的链式序列,使用最优滤波器集合Ω表示每个待测点Ωz,opt(T)(1<z≤N)的并集。当n>T时,最优谱带搜索阶段将被终止,进入快速预测阶段,只有位于Ω中的滤波器需要被持续更新。为直观地描述格型滤波器组的预测过程,算法流程图如图6所示。

图6 格型滤波器组的预测过程Fig.6 Prediction process for Lattice Filters
在上述格型滤波器组的更新过程中,当n>T时,位于Ω中的滤波器需要被持续更新。因此,越多的滤波器位于同一条链式序列中,待更新滤波器的数量越少,消耗的计算时间越短。
2.2.2 提升策略
以校准后Yellow Stone 0图像的400th和500thLSP为例,各谱带的最优预测长度如图7所示,除个别受噪声影响的波段外,大多数谱带的最优预测长度随z的增大而增大。因此,可以经筛选分类,使更多的待更新滤波器处于同一链式序列。本文提出最长更新规则:若多个滤波器的最优预测长度相近时,应将具有最长链式序列的滤波器视为最优滤波器。为简化分类操作,若z波段第n个待测点的最优滤波器预测长度L z(n)≥时,则将最长链式序列中的滤波器视为最优滤波器;否则vz,i(n)最小的滤波器被用于迭代计算。
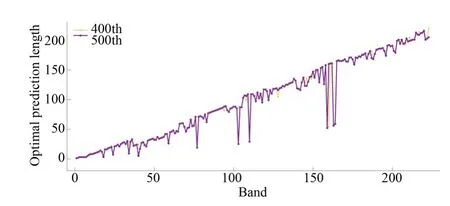
图7 不同谱带的最优预测长度Fig.7 Optimal prediction length of different band
此外,在文献[21]中,高放等人发现对于同一成像系统拍摄的高光谱图像集,其最优预测长度高度一致,并建议将首个图像的最优预测长度直接应用于预测该场景的其余图像。该加速方案同样应用于本文算法,记为RLS Speed Lattice Filter Group(SLFG-RLS)。
2.3 算术编码
本文采用算术编码器做压缩编码。因最终预测误差数据是用16位表示的,故算术编码的码表需要使用65536个符号。根据预测残差的概率分布,大多数符号没有被使用,故采用自适应码表。初始的码表包含0和ESC两个符号。当需要对一个新符号编码时,编码器先使用ESC的概率对其编码,随后再更新码表便于后续编码。
3 实验结果与分析
本文压缩方案中的所有程序均在实验平台(Intel i7-7700k CPU 4.20GHZ/16GBRAM)中以C语言进行编写、测试。CCSDS的多光谱和高光谱数据压缩工作组提供的AVIRIS 2006高光谱图像数据集作为本文算法的测试数据源。
测试图像集包括5个16位校准和5个16位未校准的场景,每个场景包含512行,224个谱带的数据,其中校准与非校准场景每行分别有677和680个像素点。在此,将场景名称的首字母及其序列号用作缩写,例如:Yellowstone scene 0记作YS_SC0。
3.1 高斯预测器的参数选择
在谱带内预测阶段,为便于计算,本文采用整数型的单边高斯预测器。本文将均值滤波器及不同参数的高斯预测器做测试与比较。以YS_SC0场景为例,实验结果如表1所示。
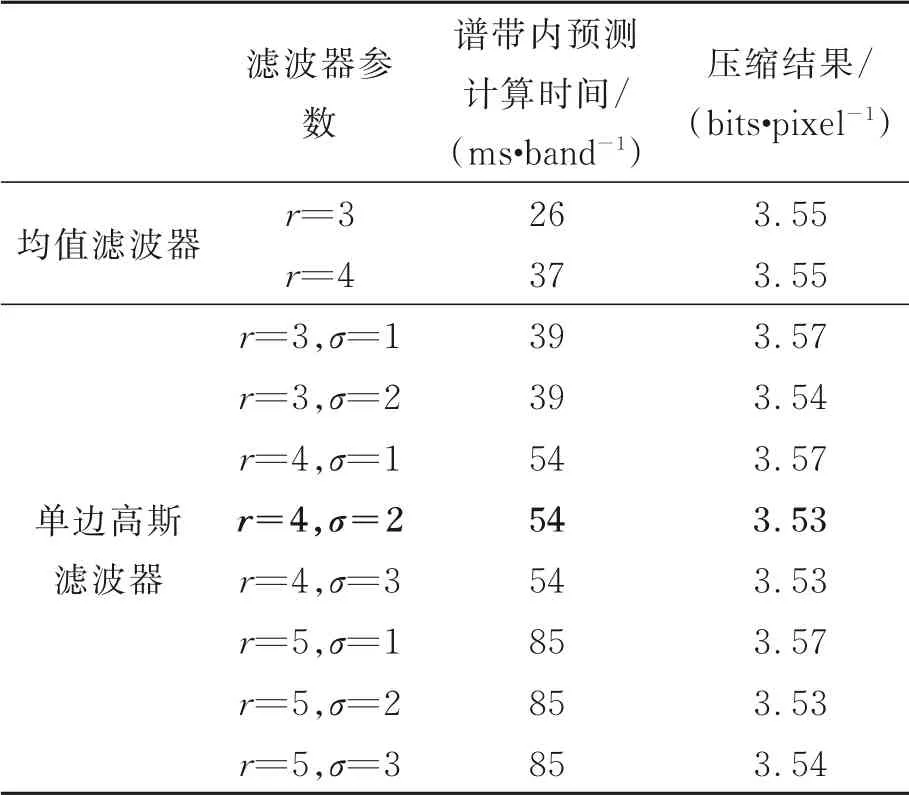
表1 不同参数的高斯预测器Tab.1 Different parameters in Gaussian predictor
在窗口半径相同时,对于每个谱带高斯预测器比均值预测器多消耗十余毫秒的计算时间,但高斯预测器能获得更佳的压缩效果。对于高斯预测器,当σ≥2时,能获得较好的压缩效果;当窗口半径r≥4时,预测器的压缩效率没有明显提高,但时间复杂度却骤增。考虑到算法的计算复杂度和实时性,最终选用σ=2,r=4作为单边高斯预测器的初始化参数。
3.2 迭代阈值的选择
随迭代次数的增大,滤波器的最优预测长度趋于稳定。以校准后YS_SC0场景中209,140,94,49波段的最优滤波器为例,图8展示不同LSP的最优预测长度L z(n)。
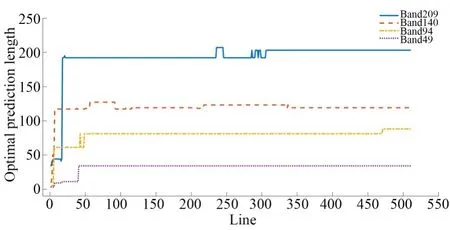
图8 不同LSP的最优预测长度Fig.8 Optimal prediction length for different LSP
当迭代次数的阈值T≥50 LSPs时,最优预测长度波动很小。根据公式(15)和公式(16),随滤波器迭代训练次数的增加,收敛趋势愈加明显,同一谱带不同预测长度滤波器参数vz,i(n)的排布次序及滤波器最优预测长度波动渐小,趋于稳定。为量化描述迭代阈值对算法的压缩结果、计算时间的影响,以校准后YS_SC0场景为例,表2展现格型滤波器组在使用提升策略前的压缩结果、计算时间与T的关系。
从表2中可知,当T≥50 LSPs时,算法的压缩结果趋于固定,但计算时间急剧上升。考虑到实际压缩结果和时间复杂度的双重影响,本文算法将参数T初始化为50 LSPs,从而保证良好的压缩效果以及较低的时间复杂度。
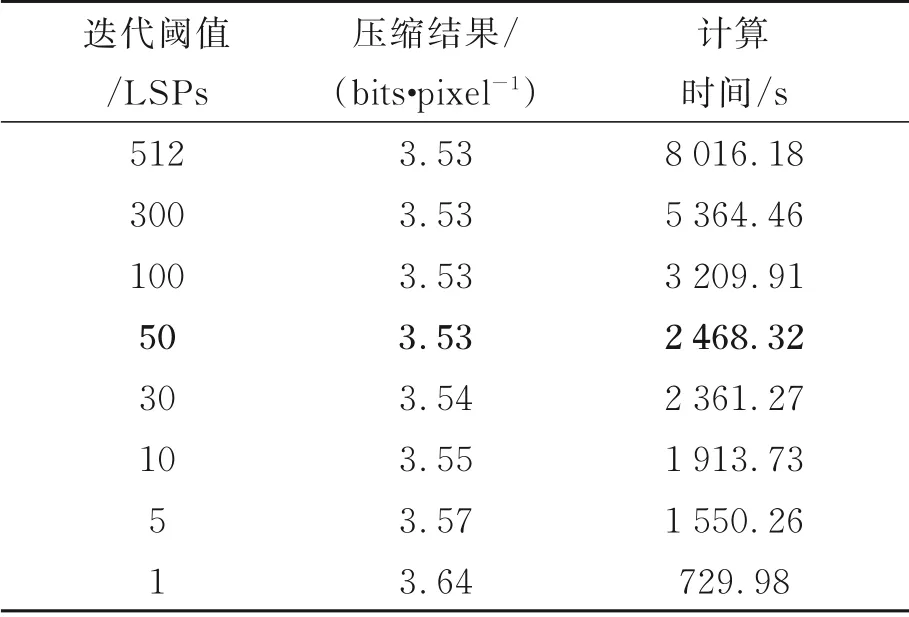
表2 不同参数下的压缩性能Tab.2 Compression performance under different pa⁃rameters
3.3 压缩性能的评估与分析
为衡量本文算法的压缩性能,将其与现有的 算 法(FL,IP3,RLS,ACRLS,and Fast-RLS-ALP)从压缩结果与计算时间两方面作对比。
表3展示各类算法的压缩结果。其中,ACRLS算法因采用穷举法查找每个波段的最佳预测长度,是已知同类型压缩结果最佳的压缩算法。本文提出的LFG-RLS算法采用格型滤波器组获取图像谱带的最优预测长度,并结合滤波器的收敛性,合理地选择迭代阈值,获取良好的压缩效果。在校准、未校准场景中的平均压缩结果分别是是3.34 bits/pixel和5.61 bits/pixel。该压缩效果与ACRLS非常接近,并优于其他压缩方案。此外,SLFG-RLS的压缩结果证实,当首个场景的预测长度应用于其他场景时,能获得相似的压缩效果。
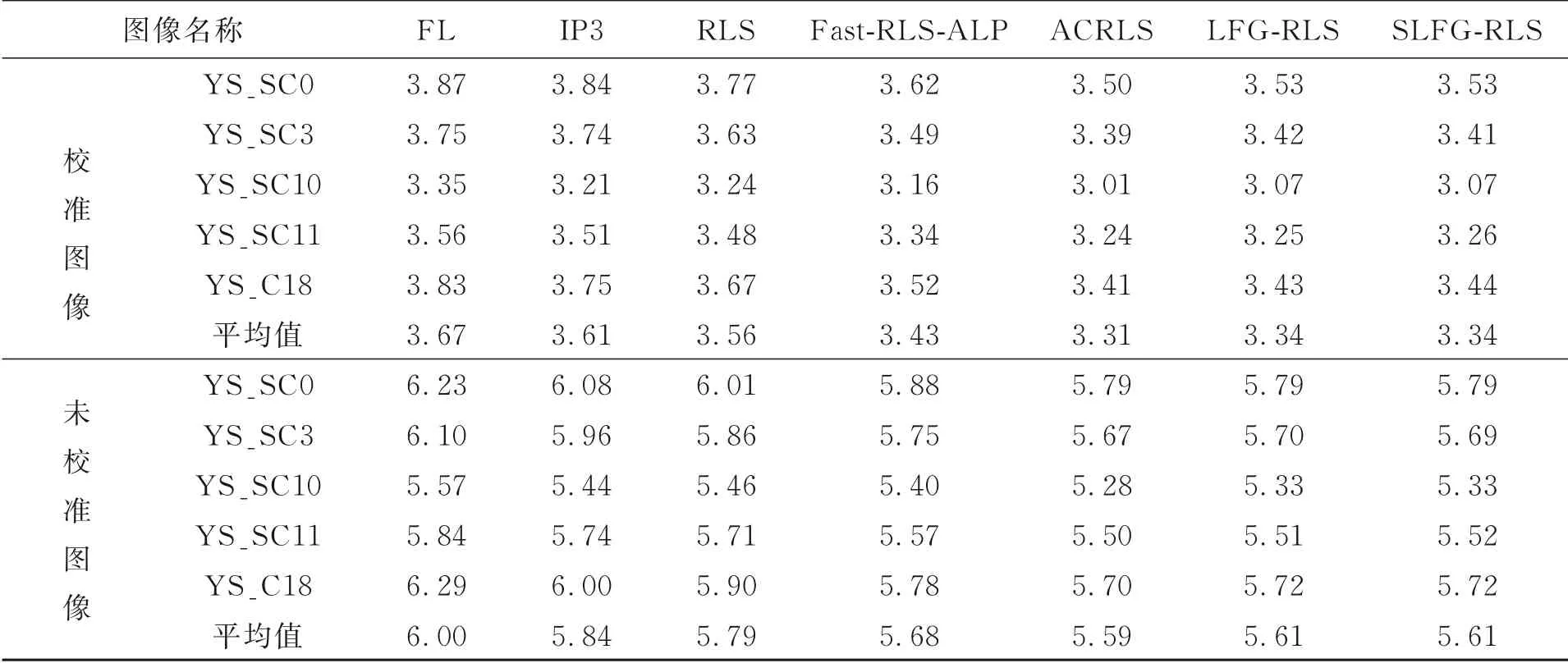
表3 不同算法的压缩结果Tab.3 Compression results of different algorithms (bits·pixel-1)
各算法的平均计算时间如表4所示,FL,IP3,RLS和Fast-RLS-ALP算法采用固定预测长度,预测方式较为简单,计算时间较短。ACRLS算法采用穷尽式的搜索方案计算所有待测点的最优预测长度,消耗较长的计算时间。

表4 各种算法的平均计算时间Tab.4 Average computation time of various algorithms (s)
本文提出的LFG-RLS算法,对于校准、未校准图像分别仅需1050 s,1064 s,相较于使用穷举法搜索最优谱带预测长度的ACRLS算法降低10余倍的运算时间。主要原因是本文合理地限定滤波器的迭代次数,并根据格型滤波器组链式更新的特点,对最优滤波器做分类与简化,大幅度减少待更新滤波器的数量,降低快速预测阶段的计算时间。
此外,谱带间预测器根据迭代阈值T可分为最优谱带搜索阶段和快速预测阶段,对于校准图像,LFG-RLS压缩方案两阶段平均耗时分别为767.8 s,262.9 s,最优谱带搜索阶段压缩的数据量约占总数据量的10%,但消耗总计算时间的73.1%。因此,若高光谱成像仪采集的图像尺寸越长或图像数量越多,最优谱带搜索阶段消耗计算时间所占比例越小,压缩方案所需总运算时间相对越短,能充分发挥算法的优越性。在SLFGRLS压缩方案中,系列校准、未校准图像分别是同一系统采集的多幅图像,将首个场景的预测结果推广后,对校准、未校准图像的平均计算时间分别降低至441 s和447 s。
为验证本文压缩算法的无损性,将压缩后的数据流做解压缩处理,得到恢复图像。将原始图像与恢复图像相比较,结果显示二者完全相同,表明高光谱图像信息没有任何损失。
4 结论
为充分挖掘高光谱图像的空间相关性和谱间相关性,本文提出利用格型递归最小二乘法滤波器组的高光谱图像无损压缩方案。该方案中充分考虑最优滤波器对预测效果的影响,采用格型滤波器组计算每个谱带的最优滤波器,并且根据其链式更新的特点,对筛选过程做进一步的分类与简化,大幅度降低压缩方案的计算复杂度。实验结果表明,以CCSDS提供的AVIRIS高光谱图像为测试数据集,本文的压缩方案具有良好的压缩性能,对16位校准图像、未校准图像分别取得3.34 bits/pixel和5.61 bits/pixel的压缩结果,与同类算法的最佳压缩结果相似,且其平均计算时间远低于其余具有相似压缩结果的算法,具有较强的竞争力,为高光谱图像无损压缩提供了一种有效的解决方案。未来将针对压缩方案的并行化处理做研究与探讨,并开发可行的硬件实现方案。
