PD Control with RBF Neural Network Compensation for Dynamic Positioning System

, , ,

(a.Key Laboratory of High Performance Ship Technology(Ministry of Education);b.School of Transportation,Wuhan University of Technology,Wuhan 430063,China)

Abstract:Dynamic positioning control system is influenced inevitably by external environment disturbances such as wind,wave and current in actual working conditions.This paper mainly studies the RBFneural network and PD control algorithm to improve the immunity and stability of a dynamic positioning system.RBF neural network is used to compensate for the environment disturbances,whose adaptability and robustness can be enhanced.The adaptive algorithm of weights is obtained by Lyapunov function analysis.Simulation comparison results of a supply ship confirm the effectiveness of the proposed controller.

Key words:dynamic position system;adaptive algorithm;RBF neural network;Lyapunov theory

0 Introduction

According to the International Maritime Organization(IMO)and other certifying class societies[1],a dynamically positioned(DP)vessel is defined as a vessel that accurately maintains its position and heading at the desired location or pre-determined track by means of a series of thrusters.DPSis widely used in plenty of operation vessels and platforms.In actual working conditions,uncertain hydrodynamic parameters and change of environment disturbances including wind,wave and ocean current make the control systema complex and nonlinear problem.

DPShas been applied on vessels since the 1960susing traditional proportional-integral-derivative(PID)control technique in combination with a low-pass and/or notch filter.Then the optimal control theory and Kalman filtering techniques were proposed and improved by Balchen et al[2-3]in the 1970s.The controllers of DP vessel were designed under the assumption that the kinematic equations can be linearized about 36 predefined constant heading angles,which results in that the parameter adjustment is complex and global stability cannot be guaranteed.In the 1990s,nonlinear control technique was presented in DP vessel control system,nonlinear output feedback control,backstepping observer and passive observer design were applied under the researches of Fossen[4],Grovlen[5]and Stranda[6].Until the end of last century,the intelligent control technique was developed,such as fuzzy method[7],robust control,neural network[8]and nonlinear model predictive control[9]etc..Fuzzy logic and neural networks have been put forward to deal with dynamic uncertain and nonlinear system because they do not need an accurate model of system.DPScontrol technology ismaking a progresson the intelligence.

Ship motions will be influenced by uncertain external environment forces during the movement of a vessel toward a target point.In the early stages of control,the PD controller forces a ship to move quickly to the target position.But there exists a weakness in PD control that the PD controller cannot guarantee the steady stage error to become zero because of the external environment disturbances.It is difficult for the PID controller to adjust the parameters to achieve good results and readjust the parameters when the experimental conditions change.Neural networks have the advantages of self-adaptation and self-learning to deal with nonlinear problems.A neural network and PD-combined controller was proposed in Ref.[10],the controller was composed of a RBF feedforward and a PD feedback.However,it lacked a global asymptotic stability proof.A PD controller with a RBF NN compensator was designed in this paper.The RBF NN compensator was used to compensate for the external time-varying environment interferences and its weight adaptive algorithm was obtained by Lyapunov function analysis.Ultimately,the global asymptotic stability of the hybrid controller was proved.

The main structure of the paper is organized as follows.In Chapter 1,a mathematic vessel model with uncertainties and disturbances is discussed,and RBF NN is introduced.Chapter 2 shows the design of the controller and the proof of global stability.The simulation studies illustrating the designed controller is presented in Chapter 3 and Chapter 4 contains some analysis and conclusionsof the paper.

1 Problem formulation

1.1 Mathematic model for DPvessel

For a DPvessel,the study of a mathematic model could be divided into two parts:kinematics,which treats only the geometrical aspects of motions,and kinetics,which is analysis of the forces causing the motion[11].In DPS,the control objective is regarded as 3 degree-of-freedom(DOF)problem in the horizontal plane in surge,sway and yaw.As shown in Fig.1,two coordinate frames will be used:the fixed coordinate frame and the body coordinate frame.OEXEYEis the earth-fixed coordinate frame called North-East-Down reference frame,which is fixed at a point of earth’s surface.OXYis the body coordinate frame,which is fixed to the vessel,and the coordinate origin is located at the gravity center of the vessel.

According to the theories of kinematics and kinetics,the nonlinear mathematic model of a sea-going vessel can be described asfollows:

Fig.1 Definition of two coordinate reference frames

whereη=[x yφ]Trepresents the position(x,y) and heading(φ)of the vessel in the earth-fixed coordinate frame,v=[u v r]Trepresents the surge velocity,sway velocity and yaw velocity of the vessel in the body coordinate frame.τ=[τ1τ2τ3]Trepresents the control forces and moment in the body coordinate frame.The vectorΔ(η,v) represents the uncertain structural perturbation and the unknown environmental forces and moment including the wind,wave and current.The earthfixed velocity vector is related to the body-fixed velocity through rotation matrixRwhich is orthogonal,that isR-1=RT.Mis the inertia matrix including the added inertia.C(v) is the Coriolis matrix andD(v) isthe damping matrix.These matrices are given as follows:

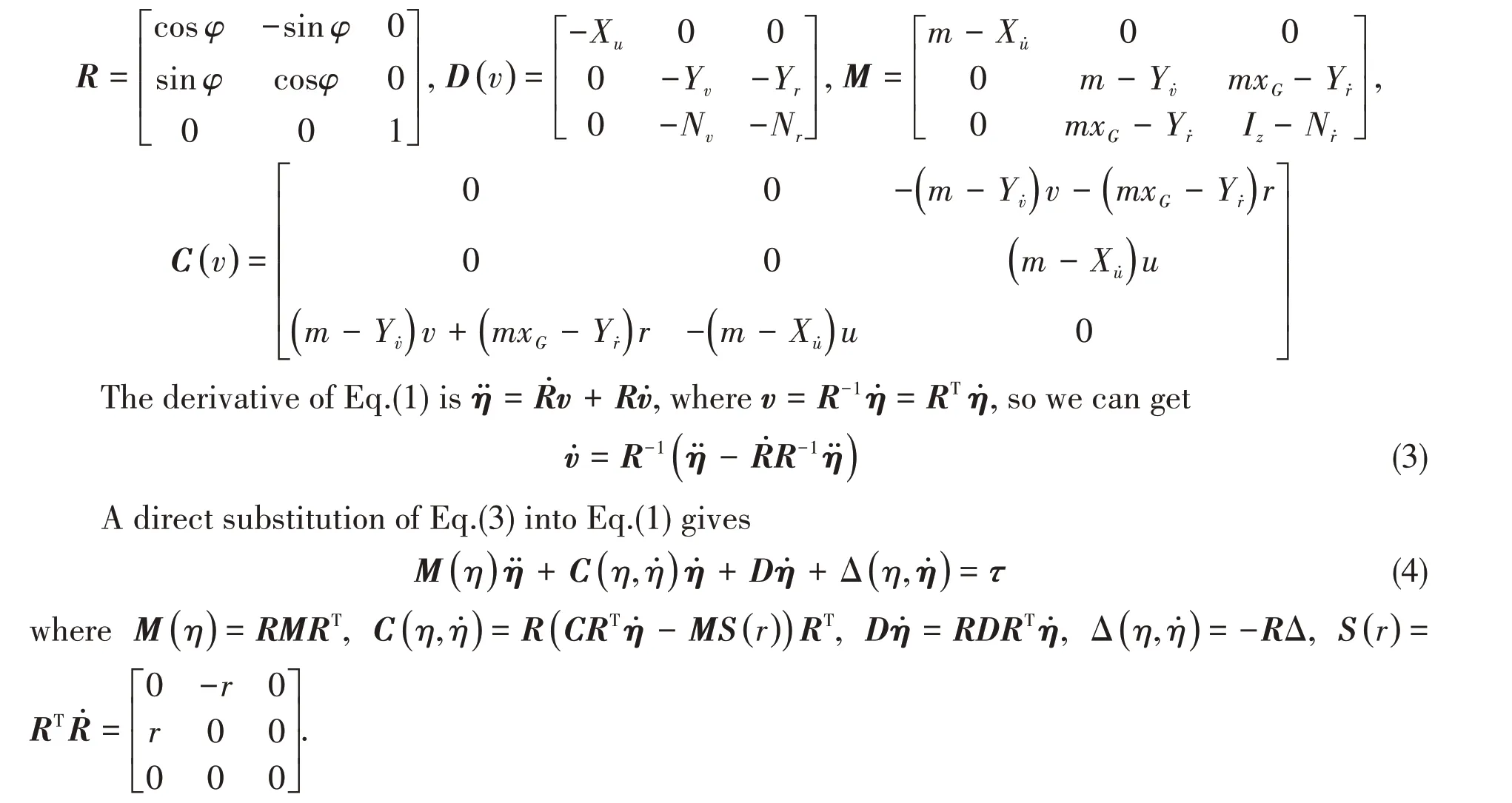
The DP vessel mathematic model has the following assumption and properties which will be used in the analysis of the controller.

Assumption 1:Both the positionη=[x yφ]Tand the velocityv=[u v r]Tmeasurements of DP vessel are available.

Property 1:The inertia matrix is symmetric and positive definite[12].

m1‖x‖2≤xTM x≤m2‖x‖2;∀x∈Rn

wherem1,m2are known positive scalar constant,and‖· ‖denotes the Euclidean vector norm.

Property 2:The centripetal and Coriolis matrix is skew-symmetric,which satisfies the following relationship:

1.2 Mathematic model for neural network

In the late 1980s,J.Moody and C.Darken proposed a RBF(Radial Basis Function)neural network,which is a three-layer feedforward network with a single hidden layer.The network can simulate the local adjustment of the human brain and cover the network structure of the receiving domain.Therefore,the network is also a local approximation network.It has proved that the network can approximate any continuous function with arbitrary precision.The specific network structure is shown in Fig.2[13].

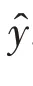
Fig.2 Structure of radial basis function neural network

whereX=[ ]x1,x2,…,xmis the input layer,εis the approximation error,whose magnitude depends on the valuesofW*andV*.

The RBF neural network is introduced to approximate and compensate for both unknown dynamics and disturbancesof ships as follows:

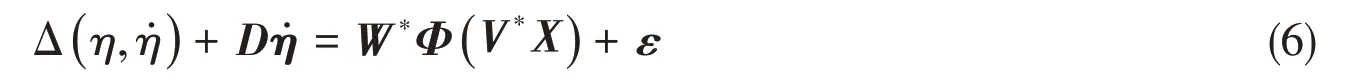
Since the ideal constant weight vectorW*andV*are‘artificial’quantities only for analytical purpose and cannot be gained,W^andV^are used to represent the estimation ofW*andV*.Property 3:It is clear that the Gaussian function,commonly used in RBF neural networks,satisfy Lipschitz condition.We may conclude that:

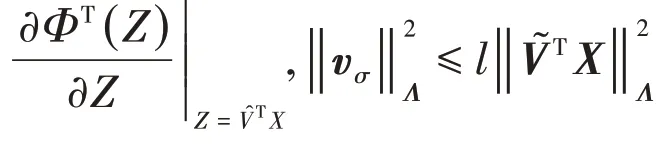
Assumption 2:For allx∈R,the ideal weight vectorsW*,V*and the approximationεare bounded,there exist positive constantsWM,VMandεM,which satisfyW*≤WM,V*≤VMandε≤εM.

2 Design of RBF NN controller for dynamic position

In this chapter,a PD controller with RBF neural network compensator is given and the adaption laws are designed by the Lyapunov stability analysis.We assume the velocities of the vessel are measurable and the PDcontrol ispresented asfollows:

whereηd∈R3isthe desired position andvd∈R3is the desired velocity of vessel,it isbounded as

KpandKdare positive defined matricescorresponding to proportional and derivative coefficients.

The tracking error is defined as:

The neural network can be trained online by the following adaption law:

where

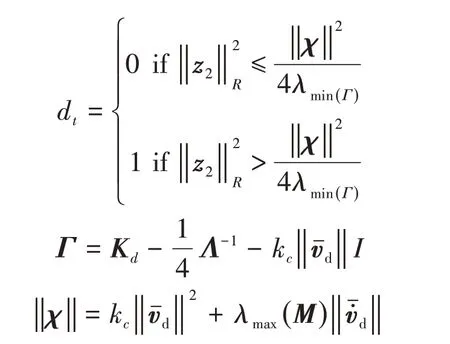
From Eq.(4)the closed-loop systemis

Let the Lyapunov function candidate be

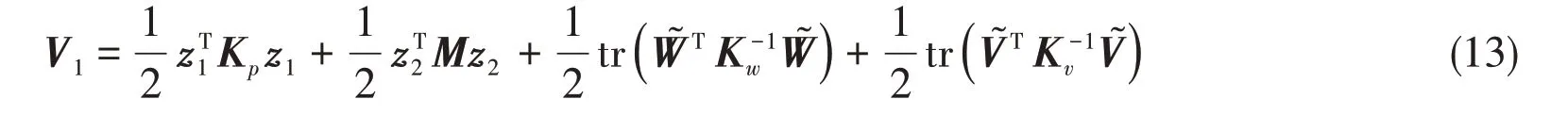
whereKwandKvare defined positive constant matrices.The derivative is

According to Eq.(12),

Then the time derivative ofV1becomes

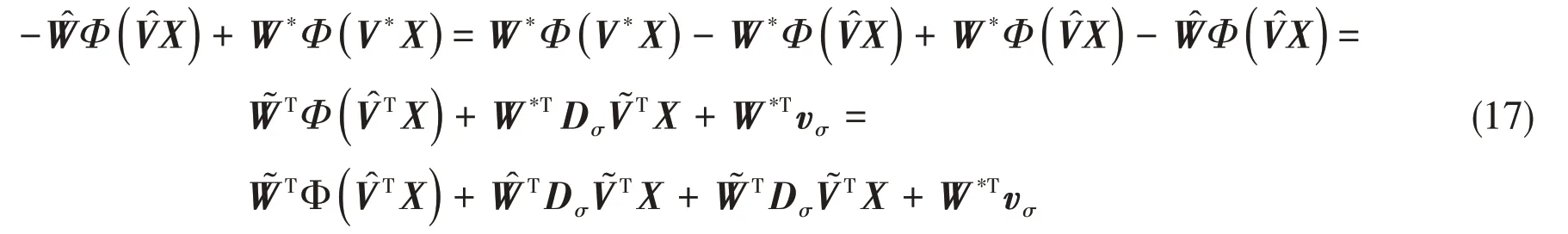
In view of inequality of the matrices,

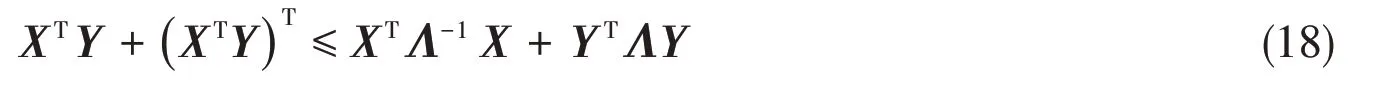
which is satisfied for anyX,Y∈Rand any positive defined matrixΛ.

Using Property 2,

Substituting Eq.(17)and Eqs.(19)-(21)into the Lyapunov function candidate,

where

The time derivative of Lyapunov function is negative if the gainΓ1is designed to satisfy the condition

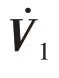
3 Simulation results

In this chapter,numerical simulations are preformed to verify the effectiveness of the proposed controller.The CybershipⅡin Ref.[14],which has two main propellers,two rudders aft and one bow thruster fore,was employed and the main hydrodynamic coefficients are tabulated in Tab.1.

In the simulations,the orientation position of the vessel isη=[ 0 m,0 m,0°]T,and then thevessel is required to move to the desired positionη=[ 10m,10m,5°]Tand maintain for a long time.The external environment disturbances including wind,wave and current will be added on the vessel during thewhole process.The environmental parametersin the simulation are shown in Tab.2.

Tab.1 Main parameters of vessel model

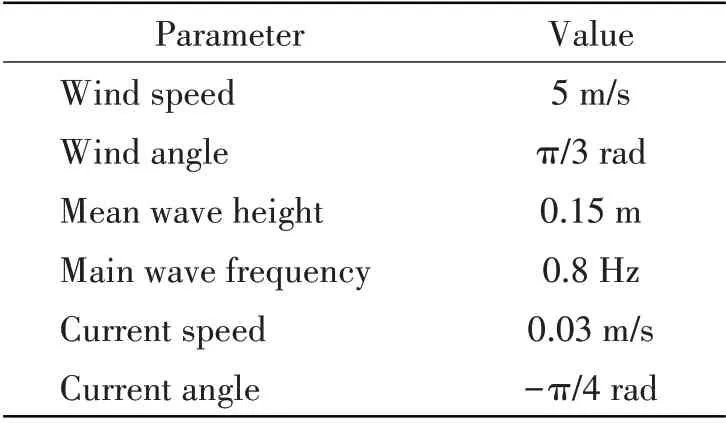
Tab.2 Environmental parameters

The simulation results depicted in Figs.3-5 show that the proposed controller is able to force the vessel to converge to the desired position more accurately than PID controller.The movements of the vessel are presented in Fig.6,which indicates that the actual vessel position can approach to the desired position[ ]10m,10m and maintain the position for a long time under the action of PD controller with RBF neural network compensator.However,the vessel arrives at a fixed position[10.8m,10.2m ]where errors always exist with the target position under the action of PID controller.The corresponding control forces and torque are shown in Fig.7.The fact that the curves of forces and torque are stable at a constant value shows that the controllerscan effectively adapt to the external environment disturbances.

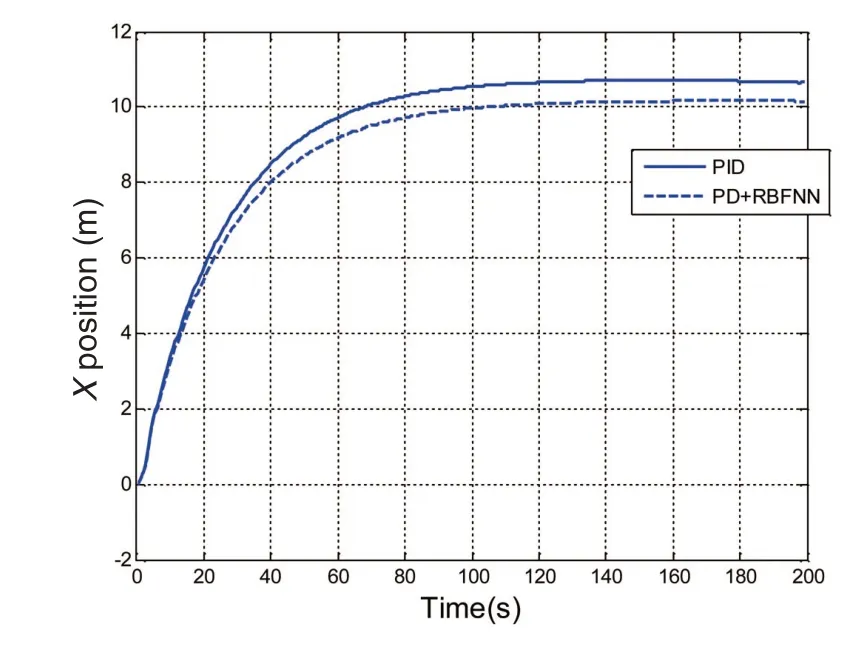
Fig.3 X position of vessel

Fig.4 Y position of vessel

Fig.5 Heading angle of vessel

Fig.6 Movement position of vessel

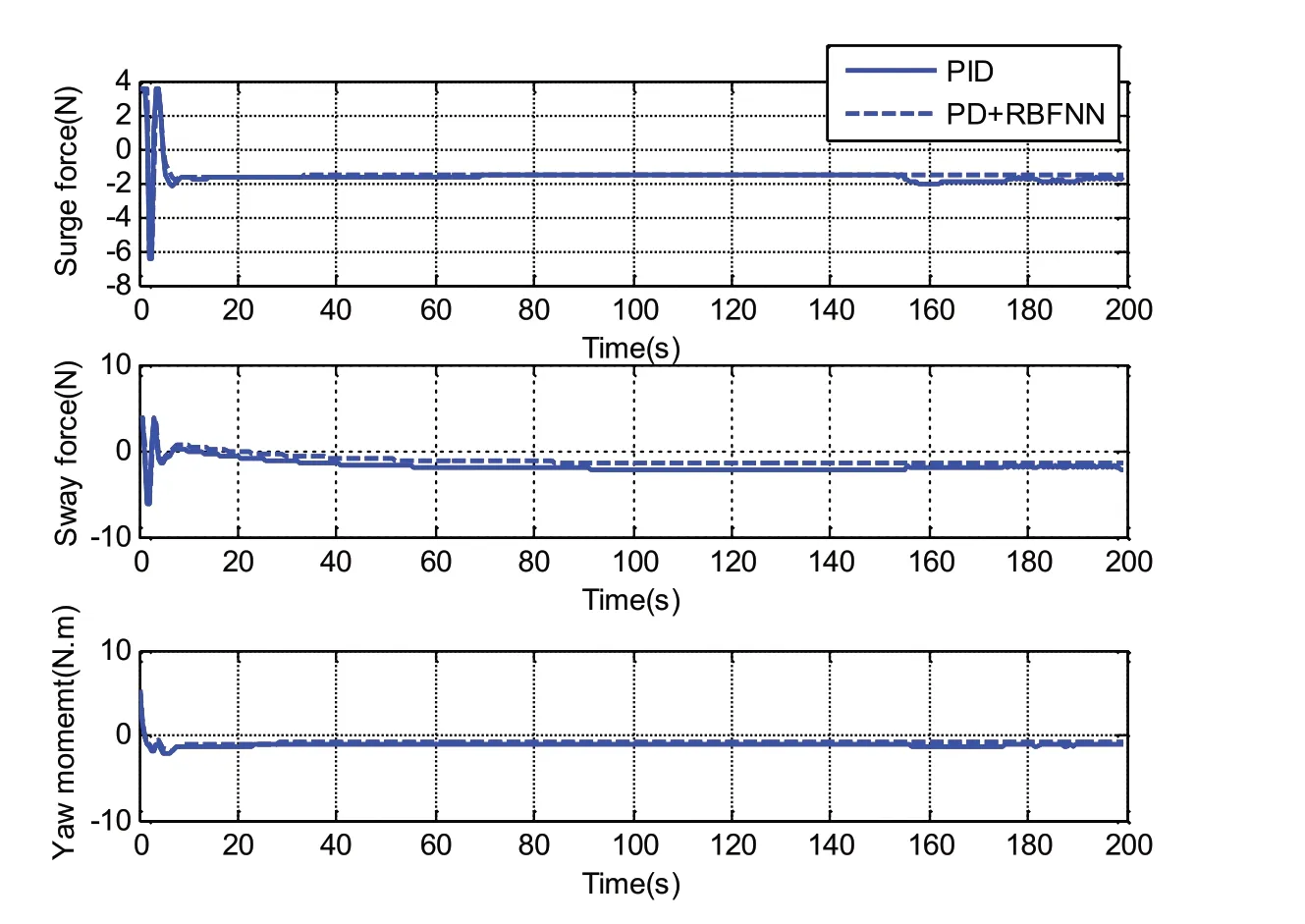
Fig.7 Control force and torque

4 Concluding remarks

In this paper,a PD controller with RBF neural network compensator was proposed to deal with external environment disturbances such as wind,wave and current.The RBFneural network was introduced to replace the integral term because of its strong adaptive ability.Then the weight adaptive law of the neural network was given.Global asymptotic stability of the proposed controller was proven by means of Lyapunov stability theory.Simulation results show that the proposed controller is able to compensate for external environment disturbances.Comparison with PID controller confirmed the effectivenessof proposed approach.