Application of the Cell-vertex Finite Volume Method in the Solution of the Lubrication Characteristicsof Journal Bearings

,,,

(1.College of Power and Energy Engineering,Harbin Engineering University,Harbin 150001,China;2.China Ship Development and Design Center,Wuhan 430064,China)

Abstract:The cell-vertex finite volume method is presented to solve the transient Reynolds equation in this paper.The discretization of the Reynolds equation is based on the vectorization method and the lubrication region was meshed with unstructured grids,thus,this method can guarantee the conservation of lubricant film in the clearance and has good adaptation in the regions with complex shape.The adaptation and accuracy of the presented algorithm are validated by some bearing models.The results show a good agreement with the reference values.According to the calculated pressure distribution,the number and types of the grids in the lubricated area are readjusted and the calculation time is compared as well.The pressure distribution of the journal bearing with circular cone textures is calculated and the results show that the pressure value on the circular boundary can be shown clearer when the unstructured grids are applied.

Key words:cell-vertex finite volume method;transient Reynolds equation;unstructured grids;journal bearing;lubrication characteristics

0 Introduction

Journal bearings are widely used in the field of mechanical engineering.When the journal centre runs on the eccentricity position,the convergent clearance will be formed by the lubricant between two surfaces,and the bearing external load will be balanced by the fluid film pressure[1],as a result,the surfaces of the journal and bearing bush will be separated,and the friction loss will be reduced.

The Reynolds equation is an important equation in the solution of the fluid film pressure.Except for the one-dimensional Reynolds equations of the infinite short and long journal bearings that can be solved by the analytic methods,the two-dimensional Reynolds equation of the finite long journal bearings can only be solved by numerical simulation methods,such as the finite difference method(FDM),the finite element method(FEM)and the finite volume method(FVM).

The FDM is the most common numerical method in the calculation of the Reynolds equation.The gradient term can be obtained by Taylor expansion.Some researchers have done numerous studies with this method.Sun et al[2-3]studied the influences of the misalignment state and shaft deformation on the lubrication characteristics.Wang et al[4-5]studied the transient lubricating performance of the journal bearing lubricated with non-Newtonian fluid.He et al[6]investigated the mixlubrication characteristics of a stern bearing considering the cavitation and shaft deformation.Cheng and Ji[7]studied the slip effects in the journal bearing.But the lubrication region can only be meshed with structured grids,which is shown in Fig.1(a).But it is hard for the FDM to calculate the pressure distribution of journal bearings with a complex shape.

The FEM also has some applications in the solution of Reynolds equation.Based on the variational principle,the Reynolds equation will be written as the functional equation.This algorithm has a strong adaptation to the complex region,as shown in Fig.1(b),thus,the grid size and node number can be selected freely.These advantages of FEM ensure this method can also be used in the lubrication field[1].Some researchers have done the related investigations.Willis et al[8]investigated the EHD lubrication phenomenon.Mourelatos[9]studied the lubrication characteristics of engine crankshafts.Liu et al[10]studied the mixed elasto-hydrodynamic lubrication of journal bearings systems.Fatu et al[11]studied the thermal elasto-hydrodynamic lubrication performance of journal bearings.Durany et al[12-13]studied the thermo-hydrodynamic lubrication,and in the two literatures,the one and two-dimensional Reynolds equations were computed separately.But as pointed out by Profito[14],the FEM has the limitation of guaranteeing the flow conservation on the arbitrary cavitation boundary.

The finite volume method(FVM)has the property of strong conservation.This method also has some applications in the calculation of Reynolds equation.Arghir et al[15]solved the Reynolds equation with the FVM and the quadrilateral meshes in the research of film discontinuities,and the coordinate transformation[16]was used for the purpose of aligning the grid lines.Arghir et al[17]calculated the Reynolds equation using the classical FVM(cell-centered style)and triangular meshes in the study of the non-linear analysis of gas bearing.The gas pressure variable is defined on the cell center and the pressure of the nodes is the arithmetic mean of the neighboring cell centers.Profito[14]applied the general FVM in the calculation of the general Reynolds equation,the solution of equations was based on the Gauss-Seidel method with successive over relaxation.As is shown in Fig.1(c),the pressure variable is defined on the nodes and the control volume is constructed by the sub-regions of the neighbouring elements.The cell-vertex finite volume method(CVFVM,used in this paper)has a good adaptation in the lubricating areas with irregular shape,the pressure variable is defined on the nodes as well,which is similar to the general FVM[14].The differences of the two algorithms are reflected in the treatment of the time term and the calculation method of equations.However,CVFVM has been applied less in the solution of Reynolds equation specifically corresponding to the journal bearings.

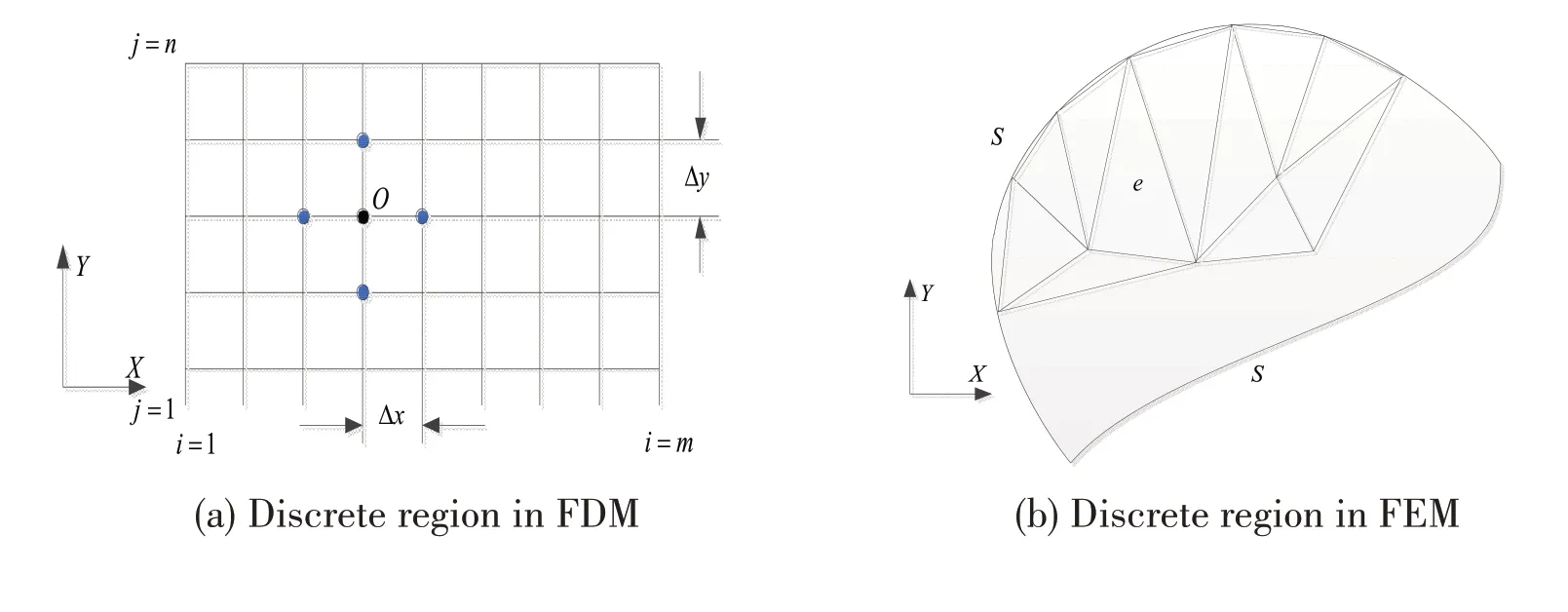
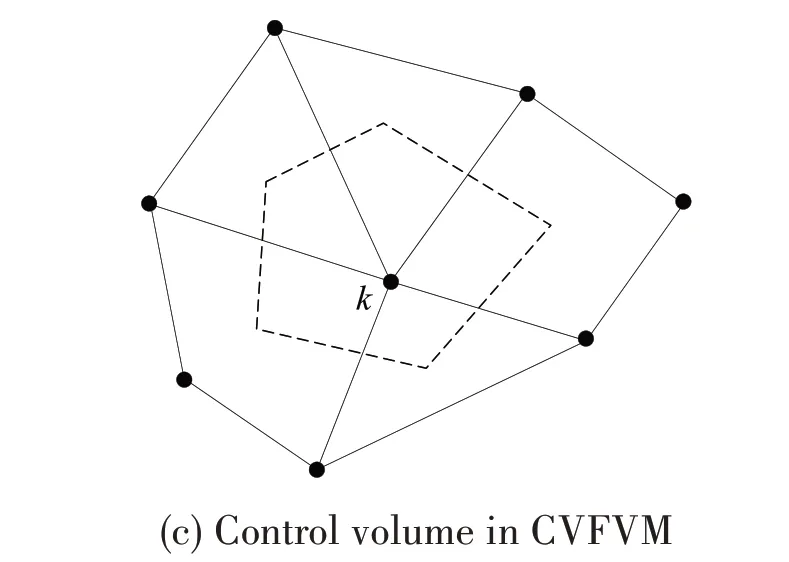
Fig.1 Discretization of the lubrication region

It should be emphasized here that the main purpose of this paper is to apply the CVFVM in the study of the lubrication characteristics of the journal bearings with complex shape rather than the comparison between the current numerical method and other algorithms.The main innovation point is the solution of the Reynolds equation specifically corresponding to the journal bearings based on the CVFVM and unstructured grid technology.The calculation of discrete algebraic equations is based on the multi-grid method.The axis orbit will be calculated by the equation of journal motion equation.

This paper will be divided into five parts:(1)the Reynolds equation and the related formulas for calculating the lubrication characteristics are presented;(2)the Reynolds equation is discretized using the vectorization method to allow it to be used in the irregular region;(3)some test cases are computed by using the CVFVM,and the adaptation,accuracy and effectiveness of current algorithm are discussed;(4)the calculation time of the models with different local refining are compared;and(5)the CVFVM is used to calculate the pressure results of a journal bearing with circular cone textures.

1 Theory analysis

The basic formulas for investigating the lubrication performance of journal bearings are presented in this chapter.Fig.2 indicates the geometric structure of a journal bearing and the force condition of the journal.

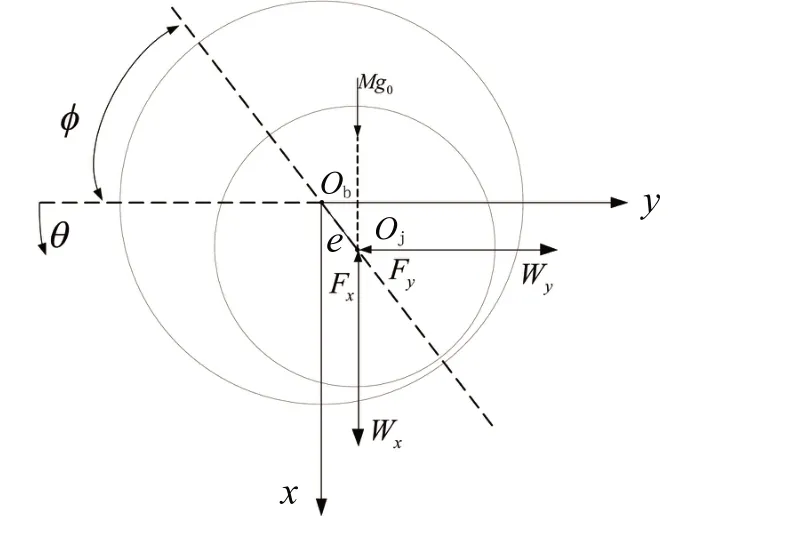
Fig.2 Journal bearing model considering dynamic load

1.1 Reynolds equation

The fluid film pressure in the journal bearings can be obtained by solving the two-dimensional transient Reynoldsequation[1]:

whereθis the angular coordinate,his the film thickness which is determined by the geometric clearance between two surfaces,pstands for the film pressure,Ris the bearing radius,zis the width coordinate of the bearing,Uis the journal speed,μis the lubricant viscosity,andtis time.

For the convenience of derivation and analysis,the non-dimensionalized form of Eq.(1)can be obtained by adopting the following formula:

Thus,the dimensionless Reynolds equation can be written as

The Reynoldsboundary condition is often used to calculate Eq.(3):

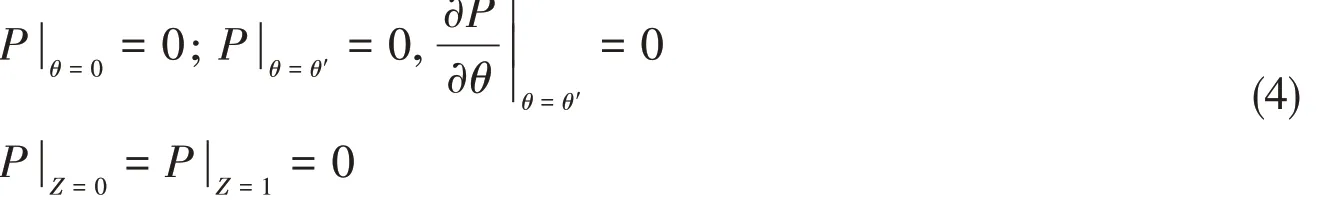
whereθ′is the undetermined film rupture boundary,andZis the dimensionless width coordinate of the journal bearing,HandPare the dimensionless film thickness and pressure,τis the dimensionless time.

For the purpose of studying the cavitation phenomenon[18]existing in the journal bearing,Eq.(3)will be transformed into the following:

where

andgis the switch function,λis the non-dimensional pressure in the full film region and the density ratio minus 1 in the cavitation region.ρcis the equivalent density of lubricant film in the cavitation region,and the film pressure is equal to thePcav,which is the cavitation pressure.

The boundary conditions of mass conservation cavitation theory[6,19-20]will be selected in the solution of Eq.(5):

To adapt the unstructured grid,Eq.(5)can also be given in the following vector form:

where

1.2 Film thicknessequation

The coordinate(x,y) is defined as the coordinate of the journal centre,thus,the film thickness of the journal bearing can be expressed by:

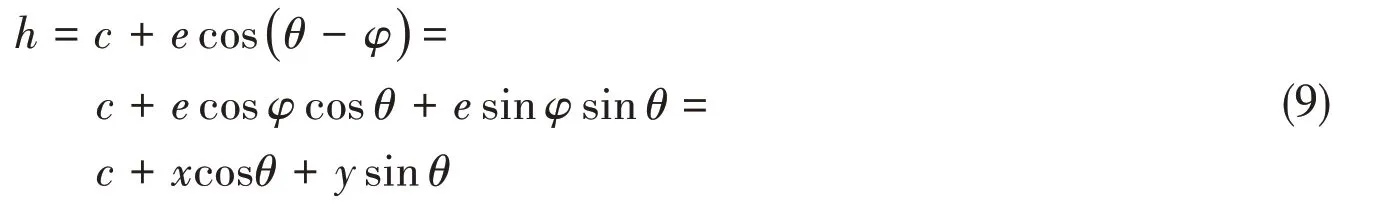
wherecstands for the radial clearance,eisthe eccentricity,andφisthe attitude angle.

The dimensionlessformof the film thickness can be written as

where

The gradient of the film thickness with respect to angle and time can be expressed as

Thus the source term can be rewritten as

The time term is implicitly integrated[17]as

It should be noticed here that only the first term in the right hand exists in the full film region,and the second term exists in the cavitation region.

1.3 Fluid film force

The fluid film force along thexandydirectionscan be obtained by

The total fluid filmforceFcan be obtained by

1.4 Equation of motion

According to the Newton’s second law,the motion equation of the journal centre can be expressed as

2 Discretization of the Reynolds equation

The integration of Eq.(8)in the control volume isexpressed as follows:

According to the Gauss divergence theorem,the diffusion term can be transformed to the following form:

wherencdenotes the total number of elements around Nodek.ncniis the total number of nodes of element numberedi,n⇀denotes normal vector of the control body boundary,Sis the integration line around the control volume,γdenotesxcoordinate andycoordinate,Nijis the shape function,Γiis the diffusion coefficient.See Ref.[21]for more information regarding the integration of the derivatives of the shape function.

Assuming that the source term and time term are evenly distributed,the integration of the two terms can be expressed as

Finally,Eq.(18)can be transformed as

The general form of equation can be written as

where

wherencni-1 indicatesthe remaining nodesin the cell numberediexcept for Nodek.

The algebraic multi-grid method can accelerate the iterative convergence rate of the algebraic equations derived from the elliptic equations[22-23],thus,the method is used to calculate equation.

3 Analysis of validation models

To prove the adaption,accuracy and efficiency in the solution of the Reynolds equation based on CVFVM,three test cases are chosen here for the verification analysis.The first model is the journal bearing with misalignment[2],the second model is the journal bearing with cavitation[6,19],and the third model is for the transient analysis of the journal bearing[24].The codes are programmed in Fortran 95 and run in a computer with 4 GBRAMand Intel Core i5-2400 CPU 3.1 GHz.

3.1 Misalignment journal bearing

In the actual working condition,shafting misalignment will occur because of the mechanical load and thermal load.The tilt angles are used to describe the misalignment situation in the current model which is used to test the adaption and accuracy of the CVFVM in the solution of the Reynoldsequation.The bearing parametersand the lubricant viscosity are listed in Tab.1.

Tab.1 Geometric and operational parameters

The pressure curves in Fig.3 are extracted from the exact locations at 0.033 m,0.050 6 m,0.059 4 m and 0.063 8 m separately along the width direction of bearing,these locations are the positions of the peak pressure under different slope angles.Fig.3 shows that the pressure results agree well with the reference values.

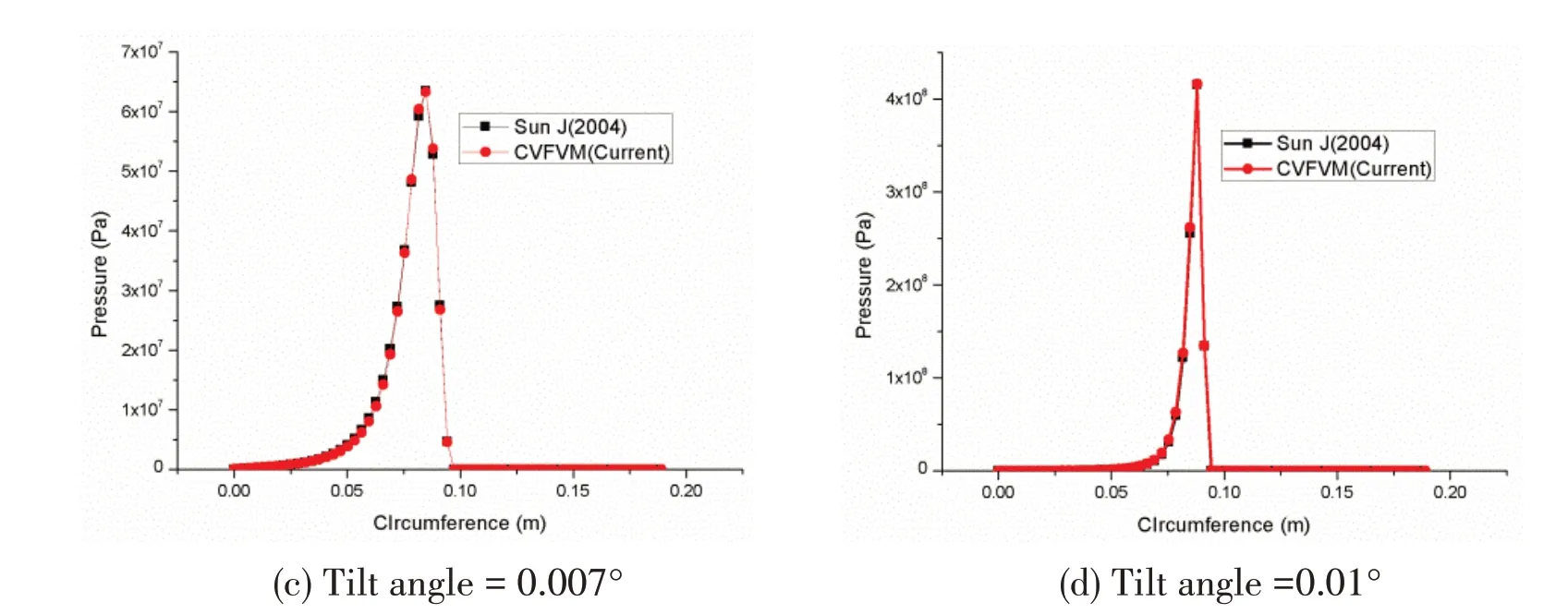
Fig.3 Comparison of the pressure distribution under different tilt angles

3.2 Comparison of the film pressure in the journal bearing with cavitation

In this model,the capability of CVFVM in the calculation of the cavitation phenomenon will be tested.The mass conservation boundary condition in equation will be used here.The calculation parameters are listed in Tab.2.The pressure distributions in two different sections are compared with the simulation results of He[6]and the experiment results of Jakobsson[19].As shown in Fig.4,the film pressure tendency of CVFVM is in agreement with the reference value,and it is closer to the experiment result in the range of 270°～360°.

Tab.2 Parametersfor the cavitation model

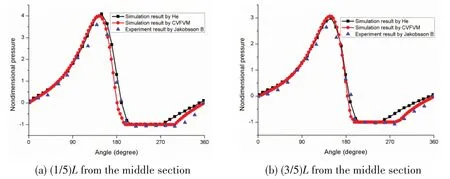
Fig.4 Comparison of the film pressure along different sections

3.3 Validation of the transient lubrication performance

For the validation of the calculation efficiency for the transient Reynolds equation by CVFVM,the model in Ref.[24]will be solved here.The bearing parameters are listed in Tab.3.The flowchart is shown in Fig.5.It should be emphasized that the initial position of the shaft center has no effects on the final convergence position.

Tab.3 Bearing parameters for the dynamic calculation

Fig.6 reveals that the journal position fluctuates in the previous period of time and eventually becomes stable at a certain position.The stable position is(0.109 5,0.300 7),which is very close to the reference value of(0.117 9,0.301).The film force is(-0.475 5,-2.225E6),which is in accordance with the reference value.In addition,the time loss is 0.18 hours,which is lower than 12 hours required in reference[23],the advancement of efficiency can be attributable to the superiority of Fortran compiling environment,the improvement of computer performance,and most importantly,the application of the algebraic multi-grid method.

Fig.5 Flowchart for the dynamic calculation

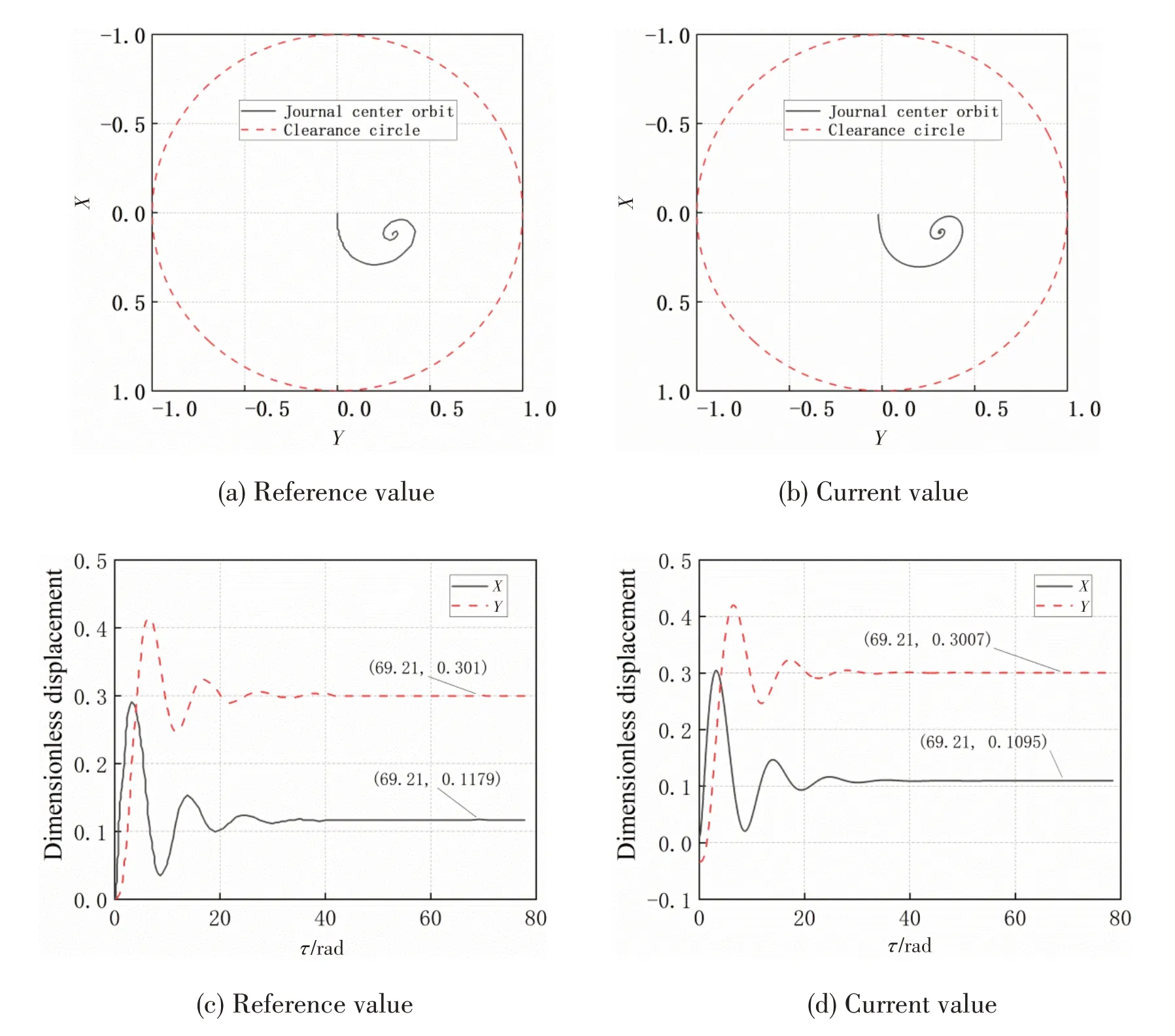
Fig.6 Comparison of the transient results

4 Effects of grid local refining on the calculation time

According to the strong conservation of CVFVM,the lubrication region could be meshed into grids of different densities while guaranteeing the accuracy.So the influence of grid local refining on the calculation time will be investigated in this chapter.The bearing parameters listed in Tab.1 are used here.The dense grid will be used for the region where the pressure is higher,whereas the sparse grid will be applied for the region where the pressure is near zero.For the current model,the pressure of the region from 0.1 m to 0.188 5 m is close to zero.As a result,this part will be meshed with sparse grids.In this part,nine cases will be solved to certify the superiority of CVFVM in the improvement of efficiency.The pressure results are shown in Fig.7,and the grid type,node number,element number and calculation time are listed in Tab.4.The pressure distributions are nearly same,and the width of high pressure region isfrom 0.05 m to 0.1 m.The results show a good adaptation and accuracy of CVFVM in different typesof grids.

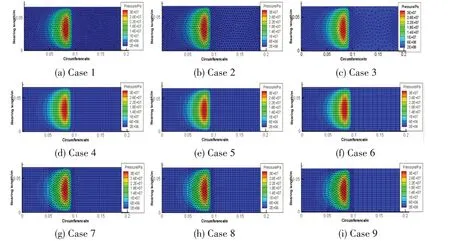
Fig.7 Fluid film pressure distribution with different grids

Tab.4 Basic parameters for the validation cases

Tab.4 also reveals that the calculation time decreases with the decrease of the node number.This technology can be used in the calculation of bearings with more complex calculation domain,and the computational efficiency will be improved.

5 Analysis of the textured journal bearing

The surface texture has the ability of reducing the friction and improving the lubrication performance.Thus,this technology hasbeen used in journal bearings[25].

To reflect the advantages of the flexibility of the current algorithm in a complex region,the pressure distribution of the journal bearing with circular cone textures is studied in this chapter.Because of the variation of film thickness in the local region of the texture,film discontinuities and first-order pressure derivatives discontinuities often occur[14].As a result,the unstructured grids are used in the vicinity of the texture boundary.The purpose of this model is to illustrate the advantages of CVFVM in the complex region rather than the study of discontinuities.

The relevant parameters are listed in Tab.5 while the detailed geometry features are shown in Fig.8.The surface is divided into three parts.The textured region has 400 texture cells,with 10 texture cells along the circumferential direction and 20 texture cells along the bearing width direction.The mesh schemes are shown in Fig.9 and the pressure resultsare shown in Fig.10.

As shown in Fig.10,the pressure distributions in the whole bearing surface are basically the same.However,a clearer description of the pressure is found at the texture circular boundary when the irregular grids are used.This advantage is helpful for the study of the discontinuities near the irregular texture.

Tab.5 Parameters of the journal bearing with circular cone textures

Fig.8 Texture distribution in the bearing surface

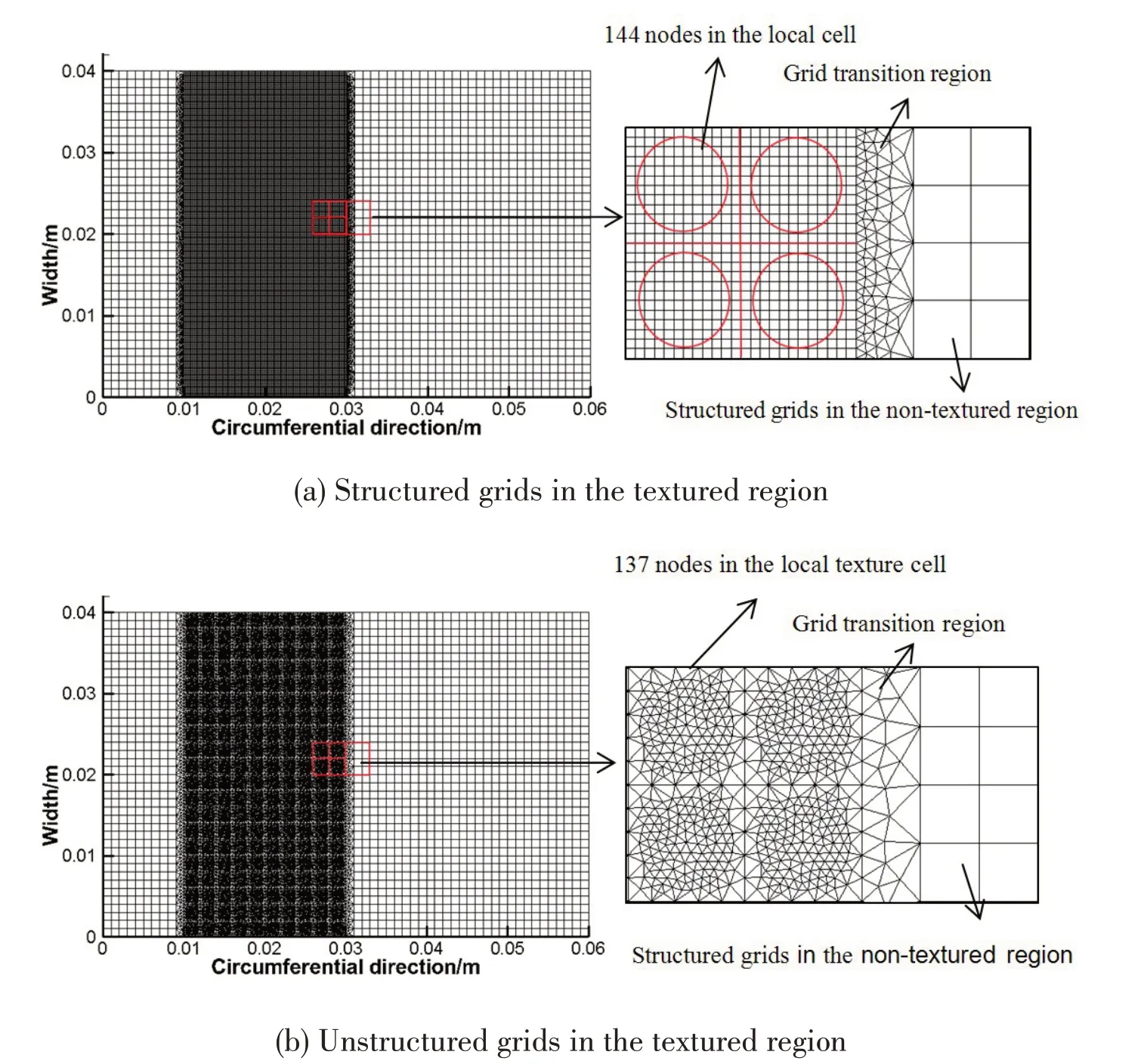
Fig.9 Comparison of two mesh schemes

Fig.10 Comparison of the pressure distribution

6 Conclusions

An algorithm based on CVFVM for the calculation of the transient Reynolds equation is presented in this paper.The transient lubrication characteristics of the journal bearings are analysed.According to the comparison and analysis results,the main conclusionsare drawn as follows:

(1)CVFVM is applicable for the solution of the 2D Reynolds equation.The test results of two models considering misalignment and cavitation reveal that the pressure distribution agrees well with the simulation and experiment results.

(2)According to the calculations of the lubrication region meshed with triangular grids,quadrilateral grids and mixed grids,the accuracy of the results is good.Thus,the adaptation and accuracy of the unstructured gridsis acceptable.

(3)As the results of the current CVFVM in the transient Reynolds equation show good agreement with the reference results,the CVFVM can be used to study the transient problems.Moreover,the efficiency of the current algorithm is higher than the reference value,so the algebraic multigrid method isan alternative way to decrease the calculation time.

(4)The results of the circular cone textured-bearing illustrate that the CVFVM is an effective method to study the pressure results of the complex texture boundary and assist the study of complex shape bearings.

Acknowledgements

This work is supported by the National Natural Science Foundation of China(50909023)and the program of research on the key technologies of measurement and design assessment of ship underwater radiated noise.