基于广义主成分分析的图像重建

张雪纯，廖 亮，魏平俊

(中原工学院 电子信息学院，河南 郑州 450007)

基于数据降维的特征提取和数据分析长期以来在机器学习和计算机视觉任务中扮演着十分重要的角色[1]。主成分分析(principal component analysis，PCA)是常用的特征提取方法之一。主成分分析算法在提取数据特征时需要对原始数据进行向量化处理，然而简单的图像数据向量化往往会导致图像像素邻域约束的丢失。杨健等[2]提出了针对图像的二维主成分分析(two-dimensional PCA，2DPCA)算法，并将其运用于人脸数据集的识别中，较经典PCA算法、2DPCA算法有更好的性能。在2DPCA算法的基础上，张道强等[3]提出了双向二维主成分分析(two-directional two-dimensional PCA，2D2PCA)算法，该算法可同时提取来自图像行和列方向上的特征用于人脸数据集的识别，也取得了较好的效果。Chen等[4]提出了矩阵模式主分量分析(MatPCA)算法，这是一种针对图像的直接对矩阵进行特征提取的方法。此外，Wang等[5]提出了一种从给定数据中估计结构子空间的张量列主成分分析(tensor train PCA，TT-PCA)算法，该算法保留了数据的低秩张量结构，对噪声具有鲁棒性，在公有图像数据集上也验证了有效性。上述基于主成分的算法虽在一定程度上提高了经典PCA算法的性能，但均未涉及像素空间约束信息。为了进一步优化PCA算法，提高图像特征提取及图像重建的质量，本研究将PCA算法推广为广义主成分分析(tensorial principal component analysis，TPCA)算法[6-7]，并使用TPCA算法对MNIST图像集进行特征提取和图像重建，以给出广义算法和经典算法的定量比较。

1 相关算法描述

对传统PCA算法、广义矩阵代数中的部分符号约定与基于广义矩阵代数的TPCA算法的相关数学描述进行介绍。

1.1 PCA算法

PCA是一种经典的数据分析算法，常用于图像特征提取及重建。由于图像数据的冗余性，原始图像信息通常可以通过正交变换映射到一个低维子空间上，从而达到提取原始图像主要特征和压缩信息的目的。经典PCA算法可以借助矩阵的奇异值分解(singular value decomposition，SVD)来完成，具体步骤可以归纳如下：

设训练集由K个向量x1，x2，…，xK∈D构成，并记训练向量的平均值为

(1)

则训练向量x1，x2，…，xK的协方差矩阵可由下式得出：

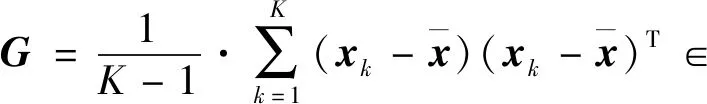
(2)

式中：G为对称矩阵，即G=GT。矩阵G的奇异值分解由下式给出：

G=U·S·UT，

(3)

式中：U∈D×D为正交矩阵，满足UT·U=U·UT=I(I为单位阵)；S=diag(λ1，…，λD)∈D×D为对角矩阵，λ1，…，λD为奇异值。

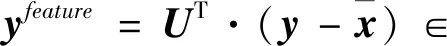
(4)

如果要将向量yfeature∈D由D维降至d维，仅需要将向量yfeature的最后D-d个元素舍弃即可。

用特征向量yfeature和正交矩阵U重建向量yfeature∈D，可以由以下公式得到：

(5)

式中：(U)：，1：d∈D×d为保留矩阵U的前d列子矩阵；(yfeature)1：d∈d为保留向量yfeature前d个元素的子向量。

1.2 TPCA算法

广义矩阵代数将由标量作为元素的向量，矩阵扩展为由广义标量作为元素的广义向量、广义矩阵，而广义标量的集合在循环卷积下形成代数环C，TPCA在广义矩阵代数的基础上扩展了基于矩阵代数的PCA。文献[7]将广义标量命名为“t-scalar”，本研究后续描述将沿用文献[7]中的符号约定。表1为广义矩阵代数的一些基本符号及其解释。

表1 广义矩阵代数的部分符号及其解释Tab.1 Some symbols and explanations of T-algebra

表1(续)

假设一组来自训练集的广义向量XTV，1，XTV，2，XTV，3，…，XTV，K∈CD(K为训练集中广义列向量的个数，D为广义向量中广义标量的个数)。它们的广义协方差矩阵可依照式(6)计算得出，式(6)如下：

(6)

(7)

式中：UTM,VTM∈CD×D≡I1×…×IN×D×D为广义正交矩阵且满足为广义单位矩阵；STM=diag(λT,1,…,λT,D)∈CD×D为广义对角阵，λT,1,…,λT,D为广义特征值。

(8)

(9)

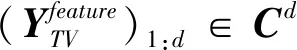
值得注意的是，若广义标量为0阶数组，即I1=…=IN=1，广义标量退化为标量，广义矩阵退化为经典矩阵，TPCA退化为经典PCA算法。

2 基于TPCA的图像重建

传统的PCA算法忽略了图像中各像素之间的联系，丢失了空间约束信息，针对传统方法对像素空间约束信息描述的先天不足，本研究使用文献[6-7]所描述的像素邻域方法将各个像素扩展为复合像素形式的广义标量。具体地，可以将图像中各像素周围的邻域像素作为一个尺寸为3×3的2阶数组，即广义标量，而以广义标量作为复合像素的原灰度图像随之扩展为广义矩阵。事实上，广义标量可以为任意尺寸和阶数的数组，若进一步扩展广义标量的阶数，可以在现有范围内邻域像素的基础上，取每个邻域像素周围的邻域像素，从而得到一个大小为3×3×3×3的4阶广义标量。同理，广义标量可以继续被扩展为大小为3×3×3×3×3×3的6阶数组。对图像像素具体邻域的扩展如图1所示。在图1中，原始像素由一个标量构成，该原始像素周围的方框区域所包含的邻域像素构成2阶数组形式的广义标量，而方框2区域的像素是由方框1区域的第一个像素再次邻域扩展得到的，若对方框1区域内的每个像素邻域扩展，即可得到4阶数组形式的广义标量。按照这种方法，原始像素的邻域可以扩展为任意阶数的广义标量。特别地，若所选取的像素邻域范围超出原始图像，则由0填充。

图1 手写数字图像“8”的像素邻域扩展方法Fig.1 The pixel neighborhood extension method of handwritten digital image "8"

通过对像素的邻域扩展，使得图像可以保留一定范围内的空间约束信息，此时运用TPCA完成对该广义图像的重建。具体步骤如下：

(1)图像预处理

①假设训练集与测试集中的每幅图像分辨率为D1×D2=D，其中训练集包含K个图像Xk∈D1×D2，1≤k≤K，测试集图像为Y∈D1×D2。将图像中像素扩展为I1×I2大小的2阶广义标量，使得图像转化为广义矩阵XTM，k∈CD1×D2≡I1×I2×D1×D2，1≤k≤K，YTM∈CD1×D2≡I1×I2×D1×D2。

②将广义矩阵XTM，k∈CD1×D2≡I1×I2×D1×D2，1≤k≤K，YTM∈CD1×D2≡I1×I2×D1×D2向量化，得到广义向量XTV，k∈CD≡I1×I2×D，1≤k≤K，YTV∈CD≡I1×I2×D。

(2) 在空间域中广义向量或广义矩阵的循环卷积和共轭转置等运算可以转换为傅里叶域中若干个向量或矩阵彼此独立的线性运算[6-8]。借助傅里叶变换对TPCA进行快速运算：

①将XTV，k∈CD，1≤k≤K，YTV∈CD傅里叶变换为广义向量XFTV，k∈CD，1≤k≤K，YFTV∈CD，则XFTV，k∈CD，1≤k≤K，YFTV∈CD可以各自分解为I1×I2个切片：传统向量XFTV，k(i1，i2，：)∈D，1≤k≤K，YFTV(i1，i2，：)∈D。

②利用切片XFTV，k(i1，i2，：)∈D，1≤k≤K，对切片YFTV(i1，i2，：)∈D进行PCA重建，得到对应的重建切片D。

(10)

式中：y∈D为重建前的测试集原始向量，y对应的广义重建向量的中心切片为表示向量的Frobenius范数；D为向量y中的标量个数(即原始图像像素数量)；MAX为y中所有像素的最大可能值，MAX=255。

基于TPCA的向量重建算法如下：

输入：广义向量XTV，1，XTV，2，XTV，3，…，XTV，K，YTV∈CD≡I1×I2×D，其中广义标量尺寸为I1×I2。

①计算傅里叶变换XFTV，k←F(XTV，k)，1≤k≤K，YFTV←F(YTV)。

② for 1≤i1≤I1do

③ for 1≤i2≤I2do

④计算协方差矩阵G：

⑤计算协方差矩阵G的奇异值分解：G=U·S·VH。其中，复数矩阵U∈D×D，S∈D×D，V∈D×D，VH表示复数矩阵V的共轭转置。

⑦ end for

⑧ end for

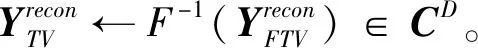
3 实验

本实验涉及的图像来源于公开的手写数字数据库MNIST。MNIST数据库在各种图像处理系统及机器学习领域的训练和测试中被大量使用[9-10]。MNIST数据库中每张图像都是分辨率为28×28的灰度图，本研究的训练集采用类别为0～9的图像各60张，共600张，测试集中包含类别为0～9的图像各10张，共100张。

图2 基于PCA和TPCA拼接矩阵的PSNRFig.2 Splicing matrix PSNR based on PCA and TPCA

表2 基于PCA和TPCA拼接矩阵的部分PSNR数据Tab.2 Splicing matrix PSNR based on PCA and TPCA dB

随后又对比了在特征维数为250和500的条件下，测试集使用PCA和TPCA得到的100幅重建图像的PSNR，见图3和图4。按照PCA的PSNR由小到大的顺序，100幅图像的序号被标记为1～100，广义标量被扩展为2阶数组的TPCA用TPCA(2阶广义标量)表示，TPCA(4阶广义标量)表示广义标量为4阶数组时的TPCA，广义标量为6阶数组时用TPCA(6阶广义标量)表示。图3和图4中广义标量取不同阶数时部分重建图像的PSNR如表3、表4所示。在特征维数为250的情况下，手写数字“3”使用不同方法得到的重建图像如图5所示。由图3至图5及表3、表4可以观察到，当特征维数保持不变时，基于TPCA的重建效果明显好于PCA，且随着广义标量阶数的升高，TPCA的重建结果得到进一步优化。具体地，当特征维数为250时，TPCA(6阶广义标量)的PSNR较PCA(0阶广义标量)提高近20 dB；当特征维数为500时，TPCA(6阶广义标量)的PSNR较PCA(0阶广义标量)提高近30 dB。

图3 特征维数为250时基于PCA和TPCA重建图像的PSNRFig.3 PSNR of reconstructed image based on PCA and TPCA when the feature dimension is 250

图4 特征维数为500时基于PCA和TPCA重建图像的PSNRFig.4 PSNR of reconstructed image based on PCA and TPCA when the feature dimension is 500

表4 特征维数为500时基于PCA和TPCA重建图像的部分PSNR数据Tab.4 PSNR of reconstructed image based on PCA and TPCA when the feature dimension is 500 dB

图5 特征维数为250时手写数字“3”在不同方法下的重建效果Fig.5 The reconstruction results of the handwritten digit "3" with feature dimension of 250 under different methods

4 结语

为验证TPCA较PCA在特征提取和降维重建方面的性能优势，本研究进行了灰度图像的重建实验。结果表明：在相同条件下，TPCA算法与经典PCA算法相比对图像的重建效果更好，并且当广义标量为6阶数组时，图像重建结果又继续得到优化。此外，受图像尺寸的限制，当选取超出原始图像范围的像素邻域时，像素邻域需由0填充；若所选取的邻域像素都已为0，继续增大广义标量的阶数或尺寸就会增加冗余的图像信息。