扩展高斯图像聚类的缺失点云配准

吴庆华，蔡琼捷思，黎志昂，刘嘉程

（1. 湖北省现代制造质量工程重点实验室，湖北武汉430064；2. 湖北工业大学机械工程学院，湖北武汉430064）

1 引 言

点云配准是虚拟现实、三维测量、机器人视觉引导等领域中的一项关键技术［1］。配准主要分为手动和自动两大类。前者是通过贴上标记，计算标记点在不同视角下的位置关系矩阵；后者是通过描述子或者形状关系，进行迭代查询最优位置关系矩阵［2］。目前，自动配准需求广泛，是点云配准的研究热点。然而，受物体表面形貌和纹理特性等因素影响，所获取的三维点云往往存在局部数据丢失、噪声和乱序等问题。这类问题会影响点云的配准精度和时效，对此许多学者开展了大量研究工作。

自动配准算法中运用最广泛的是由Besl 等提出的最近点迭代算法（Iterative Closest Point，ICP）［3］，该算法通过迭代求解出最小误差时的对应点对之间的变换关系。虽然该算法精度很高，但需要良好的初值来保证收敛性。所以，自动配准一般先采用粗配准获得初值，再用ICP 进行精配准，因此，如何将点云变换到ICP 的收敛域成为解决问题的关键［4］。Radu Bogdan Rusu 等［5］提出了快速点特征直方图（Fast Point Feature Histograms，FPFH）的特征量，以点与其邻域点法向量夹角等信息为特征构建直方图，并实现了三维点云的粗配准。该方法对大多数点云具有较高的配准精度，但耗时长，特别是对于存在异常法向量夹角等信息的缺失点云更难以收敛；Salti S［6］提出基于方向直方图的编码统计特征（Signature of Histogram of Orientation，SHOT）点云配准算法，该算法同时具有直方图特征的抗噪性和基于标签特征的鉴别性，且对旋转和尺度具有不变性，其局限性在于仅适用于含有大量不同曲率特征的缺失点云；王欣［7］使用边界生长法提取点云的边界点云，通过匹配边界点云实现粗配准，对于缺失点云，由于其边界并不完整容易使配准失效；Magnusson M 提出的正态分布变换（Normal Distributions Transform，NDT）算法［8］，该算法耗时稳定，并且初值误差大也能很好的纠正，但对缺失点云，由于局部区域统计结果会产生异常，导致配准效果不佳。

缺失点云的局部数据存在丢失，会造成其局部法向特征、边界特征和重叠度等发生一定程度的改变。这些改变会导致大部分算法的收敛速度、配准精度和适用性产生不同程度的影响。扩展高斯图像聚类可以有效地提取出法向特征相似且重叠度较大的子点云，且对局部点云缺失并不敏感［9］。为此，本文提出了基于扩展高斯图像聚类（Clustering Extended Gaussian Image，CEGI）的缺失点云配准算法。该算法对于缺失点云具有较高的配准精度，可以有效的避免上述问题带来的影响。

2 C-EGI 点云配准算法原理

C-EGI 算法的基本思想是将点云通过高斯映射得到扩展高斯图像（Extended Gaussian Image，EGI）；然后，对EGI 聚类分割，并对分割后的聚类进行匹配；将匹配结果逆高斯映射后，进行粗配准；最后，使用粗配准结果更新源点云，再和模板点云进行精配准，如图1 所示。其关键在于分割后的聚类匹配和粗配准关系求取。本文采用体积-模长算子（Volume-norm Operator，VN Operator）对分割后的聚类进行匹配；使用基于距离-曲率描述子（Distance-curvature Descriptor，DC Descriptor）查询对应点对，实现粗配准。

2.1 基于VN 的聚类匹配

基于VN 的聚类匹配分为两个部分，EGI聚类分割和基于VN 匹配分割后的聚类。EGI 是将三维物体的一点通过高斯映射至单位球面上的一点，并在该点上添加一个向量，向量的方向与该点的法向量方向一致，模长为该点所在面的面积［9］。并且，法向相近的点会区域性集结，如图2所示，（a）表示长方体与其扩展高斯图像的对应关系，（b）表示空间曲面与其扩展高斯图像的对应关系。

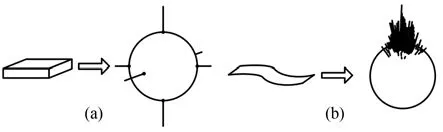
图2 三维物体映射扩展高斯图像示意图Fig. 2 Diagram of 3D object mapping to EGI

在获得EGI 之前，需要估算点云中每个点的法向量。取点Pi(xi，yi，zi)与邻域点云集N{Pi}，采用最小二乘法拟合出Pi点的平面方程z=Ax+By+C［10］，利用公式（1）求出该平面方程的偏差平方和d：

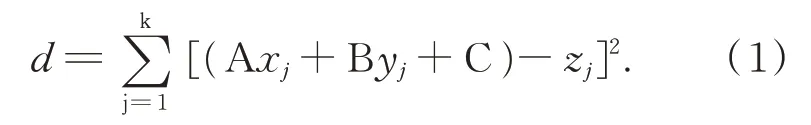
取d最小值时所对应的向量n(A，B，C)作为点Pi(xi，yi，zi)的法向量。然后，进行高斯映射，获得对应EGI，并对EGI 使用欧式聚类。

为确保聚类后源点云和模板点云的高斯点云簇是相对应的，本文采用基于VN 算子进行匹配。其定义函数为：

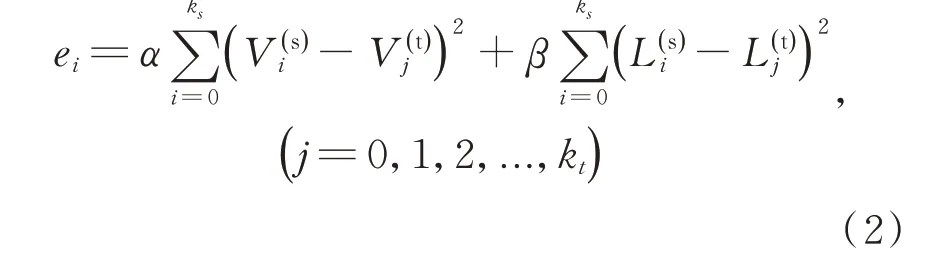
其中：Vi表示每个簇的体积，Li表示每个簇的向量总模长，α和β为自定义权重系数。

2.2 基于DC 的粗配准

由于EGI 只能反映三维物体的旋转姿态关系，无法反映出三维物体的空间位置关系［11］。本文对最优高斯点云簇对使用索引查找的方式进行逆高斯映射，获取对应的实体点云对，进行对应点对求解。由于此时点云的法向特征相似，重叠度较高，并且数据集大幅下降，使用传统算法进行对应点对的求解优势并不明显，所以本文提出一种基于DC 描述子的粗配准方法。

首先，通过DC 描述子进行对应点对的查询，其定义函数为：

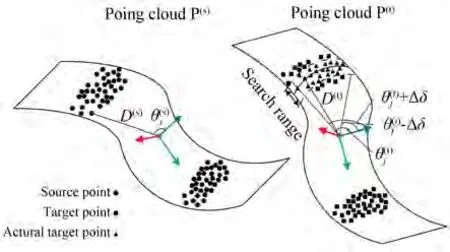
图3 对应点对查询示意图Fig. 3 Diagram of querying corresponding point

3 C-EGI 配准算法设计

本文算法总体流程如图4 所示。主要分为两部分：

3.1 粗配准矩阵求解

首先，对实际扫描点云S和模板点云T使用高斯映射获得EGI，对EGI 进行聚类，通过基于VN 的匹配获得最优簇对；其次，在逆高斯映射后，通过DC 描述子求解对应点对，并使用RANSAC 算法剔除异常点对；最后，采用SVD 算法计算出粗配准矩阵RcTc。

3.2 最终配准矩阵求解RcTc

将源点云S 进行矩阵变换乘以后获得点云S′，对S′ 采用ICP 算法计算出精配准矩阵RfTf。利用公式（5）求解最终配准矩阵RT。

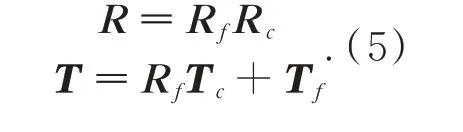
4 实验结果与分析

实验运行环境为IntelCore 2.4GHz CPU，PCL 1.8.0 平台，实验数据来自于斯坦福大学激光扫描数据库中的bunny（35947）模型和实际采集点云。分别进行了一般点云配准实验、缺失点云配准实验和散放棒料抓取中的点云配准实验。

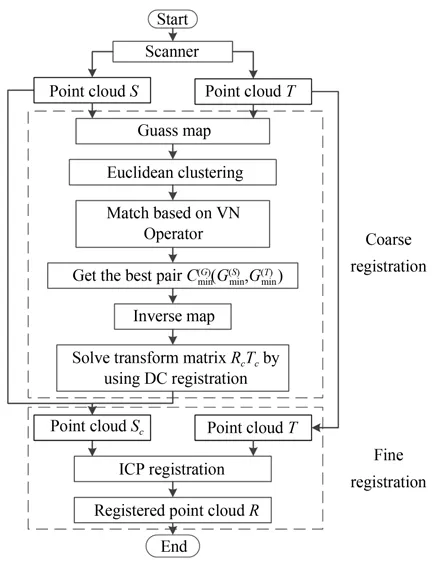
图4 算法流程图Fig 4 The algorithm flowchart

实验分别使用FPFH，NDT，SHOT 和本文算法，结合ICP 精配准算法进行配准实验比对，为了使实验更有说服力，设置各实验模型原始点云（模板点云）密度的10 倍作为各算法搜索半径；NDT 网格内点云数量设为10，步长设置为0.1；为减小ICP 算法受到数据局部缺失的影响，采用缩小ICP 算法的最近点搜索范围的方法，设置ICP 算法的搜索半径为模型原始点云密度的5倍。采用配准后对应点之间的距离d的均方误差（Mean Square Error，MSE）作为配准评价标准，如式（6）所示：

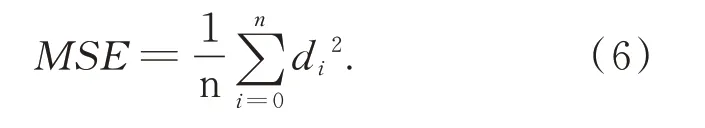
4.1 一般点云配准实验

对Bunny（35 947）点云进行旋转变换，获取不同姿态的点云，任取3 个姿态分别使用C-EGI，FPFH，NDT，SHOT 进行配准测试。

图5 为各算法配准效果，表1 和表2 为各算法的配准精度与耗时。从表1 和表2 中可知，FPFH算法拥有较高的配准精度，但是耗时长。SHOT算法相比FPFH 精度稍有下降，但速度优势明显。NDT 算法相对SHOT 算法精度相近，但耗时相对较高。本文算法精度与SHOT 算法相近，但速度提升近31.1%。

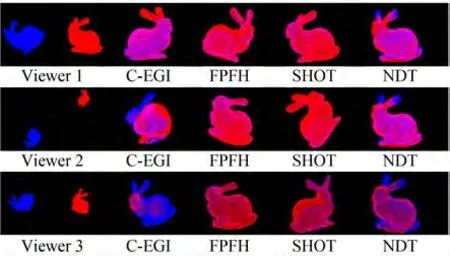
图5 各算法配准结果Fig. 5 Registration result of different algorithms

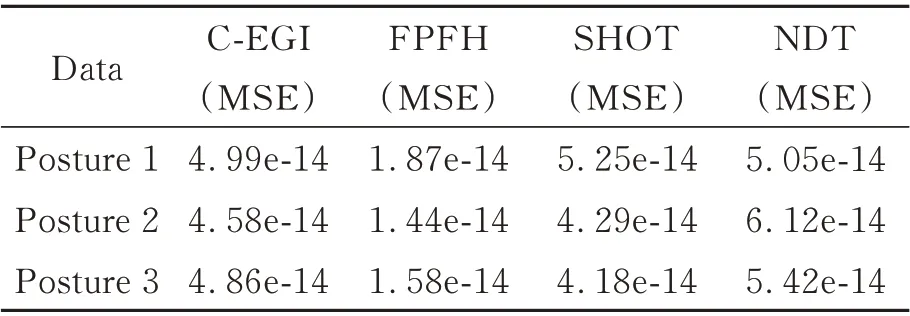
表1 配准精度实验误差对比表Tab. 1 MSE of registration experiment （mm2）

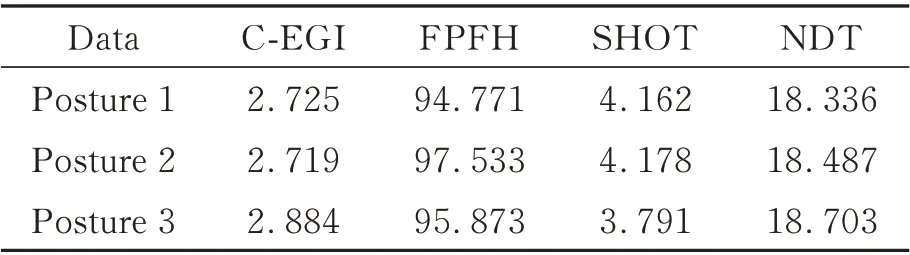
表2 配准精度实验耗时对比表Tab. 2 Running time of registration experiment （s）

4.2 缺失点云配准实验

本实验分两步验证，首先验证本文算法的精度和时效性，然后验证本文算法的稳定性。4.2.1 缺失点云配准精度和时效性实验

由于物体表面材质、纹理和光线遮挡，获取的点云数据常常存在数据丢失。故设计缺失点云实验，对各算法进行配准测试。分别采用统计阈值T=0.1 和T=0.5 的统计离群点滤波过滤相对稀疏部分，模拟物体自身形貌遮挡或表面反光导致的数据丢失；分别使用X轴方向和Z轴方向直通滤波过滤40%左右的截面数据，模拟光线受到遮挡导致的数据丢失。

图6 为各算法对缺失点云的实际配准效果，表3 和表4 为各算法对缺失点云的配准精度与耗时。从表3 和表4 中可知，NDT 算法对缺失点云已不能有效的配准。FPFH 算法对于缺失点云配准精度依旧稳定，但是耗时更长。对于SHOT 算法而言，精度相对FPFH 算法较差，但耗时缩小了近70 倍。本文算法与FPFH 算法精度相当，并且相对SHOT 算法速度提升了近

38.7%。

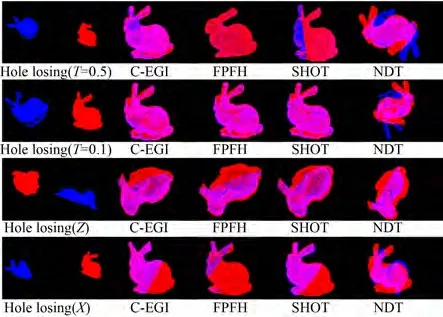
图6 缺失点云配准实验各算法结果Fig. 6 Registration result of different algorithms with losing point cloud

表3 缺失点云配准实验误差对比表Tab. 3 MSE of registration experiment with losing point cloud（mm2）

4.2.2 缺失点云配准稳定性实验

本文算法是利用基于扩展高斯图像聚类提取相同特征的子点云进行配准，如图7 所示，（a）为模拟孔洞缺失时的扩展高斯图像聚类提取的子点云示意图，（b）为模拟截面缺失时的扩展高斯图像聚类提取的子点云示意图。

为验证其可以稳定有效地规避点云局部缺失带来的影响。本实验采用与精度实验相同方法，通过统计滤波和直通滤波模拟孔洞缺失和截面缺失。

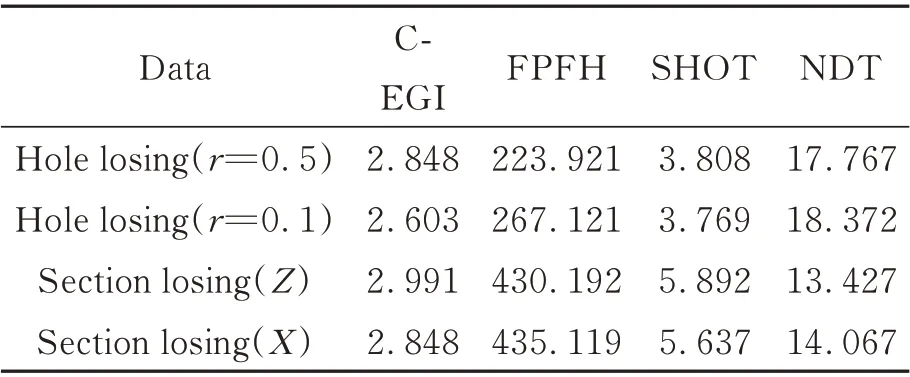
表4 缺失点云配准实验耗时对比表Tab. 4 Running time of registration experiment with losing point cloud（s）

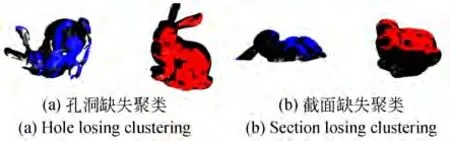
图7 扩展高斯图像聚类结果Fig. 7 Clustering result of Extended Gaussian Image

分别对源点云进行9 组不同阈值的统计滤波和X 轴直通滤波后与同一模板点云进行配准实验，实验结果如图8 和9 所示，采用缺失点数的占比区分各组数据。从图8 和9 可知，本文算法在9组不同孔洞缺失和截面缺失下的进行配准实验，实验结果都显示本文算法能获得良好的配准效果。因此，该算法针对局部孔洞缺失和局部截面缺失两种情况均具有良好的鲁棒性。

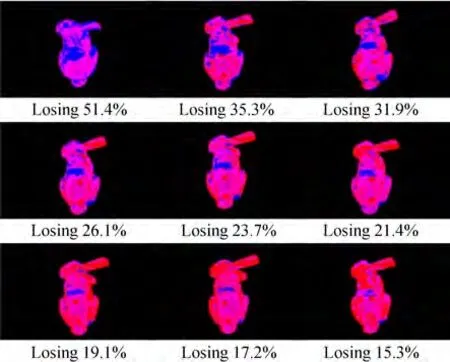
图8 孔洞缺失点云配准稳定性实验结果Fig. 8 Robust result of registration experiment with hole losing point clouds

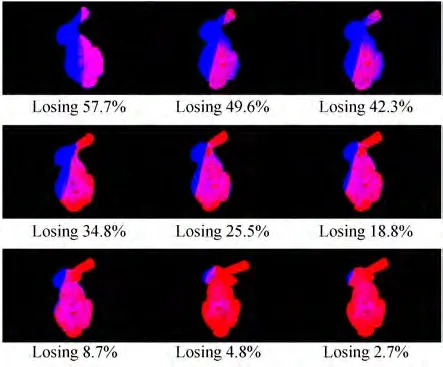
图9 截面缺失配准稳定性实验结果Fig. 9 Robust result of registration experiment with section losing

4.3 散放棒料抓取中的点云配准实验

本实验采用3D 扫描仪和散放棒料零件进行测试，如图10 所示，从实际扫描点云中任取五个姿态不同棒料作为实验对象进行配准测试。

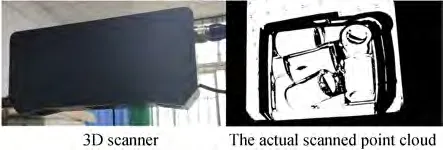
图10 实验仪器及扫描结果图Fig. 10 Experiment instrument and the scanned result

图11 为各算法对散放棒料抓取中的点云的配准效果，表5 和表6 为各算法对散放棒料抓取中的点云的配准精度和耗时。从表5 和表6 中可知，NDT 算法配准精度较差且耗时较长。FPFH算法由于该点云特征单一且存在缺失，使得在时效性和精度两个方面结果都不佳。SHOT 算法相比NDT 和FPFH 精度较优，并在耗时上具有明显优势。本文算法在精度方面优于这三种算法，在评价误差上优于FPFH 算法17.9%，并且在平均耗时方面相比SHOT 算法提速近26.4%，可见本算法能满足实际缺失点云配准要求。

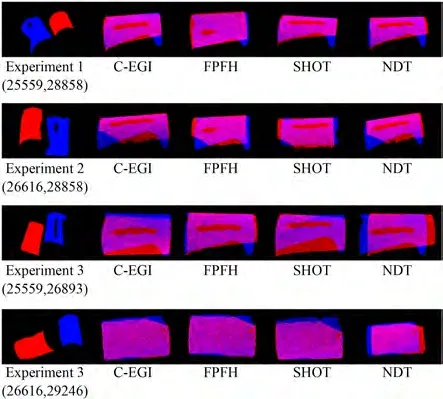
图11 实际点云配准实验各算法结果Fig. 11 Registration result of different algorithms with actual point cloud

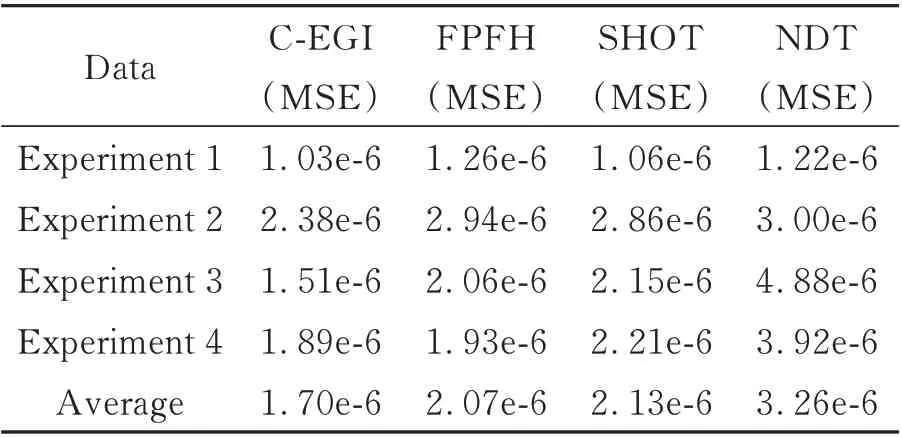
表5 实际点云配准实验误差对比表Tab. 5 MSE of registration experiment with actual point cloud（mm2）

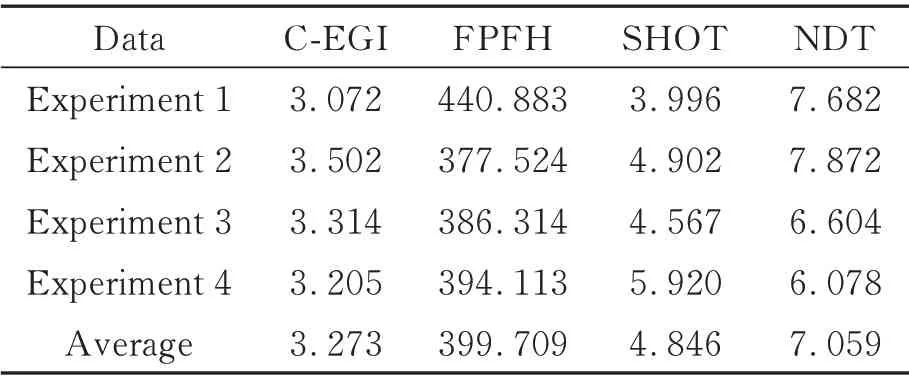
表6 实际点云配准实验耗时对比表Tab. 6 Running time of registration experiment with actual point cloud（s）

5 结 论

本文针对缺失点云提出了一种基于扩展高斯图像聚类的配准算法，实现了对缺失点云的快速高效配准，可以满足一般物体扫描时存在数据丢失的点云配准要求。通过把点云映射到EGI中聚类再逆映射回实体点云的方法进行配准，根据实验结果证明该方法可以有效的避免点云由于扫描仪视角、物体材质和扫描环境等因素带来的影响。并且，与传统配准算法相比，具有更好的精度和时效性。

但由于本算法运用了较多的参数进行计算，并且利用EGI 进行聚类，所以本算法的参数选取和法向方向判断是一个重要因素，对于如何自动调节最优参数和法向统一是本算法未来研究的重要方向。