大离轴量非球面反射镜的加工方法

陈宝华，吴泉英*，唐运海，范君柳，王 军，孙 毅

（1. 苏州科技大学物理科学与技术学院，江苏苏州215009；2. 苏州苏大明世光学股份有限公司，江苏苏州215028）

1 引 言

离轴非球面反射镜是先进光学系统朝着小型化和高性能方向发展必不可少的组成部分之一。其应用有效避免光学系统中心遮拦并改善相应的衍射问题提高成像质量，特别是大离轴量反射镜能够增加工作焦距和光路折转角度，在空间光学成像和激光切割应用等领域中起着关键性作用［1-2］。

目前，国内外对于口径不大且偏离光轴中心的中小型离轴量非球面反射镜，通常借助由直线进给轴—X轴和Z轴，加上一个旋转主轴C轴组成的单点金刚石车床（SPDT）常规回转车削实现［3］，例如国外索雷博光学元件公司，国内的长春光学精密机械与物理研究所、天津大学和苏州大学等。为了达到更高的面型精度，一种子母同体的离轴非球面反射镜加工方式被提出［3］，将待加工的小子镜嵌入大的母镜中一同车削。对于大离轴量反射镜，受限于车床加工口径限制，一般需要通过定制夹具将反射镜中心与旋转主轴中心重合，配合三轴SPDT 下的慢刀伺服技术完成。而加工那种两端矢高差与其直径比值接近1，光路折转角度为90°的大离轴量反射镜，易造成Z轴在一个周期内的振动幅度较大，产生大的跟踪误差，且刀具后角易与光学面触碰，破坏面型，降低反射镜的加工精度。为此，有人提出通过角度变换的方式旋转待加工反射镜［4］，使得边缘矢高差与其直径的比值降至最低，随之利用夹具与旋转主轴中心重合后车削加工，这样虽能解决上述问题，但难以避免角度定位误差，增加了后期的装调难度。

为了改进大离轴量非球面反射镜的加工方式，本文提出一种高效率、低误差，适用于任意离轴量且不受车床加工口径限制的反射镜车削及刀具路径规划方法。此方法以坐标平移变换代替角度旋转，减小后期的装调误差；平移变换后的反射镜以主轴中心为原点，多个与之相同的反射镜均匀分布在圆周上，一次加工即可车削多个，效率高；同时提出一种基于样条与正弦混合插值的刀具路径规划方法，解决断续光学面刀具路径不平滑、切削速度不连续问题，相对于现有技术，加工质量和效率均得到提高。

2 模型建立

如图1，在笛卡尔x-y-z坐标系中，二次离轴非球面反射镜a1的方程可由式（1）定义；

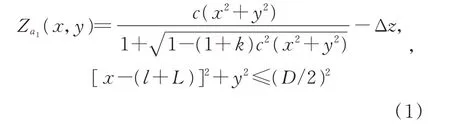
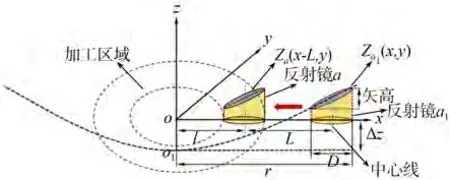
图1 离轴非球面反射镜模型Fig.1 Off-axis aspheric machining model

其中：c=1/R，R是非球面镜的顶点曲率半径，k是圆锥系数，Δz是非球面沿光轴Z的移动距离，由离轴反射镜a1的设计厚度决定，D是反射镜a1的直径，l+L是离轴量，O是坐标原点，O1是非球面顶点，r是a1边缘与原点O之间的距离。

设车床极限加工口径为d，当2r＞d时，以旋转对称车削方式无法完成反射镜a1的加工，此时将a1沿着x轴平移L距离得到离轴反射镜a，此方程可表述为［5］：

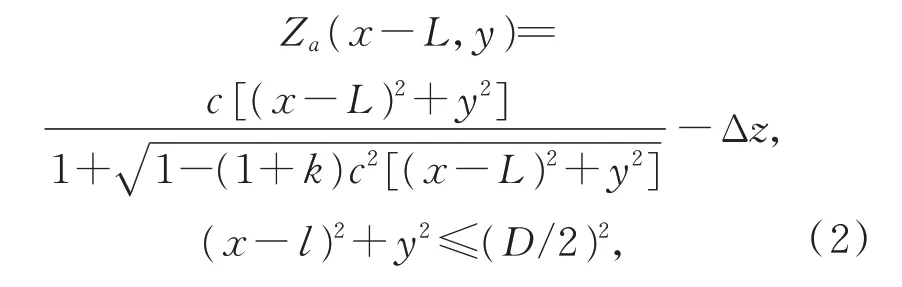
其中：l是反射镜a中心与原点O之间的距离，且l＜d/2。

为了合理地规划刀具路径，并兼顾效率及主轴的动平衡，以原点O为中心，l为旋转半径，将反射镜a在加工区域对称分布，如图2 所示的是离轴反射镜在x-y平面上的投影，设反射镜阵列个数为N，l需满足式（3），以确保子镜之间不重叠：

从图2 可以看出，在相邻的切削区之间存在一定的过渡区域，切削区的面型特征可由公式（2）转换得到。

过渡区刀具路径需要采用人工方式补偿，切削区与未补偿的过渡区矢高不一致，在慢刀伺服工作模式下，运行曲率有突变的边缘交界处Z 轴存在剧烈跳变，造成C轴瞬间停顿，此处面形粗糙度较大，影响精度。为了保证整个加工区域刀具轨迹圆滑连续，Z轴和C轴相对切削速度连续和加速度无突变，首先在慢刀伺服工作模式下根据已知切削区面型矢高特征Za，结合样条和正弦混合插值建立第n圈刀具路径刀具轨迹方程［6］，设：

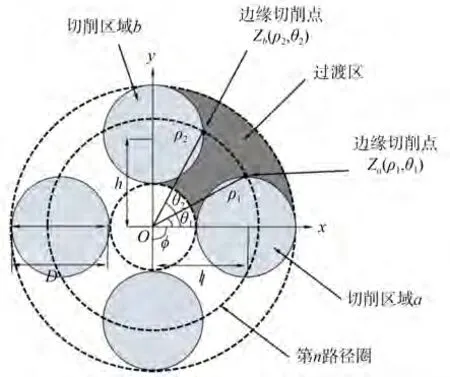
图2 离轴反射镜投影Fig.2 Off-axis aspheric mirror projection

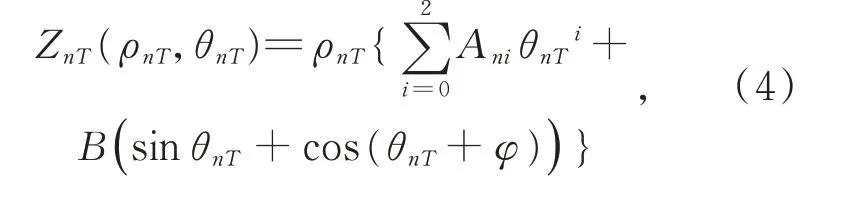
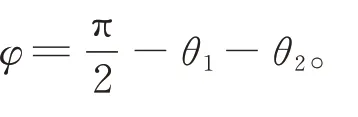
若同一路径圈内ρ1和ρ2相等，则ρnT=ρ1；而按照阿基米德螺线渐变时，

ρnT由如式（5）所示定义：

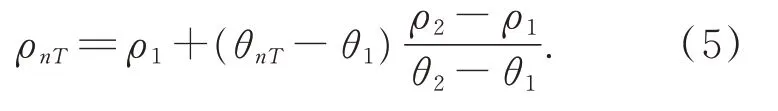
在一个切削-过渡-切削区域内，待求系数Ani和B的求解需满足如下边界条件：

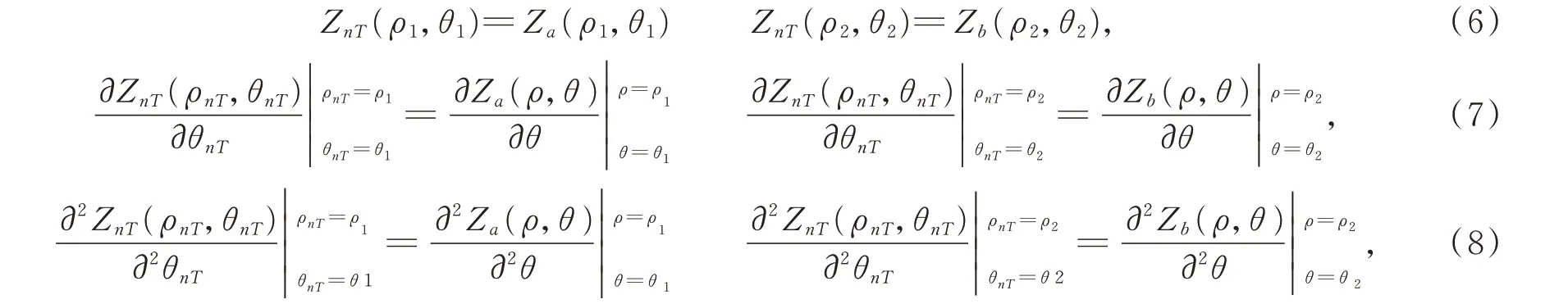
其中(ρ1，θ1)和(ρ2，θ2)是切削区-过渡区边缘切削点（刀具轨迹）在x-y面上的投影极坐标。

通过公式（6）约束切削区-过渡区边缘切削点，使两者矢高相等，保证整个加工区域平滑。在实际加工过程中，车床Z轴与C轴联动方式具有以下特点，设车床C轴旋转角速度为ω，车床Z轴的进给速度νz可表示为：

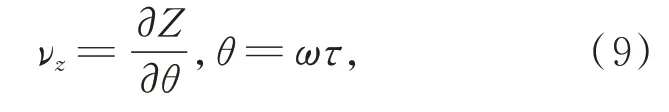
其中：τ为时间，由于在公式（7）中约束过渡区和切削区边缘处导数相等，因此当角速度ω恒定时，车床Z 轴的进给速度νz在过渡区和切削区都是一条连续的曲线，这样可以使切削相对速度连贯。

同样地，设车床Z轴的进给加速度αz为：

公式（8）中约束过渡区和切削区边缘处二阶导数（即进给加速度αz）相等，因此其加速度αz在整个路径圈内也是一条连续的曲线，保证慢刀伺服工作模式下主轴C的转速平稳，提高效率和切削精度。

SPDT 加工刀具为单晶圆弧车刀，因此在加工之前需要对每个路径圈上的各个切削点作刀具曲率半径补偿。图3 是补偿方式示意图，刀具安置在车床Z轴，刀尖圆弧位于x-z平面。对于切削区，其上的任意切削点P（x，y，z），对应的刀具中心刀位点P1（x1，y1，z1）可由如式（11）计算得出：

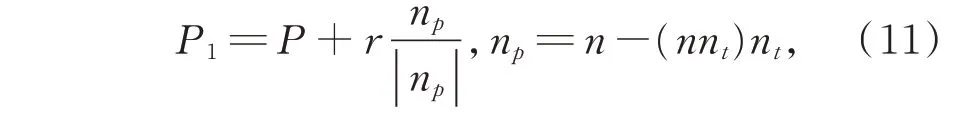
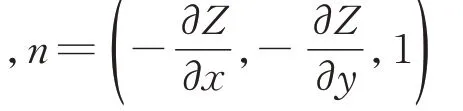
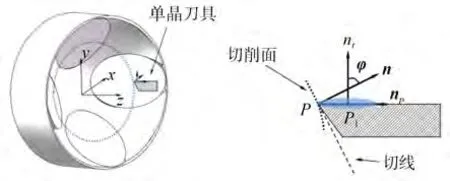
图3 刀具半径补偿Fig.3 Tool radius compensation

3 实验及分析

为了分析整个加工区域的刀具路径、切削时的Z 向速度和加速度，设定离轴非球面反射镜的各项参数如表1 所示。反射镜阵列个数为4，截取极径ρn=50 mm 路径圈上的Z向路径，在未对过渡区处理的情况下，切削区的路径分布如图4所示。图4（b）中的横坐标为C轴转动的角度（°）。纵坐标为矢高Z（mm）。切削区面上的路径分布类似半个周期的正弦曲线，由于过渡区未作补偿处理，在C轴转动角度30°～70°之间时路径缺失，无法完成加工。在补偿时可以选择多种插值方式，例如直线插补，抛物线插补等。以直线插补为例，采用直线插补的过渡区矢高基本保持不变，而切削区矢高类似正弦波动，这种插值方式的过渡-切削端面处存在明显的突变，导致交界处Z轴剧烈跳动，造成此处面形粗糙度较大，不利于切削稳定和精度保证。结合上述公式（4）～公式（8），采用样条和正弦混合插值的形式，补全过渡区，如图5。补全后的过渡区和切削区完整结合在一起，交界处平滑连续，在一个过渡-切削周期内，Z轴的振动幅度大约9 mm，此时的极径ρn接近反射镜中心位置，因此整个加工过程中Z轴的振动幅度不超过10 mm，极大减少车床运行过程中的跟踪误差，图5（b）是三维图。

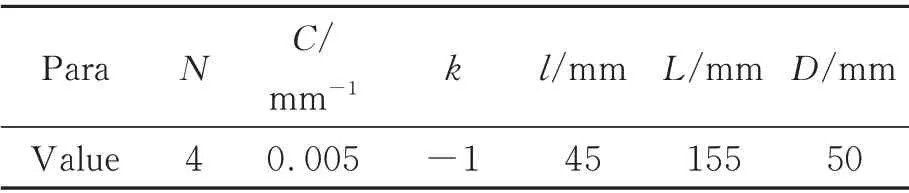
表1 离轴非球面反射镜各项参数Tab.1 Parameters of off-axis aspheric surface

如图6（a），横坐标同样是C轴转动的角度，纵坐标是Z向切削速度。在离轴反射镜中心位置，即当C轴转动接近0°，90°等角度时，其矢高Z变化最缓，切削速度接近0；而在30°和70°左右位置的反射镜边缘处，矢高变化较为剧烈，切削速度最大。在一个路径周期内，根据公式（7）条件约束，外加本文提出的过渡区路径为连续的初等函数，因此车床Z轴的Z向切削速度Vz在整个加工区域连续无突变。车床Z轴切削加速度与C轴转动角度的关系曲线如图6（b）所示，图中横坐标单位为度，纵坐标单位为加速度a。其中30°～70°附近的转角区间曲线是过渡区的Z向切削加速度，70°～110°附近的转角区间曲线是切削区的Z向切削加速度，其最大值约为0.02 mm/（°）。在一个周期的切削-过渡路径期间，车床Z轴切削加速度呈现为一个两端点连续且对称分布的平滑曲线，有利于车床平稳运行。图7 是整个加工区域未作刀具曲率补偿前的刀具路径和反射镜模型的三维图，图8 是补偿后刀具路径。

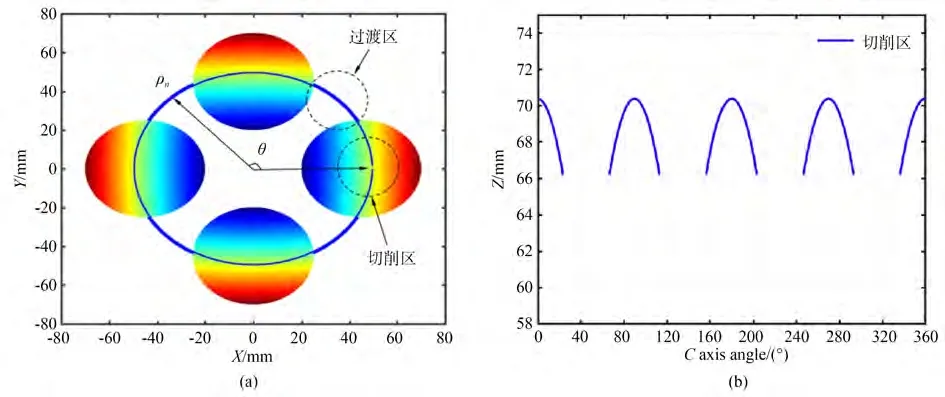
图4 第ρn圈刀具路径Fig.4 Tool path under current polar ρn

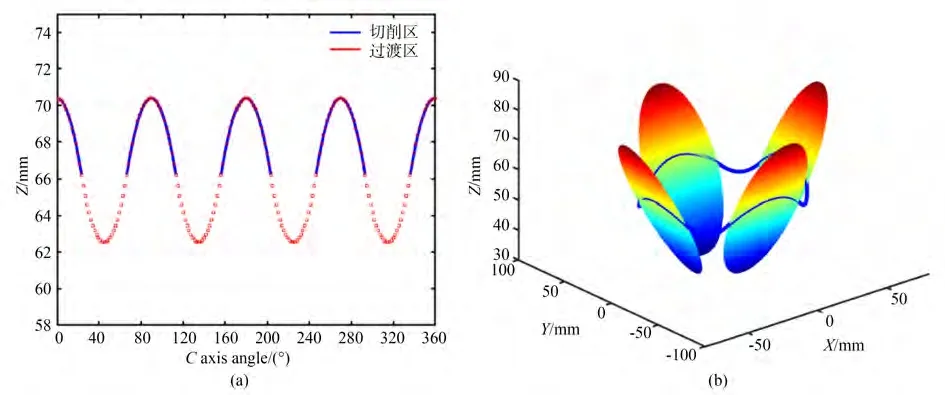
图5 补全后的第ρn圈刀具路径Fig.5 Complemented tool path under current polar ρn

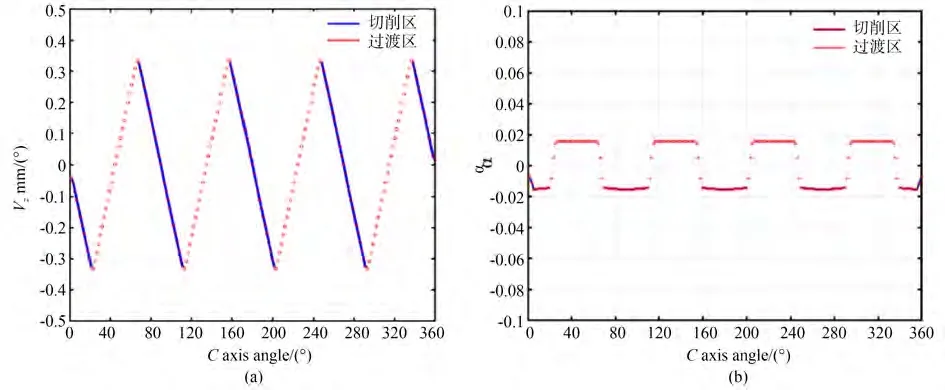
图6 Z 向切削速度和加速度Fig.6 Z-direction cutting speed and acceleration

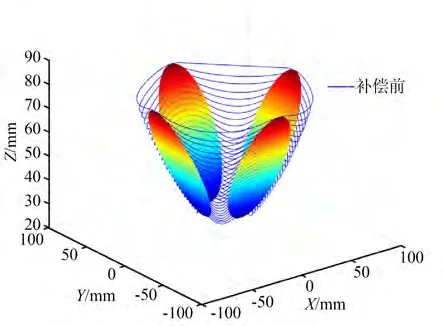
图7 刀具曲率半径补偿前的刀具路径Fig.7 Complete tool path before compensation

图8 刀具曲率半径补偿后的刀具路径Fig.8 Complete tool path after compensation

为了研究该方法在实际慢刀伺服车削中的可行性及精度情况，以离轴反射铜镜为例［7］，设定表1 中的阵列个数N=3，其余参数不变。加工车床为美国Moore250UPL，极限加工口径300 mm。加工时的切削参数如表2，刀具曲率半径r=0.8 mm，相邻路径间隔Δl=10 μm，采用等角度离散加工，角度采样间隔Δθ=0.5°，切削深度Δs=2.5 μm，车床加工速度RPM=46 r/min 左右，整个加工过程中刀具运动的最大矢高Sagmax=7.8 mm。

图10 是采用ZYGO 干涉仪配合无像差点法检测加工完成的离轴反射面面型［8-9］，测量时去除Pistion，Tilt 和Power 得到的PV 值是0.41 波长@632.8 nm，这是刀具路径多次修正补偿后的结果［10］，其中去Power 的实质是拟合反射镜的曲率半径，达到轻微的离焦效果，而光学设计中的公差分析允许曲率有一定程度上的上下浮动，去Power 的曲率拟合误差小于此浮动值。

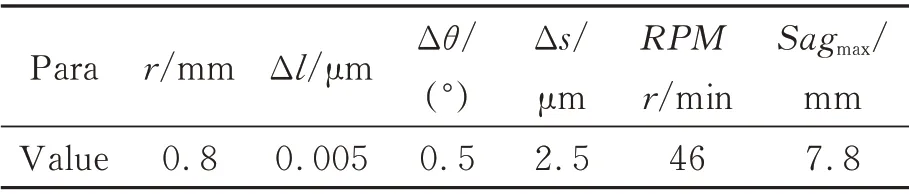
表2 切削参数Tab.2 Cutting parameters

图9 实物加工Fig.9 Machining structure

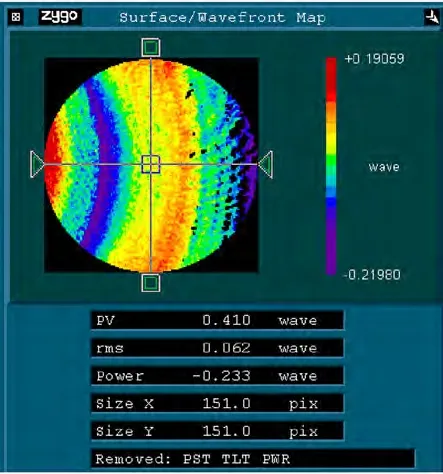
图10 干涉图Fig.10 Interferometer detection

在实际刀具路径规划中，可以先对切削区完成刀具曲率半径补偿，再结合方程（4），补全过渡区，这样一来可以消除刀具曲率半径补偿带来的Z向切削速度不连续。由于过渡区不存在，刀具在切削-过渡区运动时受力不均会产生轻微的震刀现象，外加慢刀伺服本身C轴转速慢，切削线速度远小于常规回转车削，因此波面图存在明显的刀纹，难以避免粗糙度在一定程度上的降低。震刀现象几乎存在于所有的非圆对称光学面加工，一般与反射镜材料、边缘厚薄、切削速度和刀具锋利程度等相关，本文中的震刀现象应该是刀具使用时间过长，不够锋利导致。为了减少实验时间，本文选取的路径间隔是10 μm，其粗糙度是间隔5 μm 的4 倍，适用于红外成像或照明光学系统。若想提高表面粗糙度，可以通过减小路径间隔，后期作表面抛光则为更好的选择。

4 结 论

本文以实际大离轴量非球面反射镜样品的加工为例，选取合适的反射镜平移距离减小刀具离轴，无需角度变换，降低装调误差，优化加工工艺；分析建立的样条和正弦混合形成的过渡区刀具路径，从理论和实验上证明过渡区路径和切削区路径能够平滑衔接，在整个加工区域，刀具的Z向切削速度和加速度连续无突变，满足Z轴和C轴平稳运行。最后通过光学无像差点法的干涉检测，加工精度达PV0.41 波长@632.8 nm 且一次加工可完成多个反射镜，效率高。此外，此方法还可以补全其它断裂面车削问题，例如一体镜（要求主反射镜和次反射镜位于同一母镜，一次加工成型）。当然也存在一定的不足之处，例如反射镜平移的距离不宜过大，即加工区域过小，容易造成刀具后角干涉，触碰光学面；但平移距离小，加工区域又会变大，同样会造成较大的加工误差，因此合适地选择平移距离对加工精度的提高有重要作用。另外，在刀具曲率半径补偿时，由于整个加工区域是阵列的，其面型在一个周期内变换多次，造成曲率半径补偿后的X轴周期性进给，而X轴是承重轴，这会带来不小的跟踪误差，虽可以通过补偿Z轴，达到X轴线性移动的目的，但也会导致程序繁琐，难以保证实际精度，对最终的加工精度有一定的影响。