一种融合用户偏好和社交活跃度的推荐算法 *
2021-07-02李玲玲
李玲玲 ,黄 俊,王 粤
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
随着物联网、云计算的不断发展,人们面临的信息量呈爆炸式增长,如何在短时间内为用户提供有效的个性化推荐尤其重要。协同过滤便于理解,适用于各种行业,是当前推荐系统中运用最常见的方法之一,其主导思想是将用户过去的行为信息进行挖掘与分析,以获得用户偏好[1]。协同过滤算法通常可以分为基于内存和基于模型两类方法。基于内存的协同过滤已经在各种商业平台得到了最大化使用[2],主要是从用户或者项目的角度进行推荐。基于模型的方法主要是通过使用机器学习算法[3],对数据的训练集进行训练以建立模型,并使用训练好的模型给用户推荐可能喜欢的项目[4]。由于该方法对数据信息进行了训练,与基于内存的方法相比具有更好的性能。其中,基于矩阵分解的模型受到了研究者们的广泛关注。比如,Mnih[5]将用户评分信息与概率矩阵相结合来进行推荐;Ma[6]、Jamali[7]、Yang[8]通过分析用户评分和社交网络中的用户关系,并与矩阵分解模型中用户特征向量融合,完成推荐。
虽然将协同过滤算法运用在推荐系统中已经获得了较好的效果,推荐质量也提高了很多,但在实际生活中仍然存在着一些难以解决的问题:一是数据稀疏性问题;二是恶意推荐问题;三是推荐精度不高。针对这些问题,大量学者对社交关系以及社交网络中朋友的选择进行了深入研究[9-10],发现其对推荐质量有很大的帮助。
在解决数据稀疏和准确度不高的问题时,Li[11]通过直接和间接信任关系构建了社交网络同心层模型,并融入矩阵分解推荐算法中,提高了用户特征矩阵的准确度,从而提高了评分预测的准确性。还有的学者通过引入用户偏好、社交关系和社交活跃度等方法来解决这个问题。比如,王运等人[12]使用了用户评分信息计算隐式的用户偏好,从而得到用户相似度,然后将用户相似度和物品相似度融入到矩阵分解中,并证明了该方法的有效性;Ju等人[13]同时引入了社交关系和信任关系,将社交关系和用户偏好相结合计算得到信任度,然后根据信任度进行评分预测;Ran等人[14]通过社交活跃度描述不同用户对于朋友的影响,并将社交活跃度与矩阵分解相结合,使得通过社交活跃度增强用户间的信任度,从而增加亲密朋友间的关系。
尽管在上述文献中分别使用了用户偏好和社交活跃度,但在计算用户偏好时,没有考虑只有少数评分的用户;在计算社交网络中的信任时,只单纯地将社交活跃度与概率矩阵分解融合,没有考虑用户之间存在的其他新人用户。为此,本文提出了一种融合用户偏好和社交活跃度的概率矩阵分解推荐算法(Probabilistic Matrix Factorization Recommendation Algorithm Combining User Preference and Social Activity,UPSA-PMF)。该算法在使用用户偏好计算用户信任度时,使用了用户间共同已评项目数量在两个用户的总共评分数量的比重来解决评分较少的用户带来的准确度不高的问题。在计算社交网络中的信任度时,考虑了社交网络中活跃的用户在用户信任度中的影响。在得到这两部分信任度后,采用动态组合的方式,精准地提取用户间的信任程度,并与概率矩阵中的用户特征矩阵结合,以便更精准地预测用户特征矩阵,使得预测的评分准确性更高。
1 概率矩阵分解模型

(1)
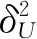
(2)
(3)
式中:I为协方差矩阵。由贝叶斯推导公式可得到用户特征向量Pi和项目特征向量Qj的后验概率为
(4)
将公式(4)最大化得到损失函数最小值,即为最终目标函数,其公式如下:
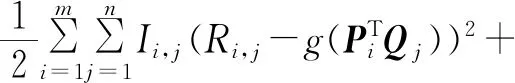

(5)

2 UPSA-PMF算法
根据前面的分析可知,将信任度融入到矩阵分解中,能够较大地改善冷启动和数据稀疏带来的影响,而对不同信任度的充分利用不仅能够提高推荐的可信程度,还能提高评分预测的准确性。分析概率矩阵分解的原理可知,在分解时会分成维度较低的用户和项目特征矩阵,而后对评分值进行预测。因此分解的这两个矩阵越精准,则预测的项目分值越接近用户偏好。在本文中,考虑了提升用户特征矩阵的精准度从而提升预测项目分值的准确度,图1为本文的UPSA-PMF算法图解。

图1 UPSA-PMF算法图解
2.1 基于用户偏好的用户间信任度
在推荐算法中,用户对项目具有评分的行为,根据相关相似度计算方法,可以分析得到用户对不同项目的可能评分情况。
对于用户i和用户t的相似度,若采用Pearson相关系数计算,其计算公式如(6)所示:
(6)

假设用户之间的共同已评项目数量很少,且分值很接近,根据公式(6)便会得到较高的相似度,但结果不准确,因为基数较小,具有偶然性。因此,考虑将用户间共同已评项目数量在两个用户的总共评分数量的比重作为平衡因子Ni,t,改善用户评分数据稀疏的问题,其计算公式如(7)所示:
(7)
传统的Pearson相关系数没有考虑热门项目对相似度带来的影响,使得对所有项目都无差别对待。然而在生活中,热门项目往往反映的都是大众的普遍爱好,不能完全代表用户的个人偏好。相反,如果两个用户对某个冷门项目进行了评分,则更能确切地反映出用户间的偏好相似性。因此,本文在计算用户相似度时,引入热门项目惩罚因子Wi,t,计算公式如下:
(8)
综上,结合了平衡因子和热门惩罚因子的改进Pearson相关系数如公式(9)所示:
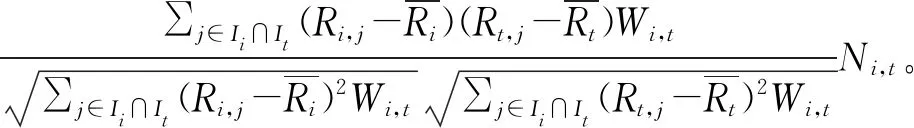
(9)
根据用户相似度,找到偏好相似用户,预测目标用户i已评项目的分数,其计算公式如(10)所示:
(10)

(11)
通过计算用户间在所有共同评过分的项目上的信任度的均值,即为本节所求的基于用户偏好的用户信任度:
(12)
2.2 基于基于社交活跃度的用户间信任度
2.2.1 社交活跃度
社交活跃度是通过用户对朋友意见的依赖程度来表示,可以分析社交网络中不同用户间兴趣偏好的影响。其核心思想有两个:一是如果用户有大量朋友,则表明该用户的社交活跃度较高;二是如果用户的朋友很少是其他用户的朋友,则表明该用户处于活跃状态。
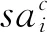
(13)
式中:β为0.15,是PageRank算法的另一种改进算法Personalized PaneRank算法中的取值,主要用来平衡某些用户随机的采纳朋友的意见;η为阻尼系数,通常取值为0.85;Ui是用户i的所有朋友用户集合。从公式(13)可以看出,如果用户有很多朋友,则该用户获得社交活跃度的来源就很多;如果用户的朋友很少是其他用户的朋友,则分母就小,该用户的社交活跃度的比重就越大。
计算社交活跃度时,采用迭代的方式,并把每个用户的社交活跃度的初值设置成1,最大迭代次数cMAX设成60,具体步骤的伪代码如下:
Input:user social relationsS,the maximum number of iterationscMAX,damping coefficientη,initial social activity
Output:social activity of each usersa
1.{ forc=1 tocMAXdo
2. { fori=1 tomdo
5. continue
6.}
7. }
8.}
2.2.2 社交网络中的用户间信任度
在社交网站中,很少通过直接打等级来表示用户间的信任程度,大多数都使用二值型,即信任和不信任。但该方法存在的问题是对用来计算信任的信息太统一,使得不能很好地区分用户对信任用户集合中的用户有什么不同。因此,本文采用SimRank算法[16]计算社交网络中用户间的信任度。令用户i和用户t的信任度为soti,t,指向用户i的所有用户集合为U(i),计算方法分两种情况:
(1)当U(i)=φ或U(i)=φ时,soti,t=0;
(2)在其他情况时,
(14)
式中:η为2.2.1节所用的阻尼系数。
2.2.3 基于社交活跃度的用户间的信任度
在实际生活中,如果用户与非活跃用户建立了朋友关系,则该关系可能会更可靠,Gu等人[17]验证了这个猜想。因此,将社会活跃度作为一个惩罚因子,修正社交网络中的信任度,能到更准确的用户间的信任度。其计算公式如下:
(15)
2.3 融合用户偏好和社交活跃度的用户间信任度的计算
将基于用户偏好的用户间信任度和基于社交活跃度的用户间信任相结合,即得到融合用户偏好和社交活跃度的用户间的综合信任度,其结合方式采用文献[18]的动态调节方法。该方法可以提高对邻居的识别能力,能有效降低数据稀疏,使得推荐质量提高。其计算公式如下:
(16)
式中:nmin和nmax表示两个用户共同评分项目个数的最小值和最大值,n表示两用户间的共同评分项目数。由于该计算公式采用的分段函数,能根据共同评分项目数动态调整基于用户偏好的信任度和基于社交活跃度的信任度的权重,使得最终计算出的信任度会更加准确。
2.4 UPSA-PMF算法
假设用户i根据2.1节、2.2节和2.3节计算出的信任用户集合为Mi,由于用户的偏好会受到信任用户的影响,因此利用信任用户l(l∈Mi)的特征向量更正用户i的特征向量,则更正后特征向量Pi为
(17)
将公式(17)以矩阵的形式表述,如公式(18)所示,其含义是将用户对其信任用户的信任值与原始的特征向量的乘积相加即得到更正后的特征向量。
(18)
假设用户间的综合信任度矩阵的向量Ti先验概率且服从高斯分布,则有
(19)
因此,用户特征向量在融入了综合信任度数据之后的概率分布为
(20)
利用贝叶斯推导,加入了综合信任度数据和概率矩阵分解的后验分布如下:
(21)
对公式(21)取对数并最大化得到最小损失函数,即得到最终目标函数。其计算公式如下:
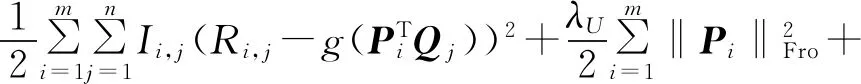

(22)


(23)
(24)
使用公式(25)和(26)迭代更新Pi和Qj,得到目标函数最小值。
(25)
(26)
式中:α为步长即学习速率,表示每次迭代时选取数据的变化大小。最后计算用户i对项目j的预测评分Ri,j:
(27)
本文的UPSA-PMF算法步骤的伪代码如下:
Input:ratings matrixR,user social matrixST,predicted score deviationγ,learning rateα,λU,λI,λT,nmin,nmax
Output:user latent feature matrixP,item latent feature matrixQ
1.{ fori=1 tomdo # step 1:calculate comprehensive trust
2. forj=1 tomdo
3. {rt←rt[i][j] # caclulate the user sim by formula(12)
4.st←st[i][j] # caclulate the user sim by formula(15)}
5. forj=1 tomdo
6. {T←T[i][j] # caclulate the user sim by formula(16)}
7.initalize latent feature matrix:P,Q~N(x|0,δ2)
# step 2:gradient descent
8.for (i,j) 9.returnP,Q 10.} 本文实验采用公开的Epinions数据集,包含了所需的用户评分数据和社交关系数据,其中包含了49 289名用户对139 738个项目的664 824条评分数据,以及487 183名用户之间的信任关系数据。用户的评分范围为1~5,用户之间的信任关系不对称。在本文实验中,采用五折交叉验证法进行验证[19],即随机选取Epinions数据集的80%数据作为训练集,剩下的20%作为测试集。 为了分析本文所提算法的优劣,采用平均绝对误差(Mean Absolute Error,MAE)和均方根误差(Root Mean Square Error,RMSE)作为评价预测评分准确性的评价指标,其定义如下: (27) (28) 式中:Γ表示测试集中的评分数据信息。将所有预测得到的分值与测试集中的真实分值进行比对,通过所得评分差值计算MAE和RMSE,其值越小,表示评分偏差越小,算法效果越好,准确率越高。 在本文的算法中,包含的参数有特征因子个数k、评分偏差阈值γ、迭代次数d、用户间的共同评分项目的最小个数nmin和最大个数nmax,以及正则化系数和学习速率。在本文中,为了减小算法复杂度的同时又不失一般性,将正则化系数设置为λU=λI=λT=0.001。对于学习速率α,由于该参数只影响算法取值的快慢,不影响算法结果,因此,将α设为1。 对于参数k,通常取值为5或10。在本文实验中,通过对比在不同迭代次数下的MAE和RMSE的变化情况来确定参数k,实验结果如图2所示。 (a)参数k对MAE的影响 (b)参数k对RMSE的影响图2 不同迭代次数下参数k对MAE、RMSE的影响 由图2可知,随着迭代次数的增加,MAE和RMSE的值不断减小;当参数k为5时,MAE和RMSE的值整体比k为10时的结果差,因此,选择参数k=10。 参数γ用来评估预测评分与真实评分的偏差多少为可靠,其值越小,对于评分数据的相似性越严苛,但也表明用户偏好越相似,评分越可靠。考虑到该值设置得过低会引入过多的干扰数据,影响推荐的结果,设置得过高将导致数据稀疏性越大,因此将γ设置在[0.9,1.5]进行实验,结果如图3所示。 (a)参数γ对MAE的影响 (b)参数γ对RMSE的影响图3 参数γ对MAE、RMSE的影响 从图3可以看出,在不同的迭代次数下,MAE和RMSE的趋势先减小后增大,当迭代次数为350时,γ=1.2时取得最优值,因此将参数γ设为1.2。 参数nmin和nmax用于调整最终的用户间信任度主要依赖于2.1节的信任度还是2.2节的信任度。参考文献[18]的实验,本文将nmin设置为0,然后将参数nmax设为{5,6,7,8,9,10}进行实验,结果如图4所示。 (a)参数nmax对MAE的影响 (b)参数nmax对RMSE的影响图4 参数nmax对MAE、RMSE的影响 从图4可以看出,随着迭代次数的增加,MAE和RMSE的值在降低,表明推荐的准确度在提升,并在nmax为5时整体的推荐效果最好,因此将参数nmax设为5。 为了验证本文算法的推荐质量,选择了4种推荐算法进行比对分析。 (1)PMF[5]:该算法只利用了评分信息。 (2)SoRec[6]:该算法将用户评分矩阵和社交关系矩阵同步分解,并通过共享的用户特征与概率矩阵因子模型相融合。 (3)SocialMF[7]:该算法假设目标用户的偏好受直连信任用户的影响,并作用在概率矩阵分解过程中的用户特征向量上。 (4)TrustMF[8]:该算法不仅把评分矩阵和关系矩阵同步分解,还把社交网络区分为信任和被信任关系,并把这两种关系结合到用户特征向量中。 为了验证本文在2.1节和2.2节改进的有效性,将对比实验分为两部分: (1)将2.1节基于用户偏好计算得到的信任度用于推荐算法中,并命名为UP-PMF算法,然后与结合2.1节和2.2节的算法UPSA-PMF进行比较,分别进行5组实验,验证2.2节改进的有效性; (2)将本文结合2.1节和2.2节的UPSA-PMF算法与上述算法进行比较,分别取5组实验的均值,验证本文所提算法的有效性。 对于第一部分的实验,其结果如图5和图6所示。在采用用户偏好计算用户间信任度时,结合使用社交活跃度计算用户间信任度的UPSA-PMF算法的RMSE和MAE明显比单独使用用户偏好计算用户间信任度的UP-PMF算法结果好,因此,证明了2.2节改进的有效性。 图5 UP-PMF和UPSA-PMF的MAE比较 图6 UP-PMF和UPSA-PMF的RMSE比较 对于第二部分的实验,结果如图7和图8所示。在指标MAE上,本文提出的UPSA-PMF算法相对于前四种对比算法分别降低了18.9%、11.97%、9.67%和4.9%;在指标RMSE上,本文提出的UPSA-PMF算法相对于前四种对比算法分别降低了11.9%、3.65%、1.79%、1.32%。根据对比图可以得出以下结论: 图7 不同推荐算法的MAE对比实验 图8 不同推荐算法的RMSE对比实验 (1) 和仅仅使用了评分数据的PMF算法相比,本文的UPSA-PMF算法的准确率有所提高; (2) 与SoRec和SocialMF算法相比,由于UPSA-PMF算法使用共同评分项目平衡因子和热门项目惩罚因子,改进了传统的相似度计算,使得能适应于具有不同评分数量的用户,提高了寻找近邻用户的准确度; (3) 与TrustMF算法相比,UPSA-PMF算法因为使用了社交活跃度对用户间的信任度进行了惩罚,使得用户间的信任度有所区分; (4) 由于本文的UPSA-PMF算法是从评分数据中的用户偏好以及社交网络中的社交活跃度的角度,能更加精确地刻画用户间的关系,因此具有更好的推荐效果。 本文根据用户偏好和社交活跃度,提出了一种融合用户偏好和社交活跃度的概率矩阵分解推荐算法。在根据用户偏好求信任度时,根据两个用户间共同已评项目数量占总共评分数量的比重来缓解用户项目评分数较少的情况,通过热门惩罚因子来修正用户间的相似度,能适应具有不同评分数量的用户,并减少评分数据的稀疏,然后根据评分偏差阈值计算用户间的信任度。在根据社交活跃度求信任时,考虑到社交好友与活跃度不高的用户的关系更牢固,因此把社交活跃度作为惩罚因子,得到更准确的信任度。最后将两种信任度结合,更精准地刻画了用户间的关系,从而提高了推荐精度。未来,可以从用户评分的时间信息考虑,将更多信息融入算法,以得到更精准的推荐准确度。3 实验分析
3.1 数据集
3.2 评价指标
3.3 参数调整
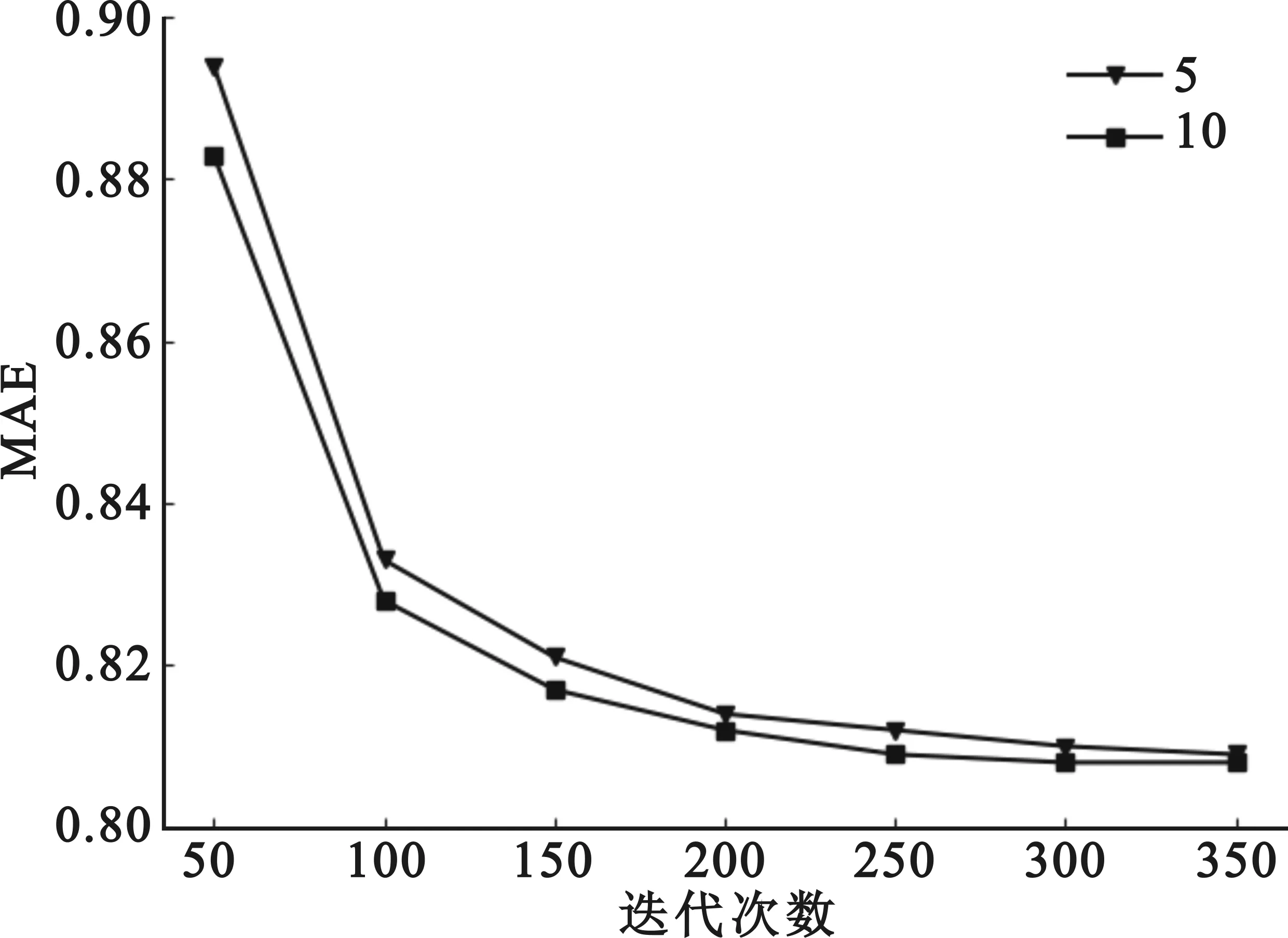




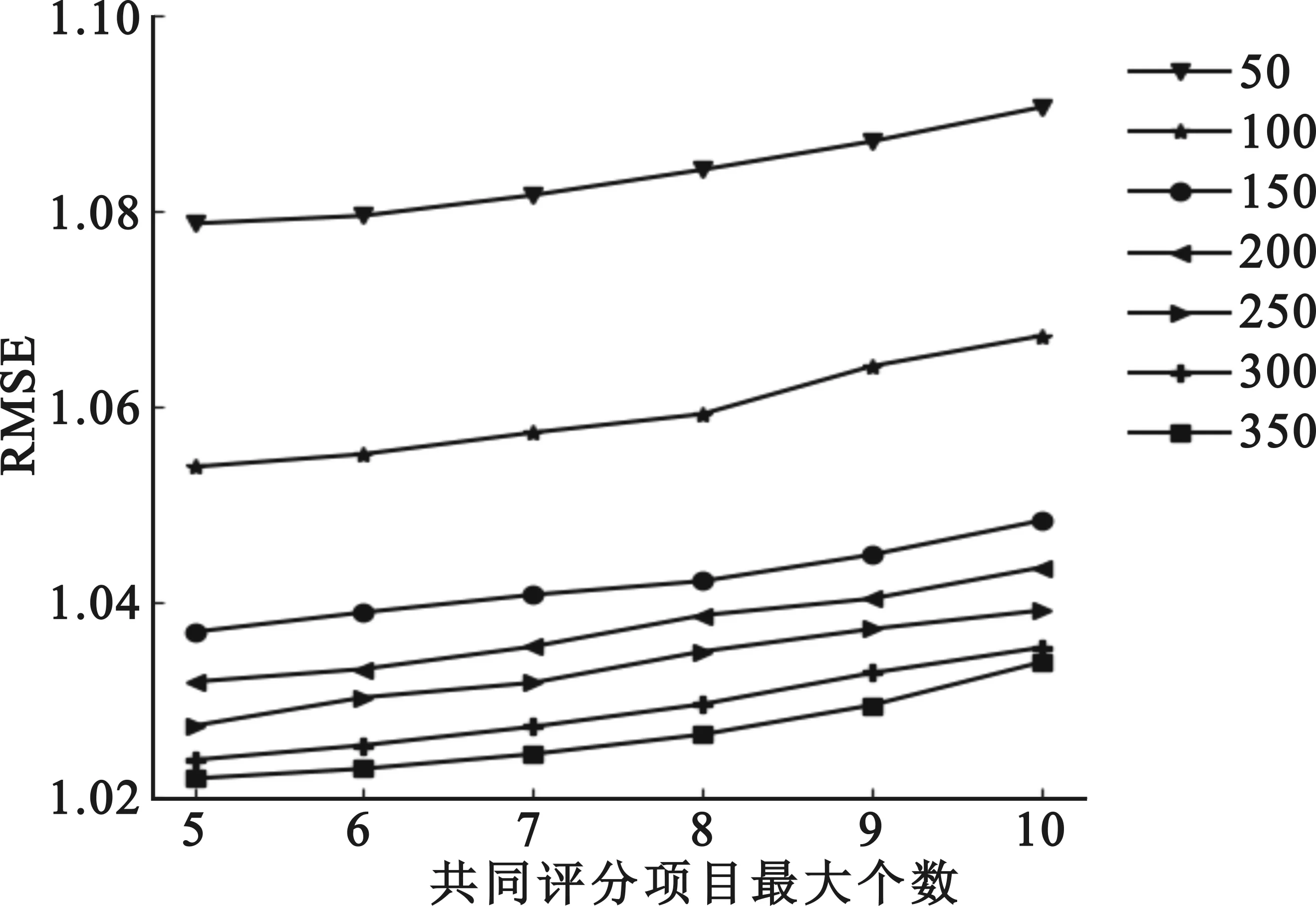
3.4 算法比对

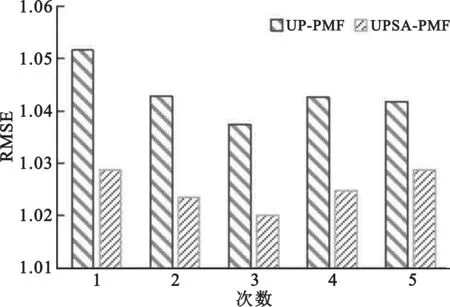
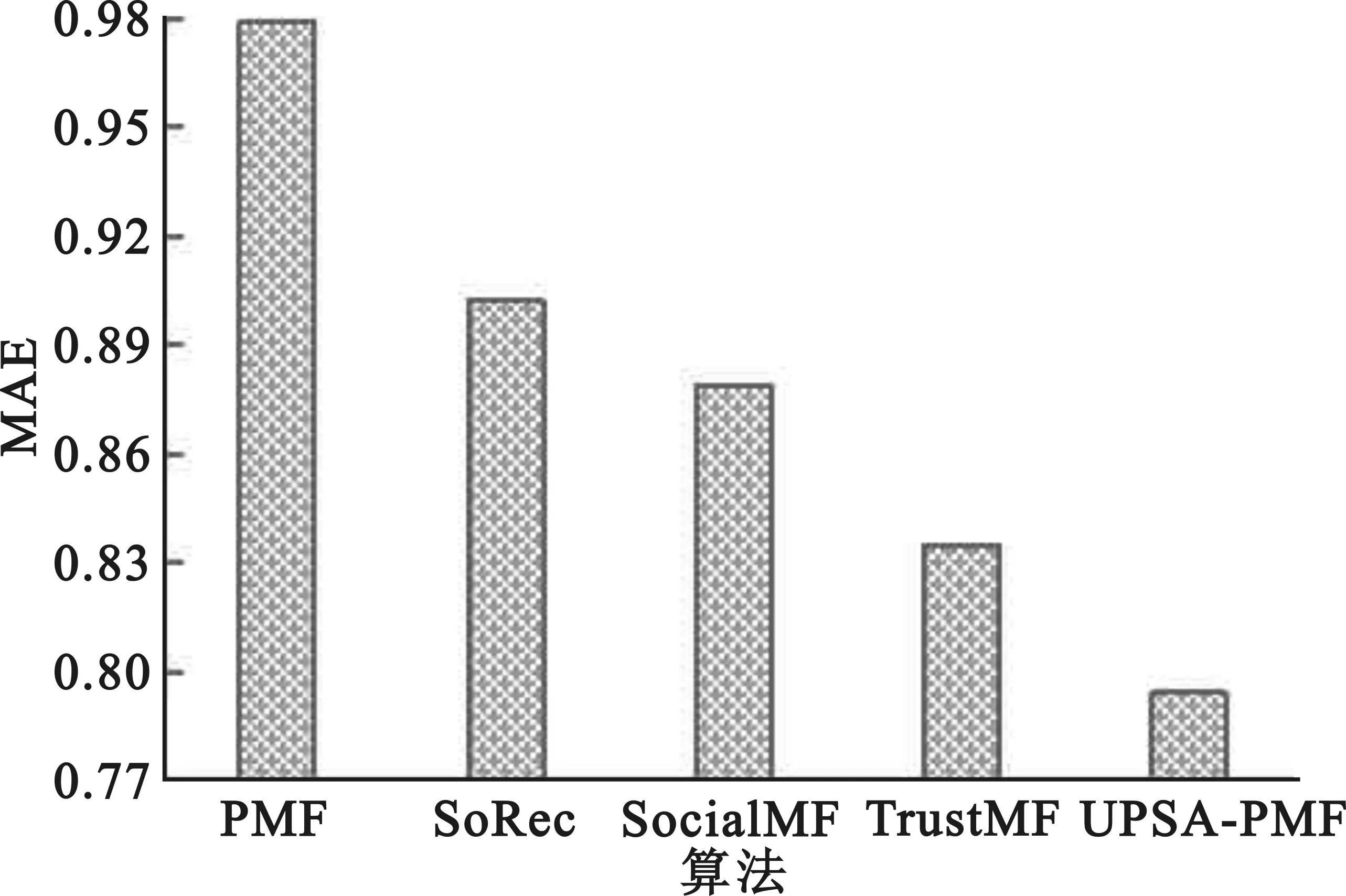

4 结束语
