一种抗频偏的定时同步方法及其性能分析 *

付博炜，李明齐

(1.中国科学院上海高等研究院，上海201210；2.上海科技大学 信息学院，上海 201210； 3.中国科学院大学，北京 100049)

0 引 言

在无线通信中，信号的同步至关重要。基于数据辅助的同步算法可以分为自相关定时同步算法和互相关定时同步算法两大类[1]。

自相关定时同步算法的核心思想是在发送端发送特定的训练序列(多段重复或共轭对称的结构)，在接收端对接收数据做延时自相关运算。通过自相关结果对信号的起始位置和载波频偏进行估计，实现简单，在信噪比较高的情况下表现良好[2-3]。但由于自相关算法定时包络不尖锐，而且相关的两段辅助数据都会受到信道噪声的干扰，自相关在低信噪比的情况下性能较差。

互相关定时同步算法的核心思想是在本地保存一份发送训练序列，通过接收数据与本地序列做互相关运算。与自相关同步算法相比，互相关算法定时包络尖锐，而且本地序列没有受到噪声和信道的影响，定时偏差小，适用于低信噪比的环境[4-7]。但互相关算法对载波频偏敏感，随着载波频偏的增加性能会迅速下降。文献[8]对互相关同步中载波频偏的影响作了分析，通过限制训练序列长度来减少载波频偏的影响，但减少训练序列长度同样会降低定时同步的性能。文献[9-10]通过粗频偏估计的方法估计出载波频偏，补偿后进行细定时同步，该方法实现复杂度较高，需要额外的处理时延，而且同步性能受粗频偏估计性能影响，只适用于短序列，信噪比较高的情况。文献[11]提出了分段互相关的算法，将互相关运算分段进行以减少载波频偏带来的衰减，最后取绝对值相加得到同步判决度量。尽管该算法实现简单并在实际系统中得到了应用，但分段绝对值的做法同时会放大噪声的均值，增加接收机虚警的概率。

本文首先对载波频偏的影响和传统的分段互相关算法性能进行分析，在此基础上提出了一种分段频偏补偿的算法，在传统分段算法的基础上，以频偏补偿代替绝对值操作。理论分析和仿真结果表明，在大频偏的情况下，改进方法的同步性能要优于传统分段算法。

1 互相关同步和载波频偏影响

在加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道下，对于发送长度为N的训练序列s(n),接收机接收到的信号为

r(n)=s(n)ej2πεn/N+w(n)。

(1)

定义ε=df/(fs/N)为归一化载波频偏，其中fs为采样率，df为载波频偏；w(n)为方差为σ2的加性高斯白噪声。接收信号与本地序列的互相关结果为

(2)

得到归一化定时同步判决度量为

(3)

不失一般性，假设发射信号和接收信号的功率为1。在同步时刻，同步判决度量为

(4)

M(0)=|αN+w′|。

(5)

式中：α为频偏衰减系数，

(6)

当ε<0.5时，通过二阶泰勒展开可以近似为α=1-π2ε2/6，互相关峰值会随着载波频偏的增加而迅速变小，从而降低定时同步的性能。

接收信号的定时同步可以看作一个检测判决问题：

(7)

式中：H1为正确同步假设，判决度量为互相关峰值与等效噪声之和；H0为错误同步假设，判决度量为等效噪声。当n=0时，M(n)服从莱斯分布，在互相关峰值αN远大于噪声功率σ2时，M(0)可以近似为均值为αN、方差为Nσ2/2的正态分布；当n≠0时，M(n)为方差为σ2复高斯噪声的包络，服从瑞利分布。

定义同步检测概率为PD,虚警概率为PFA,根据奈曼-皮尔逊(Neyman-Pearson)引理，令判决门限为thr,则互相关同步算法的检测概率为

(8)

虚警概率为

(9)

检测概率和虚警概率的关系为

(10)

式中：Φ为标准正态分布的概率分布函数。从式(10)中可以看出，在虚警概率确定的情况下，互相关同步性能只与训练序列长度、噪声功率和载波频偏有关，载波频偏的增加会导致同步检测概率的下降。

2 分段算法和性能分析

文献[11]提出了一种分段算法，通过分段取绝对值的操作降低了载波频偏的影响，将互相关运算分为L段，在n=0时，同步判决度量为

(11)

(12)

同步检测概率可以近似为

(13)

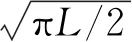
3 改进的分段频偏补偿算法和性能分析

在互相关同步算法中，频偏可以通过每段互相关的相位差求得：

(14)

式中：Pi(n)是每小段互相关的结果，

(15)

频偏估计的结果可以近似为

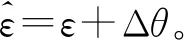
(16)

频偏估计误差Δθ服从均值为0、方差为L2σ4/(4(L-1)3π2N2)的正态分布[12]。相比于定时同步，频偏估计的结果受噪声影响更小，结果更为准确。改进的频偏补偿算法的定时同步度量为

(17)

由于Δθ较小，若N>>σ2，在n=0时，Mpro(n)可以近似为均值为N(1-π2ε2/6L2)、方差为Nσ2/2的正态分布的随机变量;当n≠0时，由于频偏补偿不改变同步结果的幅值，噪声仍可以看作L段均值为0、方差为Nσ2/L的高斯噪声wl的叠加：

(18)

式中：

(19)

图1 改进算法等效噪声均值随分段次数L的变化

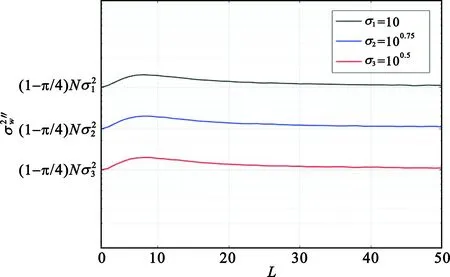
图2 改进算法等效噪声方差随分段次数L的变化

改进算法的虚警概率近似为

(21)

改进算法的同步检测概率为

(22)

在低信噪比、大频偏的场景中，改进算法的性能要优于传统的分段算法。

4 实现复杂度分析

将长度为N、分段次数为L的传统分段算法和改进分段算法的实现复杂度进行简要分析，结果如表1所示。

表1 算法实现复杂度

在传统分段算法中，频偏估计在完成定时后进行，式(14)用于计算频偏的三角函数模块可以复用。而改进分段算法需要即时地计算出频偏，并且对相关峰进行频偏补偿，频偏估计中的三角函数模块不能复用。但在序列长度N较大、分段次数L较小的情况下，改进分段算法增加的运算只占系统总运算量中很小的一部分，改进分段算法与传统分段算法的实现复杂度相近。

相比于文献[10]中的频偏补偿算法，改进算法不需要进行粗同步，频偏估计结果可以在计算出互相关后即时得到，频偏补偿只需要对少量相关峰进行，无需额外的迭代运算，计算复杂度低，内存占用少，适合在实际工程中实现。

5 性能仿真与分析

为验证理论分析结果，将分段互相关同步和本文提出的改进算法的定时同步性能进行仿真和对比。测试采用正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)系统，载波频率为fc=600 MHz,子载波间隔为3.75 kHz，同步训练序列长度为N=4 096，以虚警概率PFA=10-3确定同步判决门限。在实际实现中，算法的实现复杂度会随着分段次数L的增加而增加，当L=N时，算法的实现复杂度与文献[10]中的频偏补偿算法相当。改进算法的分段次数不宜过大，在实现中可以根据接收信号的最大频偏选择合适的分段次数。

首先对理论分析结果进行验证。图3给出了改进算法式(22)中理论分析与实际仿真在不同频偏下的AWGN信道下的定时同步性能。由于频偏估计误差和近似误差的存在，算法实际性能略低于理论分析性能。从L=2到L=8，由于等效噪声的方差有所增加，导致改进分段算法的同步检测概率随着分段次数L的增加而下降，但下降幅度较小。改进算法在分段次数较多的情况下仍然能够保持较好的同步检测性能。

图3 AWGN信道下改进算法理论性能和实际性能的比较

图4为相同虚警概率的情况下传统分段算法和改进算法的定时同步性能。从仿真结果可以看出，一方面在没有频偏的情况下，不进行分段的互相关算法同步性能最好。无论是绝对值算法还是改进算法的同步性能都会随着分段次数L的增加而有所下降。但相比于分段绝对值算法，改进算法由于分段造成的性能损失较小，在相同分段次数的情况下，改进算法的同步性能要优于绝对值算法。另一方面，随着分段次数L的增加，系统的抗频偏能力会得到增强，在大频偏的情况下，分段带来的抗频偏增益要大于分段带来的性能损失。改进算法可以通过增加更多的分段来获得更强的抗频偏能力。

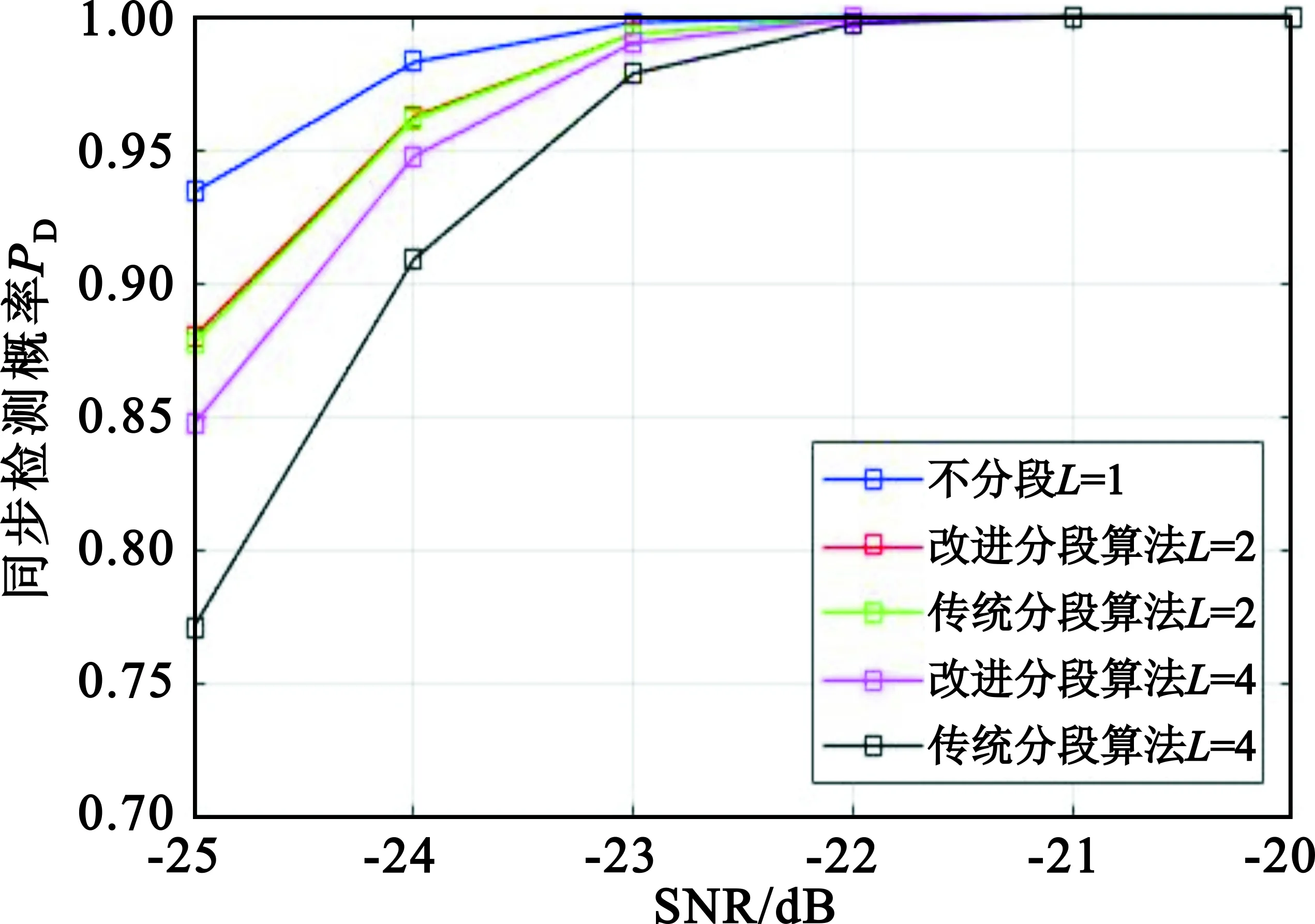
(a)归一化频偏ε=0

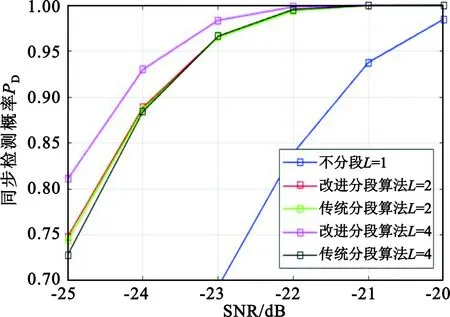
(b)归一化频偏ε=0.5图4 AWGN信道下改进分段算法和传统分段算法同步性能的比较

在多径信道下，同步检测算法主要是对最强径(往往是第一径)进行同步检测和估计，AWGN信道下分析的改进算法可以推广到多径信道中。图5为两径莱斯信道下改进算法和分段算法的仿真结果,信道第一径和第二径的增益分别为0 dB、-3 dB，莱斯因子为10，第二径时延为2 μs。从仿真结果中可以看出，在多径信道下，相同分段次数的改进算法的性能仍优于传统的分段算法。

(a)归一化频偏ε=0

(b)归一化频偏ε=0.5图5 多径信道下改进分段算法和传统分段算法同步性能的比较

6 结 论

本文对频偏对互相关同步性能的影响以及传统分段互相关同步的性能进行了分析。针对传统分段互相关算法同步算法在低信噪比的情况下性能随着分段次数增加而迅速下降的问题，提出了一种改进的分段频偏补偿互相关同步算法。理论分析和数值仿真表明，本文所提算法的同步性能要优于传统分段互相关算法，适用于低信噪比、高频偏的通信系统，具有很好的实用价值。