面向LEO卫星网络的高效路由算法 *
2021-07-02雷援杰马枢清
雷援杰 ,唐 宏,马枢清,李 艺
(重庆邮电大学 a.通信与信息工程学院;b.移动通信技术重庆市重点实验室,重庆 400065)
0 引 言
随着通信技术的发展,天地一体化网络已成为下一代通信的发展趋势。作为天基骨干网络的低轨(Low Earth Orbit,LEO)卫星网络因为具有全球覆盖、可以忽略地形限制进行点对点通信等优点而成为研究的热点[1]。
LEO卫星网络具有时变的动态拓扑特征,这是不能直接将地面网络路由算法直接迁移到卫星网络上的主要原因[2]。随着SpaceX的starlink计划的推进[3],卫星组网规模变得更加庞大,成为未来卫星网络发展的一种趋势,但是卫星星上存储以及计算能力有限[4],所以高效简洁的路由算法成为卫星网络的一个研究重点。
卫星路由是卫星通信中的核心。针对该问题,DT-DVTR(Discrete Time Dynamic Virtual Topology Routing)算法[5]利用快照的思想,将卫星随时间连续变化的动态网络拓扑结构离散化,并且在每个快照内近似认为网络拓扑结构是静止不变的,然后将在线下利用Dijkstra算法寻找出的最短路径存储在卫星上,当有数据转发需求时,查询路由表完成数据转发。但是该算法并没有应对突发流量的能力。文献[6-7]通过对服务质量(Quality of Service,QoS)指标进行最优化建模,通过蚁群算法计算出满足多种QoS约束的最优路径。尽管蚁群算法能够求解出一条或者多条满足QoS指标的路径,但是相对于传统算法,计算复杂度相对较高。
最短路径算法是表驱动路由中的重要组成部分。广度优先搜索(Breadth First Search,BFS)算法可以解决无权图的最短路径问题。Dijkstra算法拥有较低的复杂度,但是不能处理负权边问题。Bellman-Ford算法可以解决负权边的最短路径问题,却拥有相对较高的时间复杂度[8]。随着启发式算法的发展,一些仿生优化算法也常被应用到寻找带约束条件的最优路径中。文献[9]将路径距离作为蚁群算法的启发式因子从而计算出蚂蚁移动到相邻下一跳的转移概率,最后通过信息素浓度选出满足约束条件的最优路径。文献[10]将待选路径编码成可变长度的字符串,将路径的权值和作为适应度函数,利用遗传算法寻找最优路径。启发式算法的优点在于能够寻找拥有约束条件的最优路径,但是其时间复杂度一般比传统的最短路径算法高。
本文提出一种基于BFS的最优路径算法en-BFS(Enhance Breadth First Search),将跳数作为最优路径的主要衡量指标寻找出最小跳数路径集合,然后通过在最小跳数集合中筛选出权值和最小的路径作为目标路径完成数据的转发,极大地降低了路由算法复杂度以及卫星的计算资源。为了克服en-BFS算法在网络负载较轻时时延相对偏大的缺点,提出了NCARA(Network Congestion-Aware Routing Algorithm)路由策略,即在路由时,节点会感知网络拥塞程度,当网络处于非拥塞状态时,采用Dijkstra算法寻路;当网络拥塞时,采用en-BFS算法寻路,使得网络性能能够得到保障。
1 系统模型
本文的研究对象为极轨道卫星星座,并且将网络建模为G=(V,E),V=N×M表示当前卫星星座中有N个轨道到平面,每个轨道平面有M颗卫星。为了方便后续的叙述,每个节点v用(xv,yv)来表示该节点是第xv轨道平面的第yv颗卫星。并且对于极轨道卫星星座而言,每颗卫星可以建立4条星间链路,包括不同轨道平面相邻卫星之间建立的2条轨道间链路以及相同轨道平面相邻卫星之间建立的2条轨道内链路。在第一个轨道平面与最后一个轨道平面以及处于极地区域的相邻轨道的卫星之间,由于卫星相对运动速度过快,故一般不存在轨道间链路。所以,由于卫星周期性地进出极地区域,会导致卫星轨道间链路周期性地断开与连接,从而使得卫星网络拓扑拥有动态变化的特征。
为了屏蔽卫星拓扑变化的动态性,本文采用虚拟拓扑策略,将卫星连续变化的动态拓扑通过采样的方式抽象成n个离散的时间片,只要相邻时间片的间隔Δt足够小,便可以认为每个时间片内的拓扑是静止不变的。所以在每个快照范围内,节点可以近似抽象为一个二维网格拓扑。
2 算法总体架构
为了在降低寻路算法复杂度的同时保证网络性能,本文提出一种针对网络的拥塞情况选择不同的寻路算法寻路的路由策略——NCARA。
NCARA的基本思想如下:在每个节点泛洪自身信息的时候,会将该节点的拥塞情况泛洪出去,节点拥塞情况可以利用该节点的待处理数据队列长度进行判断。设定阈值β,当队列长度大于β时判定该节点处于拥塞状态,否则该节点为非拥塞节点。并且在每个节点收集网络拓扑信息的时候,会统计拥塞节点总数,并根据拥塞节点总数来选择不同的寻路算法。设定阈值β1和β2,当拥塞节点总数小于β1时,采用Dijkstra算法寻路;当拥塞节点总数大于β2时采用后文将要介绍的en-BFS算法寻路,并且β1>β2。一般β1和β2应取不同值,主要是防止以下情况发生:假设网络选取阈值一样,则可能出现网络的拥塞节点个数一直在所选取的阈值处波动的情况,从而造成频繁的选路算法切换。
3 en-BFS算法
3.1 en-BFS算法总体思想
en-BFS算法主要由两部分组成,即寻找最小跳数路径集和寻找最小权值路径。寻找最小跳数路径集可以通过推导出最小跳数路径的节点所被包含的范围完成,然后在最小跳数路径集中通过加上松弛操作的BFS算法寻找权值和最小的路径。
本文使用的术语定义如下:
定义1:最小跳数路径集为从源节点src到目的节点dst的跳数和最小的路径集合,即满足
(1)
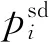
定义2:最小权值路径表示在源节点到目的节点的最条跳数路径集中权值和最小的路径,并且满足
(2)
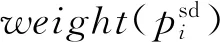
3.2 寻找最小跳数路径集
定理1:组成最小跳数路径集的每一条路径的每个节点一定包含在源节点到目的节点的最小矩形内,即满足v∈pi,pi∈mhopsetsd→xsrc≤xv≤xdes且ysrc≤yv≤ydes。
证明:如图1所示,假设a是源节点,b是目的节点,p1={a,d,e,f,g}是矩形外的一条路径,p2={a,b,c}是矩形内的一条路径。由于网络拓扑为一个二维网格拓扑,并且假设hop(v1,v2)表示从节点v1到v2的跳数,故hop(a,b)=hop(d,e),且hop(b,c)=hop(f,g),可得出hop(p1)>hop(p2)。除此之外,矩形外路径也可以提前到达矩形区域内节点,然后由矩形内区域的节点到达目的节点,证明过程和上面一样。
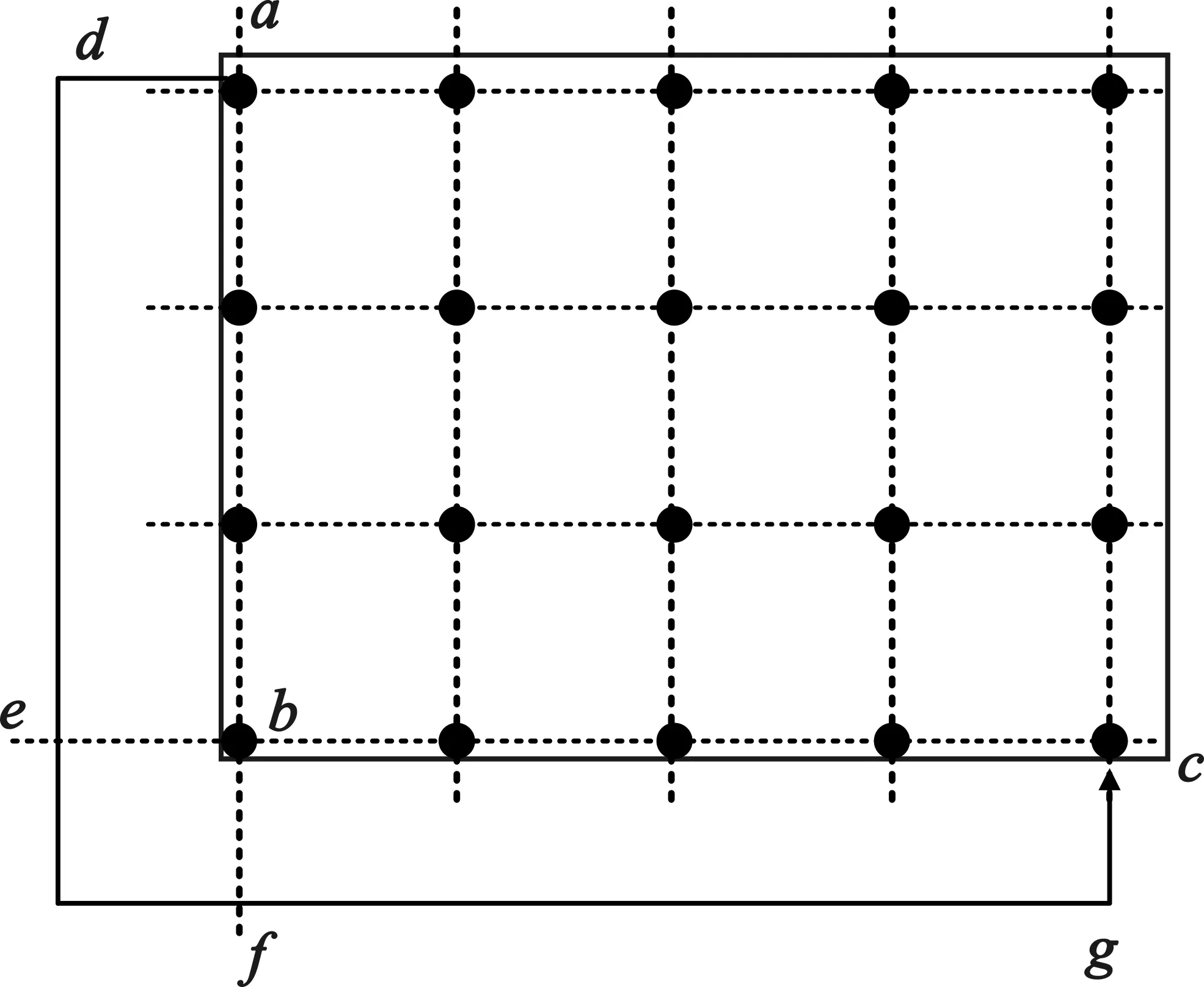
图1 最小跳数路径集范围证明
定理2:假设节点v和节点w为从源节点src到目的节点dst的一条最小跳数路径上的两个节点,并且节点w为节点v的后继节点,则节点w一定是在相对于v朝目的节点靠拢的方向。可用数学语言描述如下:
xw=xv且(yv-yw)·(ysrc-ydst)≥0,
或者
yw=yv且(xv-xw)·(xsrc-xdst)≥0。
3.3 寻找最小权值路径
由定理1可知,最小跳数路径一定是在包含源节点和目的节点最小矩形中,然后可以在该矩形范围内采用en-BFS算法寻找权值最小的路径。为了方便,本文权值采用传输时延和传播时延的加和,如公式(3)所示:
weight=α1Pt+α2Qt。
(3)
式中:weight表示寻找路径时的权值;Pt表示传播时延;Qt表示传输时延;α1和α2分别表示传输时延和传播时延的权重因子,一般α1和α2都取0.5。
3.3.1 en-BFS算法需用符号说明
接下来定义en-BFS算法需要用到的符号。定义集合Q,v∈Q表示v已经找到最短路径;反之,表示v没有找到最短路径。并且节点w为节点v的后继节点,v为w的前驱节点,pre(v)用来记录从源节点到v的最短路径中的上一跳节点,dis(v)表示从源节点到v的最短距离,weight(v,w)表示节点v和w的边的权值,队列queue用来模拟BFS的遍历过程,s代表源节点。
3.3.2 en-BFS算法具体步骤
en-BFS算法的具体步骤如下:
Step1 先将dis数组中所有值初始化为无穷大并且将源节点s加入队列queue以及已访问集合Q中,标记该节点的最优路径已经找到。将从源节点s到该节点的最短距离dis(s)置为0,s的上一跳pre(s)置为s。
Step2 取出queue中的第一个元素v,并且将它加入已访问集合Q中,进入Step 3。
Step3 将节点v的后继节点w加入队列queue的过程中判断节点w是否可以通过节点v进行转接使得源节点到w的距离更小,即判断dis(w)>dis(v)+weight(v,w)是否成立,如果成立进入Step 4,否者进入Step 5。
Step4 令dis(w)=dis(v)+weight(v,w),并且将w的上一跳置为v,即pre(w)=v。
Step5 判断所有节点是否全部都已经加入到已访问集合queue中,如果条件不满足执行Step 2,否则算法结束。
3.3.3 en-BFS算法伪代码
en-BFS算法的伪代码如下:
for eachv∈Gdo
pre(v)←0
dis(v)←∞
visited(v)←false
pre(s)←s
dis(s)←0
queue.add(s)
while queue is not empty do
v←queue.removefirst
visited.add(v)
for eachw∈ adj(v) do
ifw∉ visited then
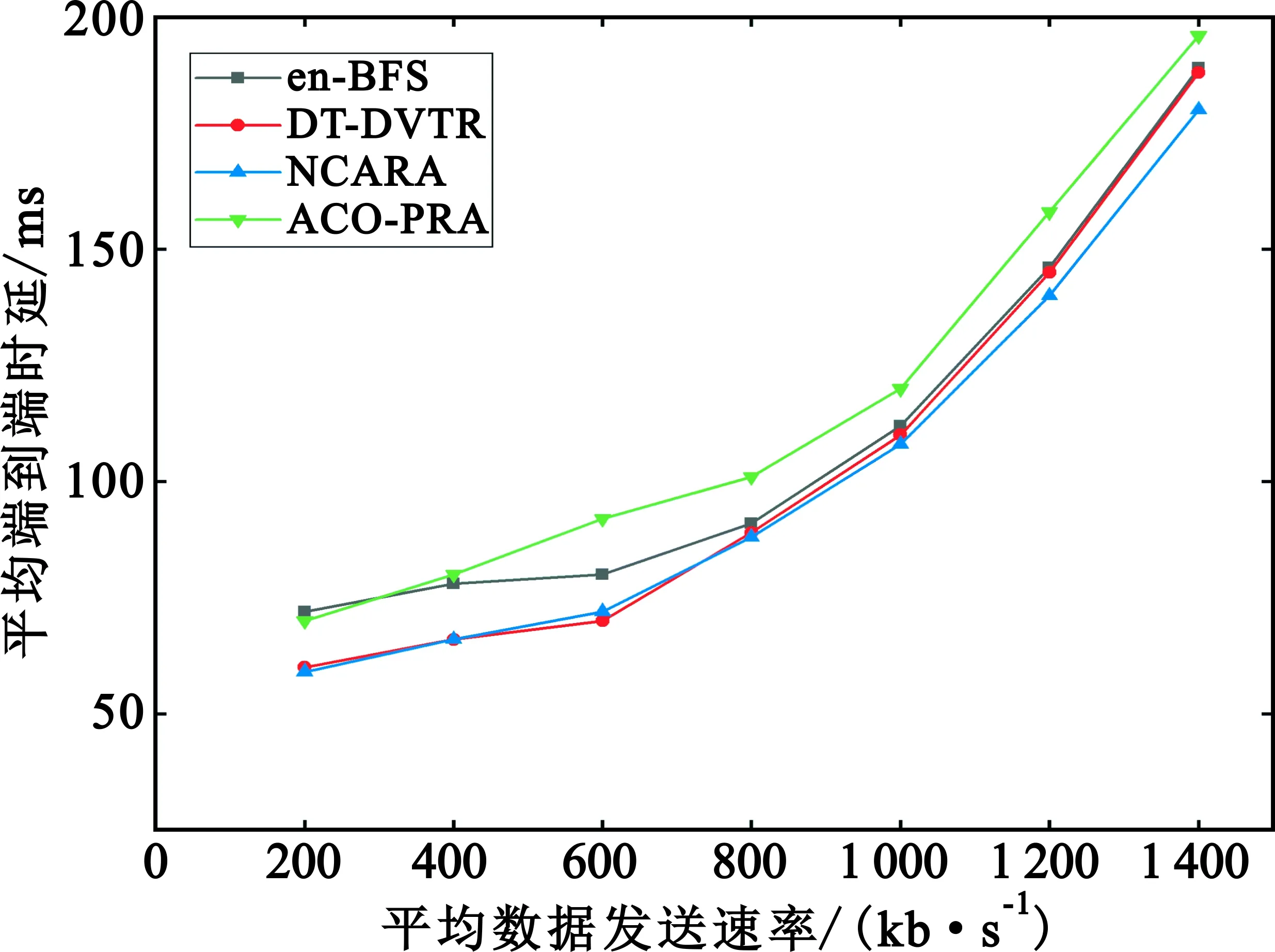
if dis(v)+weight(v,w) dis(w)←dis(v)+weight(v,w) pre(w)←v 3.3.4 en-BFS算法正确性分析 定理3:在包含源节点和目的节点的最小矩形范围内用en-BFS算法寻找到的路径一定是最小跳数路径集中权值和最小的路径。 证明:首先证明所寻路径一定是最小跳数路径。由BFS可以寻找无权图的最短路径可知,通过BFS对图进行广度优先遍历寻找到的路径一定是无权图中的最短路径,也即最小跳数路径。 接下来证明所寻路径一定是权值和最小的路径。如图2所示,假设源节点src在目的节点dst的左上方,由定理2可知对于最小跳数路径中的每一个节点的上一跳一定是在它的左方或者它的右方。 图2 en-BFS遍历层次图 图2中,l1表示搜索的第一层,l2为第二层,依次类推。利用数学归纳法可知: (1)当搜索层次n=1时,从源节点到该节点v只有一条边,即为最短路径; (2)当n=k时,假设该搜索层lk上的任意一个节点所寻找到的路径都为最短路径,如图2所示,便有dis(v1)和dis(v2)都是源节点到该节点的距离最小值; (3)当n=k+1时,任取lk+1上的节点w,并且w的上一跳一定是它的左方节点v1或者它的上方节点v2,由于dis(w)=min{(dis(v1)+weight(v1,w)),((dis(v2)+weight(v2,w)},故对于节点w寻找到的路径也一定是权值和最小的路径。 综上,算法正确性证明完毕。 3.3.5 en-BFS算法复杂度分析 由于en-BFS算法的核心思想是广度优先搜索算法,即遍历图中的所有边和所有的点,故en-BFS的时间复杂度为O(V+E),V为图的节点个数,E为图的边的数目。 表1是常用的寻找最短路径算法的复杂度,可以看出Dijkstra算法是和Bellman-Ford算法的时间复杂度都约等于O(V2),而蚁群算法的复杂度和蚂蚁数量m以及迭代次数T有关,但是它至少也是一个复杂度为O(V2)的算法。 表1 算法复杂度对比 综上,本文算法为一个线性复杂度的算法,并且相比Dijkstra算法以及传统的最短路径算法其复杂度都有明显降低。 本文采用卫星工具包(Satellite Tool Kit,STK)模拟生成铱星系统的轨道参数,然后导入到OPNET中,通过在OPNET中的网络域、节点域、进程域编程实现网络仿真[11]。 在铱星系统中,一共有6个轨道平面,每个轨道平面上有12颗卫星,轨道高度为780 km,每颗卫星有4条星间链路(第一个轨道平面和最后一个轨道平面的卫星以及极区内卫星除外)。由于天线原因,第一个轨道平面和最后一个轨道平面之间不存在轨道间链路,同时极区内卫星之间不存在轨道间链路,仿真设置极区边界值为70°。为了方便研究,卫星系统的轨道倾角设置为90°。为了屏蔽卫星网络拓扑的动态性,本文采用虚拟拓扑的方式。由于全文对比算法都是表驱动路由的形式,故设置更新路由表的时间间隔为10 s。表2是仿真所用卫星系统的参数。 表2 仿真参数设置 本文中卫星的轨道间链路和轨道内链路带宽都设置为1 Mb/s,每个卫星节点的等待队列长度为100 Mb,并且设定β为75 Mb,当节点的队列长度超过β时便判定该节点为拥塞节点,并且当节点队列中的数据包总比特数超过队列总长度100 Mb时便丢弃该数据包。β1设置为36,β2设置为30,当卫星拥塞节点个数小于36时采用Dijkstra算法寻找最短路径,当拥塞节点个数大于30时采用en-BFS算法寻路。 在仿真实验中,我们选取了DT-DVTR、ACO-PRA等典型卫星网络路由算法和本文的en-BFS算法以及NCARA算法进行比较。其中DT-DVTR采用Dijkstra算法寻找最短路径,而ACO-PRA采用的寻路算法是蚁群算法。 本文中设定数据包的到达时间间隔服从指数分布,从而可以通过控制仿真中指数分布的平均值来控制平均数据发送速率。 4.2.1 平均跳数 网络平均跳数如图3所示,可见随着平均数据发送速率的增大,en-BFS算法的跳数一直处于稳定状态并且优于其他三种算法,原因是en-BFS算法将跳数作为主要衡量指标,故它寻找的每条路径都是最小跳数路径。PRA-ACO算法将跳数作为QoS的衡量指标,故在数据发送速率较小时比以DT-DVTR的平均跳数略低。而DT-DVTR算法采用Dijkstra算法作为寻路算法,衡量指标为传播时延和传输时延,在网络非拥塞时,传播时延作为主要的衡量指标,故寻找的最短路径不一定是最小跳数路径。随着平均发送速率的增大,网络处于拥塞状态,此时传输时延在衡量指标中权重加大,故此时最短路径近似等价为最小跳数路径,此时DT-DVTR算法和en-BFS算法都趋于寻找最小跳数路径,故平均跳数趋于稳定。NCARA算法前面采用Dijkstra算法,后面采用en-BFS算法,故平均跳数和DT-DVTR算法近似保持一致。 图3 路由算法平均跳数对比 4.2.2 平均端到端时延 图4所示为平均端到端时延,可以看出ACO-PRA算法由于考虑多种QoS因素,平均端到端时延略高于其他三种算法。en-BFS算法在平均发送速率较低即网络拥塞程度较低的时候,其主要衡量指标为跳数,故寻找到的路径可能不是最优路径,导致平均端到端时延略大于DT-DVTR算法。NCARA算法在网络处于非拥塞时采用Dijkstra算法,而在拥塞时采用en-BFS算法,故它的平均端到端时延和DT-DVTR算法的平均端到端时延近乎一致。 图4 路由算法平均端到端时延对比 4.2.3 平均丢包率 平均丢包率如图5所示。由于在仿真时设置了节点的队列长度,并且当节点的队列数据包比特数超过队列长度的时候,便会丢弃数据包,这是造成丢包的主要原因。并且由于本文算法为表驱动路由,故也有可能由于节点在传输数据包时由于星间链路断开,但是更新路由表不及时,从而导致丢包。 图5 路由算法平均丢包率对比 由于ACO-PRA算法将丢包率也作为一个QoS因子进行路径计算,所以它的丢包虑相对较低。en-BFS算法寻找的路径为最小跳数路径,所以其因为轨道间链路断开而丢包的概率应该略低于其他两种算法。NCARA算法和DT-DVTR所寻找的路径在随着平均数据发送速率增大都是近乎一样,故丢包率也近似一样。 本文针对低轨卫星网络呈二维网格拓扑的特征,提出了一种en-BFS算法。该算法以跳数作为主要衡量指标寻找出最小跳数路径集,然后以传输时延和传播时延作为链路权值,通过en-BFS算法寻找出权值和最小的路径。由仿真可知,当网络处于拥塞时,采用en-BFS算法和DT-DVTR算法中采用Dijkstra算法寻找的路径近乎是一样的,但是传输时延却高于DT-DVTR算法,于是提出了基于网络拥塞程度感知的路由算法(NCARA)。该算法设置了网络拥塞阈值,当网络拥塞程度高于拥塞阈值时采用en-BFS算法寻路,当网络拥塞程度低于拥塞阈值时采用Dijkstra算法寻路,这样该算法寻找到的最短路径便和DT-DVTR采用Dijkstra算法寻找到的最短路径近乎一样。由仿真可知,NCARA和DT-DVTR算法性能差不多,但是在算法复杂度上,NCARA在网络拥塞时采用的en-BFS算法是一个O(V+E)时间复杂度的算法,优于其他寻路算法。所以本文在没有牺牲网络性能的前提下降低了算法复杂度。 为了解决网络负载不均衡问题,下一步将增加负载均衡策略,达到网络负载均衡的目的。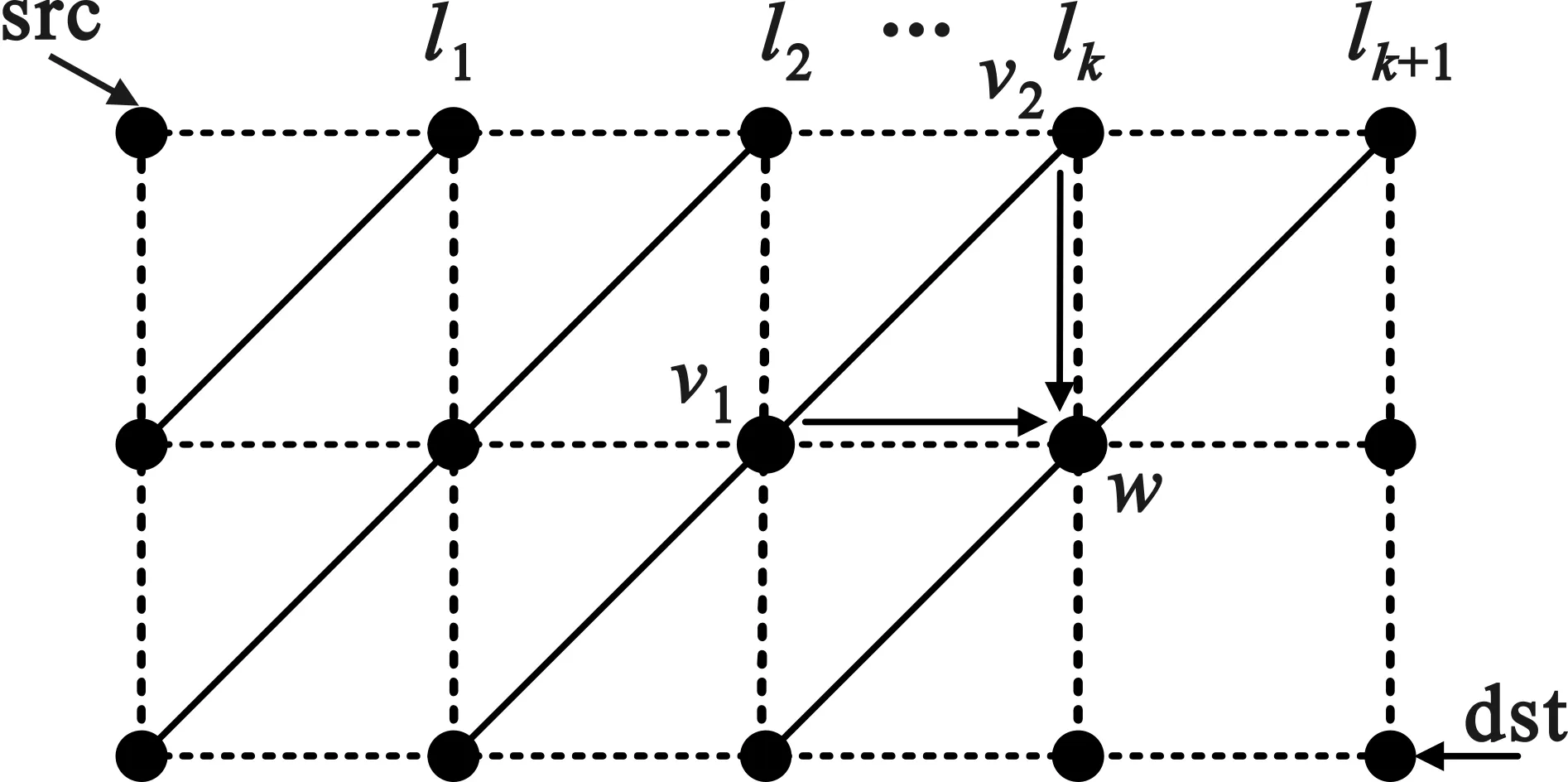

4 仿真分析
4.1 仿真建立
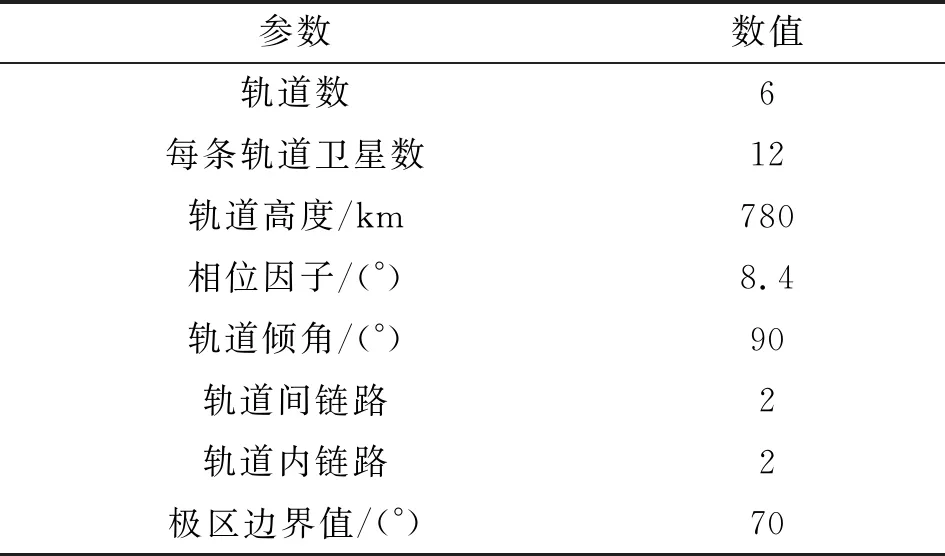
4.2 仿真结果分析


5 结束语
