基于多核处理器BWDSP1042的FFT性能优化 *

蔺丽华，李 敏 ，苏 涛，张美春，王佳仪

(1.西安科技大学 通信与信息工程学院，西安 710054；2.西安电子科技大学 雷达信号处理国家重点实验室，西安 710126)

0 引 言

快速傅里叶变换(Fast Fourier Transform，FFT)广泛应用于信号、音频、图像等领域的科学计算与处理，是这些领域时频转换的基本研究工具[1]。FFT算法性能的优劣代表着DSP芯片处理能力的高低，FFT运算时间作为表征芯片性能的重要参数，各领域对于FFT计算与处理的实时性要求也越来越高[1-2]。

为响应国家大力发展国内集成电路产业的号召，打破国外的高计算性能领域的核心技术对我国的垄断，中国电科38所自主研发了一款具有自主知识产权的BWDSP产品。BWDSP1042[3]是一款运算速度快、功耗低、实时性强、便携的高性能双核DSP，又名“魂芯二号“，其底层架构、指令集和集成开发环境ECS都是38所自主设计与研发的。BWDSP1042是在第一代产品BWDSP100[4]的基础上所开发的，仍然是16条发射超长指令字(Very Long Instruction Word，VLIW)和4路单指令流多数据流(Single Instruction Multiple Data，SIMD)混合架构的数字信号处理器，但内核升级为eC104+，扩展了指令集，优化了存储空间，执行部件提升了运算性能，在物理存储空间上划分了程序空间和数据空间。

本文基于BWDSP1042的体系结构和指令编排，在开发环境ECS下完成FFT带有C程序调用接口的汇编程序，基于按时间抽选的基-2 FFT[5]算法进行结构优化，通过多阶合并、指令并行、循环展开、软件流水和高效寻址指令等方式进行并行计算，使用汇编程序的实际运行周期来衡量算法优化程度，并与BWDSP100和TMS320C6678函数库中的FFT做对比，使用Matlab程序验证本文汇编程序的正确性，按照误差阈值来判定FFT算法功能编写是否准确。研究结果表明，512点、1 024点、2 048点定点复数FFT算法的实际运行周期分别为571、991、2 112，比BWDSP100函数库中的FFT分别提升了1.12倍、1.18倍、1.27倍，比C6678函数库中的FFT分别提升了1.32倍、1.40倍、1.88倍。本文研究的基于BWDSP1042的FFT算法计算速度快，实时性高，对支持国产芯片BWDSP1042的商业应用具有一定的实际意义。

1 基于BWDSP的FFT算法优化

1.1 基-2时间抽取FFT算法

快速傅里叶变换是离散傅里叶变换(Discrete Fourier Transform,DFT)的一种快速计算形式，可以很明显地减少计算量和运算时间。DFT正变换公式如式(1)所示:

(1)

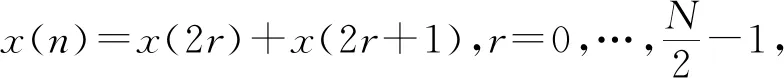
(2)

N点的FFT算法一共有m阶的蝶形运算，每一阶都有N/2形结构参与运算，每个蝶形运算(a+bj)(wr+jwi)需要一次复数乘法和两次复数加法，如图1所示，每一阶的蝶形运算共需要N/2次复数乘法和N次复数加法，所以一个N点的完整FFT运算需要(N/2)m=(N/2)lbN次复数乘法和NlbN次复数加法，时间复杂度为o(NlbN)。但是参与蝶形运算的数据需要从内存中读取两个输入数据和相应的旋转因子，然后将计算结果写入到寄存器中，读取和存放的数据量是一样的，并不能充分使用BWDSP硬件资源，运算时间也得不到减少。

图1 基-2时间抽取FFT蝶形运算单元

1.2 并行结构FFT优化

在按时间抽选的基-2 FFT算法中，每级任意两个蝶形运算都是互相独立的，在正确读取其旋转因子的情况下，蝶形运算单元顺序可以并行执行。为了充分利用BWDSP1042的SIMD和VLIW混合架构，减少FFT算法的运算时间，在时间抽选的基-2 FFT算法基础上进行结构调整，使用倒位序输入、自然序输出的FFT算法进行蝶形运算单元的并行处理，如图2所示。BWDSP中数据存储器划分为6个block，每个block大小为256 KB。把旋转因子与输入数据保存到不同的 block 块中，并且使用复数指令、位反序寻址指令、数据存储器读写指令等高效指令的特性来充分利用其带宽，有效减少旋转因子重复计算或访存，在充分发挥处理器优势的同时又能提高FFT算法性能。按时间抽选的基-2FFT实现的并行计算流程图如图3所示。

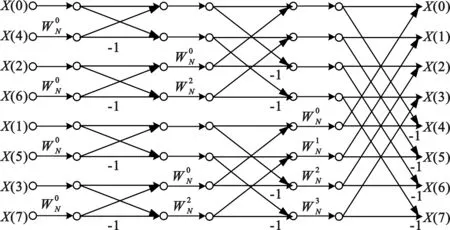
图2 倒位序输入、自然序输出8点FFT流图

图3 并行结构FFT流程图

1.2 1 024点的定点FFT算法优化实现

1.2.1 寻址方式选择

前四阶的蝶形运算合并时使用位反序寻址读操作、模八双字写操作的方式来优化。位反序寻址双字读访存指令来读取输入数据，读取指令为r7:6=br(N)[u0+=1,1]。

在以上这一条读取指令中，在寄存器r7:6前没有指定宏,则默认是使用4个执行宏{x,y,z,t}同时读数，一条指令能够读取8个定点数，利用4个执行宏同时读数可显著提高运行效率。位反序寻址指令是专门为FFT算法设计的，它能够将u0的基地址若干位前后颠倒，生成算法所需要的实际地址来进行后续的数据访存操作，但是，一旦修改过的基地址不参与反序操作，这种位反序方式能够保证数据访存的正确性，也提高了数据高效访存的效率。位反序的位数N是基于N点FFT算法的蝶形运算阶数lbN，当阶数是偶数阶时进行合并前四阶，当阶数是奇数阶时，前四阶合并结束后单独执行第五阶运算，其余均是采用两阶合并。

模八寻址方式将前四阶合并的计算结果按照顺序写入地址寄存器中，模八寻址指令为m[v0+=v10,v11]=xr41:40yr45:44zr43:42tr47:46。

数据的写入是根据运算宏通用寄存器堆中的数据按照宏{x,y,z,t}确定好的顺序存储到数据存储器中的，每条指令中4个宏中的通用寄存器堆的序号可以按照指令确定的数据各不相同。通过模八寻址写入的方式，能够改变不同宏之间不同的通用寄存器的值来改变前四阶合并结束后计算结果的顺序，从而保证输出的顺序是自然序。所以，本文在前四阶使用位反序寻址读操作、模八双字写操作，其他阶采用线性双字读写操作。只通过优化前四阶的寻址方式，是因为已经将倒位序输入的数据通过模八双字写入的操作将数据调整顺序，后面的蝶形运算将会按照模八寻址的写入数据顺序进行计算，所以前四阶寻址方式优化足以保证输出顺序是自然序，满足算法要求。

1.2.2 复数运算指令充分利用宏资源

BWDSP1042处理器提供了高效的16位定点复数同时做加/减以及除2操作指令，专门为定点数据运算设定的一种操作方式，大大减少了复数操作的指令周期。

{x,y,z,t}CHRm_Rn =(CHRm +/-CHRn),

{x,y,z,t}CHRm_Rn=(CHRm +/-CHRn)/2。

一个16位定点复数同另一个16位定点复数进行加/减运算，运算结果直接送到结果存储器，或者除2后送到结果寄存器。通过定点复数指令来实现定点的蝶形运算。xCHRm_Rn=(CHRm+/-CHRn)这条指令只能完成1个定点复数的加减运算，结果存入到xCHRm_Rn寄存器中，而指令CHRs=(CHRm +/- CHRn)能够计算4个定点复数，分别将结果存入到4个执行宏{x,y,z,t}CHRm_Rn中。对比可知，定点复数进行蝶形运算时，充分利用4个执行宏计算可显著提高运行效率。

2.2.3 多阶合并

传统算法中，计算完每一阶的结果将保存到寄存器中，在下一阶运算时通过处理器的寻址方式再将结果读取出来，在中间结果的写入和读取期间进行了大量的数据访存过程，占用了运行算法大量时间。所以，为了实现高效的访存，采用多阶合并的方式来提升运算效率，减少数据输入输出的操作。N点FFT共有lbN阶，每阶有N/2个蝶形运算，每个蝶形运算需要完成一次复数乘法，两次复数加法。由于1 024点FFT算法共有10阶运算，前四阶的旋转因子较为特殊，不占用乘法器资源，所以蝶形运算只是使用加法器即可。

假设点数N是大于等于64点的，在这里简单介绍一下多阶合并的思路:首先合并前四阶，然后根据N点FFT的阶数进行分支，若是偶数阶，直接跳转到两阶合并的模块；若是奇数阶，先计算第五阶的蝶形运算，再继续进行两阶合并模块。基于这个思路，1 024点定点FFT汇编实现就是将前四阶合并运算写入一次，第五、六阶合并写入一次，七、八阶合并写入一次，九、十阶合并写入一次，即前四阶合并，其余两阶合并后将结果写入内存。简单说明前四阶蝶形运算合并思路：

xr3=n||u2=u0+4||u4=u0+8||u6=u0+12

xr4=r3lshift -7

lc3=xr4

_cfft4:

读||定义旋转因子

读||定义旋转因子||计算

…

_cfftloop4:

读||写||计算

…

if lc3 b _cfftloop4

由于前四阶每次计算128个定点数，所以N点FFT算法所需要前四阶计算的循环次数是xr4=N/128。在_cfft4模块中，首先读取128个定点数,定义旋转因子，并进行合并第一次四阶蝶形运算。在_cfftloop4模块中继续读取输入，并行把在_cfft4模块中合并第一次四阶蝶形运算结果写入到存储器中，同时也并行读取的下一组128个定点数的蝶形运算。if lc3 b _cfftloop4基于零开销循环寄存器lc3的条件跳转指令，只要lc3不等于0，零开销循环寄存器lc3就自动减1，而且将跳转到_cfftloop4模块循环执行四阶合并；若lc3等于0，说明N点的四阶合并已经全部完成，就顺序向下执行，不再执行跳转。用零开销循环来判断N点的四阶合并是否全部已经完成，可以大大减少代码量，同时增加程序循环执行的效率。其余的两阶合并与前四阶合并的思路是一致的，利用多阶合并的方式比每一阶都将中间结果写入内存中节省了输入输出的访存时间。

1.2.4 指令并行、软件流水、循环展开

在FFT算法优化时，指令并行、软件流水、循环展开这三种优化方法一般都是交叉使用的，在这里把两阶合并后的结果与旋转因子合并运算的汇编程序来具体介绍这三种优化方法。

(1)指令并行

r5:4=[u0+=u10,u11]

r7:6=[u0+=u10,u11]r11:10=[w0+=w5,w6]

chr17=chr7*chr11

chr16=chr6*chr10

chr23=(chr5+chr17)/2

chr22=(chr4+chr16)/2

考虑到指令并行的原则，将程序优化为

r5:4=[u0+=u10,u11]||r11:10=[w0+=w5,w6]

r7:6=[u0+=u10,u11]

chr17=chr7*chr11||chr16=chr6*chr10

chr23=(chr5+chr17)/2||chr22=(chr4+chr16)/2

由此可见，原来占用7行指令行的程序现在值占用4行，一个蝶形运算就减少了3个实际运行周期。

(2)软件流水、循环展开

由编排规则可知，计算结果和读访存指令结果需要隔两行使用，等待写入寄存器的数据需要提前两行准备好，所以在这个规则下，仅仅进行指令并行远远不够，会存在许多气泡行使流水线出现卡拍问题。为了冲掉中间的气泡行使得流水线尽量不出现停顿，减少实际运行周期，程序基于软件流水、循环展开继续优化。

r5:4=[u0+=u10,u11]||r11:10=[w0+=w5,w6]

r7:6=[u0+=u10,u11]

r13:12=[u0+=u10,u11]||r9:8=[w0+=w5,w6]||

chr17=chr7*chr11||chr16=chr6*chr10

r15:14=[u0+=u10,u11]||chr23=(chr5+chr17)/2||chr22=(chr4+chr16)/2

r35:34=[u0+=u10,u11]||r3:2=[w0+=w5,w6]||chr19=chr15*chr9||chr18=chr14*chr8

r37:36=[u0+=u10,u11]||chr25=(chr13+chr19)/2||chr24=(chr12+chr18)/2

r5:4=[u0+=u10,u11]||r11:10=[w0+=w5,w6]||chr21=chr37*chr3||chr20=chr36*chr2

r7:6=[u0+=u10,u11]||chr27=(chr37+chr21)/2||chr26=(chr36+chr20)/2

_cfft1loop：

[v0+=v10,v11]=r23:22||r13:12=[u0+=u10,u11]||r9:8=[w0+=w5,w6]||chr17=chr7*chr11||chr16=chr6*chr10

[v0+=v10,v11]=r25:24||r15:14=[u0+=u10,u11] ||chr23=(chr5+chr17)/2||chr22=(chr4+chr16)/2

[v0+=v10,v11]=r27:26||r35:34=[u0+=u10,u11]||r3:2=[w0+=w5,w6]||chr19=chr15*chr9||chr18=chr14*chr8

r37:36=[u0+=u10,u11]||chr25=(chr13+chr19)/2||chr24=(chr12+chr18)/2

chr21=chr37*chr3||chr20=chr36*chr2

chr27=(chr37+chr21)/2||chr26=(chr36+chr20)/2

.code_align 16

If lc0 b _cfft1loop||r5:4=[u0+=u10,u11]||11:10=[w0+=w5,w6]

优化后代码的指令并行性大大提高，充分利用核内的4个执行宏，循环核心代码并行执行写入结果指令，读取下一循环所用数据指令和点乘、叠加运算指令，充分利用了硬件资源，大大提高了程序运行效率。

2 实验与分析

实验平台为BWDSP1042，Win10系统，Matlab版本为32位Matlab2012a，VS版本为VS2010，ECS版本为ECS 2.0。不同点数的输入数据来自于Matlab程序产生的数据文件以及相应的旋转因子文件。

2.1 实验结果及分析

汇编程序优化之前编写C语言程序，根据测试无误的C语言程序框架进行FFT汇编。本文重点介绍FFT基于BWDSP1042底层优化，C语言相关操作不再赘述。在BWDSP1042配套的集成开发环境ECS 2.0中完成汇编程序，使用Matlab产生数据以及生成误差图。

使用Matlab程序来验证FFT算法编写的正确性。将Matlab程序产生的输入数据和旋转因子加载到ECS中运行FFT汇编程序，将FFT汇编输出结果导出到一个指定的文本文件output.txt中，然后使用Matlab读取txt文件中存放的汇编输出数据，进行图形可视化，如图4所示。同时,Matlab调用自身FFT函数读取同样的输入数据，将计算结果进行可视化，如图5所示。

图4 FFT汇编结果图

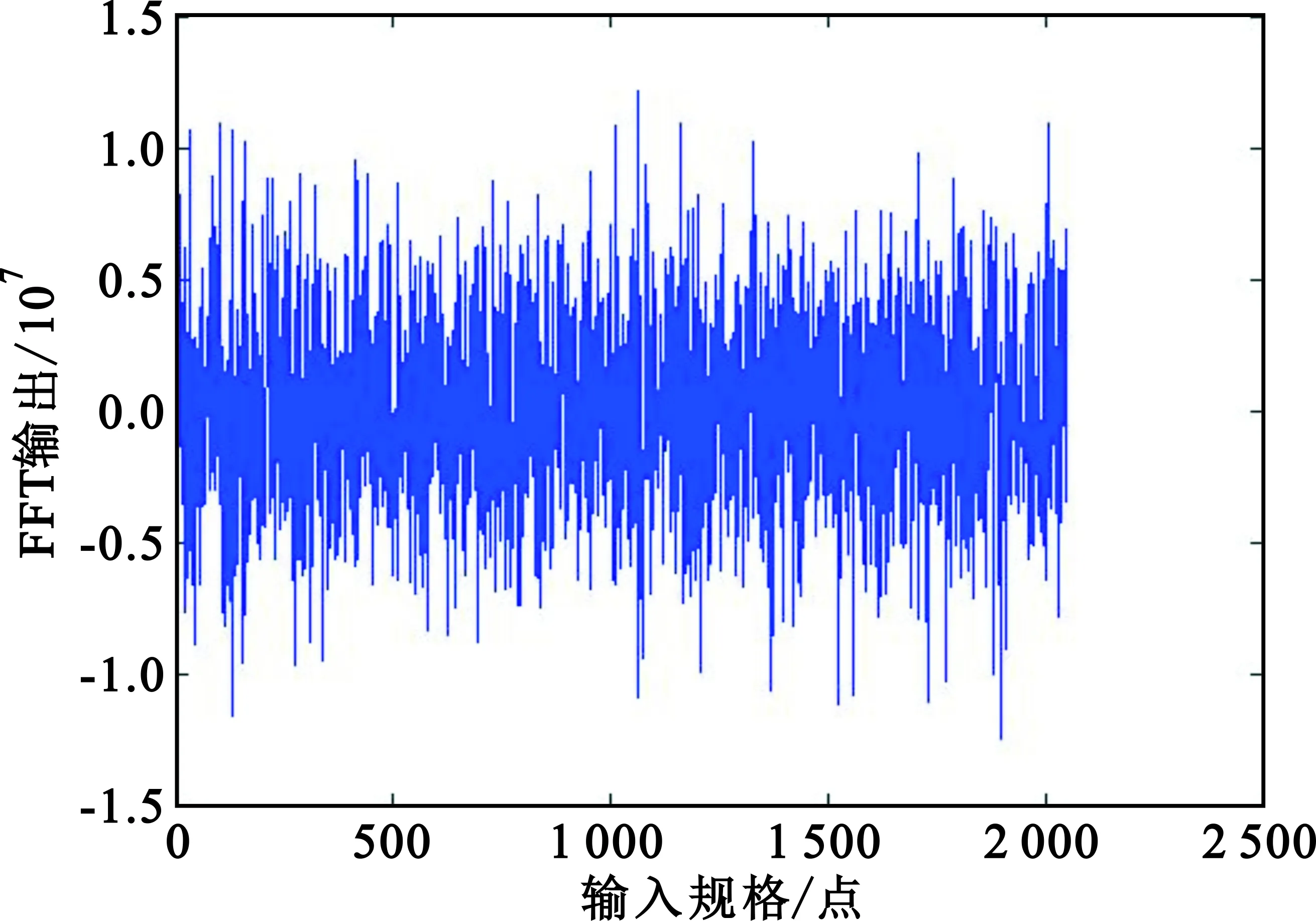
图5 Matlab结果图

由于Matlab中的函数库都已被广泛使用，其正确性毋庸置疑，所以将Matlab输出结果作为汇编优化函数的基本参照标准，将本文研究的算法与Matlab中FFT函数的输出结果进行对比，观察图4和图5，结果几乎一致，说明本文算法功能正确。为了进一步确定汇编算法的正确性，进行计算相对误差，如图6所示。

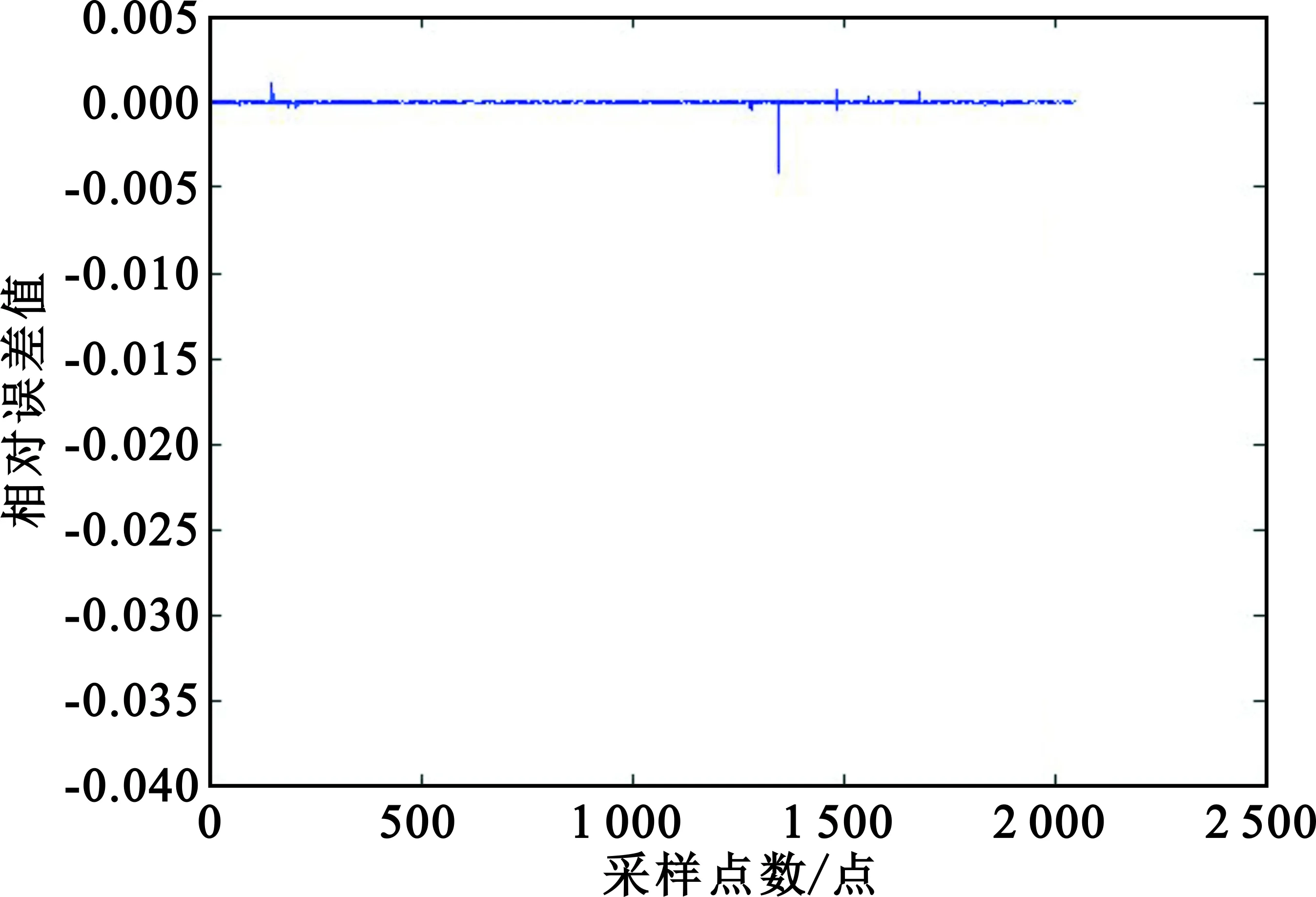
图6 相对误差图

观察图6可知，FFT汇编程序的输出结果与在Matlab中运行FFT函数的误差，大部分输入的计算结果基本一致，误差在0附近，在1 350点左右出现-0.004左右偏差。由于输入数据都是Matlab随机生成的浮点数，需要通过格式转换为定点数，实现定点数FFT汇编，在数据转换时也会出现些许误差，对输出误差也有相应影响。由图可知，输出误差在10-3级别，也在函数开发误差要求范围之内，说明基于BWDSP1042的FFT算法汇编正确。测试基于不同点数的FFT实际运行周期，并与BWDSP100、TMS320C6678函数对比，结果如表1所示。

表1 BWDSP1042实际周期比较

由周期指标可知，基于BWDSP1042的FFT算法实际运行周期应小于理论时钟周期的1.5倍。由表1可知，512点、1 024点、2 048点的FFT的实际运行周期分别为571拍、991拍、2 112拍，经计算该算法不同输入点数均满足函数库开发要求。本文将基于BWDSP1042的FFT算法与BWDSP100和TMS320C6678这两款高性能芯片应用函数库中的FFT算法的实际运行周期进行比较，运算效率均提升一倍以上，说明本文所研究的FFT算法在BWDSP1042的性能优化同时也体现了算法的实用性和优越性。

2.2 硬件资源成本

本文实现的N点的32位定点复数FFT共有lb(N)阶，每阶有N/2个蝶形运算，每个蝶形运算需要完成一次复数乘法、两次复数加法，所以完成一个蝶形运算需要4个加法器和4个乘法器。FFT函数主要是蝶形运算，从蝶形运算角度说明硬件资源消耗情况，如表2所示。

表2 硬件资源消耗说明

BWDSP1042中有4个增强的运算宏eC104+，每个宏中内部有8个加法器和8个乘法器，所以N/2个蝶形运算需要利用这些乘法器和加法器完成计算，大点数FFT运算对资源消耗的硬件成本更多。另外，FFT算法在实时性方面有一定要求，进而对BWDSP1042硬件性能具有较高要求，增加了硬件成本。

3 结束语

本文基于BWDSP1042的体系架构以及指令特点，改进了基-2时间抽取FFT算法结构，减少了FFT算法运算时间，优化了性能。定点格式的FFT算法由于进行了数据缩放，导致精度降低，虽然并不影响正确性，但应用于要求高精度的领域仍需继续提升精度指标。本文研究不仅对数字信号处理相关应用领域时频转换时间有一定的改善，而且对国产化芯片BWDSP1042的商业化应用以及走向工程应用具有实际意义。高性能FFT运算是芯片走向实际应用的重要一环，接下来的工作是在本研究基础之上，开发国产多核处理器BWDSP1042具有通用标准参数的高效率底层其他优化算法函数库，实现函数库与软件开发环境的集成，满足大多数用户使用，为DSP核心器件国产化打下基础，为该芯片成功推向民用市场奠定基础。