圆环相控阵天线瞬时带宽的分析与计算 *
2021-07-02梁宇宏邓宓原
梁宇宏 ,邓宓原,温 剑
(中国西南电子技术研究所,成都 610036)
0 引 言
相控阵天线具备波束指向和波束形状快速捷变的能力,并可在空间实现功率合成,在雷达、通信、导航等领域已经获得了广泛的应用[1-2]。近年来,随着系统需求的提高,对相控阵天线的瞬时带宽也提出了更高的要求,这就需要对相控阵天线的瞬时带宽进行分析和计算。
文献[3-4]对限制线阵相控阵天线瞬时带宽的影响因素进行了详细的分析与计算,这些影响因素包括频率变化引起的天线波束指向偏差和天线孔径渡越时间对瞬时带宽的限制,但现有文献集中在线阵相控阵天线或者平面阵的瞬时带宽的分析和计算,均未对诸如圆环相控阵天线在内的共形相控阵天线开展分析。
圆环相控阵天线是由均匀分布在一个圆周上的多个天线单元构成,作为一种常见的共形阵列天线,已经应用于通信、导航、识别等多个领域[5]。本文对限制圆环相控阵天线瞬时带宽的影响因素进行了详细的分析,给出了满足工程应用的计算方法,并比较了其与线阵相控阵天线的异同。
1 瞬时带宽的计算与分析
1.1 波束指向误差对信号瞬时带宽的限制
对于一个线阵相控阵天线,其中心频率为f0,若要求线阵相控阵的波束最大值指向为θB,则每个天线单元提供的相位补偿Δφ为
Δφ=2πf0(i-1)dsin(θB)/c 。
(1)
式中:i=1,2,…,M;d为阵元间距;c为真空中的光速。
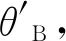
(2)
若使得两者相位补偿相等,即Δφ=Δφ′,则可以得到当频偏后的线阵相控阵天线的波束最大值指向为
(3)
同时也可以得到信号频率由f0变为(f0+Δf)后所引起的天线波束指向的偏移值为
Δθ=arcsin(f0sin(θB)/(f0+Δf))-θB。
(4)
如图1所示,建立一个排布在XOY面的圆环相控阵天线,相控阵天线半径为R,天线单元等角度排布在圆环上,令目标为P,分析圆环相控阵天线在XOY面上的扫描特性。
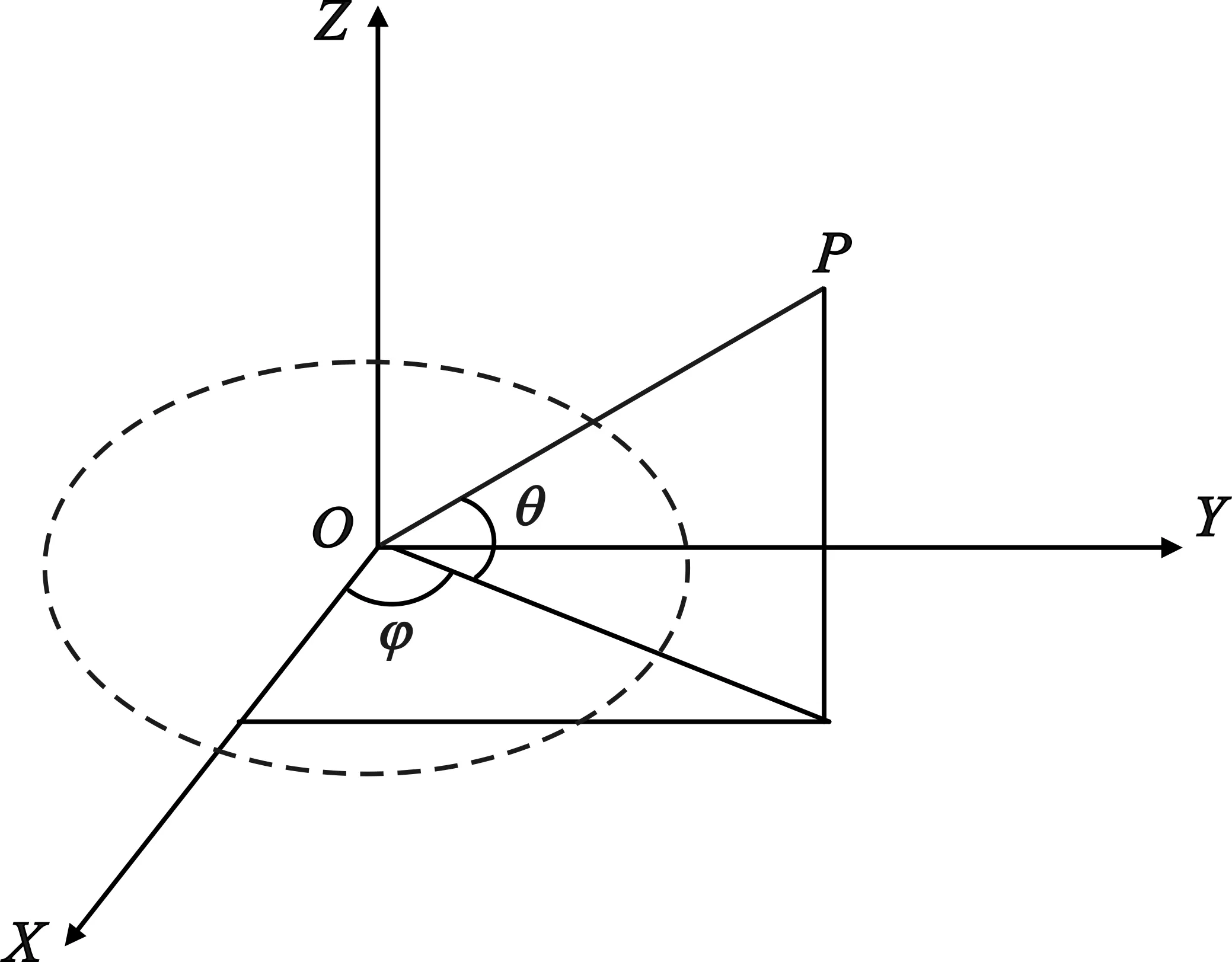
图1 圆环相控阵天线示意图
当相控阵天线波束的最大值指向(φ0,θ0)方向,则第i个天线单元提供的阵内相位差Δφ为
(5)
式中:xi和yi为第i个天线单元坐标。
令圆环相控阵天线实际辐射口面相对于+X轴对称,如图2所示。由于圆环相控阵天线在XOY面的扫描,则θ0=0,其法向波束指向为+X轴。
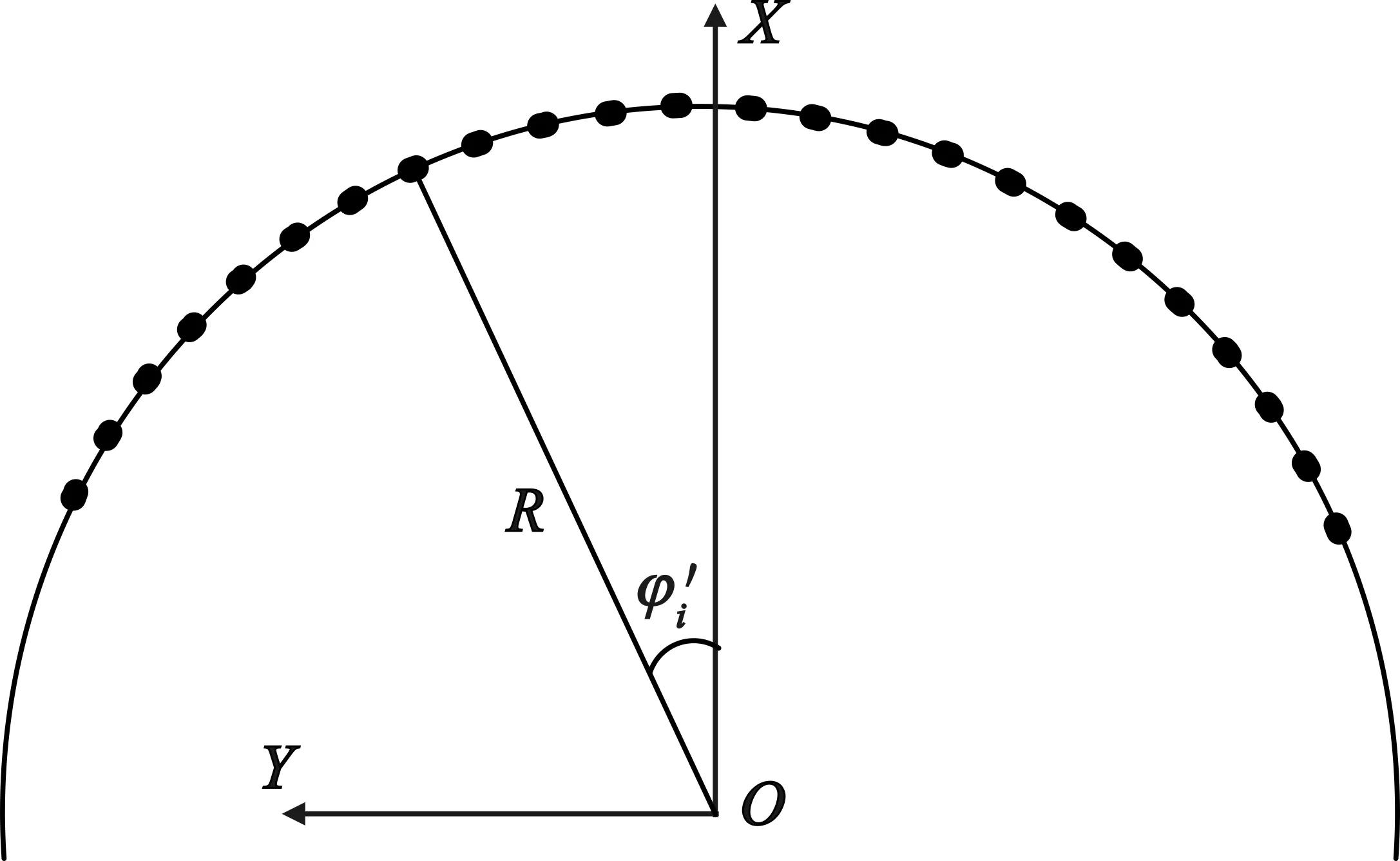
图2 圆环相控阵天线辐射口面示意图

(6)
(7)
设工作频率为相控阵天线的中心频率f0,若要求圆环相控阵的波束最大值指向为φ0,则每个天线单元的相位补偿Δφ为
(8)
当信号频率由f0变为(f0+Δf)后,此时圆环相控阵的波束最大值指向为φ1,则每个天线单元由移相器提供的相位补偿Δφ为
(9)
若使得两者相位补偿相等,即Δφ=Δφ′,令
x=cos(φ1) ,
(10)
(11)
则可以得到如下的一元二次方程:
(12)
求解该方程的根x,从而可以得到此时的波束最大值指向:
φ1=arccos(x) 。
(13)
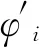
圆环相控阵各天线单元沿圆周等角度排布,其局部圆环相控阵天线示意图如图3所示。
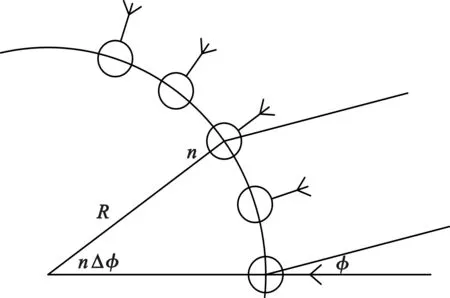
图3 局部圆环相控阵天线阵示意图
圆环相控阵各天线的和波束远场方向图为[6]
(14)
式中:R为圆阵半径;N为天线单元个数;EL为天线单元方向图;Vn为各天线单元的幅度加权值;φ为相邻天线单元间对应的圆弧角;f为工作频率;k为传播常数,k=2πf/c,c为真空中的光速。
当扫描至φ0时,圆环相控阵的和波束远场方向图为
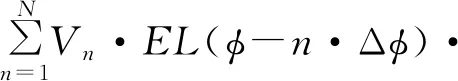
ejkR(cos(φ-n·Δφ)-cos(φ0-n·Δφ))。
(15)
由于天线的和波束宽度可能较宽,采用差波束指向来衡量实际波束指向更为精确,因此这里采用差波束指向来进行分析。对于如图2所示的单元个数N为偶数的圆环相控阵,关于+X轴对称的天线单元的相位差为π弧度。
此时,当扫描至φ0时,圆环相控阵的差波束远场方向图为
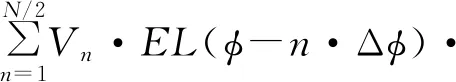
ejkR(cos(φ-n·Δφ)-cos(φ0-n·Δφ))+
ejkR(cos(φ-n·Δφ)-cos(φ0-n·Δφ))·ejπ。
(16)
举例说明,设圆环相控阵天线的中心频率f0,扫描角度为10°,频偏后的工作频率f1=f0+Δf,其中Δf=10%f0,此时可以得到工作频率f1时的波束指向为9.08°。图4所示为工作频率分别为f0和f1的差波束指向。
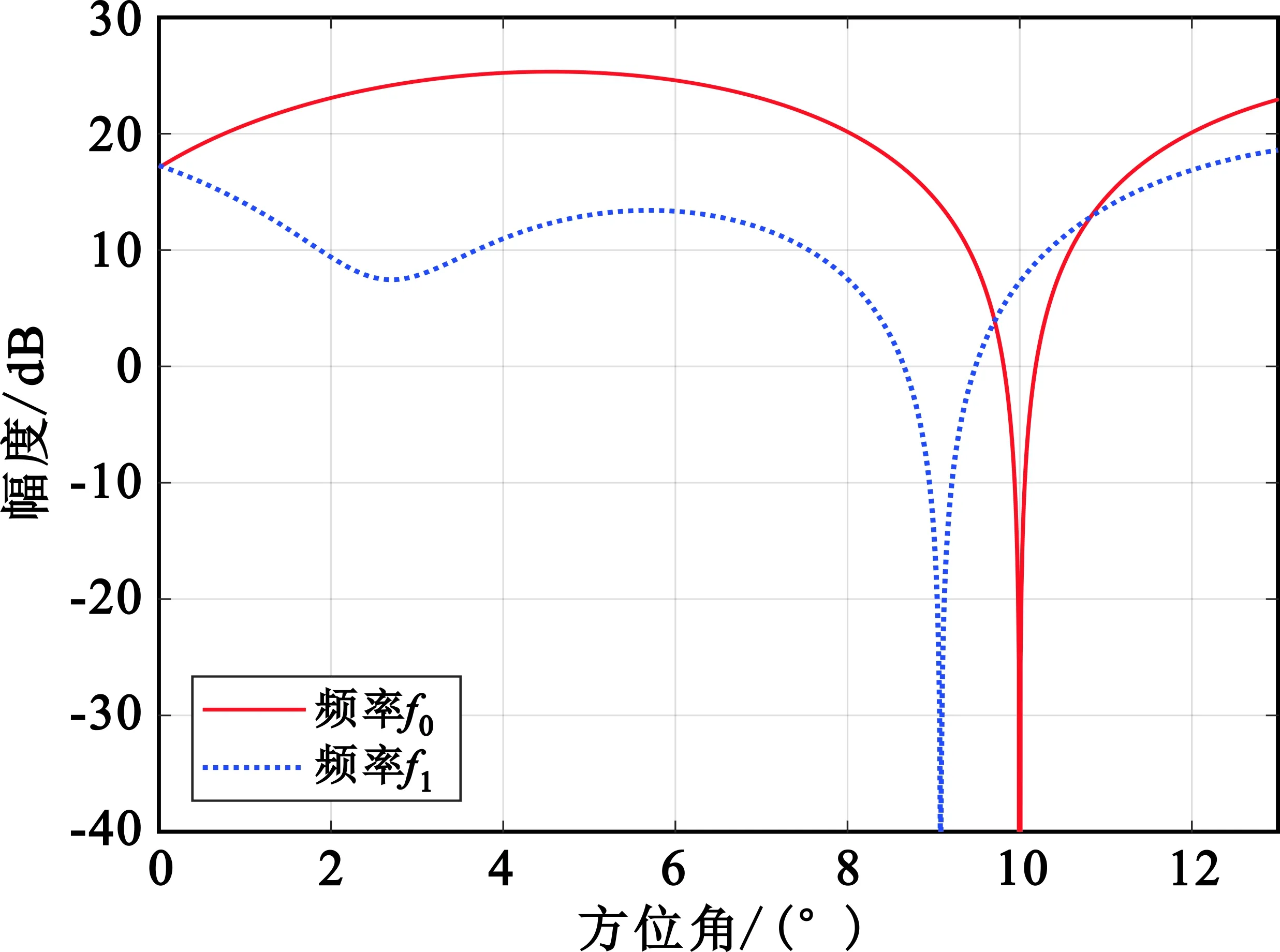
图4 工作频率分别为f0和f1的差波束指向
进一步地,可以根据最大扫描角度值得到圆环相控阵天线在扫描状态下频偏后的波束指向误差。可以发现在相同的扫描角度和频偏条件下,圆环相控阵天线与线阵相控阵天线的波束指向误差基本一致,两者的均方根误差小于0.01°。图5所示为圆环相控阵天线与线阵相控阵天线分别扫描10°和30°时,波束指向误差随频率变化的曲线图。

图5 波束指向误差随频率变化的曲线(扫描10°)

图6 波束指向误差随频率变化的曲线(扫描30°)
一般地,信号瞬时带宽应满足波束指向误差Δθ不超过半功率波束宽度1/4的准则,可根据具体使用场景来限定波束指向误差Δθ。通过以上分析,在满足要求波束指向误差时,可以得到允许的频率偏差Δf,此时允许的信号瞬时带宽为Δf1=2Δf。
1.2 孔径渡越时间对信号瞬时带宽的限制
相控阵天线所允许的最大瞬时信号带宽除受天线波束最大值指向误差的限制外,还受天线孔径渡越时间TA0的限制。
对于如图7所示线阵相控阵天线,假定相控阵天线的中心频率为f0,目标在θB方向上,阵列两端单元收到该同一目标信号的时间差为TA0,即第(N-1)号单元超前第0号单元TA0接收到从目标发出的信号。
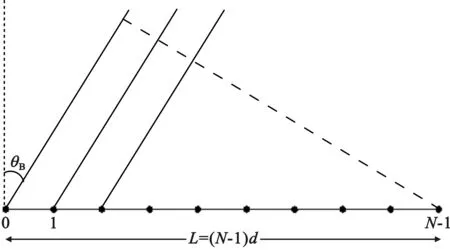
图7 线阵相控阵天线
由图7可知,到达天线线阵两端天线单元的时间差为[7]
TA0=Lsin(θB)/c 。
(17)
式中:c为真空中的光速。相控阵天线线阵两端两个单元之间的间距为
L=(N-1)d。
(18)

图8 圆环相控阵天线单元间的距离关系
圆环相控阵天线实际辐射口面的圆弧角通常不大于120°,即ψ0≤120°。
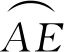

图9 TB随B点所在的角度φ变化的曲线(ψ0=90°)
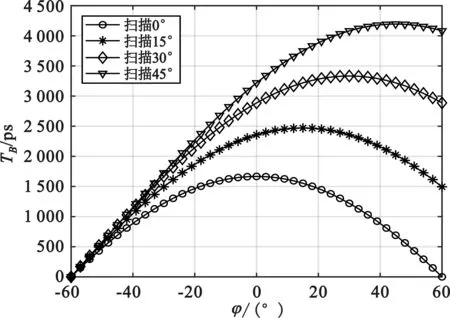
图10 TB随B点所在的角度φ变化的曲线(ψ0=120°)
由图9~10可知,圆环相控阵天线的孔径渡越时间与线阵相控阵天线有明显不同。对于特定的扫描角,线阵相控阵天线的孔径渡越时间随口径的增大而线性增大,并且其最大孔径渡越时间发生在线阵两端的两个天线单元;圆环相控阵天线的最大孔径渡越时间不一定发生在圆环两端的两个天线单元,而是与扫描角度有关,不能简单地用到达两端的两个天线单元的时间差来计算。显然,当扫描角度为0°时,圆环端点的天线单元与圆环中心的天线单元会产生最大孔径渡越时间。当扫描角度正向逐渐增大,圆环端点的天线单元与圆环中心右侧的天线单元会产生最大孔径渡越时间,并且该中心右侧单元逐渐右移;若扫描角度负向逐渐增大,则趋势相反。
令TBM=max(TB),信号瞬时带宽对TBM的限制至少应满足TBM≤1/Δf,通常,更严格的要求为TBM≤0.1/Δf。此时,可得Δf≤0.1/TBM。由此,由于孔径渡越时间对信号瞬时带宽的限制,此时圆环相控阵天线的信号瞬时带宽为Δf2=0.1/TBM。
当辐射口面圆弧角分别为ψ0=90°和ψ0=120°时,由于孔径渡越时间的限制,信号瞬时带宽随扫描角度的关系如图11所示。
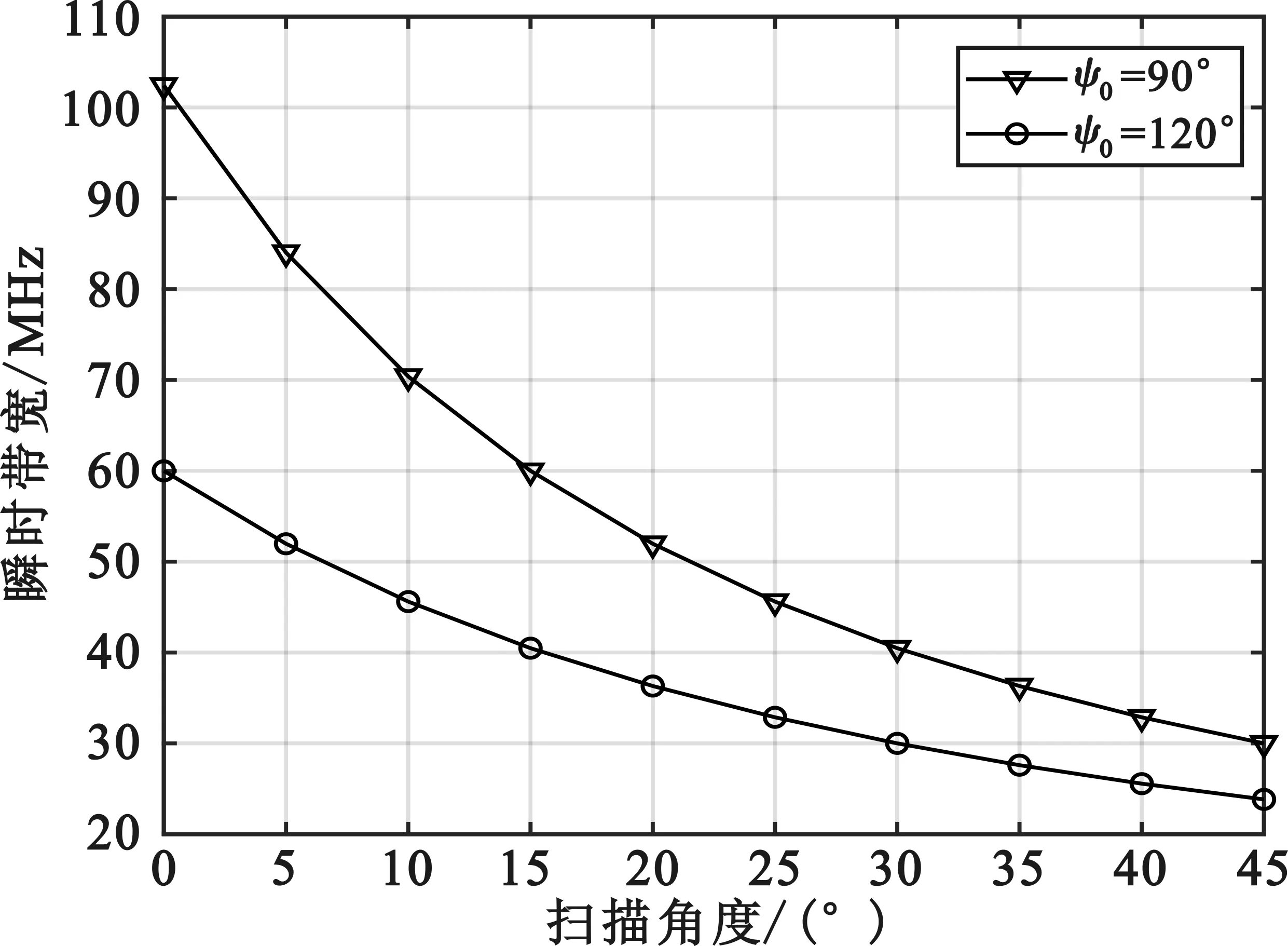
图11 信号瞬时带宽(ψ0=120°)
1.3 圆环相控阵天线的瞬时带宽
由前述可知,圆环相控阵天线的瞬时带宽受波束指向误差和孔径渡越时间的限制,此时,圆环相控阵天线的瞬时带宽为两者的最小值,即Δf=min(Δf1,Δf2)。
以一个中心频率为1 GHz的圆环相控阵为例进行计算说明。该圆环相控阵天线半径为1 m,40个天线单元沿圆周等角度排布,辐射口面圆弧角为ψ0=120°。相控阵天线需要在方位面±15°范围内扫描,要求瞬时带宽大于30 MHz,且在瞬时带宽内指向偏差小于等于1°。采用如上所述方法,可以计算在信号瞬时带宽内,波束指向偏差小于等于0.5°,满足系统对天线指向偏差的要求。若指向偏差为1°,则此时的信号瞬时带宽Δf1≥60 MHz;由于孔径渡越时间的限制,信号瞬时带宽可满足Δf1≥40.48 MHz。因此,圆环相控阵天线的瞬时带宽为两者的最小值,即Δf=min(Δf1,Δf2)=40.48 MHz。从计算分析看,该天线满足系统对于瞬时信号带宽的要求。
圆环相控阵天线的瞬时带宽与具体的扫描角度范围、允许的指向精度偏差等系统指标有关,如系统需要进一步拓展圆环相控阵天线的瞬时带宽,则可以采用射频延迟技术或者视频延迟技术。
2 结 论
相控阵天线的瞬时带宽受波束指向误差和孔径渡越时间的限制。基于此,本文对圆环相控阵天线的瞬时带宽进行了详细分析,给出了圆环相控阵天线瞬时带宽的计算方法,并比较了圆环相控阵天线与线阵相控阵天线瞬时带宽分析的异同。根据实际的应用需求,通过本文计算方法可以得到圆环相控阵天线的瞬时带宽,从而判断是否满足系统的需求,进而考虑是否需要采用射频延迟技术或者视频延迟技术以拓展圆环相控阵天线的瞬时带宽。本文的分析和计算方法对圆环相控阵天线的工程应用具有理论指导意义。
