椭圆钢丝旋转对弹簧切应力及刚度的影响

2021-07-02欧学昊周长城李雪

山东理工大学学报（自然科学版） 2021年6期

欧学昊，周长城，李雪

(山东理工大学交通与车辆工程学院，山东淄博 255049)

椭圆钢丝螺旋弹簧与圆钢丝螺旋弹簧相比，具有切应力分布更加均匀，更轻量化，并且节约安装空间等优点[1]。椭圆钢丝螺旋弹簧主要应用在高应力工况下，例如气门弹簧、离合器弹簧[2]，轨道车辆的一系悬挂弹簧组内簧也部分应用。

在椭圆钢丝弹簧的实际生产中，由于绕簧的精度和回火的影响，椭圆截面会产生绕截面形心旋转一定角度的变形[1]，该角度一般小于15°。通过有限元分析发现，弹簧在遭受同样载荷作用时，其所受最大切应力变大，在与高温冲击[3]、砾石冲击[4]等外界因素共同作用下，更容易出现弹簧断裂。

近年来，国内外学者对椭圆钢丝螺旋弹簧进行了研究。例如张英会[5]介绍了各式弹簧的应力和变形的简化近似计算公式；文献[6]对圆形钢丝弹簧与椭圆钢丝弹簧的应力分布进行比较分析；文献[7]对非圆形截面钢丝弹簧计算方法进行了探讨；文献[8]通过多次有限元分析对椭圆钢丝弹簧刚度、切应力进行分析，得到了最佳的截面参数；文献[9]通过有限差分法对椭圆钢丝的泊松方程进行求解，得到了椭圆钢丝弹簧应力分布的近似解；文献[10-11]均提出了水平椭圆钢丝弹簧切应力的计算方法。

文献[5-11]均未考虑工艺因素导致的椭圆钢丝截面的旋转。为了研究截面旋转角的影响、计算旋转椭圆钢丝螺旋弹簧切应力和刚度，本文基于弹性力学，推导旋转椭圆截面扭转切应力模型，通过分解的方法导出旋转椭圆截面弯曲切应力模型，采用叠加法得到弹簧的切应力分布模型；根据截面位移函数求得截面的极惯性矩，得到弹簧的刚度模型；利用WORKBENCH对弹簧截面切应力模型以及刚度模型进行仿真验证。

1 旋转椭圆截面轨迹方程

弹簧截面如图1所示。在xOy坐标系中，2a、2b分别为旋转椭圆截面的长轴与短轴；α为椭圆长轴与x轴的夹角，即截面旋转角，0≤α<π；θ为旋转椭圆截面边界上任一点A处的角度位置，0≤θ≤2π；F为弹簧所受载荷；D为弹簧的中径；令弹簧的有效圈数为n，弹簧的节距为t，弹簧的螺旋角为β，β=arctan(t/πD)。

如图1，椭圆在x1Oy1坐标系中的轨迹方程为

图1 旋转椭圆钢丝螺旋弹簧截面示意

(1)

椭圆在xOy坐标系中的轨迹方程即为旋转椭圆截面轨迹方程。由转轴公式[12]，两坐标系中的坐标关系为

(2)

将式(2)代入式(1)化简可得旋转椭圆截面轨迹方程为

px2+qy2-2(a2-b2)sinαcosα·xy=a2b2，

(3)

为方便下文描述，式中令

2 切应力计算模型

2.1 扭转切应力计算

扭转应力函数Φ应满足微分方程

∇2Φ=-2GK，

(4)

式中：G为切变模量；K为单位长度的扭转角。

根据侧面边界条件，扭转应力函数Φ在侧面即横截面的边界上等于零，即Φs=0，所以假设扭转应力函数Φ为

Φ=m·[px2+qy2-2xy(a2-b2)sinαcosα-a2b2]，

(5)

式中m为任意常数。

扭转应力函数Φ还应满足端面边界条件，即

M=2∬Φdxdy，

(6)

(7)

根据横截面上扭转切应力和扭转应力函数的关系，可得旋转椭圆截面上任一点的扭转切应力分量，用极坐标表示为

(8)

式中r1为旋转椭圆截面极径，且

式(8)是基于直杆推导的扭转切应力分量，如果应用到弹簧的螺旋线上，在曲率非常大时，会有较大的误差，所以需要扭转切应力分量乘以修正系数k对结果进行修正。修正系数k[7]为

所以受扭转的旋转椭圆截面任一点A的切应力示意如图2所示。

图2 受扭转的旋转椭圆截面切应力示意

2.2 弯曲切应力计算

截面还受剪力F作用产生弯曲切应力，如图3所示。将剪力F沿长轴方向和短轴方向分解，即等效于两个分力分别作用于水平椭圆截面，如图4所示。

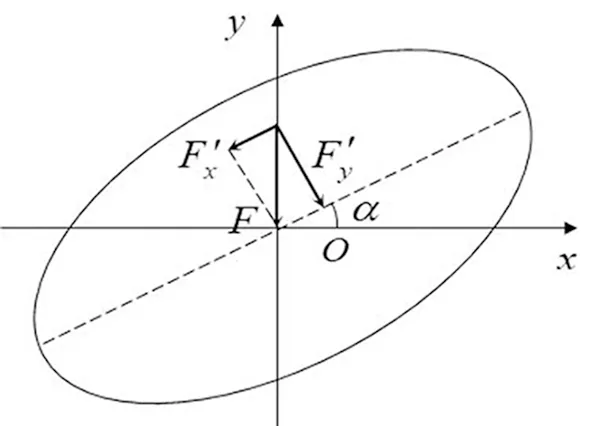
图3 剪力作用下的旋转椭圆截面

图4 等效受力的水平椭圆截面

首先考虑竖直剪力分量作用下的水平椭圆的弯曲切应力。令此状态下弯曲应力函数为Φw，Φw应满足微分方程：

(10)

弯曲应力函数Φw还应满足在横截面边界上为零的边界条件，即Φws=0，所以结合边界条件以及微分方程式(10)，假设弯曲应力函数Φw为

(11)

式中s为一常数。

将式(11)代入微分方程式(10)，可得

(12)

所以弯曲应力函数Φw为

(13)

如图4所示，令水平椭圆截面边界上任一点A的极径为r2，所在的角度位置为η，根据A点的角度位置关系，η=θ-α。

根据弯曲切应力分量与弯曲应力函数Φw关系，可以用极坐标表示竖直剪力分量作用下的水平椭圆任一点的弯曲切应力分量τ2zx1、τ2zy1为

(14)

同理，在水平剪力分量作用下水平椭圆任一点的弯曲切应力分量τ2zx2、τ2zy2为

(15)

水平椭圆截面任一点A在剪力F′的作用下的切应力分量等于两个剪力分量作用下切应力分量之和，即

(16)

将图4整体逆时针旋转α角，得到原旋转椭圆截面，任一点A的切应力分量的方向如图5所示，切应力分量大小不变，即

图5 剪力作用下的旋转椭圆截面切应力示意

(17)

2.3 复合切应力计算

如图6所示，将所求旋转椭圆截面上任一点A的扭转切应力分量与弯曲切应力分量叠加，得到旋转椭圆截面上任一点A的复合切应力分量

图6 切应力分量之间角度关系

(18)

则旋转椭圆截面任一点A的复合切应力τ为

(19)

2.4 WORKBENCH实例仿真验证

椭圆钢丝螺旋弹簧中径D=320 mm，螺距t=60 mm，有效圈数为n=6，截面长轴2a=40 mm，短轴2b=30 mm，材料切变模量G=76.923 GPa，弹簧受轴向载荷F=3 000 N。

为了验证切应力计算的准确性，根据弹簧参数建立α = 0°、15°、45°和165°的椭圆钢丝弹簧模型，分别导入WORKBENCH中，以α=0°的椭圆钢丝螺旋弹簧有限元模型为例，如图7所示。

人文主义精神是一种普遍的人类自我关怀，表现为对人的尊严、价值、命运的维护、追求和关切[4]。受市场经济等因素影响，我国医疗卫生事业中部分医务人员道德素质下降，医患关系日益紧张，对医学生自身发展和病人健康造成冲击，医学的人性光芒日趋黯淡，医学的人文主义精神衰落，同样也对整个社会的伦理道德产生严重冲击。为此，加强医学生人文主义教育成为高等医学院校思想政治教育的主要任务，具体内容及实施路径见图1。

为了使弹簧受力均匀，在弹簧上端与下端各加一弹簧座。设置材料参数：切变模量为76.923 GPa；为方便划分更佳网格，对弹簧部分进行了适当切割；对弹簧有效圈部分使用Multizone网格划分方法，划分5 mm单元格；对上端弹簧座施加轴向位移约束，下端弹簧座施加固定约束，在上端弹簧座的中心位置施加竖直向下的载荷，F=3000 N。对模型的有效圈部分切应力进行仿真，得到不同α角的椭圆截面的切应力云图，如图8所示。

在切应力仿真结果中，基于α = 0°、15°、45°、和165°的椭圆钢丝弹簧截面应力云图，获取截面边界的切应力数据，可以得到计算曲线与仿真数据，如图9所示。

由图9可知，α=0°、15°、45°和165°的椭圆截面的应力分布计算曲线与仿真数值变化规律几乎一致；根据得到的各α角的椭圆截面切应力的计算值与仿真值，其切应力最大相对偏差分别为1.78%、1.66%、1.79%、1.63%。

将α=0°、15°、45°和165°的椭圆截面的切应力分布数据通过4次Fourier拟合，与计算值进行对比，见表1，各α角的椭圆截面最大切应力τmax的相对偏差均小于1%，最大切应力所在角度θ的相对偏差均小于1%，因此，旋转椭圆钢丝螺旋弹簧切应力计算模型是正确的。

表1 最大切应力及其角度位置分析

由表1可知，由于工艺精度等原因，若截面旋转角达到15°，实际椭圆钢丝弹簧的最大切应力会较水平椭圆钢丝弹簧增大8.96%，并且最大切应力位置也会有所变化，所以提高工艺水平是非常重要的。

3 刚度计算模型

3.1 刚度计算

将式(8)用直角坐标表示为

(20)

令截面扭转位移函数为φ，横截面上的扭转切应力分量与扭转位移函数φ关系为

(21)

联立式(20)与式(21)，两方程分别对x，y积分，可得

(22)

扭转位移函数φ若要满足式(22)，则一定满足:

所以扭转位移函数φ为

(23)

极惯性矩Ip的计算方法[13]为

(24)

将式(23)代入式(24)，化简得到截面旋转角α的椭圆极惯性矩为

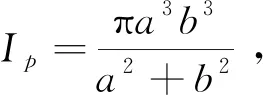
(25)

所以旋转椭圆钢丝螺旋弹簧的刚度R为

(26)

由式(26)可知，表达式中没有α，说明旋转椭圆钢丝弹簧的刚度R与截面旋转角α无关。

3.2 WORKBENCH仿真验证

基于式(26)，根据旋转椭圆钢丝弹簧参数，可以得到弹簧的计算刚度值为67.608N/mm；对α=0°、15°、45°、165°的旋转椭圆钢丝螺旋弹簧模型整体变形进行仿真求解，得到各截面旋转角α的椭圆钢丝弹簧的最大变形量λmax，用载荷F除以各最大变形量λmax，可以得到各截面旋转角α的椭圆钢丝螺旋弹簧刚度，见表2。

由表2可知，旋转椭圆钢丝弹簧的计算刚度值与仿真值的相对偏差均小于1%，证明了刚度计算的正确性，旋转椭圆钢丝螺旋弹簧的刚度R与截面旋转角α无关，所以实际生产中的椭圆钢丝螺旋弹簧的截面旋转角仅影响切应力大小及分布，对弹簧的刚度无影响。