一种六自由度手术机器人的运动学计算和仿真

王庆升， 周惠兴,2， 王衍学

(1.北京建筑大学 机电与车辆工程学院， 北京 100044; 2.北京建筑大学 建筑机器人与智能设备智能实验室， 北京 100044)

微创外科手术机器人是集众多前沿科技于一体的综合体，在微创外科领域是革命性的手术工具。手术机器人技术是当前医疗机器人领域的研究热点，受到国内外机构的高度关注[1]。与传统手术方式相比，微创手术技术大幅提高了外科手术的操作精度，微创手术创伤面积小，进一步减少了术中出血量和术后不良反应的发生，加快了术后的恢复速度。现代医疗机器人技术发展迅速，已在世界各地医院中得到广泛应用，微创外科机器人技术还在不断向前发展，具有广阔的市场前景。

将手术机器人应用到微创外科手术中，必须严格保证机器人在身体介入点处不会对人体造成额外伤害，因此需要机器人提供一个空间位置不变的固定点，即远程运动中心(Remote Center-of-Motion, RCM)，简称为远心点，其概念由Taylor教授提出[2]。

手术机器人约束RCM的方式主要有2种，一是通过特殊设计的机构约束实现，二是通过算法控制多关节联动实现[3]。机构约束方式因为控制简单、机构安全等特点，在手术机器人中应用较为广泛。目前手术机器人中的RCM机构主要有平行四边形机构、球面关节机构、圆弧导轨机构等[4]。美国直觉外科公司的da Vinci手术机器人系统[5]，采用的是双平行四边形的机构约束方式，哈尔滨工业大学“华鹊”、上海交通大学“神刀华佗”机器人均采用的是双平行四边形机构[6]。平行四边形约束由于冗余自由度过多[7]、体积庞大，导致机械臂之间易发生干涉[8]。

多关节联动方式的机器人本身不具有RCM机构，手术过程中的RCM通过算法控制的关节联动实现。多关节联动方式可以降低对机构的依赖，通用性更高，但对算法稳定性和可靠性的要求较高，机器人整体的控制难度较高。德国宇航中心的DLR MIRO机器人采用的是多关节联动方式[9]，该机器人外部的7个关节均为主动驱动关节，机器人系统通过自由度的冗余实现手术切口处的定点运动。但是该机器人自由度冗余，需要算法解决冗余自由度，且容易发生奇异。

1 研究分析

手术机器人模型设计的关键在于RCM机构设计，一个合理的RCM机构可以以最少的机构数量满足自由度要求。通过研究分析国内外多种手术机器人的机构设计，本文提出了一种采用多关节联动方案的串联六自由度的手术机器人模型，6个关节均为主动驱动关节，模型具有结构紧凑、体积小巧、无额外自由度冗余、不易发生自身干涉等特点。此模型为多关节联动方案提供了一个思路和方法。

2 建模与计算

2.1 D-H法建模

本文的模型创建采用标准D-H法(Standard Denavit-Hartenber)，用齐次变换矩阵来描述连杆间的位姿变换，从而建立运动学方程(图1)。

图1 手术机器人模型Fig.1 Surgical robot model

模型包含5个旋转关节和1个移动关节，确定机器人模型的D-H参数见表1。为了方便后期扩展关节数量，关节参数编号从4开始计。

表1 D-H参数

θi为关节旋转变量，di为平移关节的移动变量，ai为连杆间坐标系变换的距离偏置常量，αi为连杆间坐标系变换的偏置角常量。忽略末端执行器夹手开合动作的额外自由度，按照D-H法建立的六自由度机器人各部件坐标系如图2所示。

图2 机器人D-H模型Fig.2 Robot D-H model

2.2 正运动学

采用D-H法得到连杆间的齐次变换矩阵，将变换矩阵连续右乘得到模型的正解方程。正运动学是运动学逆解的基础，将逆解代入正运动学可以验证逆解的正确性。

由标准D-H变换法，相邻2个连杆i对i-1之间的齐次变换矩阵i-lTi为：

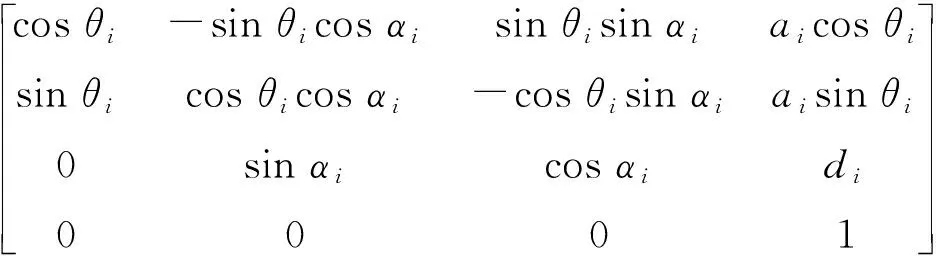
(1)

式中：Rotx、Rotz分别表示绕x、z轴的旋转，Transx、Transz表示沿x、z轴的平移，变量和常量由表1确定。

根据式(1)可以分别计算出每2个连杆之间的变换，连续右乘得到从基座到末端的位姿变换，模型末端位姿矩阵Tend为：

(2)

式中：nx、ny、nz分别表示末端坐标系的x轴在基坐标系x、y、z轴的方向余弦，ox、oy、oz分别表示末端坐标系的y轴在基坐标系x、y、z轴的方向余弦，ax、ay、az分别表示末端坐标系的z轴在基坐标系x、y、z轴的方向余弦，px、py、pz表示末端坐标系原点在基坐标系的位置坐标。

2.3 逆运动学

机器人的逆运动学是求解机器人的关键问题，是运动规划和运动控制的基础。运动学逆解是给定末端位置和姿态，求出各关节变量。

求运动学逆解的常见方法有解析法和数值法，解析法又可以分为几何解法与代数解法，本文基于矩阵逆变换的方法，即Paul等提出的反变换方法求解关节变量，采用解析法中的分离变量法进行数值计算[10]。

机器人前3轴的3个坐标系原点重合，形式上与zyz欧拉角相同。后3轴分别为移动、旋转、旋转关节。该模型3个相邻轴相交于一点，满足Pieper准则，存在封闭解。

机器人位姿变换矩阵如式(2)所示，对式(2)矩阵逆乘反变换，联立等式各项参数可得：

-s4s6+c4c5c6=-axs8+c8(nxc9-oxs9)

(3)

c4s6+s4c5c6=-ays8+c8(nyc9-oys9)

(4)

s5c6=-azs8+c8(nzc9-ozs9)

(5)

-c4s5=axc8+s8(nxc9-oxs9)

(6)

-s4s5=ayc8+s8(nyc9-oys9)

(7)

c5=azc8+s8(nzc9-ozs9)

(8)

s4c6+c4c5s6=-oxc9-nxs9

(9)

-c4c6+s4c5s6=-oyc9-nys9

(10)

s5s6=-ozc9-nzs9

(11)

-d7c4s5=px-a9nx-a8(nxc9-oxs9)

(12)

-d7s4s5=py-a9ny-a8(nyc9-oys9)

(13)

d7c5=pz-a9nz-a8(nzc9-ozs9)

(14)

式中：si表示sinθi，ci表示cosθi。本文机器人关节角中θi的取值为(-π,π]。

2.3.1 求解θ9

将式(6)～(8)分别带入式(12)～(14)得：

(15)

令：

(16)

式中：Px、Py、Pz是公式化简的临时变量。

等式组(15)消去变量d7，得：

(17)

当Pz-a8(nzc9-ozs9)=0时，等式组(17)仍成立，但对于求解θ8、θ9没有意义。

(18)

将式(18)代入式(17)并化简，可分离变量θ8：

(19)

将式(19)交叉相乘化简可得式(20)：

0=(Pz-Rza8)(PxRyaz-PxRzay+PyRzax+…
-PyRxaz+PzRxay-PzRyax)

(20)

令：

(21)

将式(18)代入式(20)可得只含θ9的方程：

(22)

由式(14)可知，当且仅当d7c5=0时，表达式Pz-a8(nzc9-ozs9)的值为零，否则此项不为零。由式(15)可知，此项为零对求解θ9无意义。

由式(22)可得：

(23)

式中：(1±1)π/2为0或π，θ9可求得2个值。若Pm=Pn=0，将式(2)中的各个参数nx、ox、ax、px、ny、oy、ay、py、nz、oz、az、pz的表达式代入可得a8+d7s8=0，此时位置奇异，θ9无唯一解。本文所述唯一解是指在反三角函数指定值域内唯一，而不是只有一个解，实际上在(-π,π]内可能有2组解。

2.3.2 求解θ8

令：

(24)

由式(19)、(24)可得：

(25)

此处θ8将会求得4个值。式(24)中Pxz=Rxz=Pyz=Ryz=0，将式(2)中的各个参数nx、ox、ax、px、ny、oy、ay、py、nz、oz、az、pz的表达式代入式(24)可得：

(26)

即d7=0或c4c6=s4s6c5=0，此时位置奇异，θ8无唯一解。因参数设定d7>0，只考虑c4c6=s4s6c5=0，此状态可具体分为4种情况：c4=s6=0、c4=c5=0、c6=s4=0或c6=c5=0。此4种状态虚拟六轴的4、5、6轴将会形成万向节锁。

2.3.3 求解d7

由式(15)可得：

(27)

w可取x、y或z。此处d7将会求得4个值。由式(6)～(8)可知，式(27)中分母分别为-c4s5,-s4s5,c5,显然不会全部为零，故d7有唯一解。

2.3.4 求解θ5

由式(7)可得：

θ5=±arccos[azc8+s8(nzc9-ozs9)]

(28)

此处θ5将会求得8个值，由向量内积可知|azc8+s8(nzc9-ozs9)|≤1。

2.3.5 求解θ4θ6

观察式(5)～(7)、(11)可知，θ5的取值将影响θ4、θ6的求解。

1)当s5=0时，即θ5为0或π，此时θ4、θ6没有唯一解，只有θ4+θ6的公共解。此状态下，由式(9)～(10)可得：

(29)

式中：s46表示sin(θ4+θ6)，c46表示cos(θ4+θ6)。

由式(29)可得：

θ4+θ6=atan2(-oxc9-nxs9,oyc9+nys9)

(30)

若-oxc9-nxs9=oyc9+nys9=0，代入ox、oy、nx、ny得：

(31)

显然等式组不成立，故θ4+θ6有唯一解。

2)当s5≠0时，由等式(6) (7)、(5) (11)可得：

(32)

(33)

此处θ4、θ6将分别求得4个值。若ayc8+s8Ry=axc8+s8Rx=-azs8+c8Rz=-ozc9-nzs9=0，代入nx、ox、ax、ny、oy、ay、nz、oz、az表达式得：

(34)

显然，等式组不成立，故假设不成立，θ4、θ6有唯一解。

2.4 逆解验证

将上述算法脚本编程，设定机器人的关节连杆偏置参数值a8=a9=50 mm，d7取值为(0,1 000]，设定θ4、θ5、θ6、θ8、θ9取值均为(-π,π]。使用rand()随机函数生成位姿T=(-3.05,-2.72,1.37,233.25,-90.86,-19.82)，求得8组逆解，见表2。

表2 随机位姿的8组逆解

3 基于ROS的仿真

ROS(Robot Operating System)机器人操作系统，采用分布式处理，提供硬件抽象、设备控制等标准的操作系统服务，支持对Linux硬实时扩展[11]，集成RViz、Gazebo、rqt等强大的工具包，兼容多种编程语言，可实现跨平台跨语言的源代码共享。

基于ROS对机器人进行运动仿真，首先在三维建模软件中创建机器人的模型。3个坐标系重合的结构只在理论上存在，实际上物理结构件都会存在尺寸，如此复杂的结构模型很难直接做成足够紧凑的机械结构，所以本文仿真时额外设计3个自由度，目的是在RCM处提供4、5、6轴所提供的3个姿态。由于额外3个自由度的存在，原本重合的4、5、6坐标系可以分开，形成更方便求解的通用模型。

模型建立完毕后使用插件生成指定的URDF文件，使用运动控制工具MoveIt!配置参数生成功能包，使用Python接口编写逆运动学控制程序，利用OMPL/SBL进行运动规划，并使用可视化工具RViz进行可视化验证，展示了RCM运动仿真和圆弧插补运动仿真。

3.1 URDF模型文件

统一机器人描述格式(Unified Robot Description Format，URDF)是ROS用来描述机器人模型的一种xml语言，文件包含模型的形状、大小、惯量、质心、颜色等基本属性，还包含机器人的动力学参数。采用URDF格式来描述机器人模型，对于复杂的模型可使用sw2urdf插件将Solidworks模型转换为URDF文件(图3)，在模型中设置完整的坐标系和转动移动轴，该插件可以辅助生成并导出对应的URDF文件和ROS功能包。

3.2 运动仿真

Moveit!是ROS中用于运动规划和运动控制的强大的工具集，包括用于运动规划的运动学分析、运动学算法、动力学、运动规划、路径规划、轨迹规划等。MoveIt!是实现运动仿真功能的一个主程序，它集成于ROS通讯框架，并兼容ROS的工具，如可视化RViz、物理仿真Gazebo、机器人描述文件URDF等。本文使用Moveit Setup Assistant来辅助创建整套的功能包，MoveIt!核心组件move_group提供3种用户自定义算法接口，分别为C++接口、Python接口、GUI接口，为了方便测试和调试算法，选择Python接口，使用其moveit_commander功能包API、KDLKinematicPlugin运动规划库。使用MoveIt!进行关节空间点到点运动仿真，绕固定点运动的运动轨迹如图4所示。

图3 使用sw2urdf Setup创建URDF文件Fig.3 Using sw2urdf Setup to create a URDF file

图4 机器人运动仿真Fig.4 Robot motion simulation

点对点往复运动时，使用rqt_plot获取关节角度变化曲线，如图5所示。关节位置/joint_states/position[0-8]纵坐标分别表示1～9关节弧度位置。

为了更好地检验算法和测试机器人的性能，研究编写了一个简单的圆弧插补程序，可使机器人在绕定点运动的同时，执行器末端画圆，轨迹仿真如图6所示。

图5 各关节角度变化曲线Fig.5 Angle change curve of each joint

图6 圆弧插补运动仿真Fig.6 Circular interpolation motion simulation

4 结论

本文提出一种串联六自由度手术机器人模型，推导了机器人模型在基座固定的情况下，绕工作空间内任意位置RCM运动的算法。运用D-H法分别进行了运动学建模和运动学分析，基于矩阵求解的思路求得了逆解，并通过编程验证了逆解的正确性。通过对方程变量的分析，列举了发生奇异的位置和末端位姿参数的有效取值范围。提出了一种基于ROS的机器人运动控制及仿真的快速实现方法，充分利用了三维软件生成的模型，结合MoveIt!和RViz工具，较为便捷地模拟了自定义算法的机器人控制，形象地展示了机器人仿真运动的过程。此运动学计算和仿真可为此机器人后续研发提供计算研究基础。