浅谈二次函数在高中数学中的重要作用

黄 亮

（江苏省南京市聋人学校 江苏南京 210007）

一、深入了解二次函数的概念与基础

在初中数学教育中对函数有了介绍与理解，而踏入高中数学以后会在此基础上再次巩固，加深对函数概念、基础知识的理解，并基于映射观点来研究函数的基本概念与原理，让学生对函数概念有一个更全面的理解。

二次函数的概念为：二次函数是从一个集合A(定义域)到集合B(值域)上的映射f：A→B，使得集合B中的元素y=ax2+bx+c(a≠0)与集合A的元素x对应，记为y=ax+bx+c(a≠0)。

这里ax2+bx+c表示对应法则，又表示定义域中的元素x在值域中的象，借助集合与映射让学生对函数概念有更细致的理解，等到学生掌握基础函数概念与理论，就可以进一步展开下面问题的指导教学。

典型案例1：已知y=5x+2x+7，求 f(x+1)在解答该类型题目时，应当把 f(x+1)理解为自变量做x+1的函数值，而非x=x+1时的函数值。

典型案例2： f(x+1)=3x2+x+5，求 f(x)这种类型题目的本质是求对应法则，即要求在已知的对应法则 f 下，当定义域中元素x+1的象为3x2+x+5时，求定义域中元素x的象。该类型题目有两种求解方法：

方法1：采用适应性比较强的变量代换方式

令t=x+1，则x=t-1，因为 f (t+1)=3(t-1)2+(t-1)+5=3t2-5t+7，从而得出 f(x)=3x2-5x+7。

方法2：把题目所给的表达式表示成x+1的多项式

f(x+1)=3x2+x+5=3(x+1)2-5(x+1)+7，

再用x代x+1得出 f(x)=3x2-5x+7。

二次函数类知识涵盖比较广，除了以上内容，还考察二次函数单调性知识，比如让学生熟练掌握二次函数y=ax2+bx+c在区间(-∞，-b/2a) 及[-b/2a，+∞]上的单调性相关结论，并做系统证明，而单调性学习也需要结合图形共同理解，加深学生对函数知识的掌握。

典型案例3：画出下列函数的图像，并通过图像来研究其单调性。

(1)y=x2+4|x+1|+6

(2)y=3|x2+2|

(3)y=x2-2|x|+2

对于这类比较典型的题型，学生应该关注二次函数与这些函数直接的联系与差异，学会将含有绝对值记号的函数用分段函数去表示，并在此基础上画出图像。

经典案例4： f(x)=2x2-4x-2，其在区间[t，t+1]上的最小值为a( t )。求：a( t )，并画出y=a( t )的图像。对于这类题型的在解答时，学生首先应该认真审题，理解问题求解内容，然后思路清晰分析问题。一个二次函数在实数集合R上要么只有最大值要么只有最小值，但是当定义域产生变化的时候，取最小值或者最大值的情况也会随之发生变化。解答思路如下：

解： f (x)=2x2-4x-2=2(x-1)2-4，在x=1时，取最小值-4

当1∈[t，t+1]，即0≤t≤1，a( t )=-4

当t＞1时，a(t)= f ( t )=2t2-4t-2

当t＜0时，a(t)= f ( t+1)=2t2-4

二、二次函数在高中数学中的重要作用

二次函数为初中函数的进一步学习内容，也为基本的幂函数，函数内涵丰富，且拓展考查知识点多。通过二次函数学习，学生需要掌握函数概念、图像、奇偶性单调性，尤其是函数知识需要建立起不等式、方程、以及函数之间的紧密联系，因此这也是二次函数比较困难的点，需要学生深入学习。所以对二次函数的理解应该从数学思想、知识、方法以及应用上入手，进而充分锻炼学生数学思维，以更好地适应二次函数的演变题型，灵活思考。

进一步研究二次函数发展，这个章节知识是常考对象，甚至与各个章节知识有着紧密联系，如解析几何以及导数等高中主体知识与二次函数的有机结合，3个二次的等价运用等，考察的重点则分布在不等式的范围、函数的零点、方程根的分布、等价转化相关函数最值、二次函数的图像与性质等内容上。下面结合常见的高考二次函数相关题型，再做相关重要性介绍：

经典数形结合题型研究

如图，抛物线y=ax2+bx+c(a≠0)过点(1，0)和(0，-2)，且顶点在第三象限，设P=a-b+c，则P的取值范围是( ）

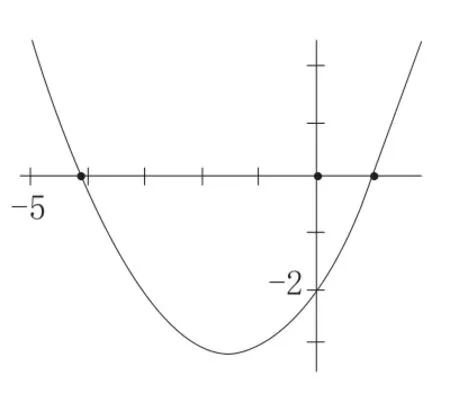
A.-4

B.-4

C.-2

D.-1

将两个点坐标代入函数解析式，从而得到a+b+c=0和c=-2这两个结论，更进一步的结果是a+b=2，然后就由顶点在第三象限想到顶点坐标均为负数，想到列两个不等式，然后……就没有然后了，全开始卡壳。本题是一道选择题，所以解析法用在它身上无疑是会花费大量时间的，因此我们得认真观察图形，结合我们所学的二次函数的图象特征来分析它：

第一个要关心的是它的开口方向，由图中可知，此时开口向上，顶点在第三象限，想像一下函数开口变大，那么a值应该变小，最小可以变成多少呢？当a值小到接近0时，二次函数图象会接近一条直线（经过上述那两个已知点），顶点若在这条直线下方，那么开口方向就不再向上了，而变成向下，此时顶点就不在第三象限了；继续刚才的想像，开口变小，那么a值应该变大，最大能变成多少呢？当a值变大时，其对称轴会接近y轴，顶点也接近y轴，由于第三象限的限制，故此它的顶点最多只能接近(0，-2）。

基于以上两个数形结合的动态想像(此时不宜演示给学生看动画），开始我们的解析：将函数解析式化为y=ax2+(2-a)x-2，考虑它变化的两个极限情况，当二次函数成为一条直线(一次函数）时，a=0，解析式为y=2x-2；当顶点在(0，-2）时，2-a=0，a=2，解析式为y=2x2-2；

最后再来看P=a-b+c，这个式子是点(-1，a-b+c）的纵坐标，理解为当横坐标为-1时二次函数的函数值。将x=-1分别代入上面的两个函数解析式，分别计算出P=-4和P=0，所以范围是-4

结语：综上所述，高中二次函数灵活多变，考察点众多，已经成为高考考察的重点，因此学生应该予以重视，并从函数概念，基础典型题，以及拓展知识入手，强化对知识的吸收与理解，加快学生发展。