非对称代数Riccati方程的一种快速Newton型算法

宋 岩,王小利,钟瑞华

（闽南师范大学数学与统计学院,福建漳州363000）

本文考虑如下来源于中子运输理论的非对称代数Riccati方程：

其中X∈ℝn×n是未知矩阵,O是零矩阵,已知矩阵Α=Δ-eqT∈ℝn×n,B=eeT∈ℝn×n,C=qqT∈ℝn×n,D =Γ -qeT∈ℝn×n,且分别是定义在区间[0,1]上的Gauss-Legendre权重和节点.

式(1)可能存在多个解,但只有最小正解(即元素均为正数的矩阵)才具有物理意义[1].本文关注于求解式(1)最小正解的数值算法.Lu[2]在2005年首次将该矩阵方程转化为一种非线性向量方程,并指出只要通过计算向量方程的最小正解,即可得到矩阵方程的最小正解.具体来说,若X∈ℝn×n是式(1)的最小正解,则满足:

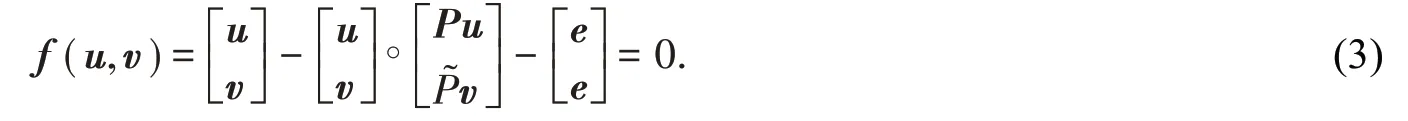
于是通过计算式(3)的最小正解,可以得到式(1)的最小正解.

关于式(3)的数值算法,目前主要有基于不动点迭代的研究,如文献[2-4],及基于Newton 型迭代的研究,如文献[5-11].由于Newton型迭代具有快速收敛性,故得到了广泛的关注.例如,Lu[7]在2005年提出了基于Newton法的一种迭代算法.进一步,Lin等[8]在2008年提出了基于一种三阶收敛的两步Newton法.

本文基于文献[12]所提出的一种具有三阶收敛的两步Newton法,提出了新的计算式(3)的数值迭代算法, 并证明了由该算法迭代产生的向量序列的单调收敛性. 最后, 通过一些数值实验来比较该算法和Newton法以及文献[8]中具有三阶收敛的两步Newton法的计算效能.

1 一种三阶收敛的两步Newton型方法

对于u,v∈ℝn,记x=[uT,vT]T,则式(3)等价于f(x)= 0.给定初始点x0=[uT0,vT0]T∈ℝ2n,考虑如下形式的两步Newton迭代：

其中xk=[uTk,vTk]T,yk=[uˉTk,vˉTk]T.式(4)的标量形式由Frontini和Sormani[12]在2003年将Newton法和文献[13]结合而得到.此外,由式(3)可得f的Jacobi矩阵:

基于迭代格式(4),得到如下用于计算式(3)的两步Newton 型算法.

算法1 一种计算式(3)的两步Newton 型算法选择初始向量u0,v0 ∈ℝn.对于k = 1,2,…,重复以下迭代过程,直至收敛:Step 1.求解关于uˉk,vˉk ∈ℝn的线性方程组:(In - G2(uk)- ZkH1(uk))vˉk = Zkgk - G2(uk)vk - H2(vk)uk +1 2 (vk + vk ∘P͂uk + e),(In - G1(vk))uˉk = H1(uk)vˉk + gk,其中Ζk = H2(vk)(In - G1(vk))-1,gk=1 2 (uk + uk ∘Pvk + e)- G1(vk)uk - H1(uk)vk.Step 2.求解关于uk + 1,vk + 1 ∈ℝn的线性方程组:(In - G2(uˉk)- Ζˉk(H1(uˉk))vk + 1 = Ζˉkgˉk - G2(uˉk)vk - H2(vˉk)uk + vk ∘P͂uk + e,(In - G1(vˉk))uk + 1 = H1(uˉk)vk + 1 + gˉk,其中Zˉk = H2(vˉk)(In - G1(vˉk))-1,gˉk = uk ∘Pvk + e - G1(vˉk)uk - H1(uˉk)vk.

在初始向量u0,v0∈ℝn满足一定条件时,可得到由上述算法迭代产生的向量序列单调收敛于式(3)的最小正解.该收敛性分析将在下一节给出.

2 算法的单调收敛性分析

对于任意的矩阵A,B∈ℝm×n,A∘B=(aijbij)m×n表示A和B的Hadamard 内积. 若对i= 1,2,…,m,j=1,2,…,n,有aij≥bij(aij＞bij),则记A≥B(A＞B);若aij＞0(aij≥0),则称A是正矩阵(非负矩阵).如果一个向量的所有分量都是正(负),我们称它为正(负)向量.如果矩阵A的所有非对角元素都是非正的,则称实方阵A是Z-矩阵.Z-矩阵A可以表示成A=sI-B,其中s∈ℝ,B≥O,I是n阶单位矩阵.若s＞ρ(B),则称Z-矩阵A是非奇异矩阵,其中ρ(B)是B的谱半径.

引理1[8]A∈ℝn×n是一个Z-矩阵,则以下条件等价:

1)A是非奇异的M-矩阵;

2)A-1≥O;

3)若Av＞0 ∈ℝn,则v＞0.

引理2[8]对∀x,h1,h2∈ℝ2n,有f″(x)(h1,h2)=[hT1LT1h2,hT1LT2h2,…,hT1LTnh2]∈ℝ2n,其中

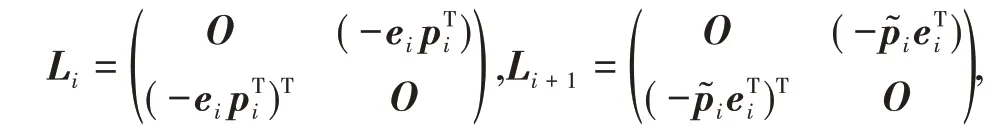
pi和是矩阵P和͂第i列向量.特别地f‴(x)=O,故由Taylor公式有

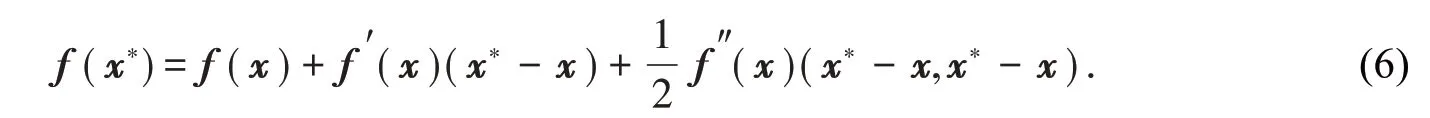
引理3[7]对任意h,h1,h2∈ℝn{0},且h1＜h2,则

引理4[7]若ρ(G(x∗))≤1,则f′(x∗)=I2n-G(x∗)是M-矩阵,其中G(x)由式(5)定义.此外对任意x满足0 ≤x＜x∗,f′(x)是非奇异的M-矩阵.

引理5对∀v1,v2,u1,u2∈ℝn,记x=[u1T,v1T]T,y=[u2T,v2T]T,若v1≤v2,u1≤u2,则f′(y)≤f′(x).

证明

故

定理记x∗是向量方程f(x)= 0的最小正解,若初始向量x0∈ℝ2n,满足0≤x0＜x∗,且f(x0)＜0,则由算法1迭代产生的向量序列{xk}k≥0和{yk}k≥0有定义,且有以下结论:

a)f(xk)＜0,k≥0;

b)0≤xk＜yk＜xk+1＜x∗,k≥0;

证明利用数学归纳法证明a)和b).当k= 0 时,利用式(4)及引理1-4 易得a)和b)成立.假设k=l时,a)和b)成立,下面考虑k=l+ 1的情形.由式(4)和引理5有

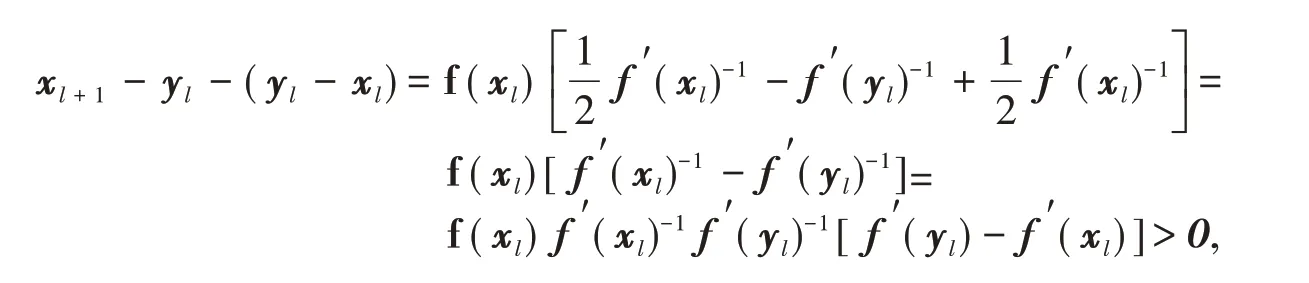
即xl+1-yl＞yl-xl.进而,由引理3得

故由式(6)得

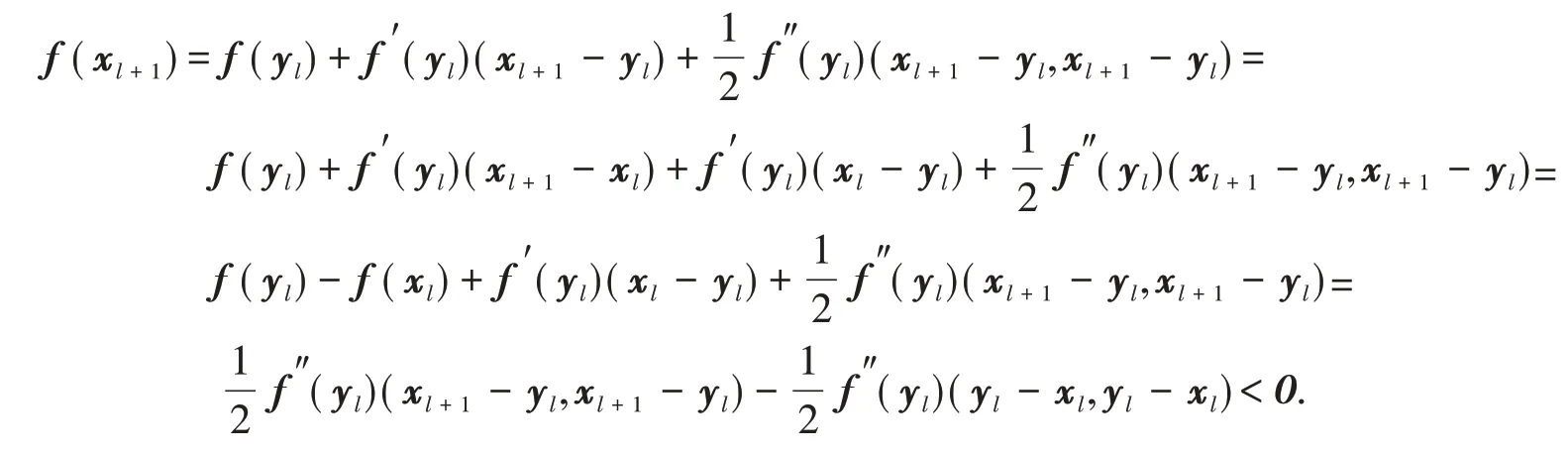
故当k=l+ 1时,f(xl+1)＜0,即a)成立.

对于b),由式(4)和式(6)得

则

得yl+1＜x*,故由引理4知f′(yl+1)是非奇异的M-矩阵,从而由引理1得f′(yl+1)-1＞O.当k=l+ 1时,由式(4)得xl+1＜yl+1,xl+1＜xl+2.由式(6)得及引理5得

进而由式(4)和式(6)得

注意到f′(yl+1)是非奇异的M-矩阵,故由引理1知xl+2＞yl+1.于是由式(4)和式(6)得

即x*-yl+1＞yl+1-xl+1,则由引理3知

由式(4)和式(6)得

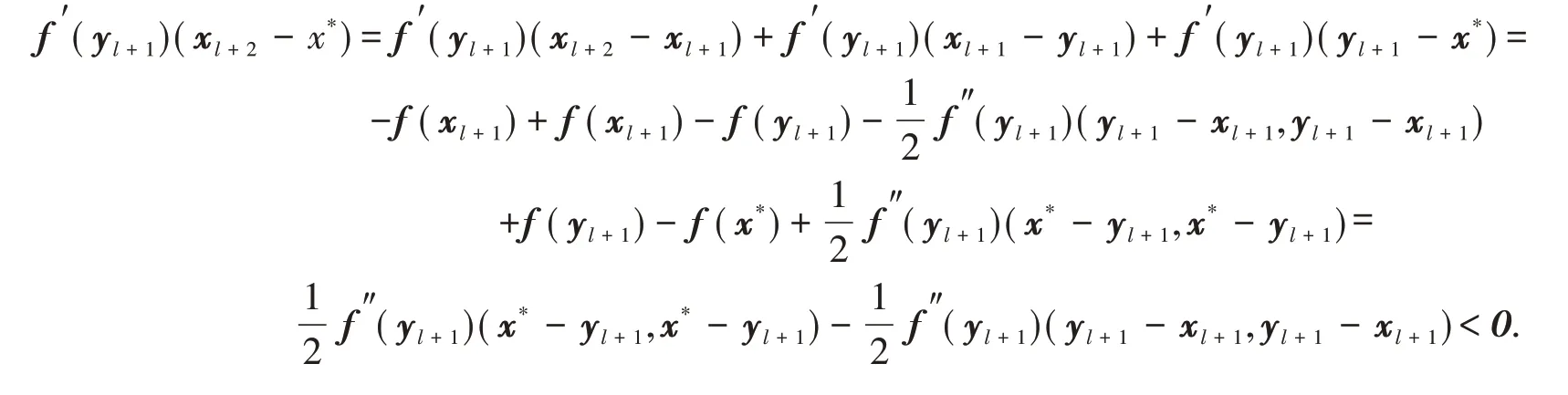
则

故xl+2＜x*.由此可知,当k=l+ 1时,b)成立.因此,对任意k≥0时,a)和b)都成立.

3 数值实验

本节通过一些数值实验来比较算法1(记为TSNM)和文献[7]中的基于Newton 法(记为NM)以及文献[8]中的三阶收敛的两步Newton 法(记为MNI)的计算效能.分别选取(α,c)=(10-7,1 - 5×10-7)和(α,c)=(0.3,0.7)进行测试,在每个测试中,给出迭代次数(记为IT)和相对残差(记为ERR).

维数n分别取512,1 024,2 048,4 096,节点ci和权重ωi,i= 1,2,…,n,从区间[0,1]作数值积分得出.具体步骤,将区间[0,1]分为n4个长度相等的区间,并对每个区间应用Gauss-Legendre 四点求积公式.

我们选取初始点u0=v0=0∈ℝn,算法终止的条件是

其中eps = 2-52≈2.2204×10-16,范数取无穷范数, 所有实验均在CPU - 2.30GHz（Intel(R)Core(TM)i5-6200），RAM - 4GB环境下进行,MATLAΒ版本为2018b.数值实验结果如下表1-表2所示:

表1 α = 0.3,c = 0.7 时的数值模拟Tab.1 The numerical result for α = 0.3,c = 0.7

续表1

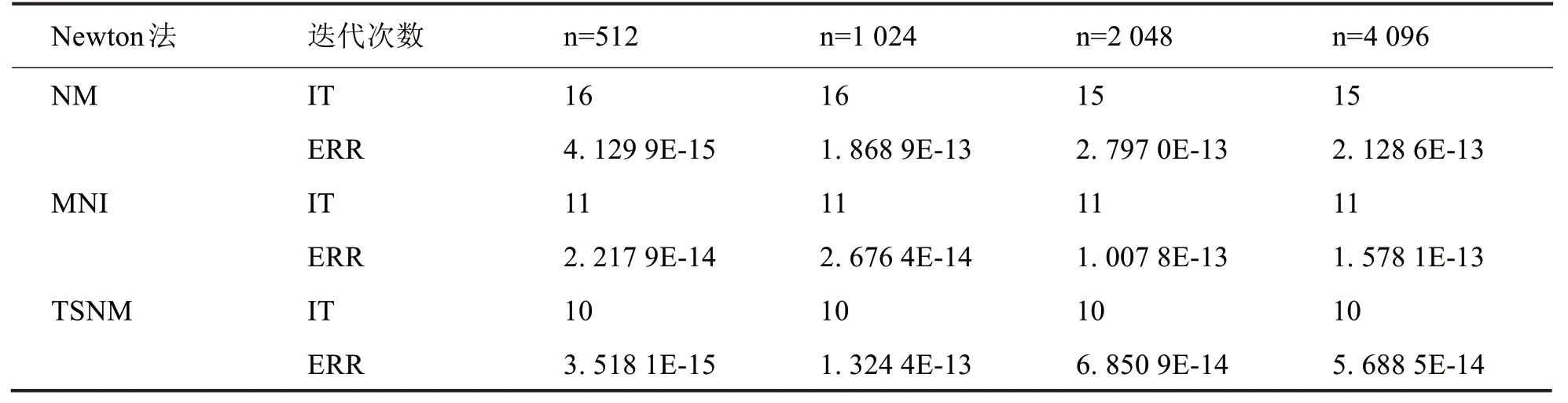
表2 α = 10-7,c = 1 - 5×10-7 时的数值模拟Tab.2 The numerical result for α = 10-7,c = 1 - 5×10-7

从以上数值实验结果可以发现TSNM 法也适用于接近奇异的情况,并且无论n取512,1 024,2 048还是4 096,TSNM 法比NM 法和MNI法的迭代次数少,残差更小.因此,可以认为TSNM 法在求式(3)的最小正解的问题上更优于NM法和MNI法.

图1-图2 是固定n取4 096,(α,c)为(0.3,0.7)和(10-7,1 - 5×10-7)的TSNM 法,NM 法和MNI 法收敛过程.由图可知,在非奇异与接近奇异的情形下,TSNM 法的收敛速度都比Newton法和MNI法更快,特别是接近奇异时,优势更明显.

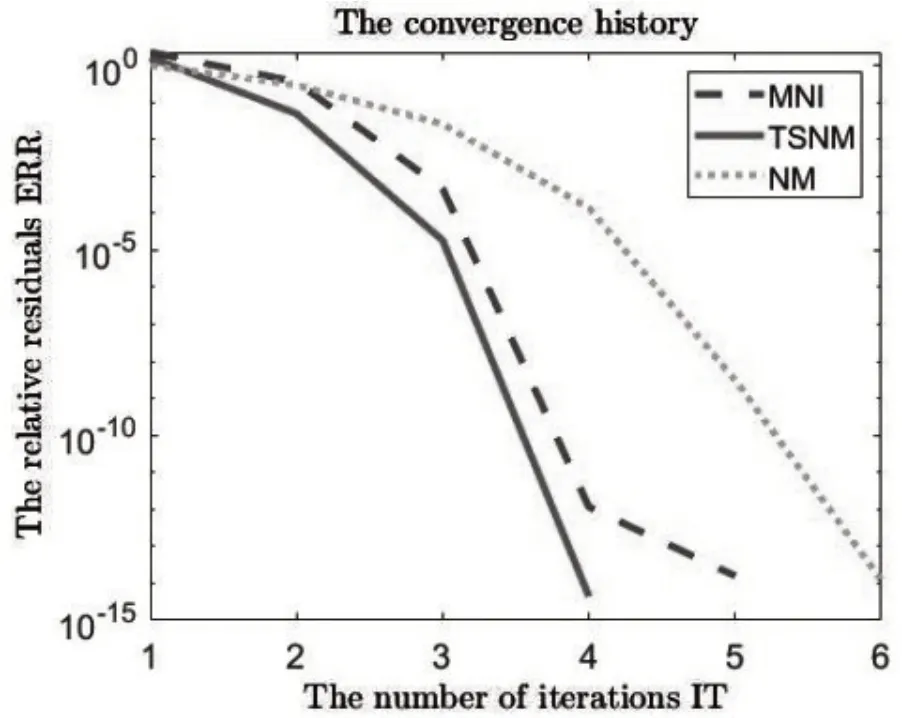
图1 α = 0.3,c = 0.7,n = 4 096Fig.1 α = 0.3,c = 0.7,n = 4 096

图2 α = 10-7,c = 1 - 5×10-7,n= 4 096Fig.2 α = 10-7,c = 1 - 5×10-7,n = 4 096