间歇控制实现混沌同步及图像保密通信

邱文兰,郑 斌,2,蔡建平

（1.闽南师范大学数学与统计学院,福建漳州363000;2.上海大学力学与工程科学学院,上海200072）

随着网络技术和计算机技术的飞速发展,数字图像作为网络传播的载体,其安全性越来越重要.然而,传统的加密算法由于数据量大、冗余、二维空间分布和能量分布不均匀等原因,不适合于数字图像加密.超混沌系统对初值敏感,具有复杂的非周期特性,密钥空间大,是一种自然的信息隐藏载体.与混沌系统相比,它更具有不可预测性,因此,它在图像保密通信中的潜在应用引起了学者们的广泛关注[1-3].而混沌同步的实现,更是保证了混沌保密通信的实时性,具有很高的实用价值,因此,将超混沌系统的特性和混沌同步应用到图像保密通信中,将能够大大提高图像保密通信系统的安全性.

1990年Pecora等[4]首次从理论和电路实现混沌同步后,研究人员提出了多种混沌同步控制方法,如线性反馈控制、脉冲控制、自适应控制、间歇控制、正弦误差反馈控制等[5-9].间歇控制作为一种不连续的控制方法,通过在某些特定的时间段,在系统中加入一定强度的控制量来改变系统的状态,以实现混沌系统的同步.相对连续控制而言,不仅能够减少信号被跟踪和复制的风险,使得加密信息即使被窃取后也会因密钥的“支离破碎”而难以破译,而且它的抗噪声和抗攻击能力更好,所需的数据传输量更少、安全性更高,因此,更加适用于混沌保密通信[10-12].

目前,基于混沌复杂性和混沌同步,已有学者建立了多种合理有效的混沌保密通信方案,为今后混沌保密通信方案在电路和计算机网络中的实现提供了一定的理论依据[13-17].但据我们所知,基于不连续同步控制方法的图像保密通信方案的研究很少,大部分方案是以连续同步控制方法为基础或者只停留在简单信号的加密而不是图像加密[15-17].受这些文献的启发,本文提出了一种基于超混沌系统的同步和间歇控制方法的新型彩色图像加密方案.与上述文献相比,本文通过间歇控制实现超混沌系统的同步的条件更简单,并将该同步方案应用到了图像保密通信中,利用间歇控制下不连续的信号加载来进行信息传输,使得无密钥者无法截取完整的信息,以此来提高图像加密的安全性.最后,数值仿真结果表明,该方案具有较强的密钥敏感性和良好的抗统计分析能力.

1 同步框架

考虑如下的超混沌系统[18]:

其中x1,x2,x3和x4是状态变量,当a=10,b=28,c=和f2=1时,该系统为超混沌系统.

令x(t)=(x1(t),x2(t),x3(t),x4(t))T∈R4,将式(1)改写如下:

其中

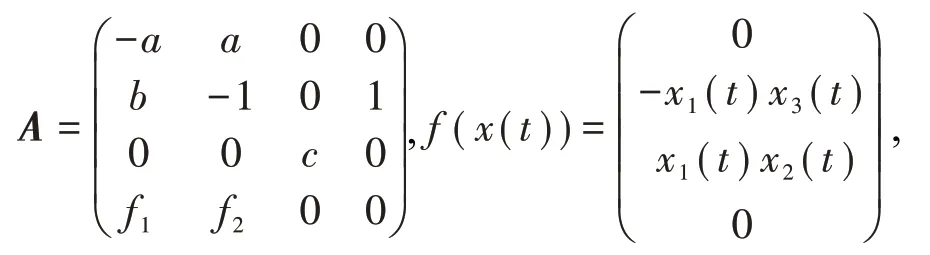
将式(2)作为驱动系统.构造如下的响应系统:

其中y(t)=(y1(t),y2(t),y3(t),y4(t))T∈R4是响应系统的状态变量.非线性函数f(⋅)满足

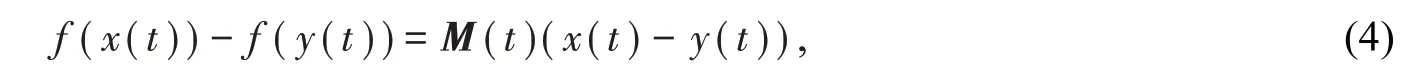
其中

设计如下的间歇控制器u(t):

其中n= 0,1,2,3,…,K=diag{k1,k2,k3,k4},ki＞0,i= 1,2,3,4 是耦合系数,T＞0 是控制周期, 0 ＜h＜1 是控制率.令e(t)=x(t)-y(t)表示误差变量,得到同步误差系统如下:

定义1若式(2)和式(3)的状态变量误差满足

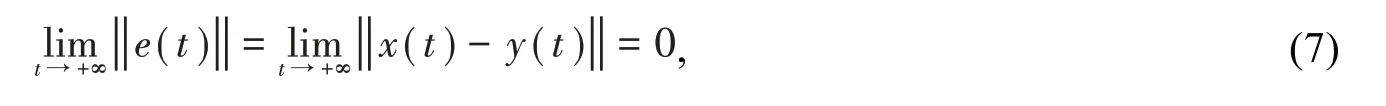
定理1假设式(2)和式(3)的状态变量xi和yi满足 ||xi＜mi,||xi-yi＜d,i= 1,2,3,4,其中mi(i= 1,2,3,4)和d均为正常数. 对于矩阵B(t)=A+AT+M(t)+MT(t), 存在常数λ0和λ1, 使得对任意的t≥0, 有λmax(B(t))≤λ0,λmax(B(t)- 2K)≤λ1, 其中λmax( ∙)表示矩阵的最大特征值. 如果控制率h和耦合系数ki(i= 1,2,3,4)满足以下条件：

那么,式(2)和式(3)可以达到完全同步.

证明选取Lyapunov函数V(e(t))=eT(t)e(t),则式(6)对时间的狄尼导数为：

令B(t)=A+AT+M(t)+MT(t)=(bij(t))4×4,bij(t)=bji(t),i= 1,2,3,4,则

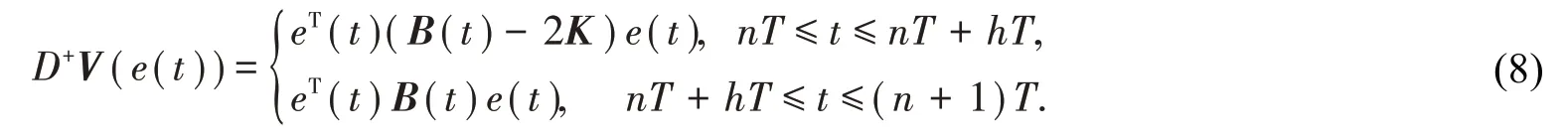
其中B(t)的所有元素bij(t)和特征值都是有界的,设bij(t)的界为bij,即||bij(t) ＜bij.对于任意的t≥0,存在一个常数λ0,使得λmax(B(t))≤λ0,其中λmax(⋅)表示矩阵的最大特征值.假设存在一个常数λ1,使得对任意的t≥0,有λmax(B(t)- 2K)≤λ1.则由式(8)可得:

根据圆盘定理[19]及文献[9]中的讨论可得,只要选择合适的控制率h使得hλ1+(1 -h)λ0＜0 和控制增益ki使得则可使得式(2)和式(3)能够实现完全同步.根据混沌吸引子的有界性,假设超混沌系统的状态变量 ||xi＜mi, ||yi＜mi,i= 1,2,3,4,从而有

至此,完成了定理1的证明.

2 图像保密通信方案

通过间歇控制实现超混沌系统同步的基础上,将该同步方案应用于图像保密通信.与现有的基于混沌的图像保密通信方案类似,图像信号的初始处理需要依赖于超混沌系统的初值敏感性和密钥空间大的特性.即使图像信号数据量大,且具有二维空间分布和能量分布不均匀的特点,由超混沌系统产生的超混沌序列也很容易对其进行掩蔽,产生新的加密信号.然而,在传输过程中,一旦加密后的信号被完全截获,解密者就可以利用各种攻击手段获取原始图像信号.因此,如何传输加密后的信号,使其他人无法从中获得完整而有用的信息是本方案的重点.

本方案中,在间歇控制下加密信号只在无控制时间内传输.由于图像信号数据量大,加密信号不能在一个控制周期内完成传输,使得加密信号的传输是不连续的.因此,在不知道密钥的情况下,截获的有用信息将是“支离破碎”的,难以解密.

2.1 算法设计原理

该算法要求驱动-响应系统首先实现完全同步,因此以下数据均是在系统实现同步后生成的.

在发送端,我们首先对超混沌序列进行了改进以提高保密通信的安全性.当nT≤t≤nT+hT时,式(2)的部分信号xt(t)作为同步信号传输到有控制窗口.当nT+hT≤t≤(n+ 1)T时,式(2)的另一部分信号xc(t)与图像信号m(t)混合得到加密信号c(t),并传输到无控制窗口.无控制窗口和有控制窗口的信号通过公共信道传输到接收端.

在接收端,当nT≤t≤nT+hT时,利用从发送端的有控制窗口传输过来的同步信号xt(t)实现驱动-响应系统的同步.当nT+hT≤t≤(n+ 1)T时,利用式(3)中改造后的部分信号yc(t)对从无控制窗口传过来的加密信号c(t)进行信号分离,得到原始图像信号m͂(t).其保密通信方案和时间帧结构的框图如图1和图2所示.

图1 混沌图像保密通信方案Fig.1 Chaotic image secure communication scheme

图2 时间帧结构Fig.2 Time frame structure

2.2 算法步骤设计

2.2.1 加密

步骤1：为了方便后续的加密,我们先将彩色图像分成三个M×N的矩阵R,G,B.

步骤2：利用四阶龙格库塔法,我们可以得到由驱动系统产生的四个伪随机序列{Xi} ,i= 1,2,3,4.

步骤3：为了提高序列{Xi} 的随机性,,对它进行以下处理,得到四个新的序列{Xi*} .

其中max{Xi} 和min{Xi} 分别表示序列{Xi} 的最大值和最小值,abs(Qi)表示Qi的绝对值,floor(abs(Qi))表示取小于或等于abs(Qi)的最大整数.

步骤4：由于系统的同步需要时间,而加密和解密的实现需要在系统达到同步的前提下进行.因此,我们不能直接利用{Xi*} 来加密图像信号.假设同步时间为tsyn秒,则只取时间tsyn秒后产生的超混沌序列来进行后续的混沌同步和图像加密,我们将tsyn秒后产生的信号记为{Xisyn} ,i= 1,2,3,4.若步长取0.001,则表示1秒就有1 000个{Xi} 中的数据产生.因此,由下面的公式可以得到{Xisyn} .

步骤5：选取合适的控制率h,然后我们只取{Xisyn} 中的前三个序列,即X1syn,X2syn,X3syn.在每1 秒中,每个序列的前1 000×h个数据作为同步数据xit(t),i= 1,2,3,后1 000×(1 -h)个数据作为与图像信息混合的遮掩信号xic(t),i= 1,2,3,具体操作如下：

假设系统的运行时间为τ秒,τ= 1,2,3,…,k,那么第k秒的xikt和xikc如下：

其中Xisyn(n:m)表示选取序列{Xisyn} 中第n到第m个数据.通过式(13)和式(14)可以得到xit和xic.

步骤6：为方便后续的加密,取xic,i= 1,2,3中每个序列的前M×N个数据,分别用矩阵P,C,E来表示.

步骤7：在间歇控制下,xit(t)在时间nT≤t≤nT+hT内传输到有控制窗口并通过公共信道传输到接收端的有控制窗口, 以此来实现驱动-响应系统的同步. 当nT+hT≤t≤(n+ 1)T, 图像信号R,G,B则与P,C,E混合得到加密信号R1,G1,B1,并通过公共信道传输到接收端的无控制窗口.

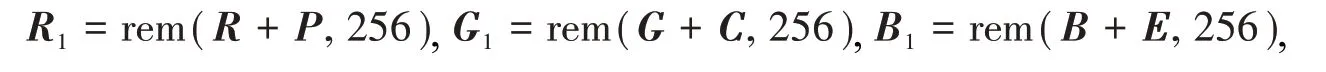
其中rem(a,b)表示取模运算.

2.2.2 解密

步骤1：在接收端，利用间歇控制实现驱动-响应系统的同步.

步骤2：同样选择同步后的数据，并按照加密方案中的步骤3-步骤6对所选数据进行同样的处理.

步骤3：对处理后的数据作如加密方案中的步骤7的逆运算,得到原始图像信号.

2.3 数值仿真

选择512×512 的Lena 图作为要加密的图像,若式(2)的初值取X0=[1.2,0.3,-1,2.4 ],式(3)的初值取Y0=[-1.6,-1.4,1.2,0.6 ],控制率取0.6,步长取0.001,可以得到式(2)和式(3)的同步时间约为tsyn=2.8 s.利用MATLAΒ对上述保密通信方案进行数值仿真,得到图像加密解密的模拟结果如图3所示.结果表明,经过加密并解密后的图像没有失真.

图3 图像加密解密的模拟结果Fig.3 Simulation results of image encryption and decryption

3 安全性分析

3.1 密钥敏感性分析

本文将式(2)的初始值X0=[1.2,0.3,-1,2.4 ]作为图像保密通信方案的密钥. 若将密钥改为：[1.200 000 000 1,0.3,-1,2.4 ],利用该密钥对加密图像进行解密,得到对应的解密后的图像如图4所示.

图4 利用改变后的密钥解密的图像Fig.4 Image of decryption using the changed key

对密钥的其余三个位置作类似的细微改变,结果均表明,当驱动系统的初始值有细微改变时,都无法将加密图像还原为原始图像,说明密钥具有高度敏感性.

3.2 NIST检测

在混沌图像保密通信方案中,混沌系统产生的伪随机序列的随机性显得尤为重要.NIST提供了对随机性的必要测试,包括频率、块频率等16 个主要项目.随机性通常用概率方法进行检验,结果由检验P 值决定.如果P 值大于显著性水平0.01,则表明序列是随机的.我们将2.2.1 小节中所用到的序列1,2,3 转化为二进制,然后对其进行NIST 检测,结果如表1 所示.由表1 我们可以看到,该序列的P 值均大于0.01,通过了NIST的所有测试.

4 结论

本文研究了一种新的基于超混沌系统的超混沌序列和间歇控制同步的彩色图像加密方案.本方案的优点在于通过超混沌系统良好的混沌特性和间歇控制下加密信号传输的不连续性来使得窃密者无法截取完整的加密信息,一定程度上提高了图像加密的安全性.此外,用Lena 图像作为数值仿真的一个例子,利用该方案实现了对图像的加密和解密,且解密得到的图像没有失真,说明该方案具有可行性.最后,利用密钥敏感性分析和NIST检测进行安全性分析,结果表明该方案具有良好的加密效果和较高的安全性.

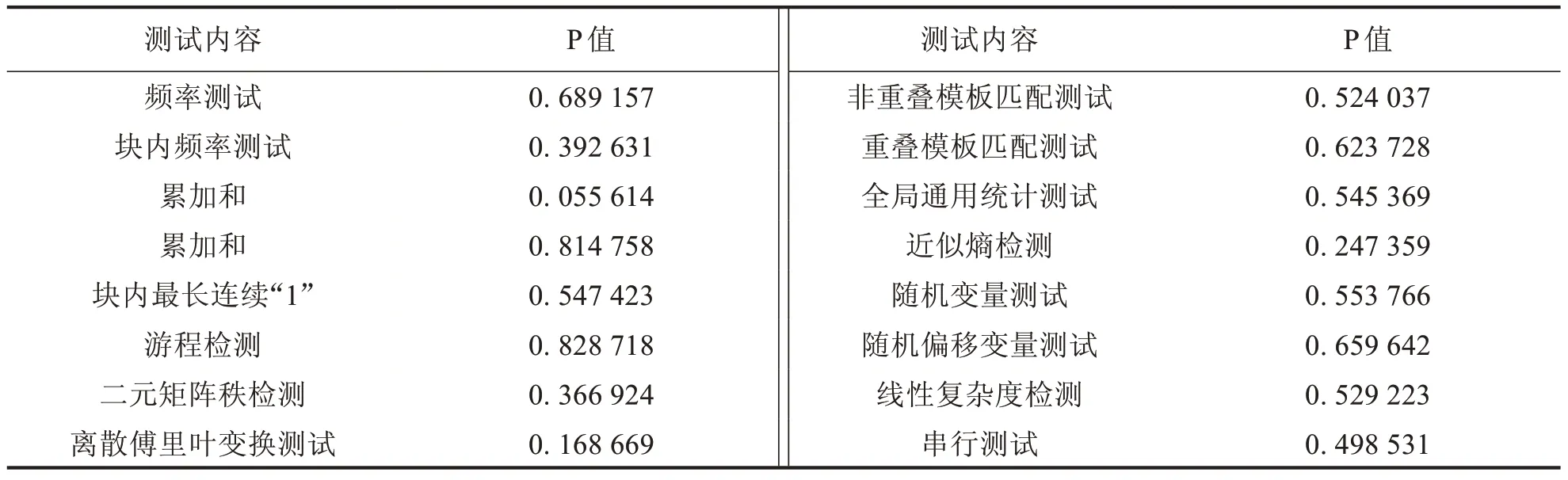
表1 NIST检测结果Tab.1 The results of NIST test