Equal-Width波方程的高精度守恒差分格式

钟瑞华,程宏，何育宇

（闽南师范大学数学与统计学院,福建漳州363000）

1984年，Morrison 等[1]提出了Equal-Width 波方程，该方程多应用于模拟一维波在具有色散过程的非线性介质中的传播.随后,许多人对该方程进行了大量的研究.Gardner 等[2]用三次Β-样条有限元方法模拟了电子束发射过程中孤立波的迁移和相互作用.Zaki[3]用Petrov-Galerkin 方法求解修正的Equal-Width方程,并使用五次Β-样条有限元模型模拟孤子的产生、运动和孤立波的相互作用.Abdulkadir[4]采用线性Galarkin 有限元方法对Equal-Width 波方程进行了研究. Rui[5]利用平面动力系统分支理论方法研究了Equal-Width 波方程的孤波解和周期解.

本文考虑如下Equal-Width波方程的初边值问题

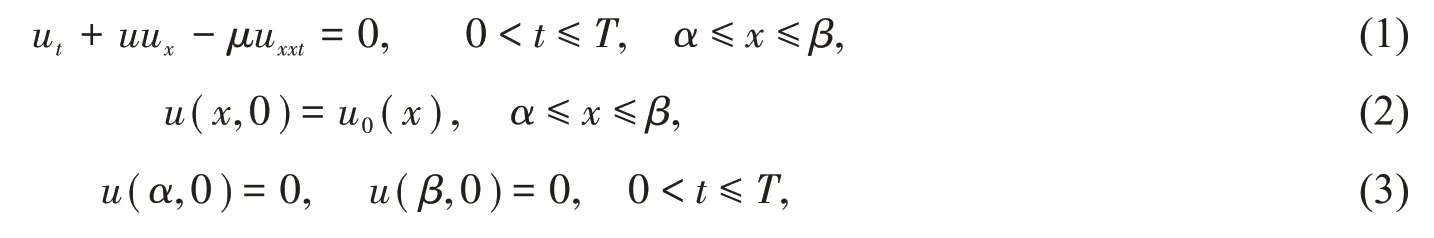
其中μ是给定的正常数.可以验证,式(1)-式(3)具有如下守恒律

首先建立式(1)-式(3)的三层线性差分格式,在时间上和空间上分别达到二阶和四阶精度,并证明所建立的差分格式的守恒性、收敛性和稳定性,数值结果验证了理论分析的可靠性.

1 差分格式的构造

对求解区域[α,β]×[0,T]进行网格剖分,取空间步长h=(β-α)/J,时间步长τ=T/N,其中J、N为正整数,记网格点xj=α+jh(0 ≤j≤J),tn=nτ(0 ≤n≤N).记

对任意un、vn∈定义如下记号[6]：

对式(1)-式(3)考虑如下差分格式：

其中

式(6)-式(8)可展开为一个五对角矩阵的线性方程组,可用“追赶法”求解.

由于式(6)-式(8)是三层线性隐式格式,所以需要下面的两层格式来计算u1

2 差分格式的守恒性

引理1[7]对任意的un、vn∈,则

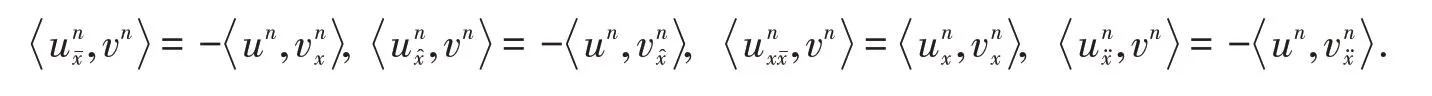
当un=vn时,有

引理2[7]对任意的un∈,则

引理3[7]对任意的un∈则有

引理4[7](离散Sobolev不等式)对任意的un∈Z0h,存在两个正常数a和b,使得

定理1设则式(6)-式(8)满足质量守恒和能量守恒,即

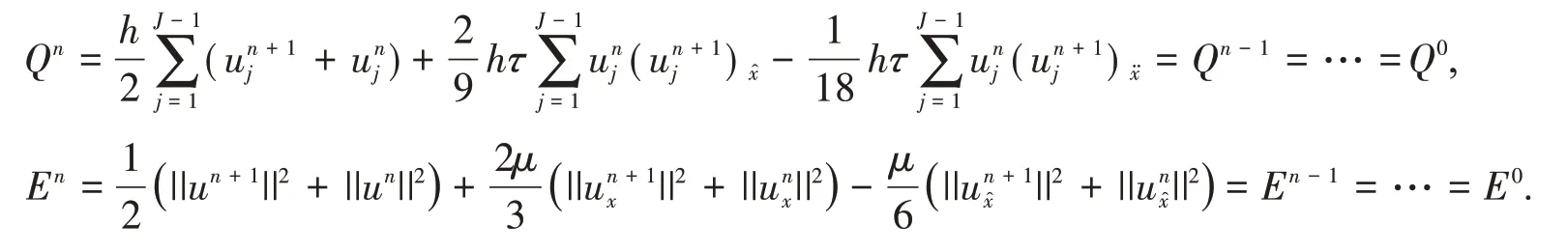
证明将式(6)两端同时乘以h后对j从1到J- 1求和,根据边界条件,得

即

由Qn的定义,对上式的n递推即可得Qn=Qn-1= …=Q0.

将式(9)与2uˉn作内积,由引理1可得

由En的定义,对式(10)的n递推即可得En=En-1= …=E0.

3 差分格式解的存在唯一性和有界性

定理2式(6)-式(8)的解un是唯一存在的.

证明u0由式(7)确定,用C-N格式计算u1,则u0和u1是唯一确定的.设u0,u1,…,un(n≤N- 1)是唯一可解的,考虑式(4)中的un+1,我们有

将式(11)与un+1作内积,又由引理2和引理3得

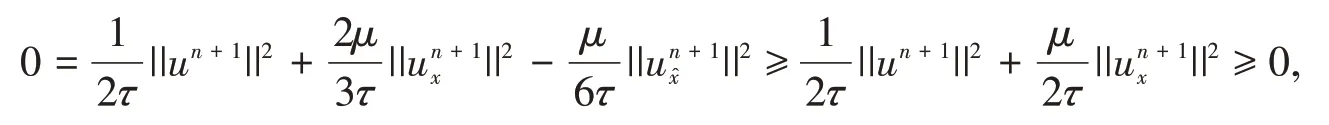
即||un+1||= 0,从而差分格式是唯一可解的.

定理3设则式(6)-式(8)的解满足

证明由引理3和定理1,可得

其中

由于μ是正常数,即||un||≤C,||unx||≤C, 根据引理4,有 ||un||∞≤C.

4 差分格式解的收敛性与稳定性

引理5[7](离散Gronwall不等式)假设{Gn/n≥0} 是非负数列,且满足

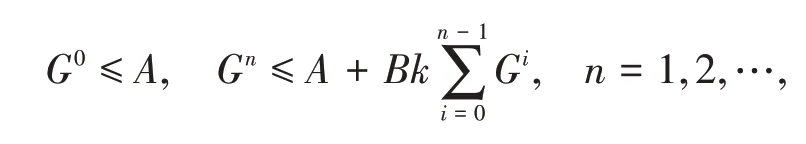
其中A和B均为非负数,则Gn=AeBnk,n= 0,1,2,….

定理4设u0∈H02[α,β],u(x,t)∈C6,3[α,β],式(6)-(8)的解un依L∞范数收敛到式(1)-式(3)的精确解,并且收敛阶为O(τ2+h4).

证明令en=Un-un,则式(6)-式(8)的截断误差为

将式(12)与2eˉn作内积,由引理1得

根据引理3及定理3,可得

同时,有

同理,有

将式(14)-式(16)代入式(13),可得

令

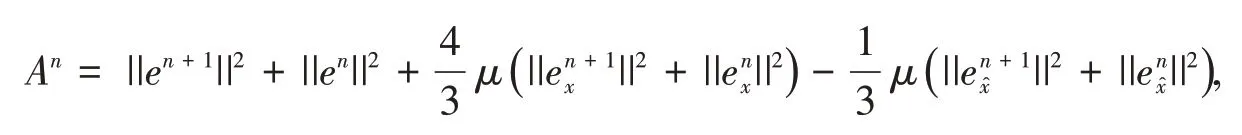
将式(17)从1到n累加,有

其中τ,C是正常数,根据An的定义和引理3,有

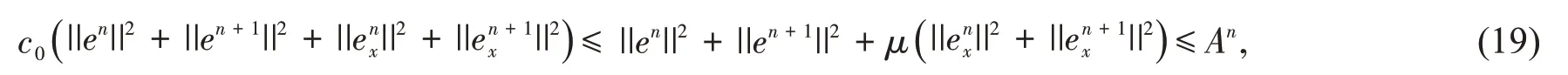
其中c0= min(1,μ).由式(18)-式(19)得

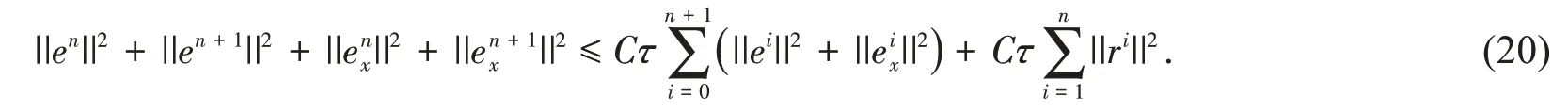
令Gn= ||en||2+ ||en+1||2+ ||enx||2+ ||enx+1||2,则式(20)可以写成其中

从而

式(21)可以写成

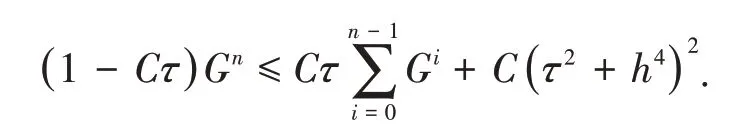
对于τ足够小,即1 -Cτ＞0,有

根据引理5,得

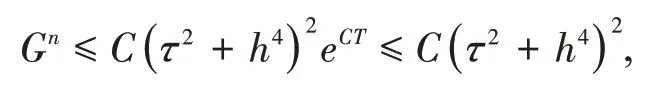
即有||en||≤C(τ2+h4),||enx||≤C(τ2+h4).由引理4,可得||en||∞≤C(τ2+h4).定理得证.

5 数值实验

为验证式(6)-式(8)的守恒性和稳定性,选取以下模型问题[8]：

初始条件为

已知式(22)-式(23)的精确解为

设

其中Ujn=u(xj,tn)为精确解,un

j为式(6)-式(8)的数值解,定义时间和空间的收敛阶为

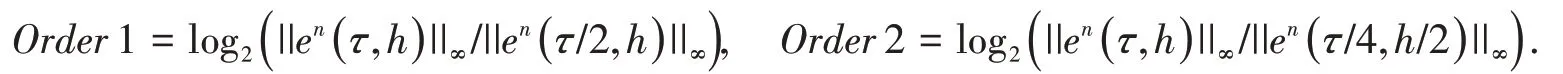
取γ=0.1,μ= 1,α=- 20,β=30,T=1,x0= 10，分别取h= 0.1,τ= 1 和h= 0.05,τ= 1对式(6)-式(8)进行计算,不同时刻的数值解分别见图1(左)和图1(右).表1 验证了格式在时间上具有二阶收敛精度,表2 验证了格式在空间上具有四阶收敛精度,表3 验证了格式的质量和能量守恒性.以上结果表明所建立的差分格式(6)-式(8)是可靠和有效的.

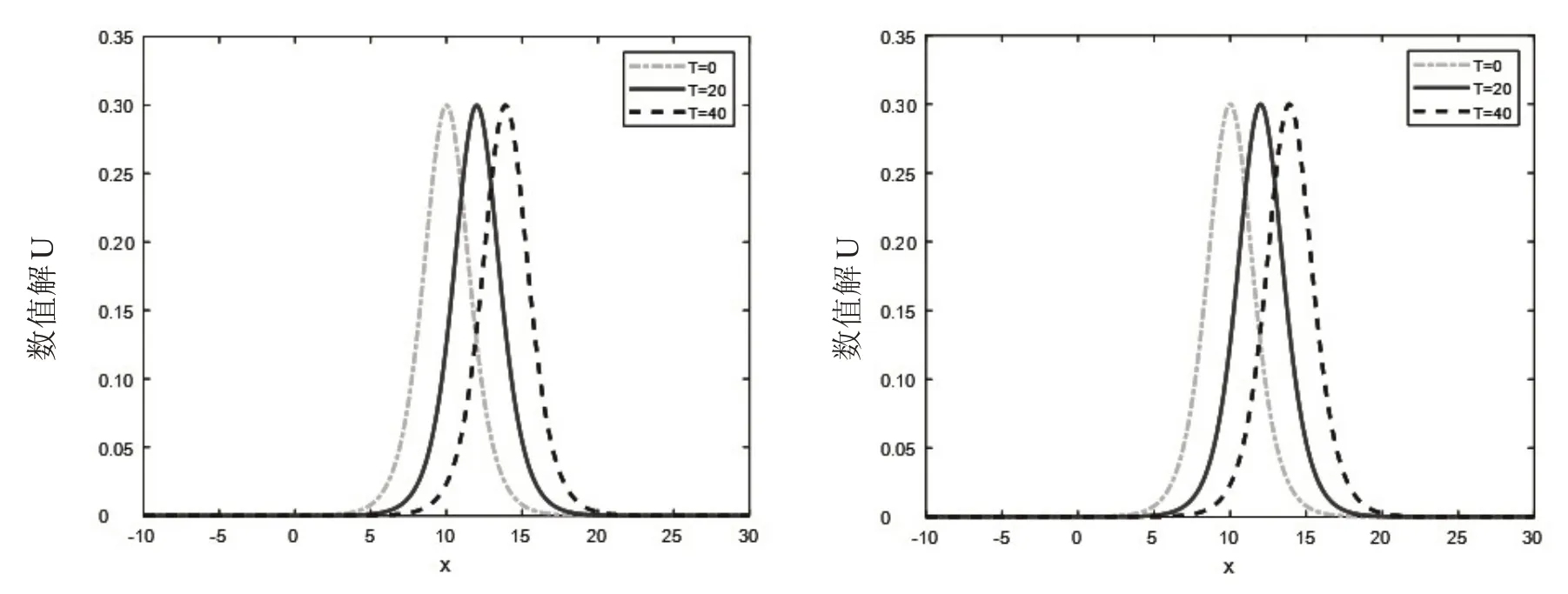
图1 h = 0.1,τ = 1(左)和h = 0.05,τ = 1(右)时不同时刻的数值解Fig.1 Numerical solution at different times with h = 0.1,τ = 1(left)and h = 0.05,τ = 1 (right)

表1 h = 0.05 和T=1时的误差和时间收敛阶Tab.1 Errors and temporal convergence orders with h = 0.05 and T=1

表2 τ = h2 和T=40时的误差和空间收敛阶Tab.2 Errors and spatial convergence orders with τ = h2 and T=40

表3 h = 0.25 和h = 0.5 时,不同T 下的守恒量Tab.3 The conserved quantities at different T with h = 0.25 and h = 0.5