基于复杂网络核心体的控制方法

王媛媛，袁正中,2，赵 琛

（1.闽南师范大学数学与统计学院，福建漳州363000；2.数据科学与统计福建省高校重点实验室，福建漳州363000；3.河北师范大学计算机与网络空间安全学院，河北石家庄050024）

生活中随处可见的生物网络[1]、交通网络[2]、社会网络[3]、信息网络[4]等都称为复杂网络.它们不仅拥有超大的网络规模，而且包含丰富的结构特性[5]和动力学特性，如同步、涌现等[6-8].目前，研究人员在复杂网络的传播[9]、搜索[10]、同步[11-12]、控制[13]等方面已经取得了非常重要的成果.然而，网络的复杂性仍然给这些领域的研究工作带来了诸多挑战[14].其中，复杂网络乃至各种复杂系统是否可控、如何精确控制等问题已成为非常关键且拥有广泛应用价值的问题.

2011年，Liu等[15]首次从线性系统的角度研究复杂网络的结构可控问题，利用Kalman可控理论[16]证明了网络最大匹配中的未匹配节点是使网络可控的驱动节点.但该理论只适用于边权可独立选取的有向网络，在无向复杂网络或给定权重的网络下不适用.随后，Yuan等[17]从邻接矩阵特征值的角度提出了严格可控理论，指出驱动节点数等于对应系统的邻接矩阵特征值的最大几何重数，并且通过对矩阵进行初等变换可以得到具体的驱动节点.特别地，对于稀疏网络，网络的驱动节点数由邻接矩阵的秩决定.然而，复杂网络系统包含成千上万的节点，直接用初等变换的方法寻找控制网络的驱动节点无疑是困难的.

因此，研究者们开始尝试通过节点较少的网络核心去控制整个网络[18-19].特别地，文献[19]利用叶子删除法获得复杂网络的控制核心体，基于PΒH 可控条件证明了对于大部分的网络，控制网络核心体即可完成对整个网络的控制.然而，对于一些网络，仅通过对其核心体实施控制，不能完成对整个网络的控制.

本文基于PΒH 可控理论，针对上述复杂网络实际控制中核心体可控但网络本身不可控的问题，提出两种复杂网络可控方案.一是尝试其它使核心体可控的驱动节点组；二是增加新的驱动节点.推广到一般情形，提出并论证在控制核心体的基础上，对每次删除叶子中度为1 的节点增加控制可以使原始网络可控.最后，重点分析了核心体加链路的网络，证明增加对该链中度为1 的节点的控制可以使整个网络可控.

1 复杂网络可控的基本概念

复杂网络可控是指系统在一定的时间内，经过适当的外界输入作用，从任意初始状态变成最终状态的性质.考虑以下含有N个节点的无向网络动力学系统[15,17]：

其中x=(x1,x2,…,xN)T表示N个节点的状态.A=(aij)∈R N× N为系统的邻接矩阵，其中，aij=aji=1 (i≠j)表示节点i、j之间存在连接；否则aij=0 (包括i=j).B∈R N×M为列满秩的输入矩阵，其中B的列数表示需要独立控制的节点个数.若B不是列满秩矩阵，则说明整个控制系统有多余的控制输入，可以进一步简化[17].向量u=(u1,u2,…,uM)T为M个独立的控制输入.式(1)可控的充要条件为以下PΒH 可控条件成立[20]：

其中λ为矩阵A对应的特征值，IN为N阶单位矩阵.

对于含有叶子的稀疏无向复杂网络，持续地删除网络叶子及其连边并保留孤立节点，直至整个网络不再包含度为1 的节点，最终得到的所有连通集团和孤立节点共同构成网络的控制核心体[19].其中，叶子是指由一度节点、邻居和它们之间的连接构成的结构.

2 主要结果

对于大部分的复杂网络，仅对其核心体实施控制即可实现对整个网络的控制，我们称为可由核心体控制的网络.反之，核心体可控而整个网络不可控，称为不可由核心体控制的网络.下面，我们将针对3 种不可由核心体控制的网络展开讨论.

2.1 一种不可由核心体控制的网络

对于含有N个节点的无向网络，如图1a)所示，前N-2 个节点围成一个环，且节点1 分别与节点2、…、节点N-2 相连，节点N-4 连接一个叶子，经过叶子删除后得到核心体A0(虚线圈起部分).对节点1、2 施加控制，利用PΒH可控条件可知，此时核心体可控(见图1b)).

图1 不可由核心体控制的网络的控制情况Fig.1 The control situation of the network that cannot be controlled by the core

于是

其中

Wind-Solar Complementary Energy Supply Platform Based on Intelligent Beacon

下面分析在该控制输入下，整个网络的可控性.此时的控制输入矩阵记为B.

将矩阵(λIN-A,B)进行一系列的初等变换化为阶梯矩阵如下：

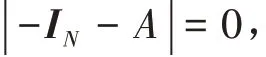
可见，在最后一个矩阵中，除第N-1行之外其余行的非零元素均在不同行不同列.因此，这些行向量是线性无关的.又因为A满足因此-1 是矩阵A的一个特征值.此时，矩阵(-IN-A,B)第N- 1 行的非零元素均可经过一些初等行变换化为零元素.说明rank(-IN-A,B) =N- 1 ＜N恒成立，由PΒH 可控条件可知，在控制节点1，2 的情况下，原始网络不可控.

对于这种不可由核心体控制的网络，可以使用如下两种替代控制方案：

1)更换驱动节点的组合

由于控制核心体的驱动节点不止一组，可以寻找其它驱动节点的组合并验证其可控性.否则，考虑方法二.对于图1a)所示的网络，分别在节点N- 4的两侧各取一个节点，如选取节点2 和节点N- 2，此时新的控制输入矩阵记为B1，通过计算验证可知rank(λIN-A,B1)=N，说明原始网络可控(见图1c)).

这种方法通常适用于节点较少的网络.对于节点比较多、连接复杂的网络，寻找其它驱动节点的组合并不容易，即使可以找到所有驱动节点的组合，但数量过多，验证可控条件的计算量也相应增加.

2）在原有的使核心体可控的控制输入下增加新的驱动节点.对于图1b)所示的网络，在原有两个驱动节点的情况下增加一个新的驱动节点.这里可增加节点N- 3、节点N- 2、节点N- 1或节点N，更新的控制输入矩阵B分别如下：

2.2 一般不可由核心体控制的网络

定理1对于任意不可由核心体控制的网络，在核心体可控的基础上，对每次删除中度为1 的节点增加控制，则原始网络完全可控.

证明不妨以一次删除为例，设包含一个度为1的节点的网络为：

其中，1表示一度节点与其邻居的连接，向量α表示删去的叶子与其余节点的连接情况.矩阵A0表示删除一个叶子后得到的网络.假设A0可以由B0控制，由PΒH可控条件满足：

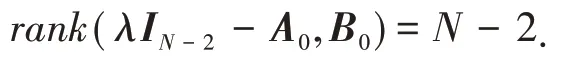
在核心体可控的基础上，再增加对度为1的节点的控制，得到新的输入矩阵B如下：

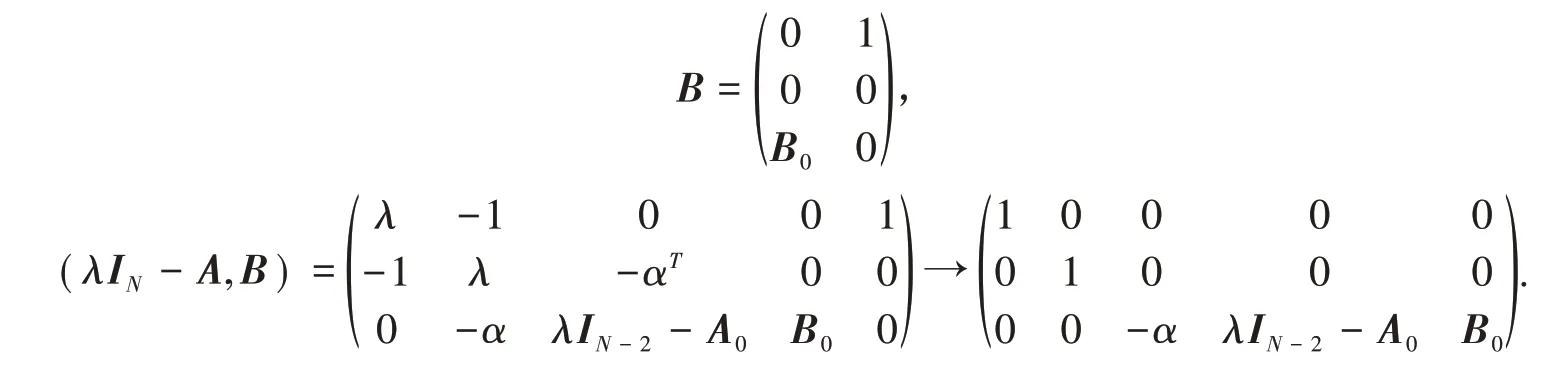
因此

由PΒH 可控条件可知整个网络可控.于是，在核心体可控的前提下，对每次删除时度为1的节点增加控制，原始网络完全可控.

在图2 所示的网络中，节点1、2、3、8 和它们之间的连边构成核心体（虚线部分）.可以验证，控制节点1、2 和8 后，核心体可控，但整个网络不可控.根据定理1，增加控制每次删除中度为1 的节点12，10，7 和5（箭头表示），整个网络可控.

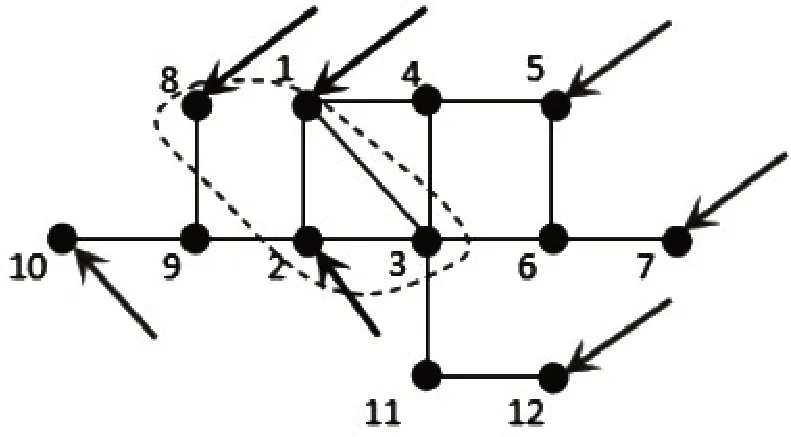
图2 增加对每次删除中度为1的节点的控制使网络可控Fig.2 Add control to the once-deleted node every time,the network is controllable

在已有的控制方法[19]中，需要依次验证每次删除后的邻接矩阵的相关条件是否满足.而定理1免去了大量的计算过程，提供了基于核心体控制网络的一般思路.在实际应用时，每次删除都要增加相应的控制.但在节点较多的网络中，控制输入成本就比较高.因此，对于一类特殊的不可控网络——由核心体和链路组成的无向复杂网络，可以在定理1 的基础上进行推广，将对每次删除中度为1的节点的控制进一步缩减为对整条链路中度为1的节点的控制，从而大大减少控制输入成本.

2.3 一类特殊的不可由核心体控制的网络

定理2对于任意的由核心体和一条连接核心体的链路构成的网络，若仅控制核心体不能控制整个网络.那么，在核心体可控的基础上，仅增加对链路的控制，则原始网络完全可控.

证明不妨设由核心体和一条链路构成的网络A有如下形式，且增加对度为1的节点的控制，则

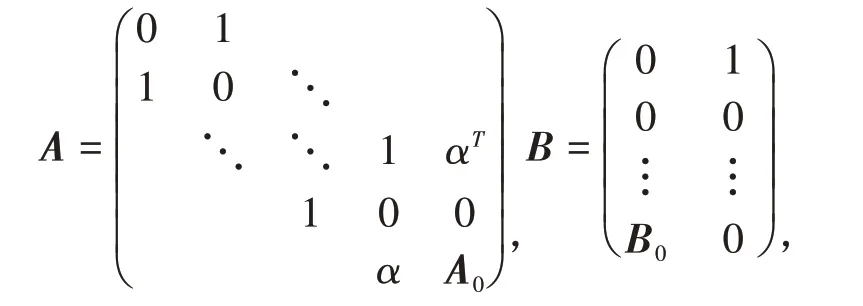
其中，设链路含m个节点，核心体仍记为A0，设A0有n 个节点且可以由输入矩阵B0控制.则由PΒH 可控条件满足：

对于原始网络A有

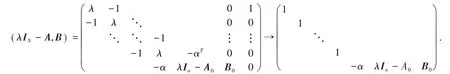
显然，rank(λIN-A,B)=n+m=N，由PΒH可控条件，原始网络完全可控.

上述分析说明在核心体可控的基础上，对链路中度为1 的节点增加控制，整个网络完全可控.该思路可以不必控制每次删除中度为1 的节点，一定程度上减少了控制输入成本.进一步地，该理论同样适用于核心体加多条链路的情形.

定理3对于任意由核心体和多条独立链路构成的网络，若控制核心体不能控制整个网络.那么，在核心体可控的基础上，增加对每条链路中度为1的节点的控制，则原始网络可控.

证明同定理2.

图3a)所示的网络包含核心体（虚线圈起部分）和一条链路.在核心体可控的基础上，仅对该链中度为

图3 增加对每条链路中度为1的节点的控制使网络可控Fig.3 Add control to the one-degree nodes in each link,and the network is controllable

3 结束语

本文研究了核心体可控，但整体不可控的网络控制问题.首先，得到了控制一类特殊网络的方法：更换驱动节点组合或者增加适当驱动节点使网络可控.其次，提出更一般化控制方法：除了原有的对核心体的控制，对网络中每次删除中度为1 的节点增加控制可以使整个网络达到可控状态.最后，重点分析了核心体加链路的网络的控制方法.除了原有的对核心体的控制，对链路中度为1的节点增加控制即可使整个网络可控.这一发现极大地减少了需要增加的驱动节点，提高了控制效率.该研究对于那些由可控网络扩充得到的新网络的控制有着重要意义.1的节点增加控制（灰色箭头表示），此时整个网络可控.图3b)所示的网络包含了核心体和多条链路.在核心体可控的基础上，对每一条链路中度为1的节点增加控制（灰色箭头表示），此时整个网络可控.