基于面向问题概念格的技能约简与推测关系

冯丹露,周银凤

（闽南师范大学数学与统计学院,福建漳州363000）

知识空间理论(Knowledge space theory,简称“KST”)[1]是Falmagne和Doignon于1985年首先提出的一种用数学理论进行教育评估和指导的一种数学心理框架.目前KST在自适应教学与个性化学习[2-4]等领域得到广泛应用.形式概念分析（Formal Concept Analysis,简称“FCA”）[5]是R.Wille 于1982年首先提出的一种从形式背景进行数据规则提取和分析的重要工具,是人工智能研究[6-7]的重要方向.

1996年Rusch等[8]提出知识背景概念,首次提出由知识背景构建知识空间的方法.2010年Spoto等[9]提出技能映射概念,并运用到心理评估上,提出由形式背景构建技能映射在合取模型下诱导知识结构的方法.李进金等[10]提出形式背景与知识空间相互构建的另一种方法.周银凤等[11]提出技能背景的概念,进一步研究知识空间理论与形式概念分析间的联系.

知识状态与知识结构是对学习者进行知识评估和学习指导的主要工具.如何构建学习者的知识状态与知识结构是KST 的核心.知识空间理论研究初期,主要通过有丰富经验的专家来建立知识状态与知识结构.Doignon等[12]基于问题与技能的关系,提出由技能映射和技能多映射构建知识结构的方法.

技能的一个特定子集代表了个人对技能的掌握情况.学习者想要解决某些问题必须要掌握某些相应的技能,故可根据学习者对问题的解答情况来获取其知识状态.不同问题的求解可能与同一技能集相关,于是不同的技能集可能诱导相同的知识状态,故有必要进行技能约简.Doignon[13]提出极小技能集与极小技能映射的概念.高纯等[14]提出求解极小技能集的不同方法.周银凤等[11]提出保持知识基不变的一种技能约简方法.

问题与问题之间可能存在着某种偏序关系,Doignon等[1]将这种关系称为推测关系,推测关系体现了学习者能够解决问题的一个先后顺序.如何准确判断问题之间的推测关系,对评估学习者的知识水平和构建后期学习路径具有重要辅助作用.Falmagne等[12]将推测关系与知识结构相联系,给出了推测关系的一个等价条件.

文献[11]运用形式背景的反背景去建立概念格,获取由技能映射诱导的知识结构,但不够直接.本文在形式背景的正背景前提下,将问题视为对象,技能视为属性,提出一种与文献[11]不同的由技能背景构造知识结构与知识基的方法.首先,通过面向问题（技能）概念格,建立技能背景与知识结构的更直接的联系.其次,给出面向问题概念格的一种技能约简方法,直接获得技能约简集和知识基.最后,基于技能背景,不需要求解知识结构,就可更简单、更快速的确定问题的推测关系,故有必要在技能背景下讨论问题的推测关系.

1 预备知识

1.1 形式概念分析概述

定义1[9]三元组(U,A,I)称为一个形式背景,其中U={x1,x2,…,xn}是对象集,A={a1,a2,…,am}是属性集,I是U×A上的二元关系.若(x,a)∈I,则称对象x具有属性a；若(x,a)∉I,则称对象x不具有属性a.

定义2[9]设(U,A,I)为形式背景,在对象集X⊆U和属性集B⊆A上分别定义运算

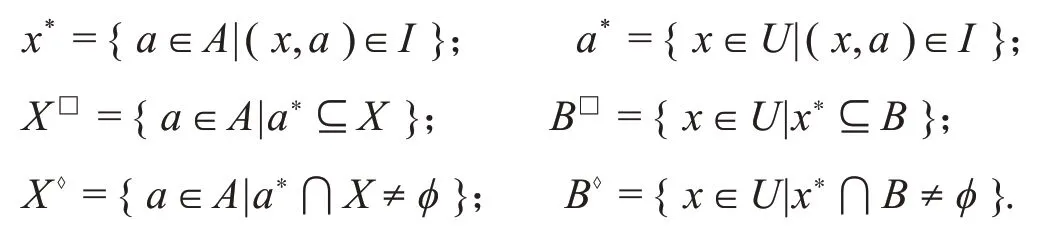
定义3[9]设(U,A,I)为形式背景,若X□=B,B⋄=X,则称(X,B)为面向对象概念；若X⋄=B,B□=X,则称(X,B)为面向属性概念.此时称X为面向对象（属性）概念的外延,B为面向对象（属性）概念的内涵.

用LO(U,A,I)表示形式背景(U,A,I)的全体对象概念,用LP(U,A,I)表示形式背景(U,A,I)的全体属性概念.

定义4[9]设(U,A,I)为形式背景,若X1⊆X2,记(X1,B1)⊆(X2,B2),则LO(U,A,I)与LP(U,A,I)上的偏序关系.

在LO(U,A,I)上定义：

在LP(U,A,I)上定义：

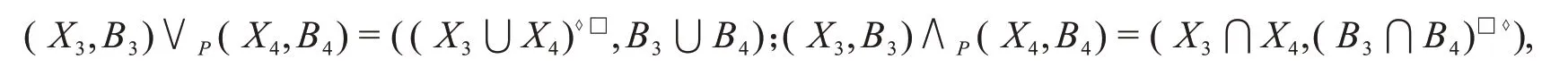
则(LO(U,A,I),∨,∧)与(LP(U,A,I),∨,∧)都是完备格,称LO(U,A,I)与LP(U,A,I)分别为形式背景(U,A,I)的面向对象概念格与面向属性概念格.

1.2 知识空间理论概述

在知识空间理论中,把能够反映学习者在某一领域的知识水平的非空问题构成的集合称为问题域,通常记为Q={q1,q2,…,qn}.基于问题域,给出如下定义.

定义5[1]学习者在理想状态下能正确解决的问题域Q中的问题构成的集合,称为知识状态(Knowledge state),记为K.

所谓理想状态是指学生在没有受到外界压力或情绪影响的情况下,没有由粗心致错和侥幸蒙对的情况.

定义6[1]设K是问题域Q的一些子集构成的知识状态集族,且K至少包含∅和Q,则称（Q，K）为知识结构(Knowledge structure).

定义7[12]设（Q，K）为知识结构,若K 满足有限并封闭,即∀Ki,Kj∈K ⇒Ki⋃Kj∈K,则称（Q，K）为知识空间(Knowledge space)；若K 满足有限交封闭,即∀Li,Lj∈ ⇒Li⋂Lj∈K,则称（Q，K）为闭包空间（Closure Spaces）.

定义8[12]设G,G'分别为两个集族,若G'包含G中所有有限个元素的并组成的集合,则称集族G'是G的张成（span）,记为( G )=G',或G张成G'.

定义9[12]设（Q，K）为知识空间.若B 是张成K 的最小子集族,则称B 是（Q，K）的基（base）,且约定∅∉B.

李进金等[15]把知识空间的基称为知识基.若知识空间（Q，K）是有限的,则K 存在唯一的知识基.本文只讨论知识空间有限的情形.

定义10[13]三元组(Q,S,τ)称为一个技能映射,其中Q为问题域,S为非空技能集,τ是从Q到2S{∅}的映射.若s∉τ(q),则表示问题q的求解与技能s无关；若s∈τ(q),则表示问题q的求解与技能s相关.

技能映射主要通过析取模型与合取模型来诱导知识结构.技能子集T⊆S在析取模型下诱导的知识状态为K={q∈Q|τ(q)⋂T≠∅}.将T取遍S的所有子集,则所有知识状态构成的集族K 称为技能映射(Q,S,τ)在析取模型下诱导的知识空间.技能子集T⊆S在合取模型下诱导的知识状态为K={q∈Q|τ(q)⊆T}.将T取遍S的所有子集,则所有知识状态构成的集族L称为技能映射(Q,S,τ)在合取模型下诱导的闭包空间.若技能映射相同,则在析取模型下诱导的知识空间与在合取模型下诱导的闭包空间互为对偶.

定义11[13]设(Q,S,τ)为技能映射,若∀s∈S,技能映射(Q,S-{s},τS-{s})诱导的知识结构与(Q,S,τ)诱导的知识结构都不同,则称S为极小技能集,(Q,S,τ)为极小技能映射.

定义12[1]设(Q,K)是一个知识结构,≾为Q上的关系,记Kr={K∈K|r∈K}.若r≾q⇔r∈⋂Kq成立,则称≾为推测关系.当r≾q时,称由q可推测出r.

r≾q可直观理解为问题r比问题q更简单,学习者若能解决问题q,则必能解决问题r.

引理1[12]设(Q,K)是一个知识结构,记Kq={K∈K|q∈K}.对∀r,q∈Q,有r≾q⇔Kq⊆Kr.

引理2[1]设(Q,K)是一个知识结构.对∀r,q∈Q,r≾q⇔∀K∈K,有q∈K⇒r∈K.

2 技能映射与技能背景

问题与技能具有某些特定的关系.例如,学生想要解决某些问题,则必须掌握一些相关的技能.

定义13[11]三元组(Q,S,I)称为一个技能背景,其中Q为问题集,S为技能集.∀qj∈Q(j= 1,2,…,m)为一个问题,∀si∈S(i= 1,2,…,n)为一个技能.I是Q×S上的二元关系.若(q,s)∈I,则表示问题q的求解与技能s相关,用1表示.若(q,s)∉I,则表示问题q的求解与技能s无关,用0表示.

定义14设(Q,S,I)为技能背景,在问题集M⊆Q和技能集T⊆S上分别定义运算

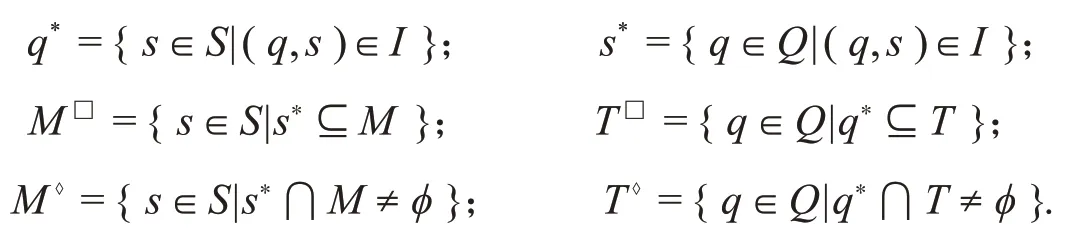
其中q*表示与问题q的求解相关的技能集；s*表示与技能s相关的问题集；M□表示只能与M中的问题求解相关的技能集；T□表示只能与T中的技能相关的问题集；M⋄表示与M中的问题求解相关的技能集；T⋄表示与T中的技能相关的问题集.

若M=T⋄,T=M□,则称(M,T)为面向问题概念；若M=T□,T=M⋄,则称(M,T)为面向技能概念.此时称M是面向问题（技能）概念的外延,T是面向问题（技能）概念的内涵.将面向问题概念格LO(Q,S,I)的所有外延构成的集族记为LOQ(Q,S,I),将面向技能概念格LP(Q,S,I)的所有外延构成的集族记为LPQ(Q,S,I).

对于技能映射(Q,S,τ),s∈τ(q)表示技能s与问题q的求解相关,故(q,s)∈I⇔s∈τ(q),即技能背景(Q,S,I)与技能映射(Q,S,τ)具有相互唯一确定的关系.

例1给定技能映射(Q1,S1,τ1),其中Q1={a,b,c,d,e},S1={s,t,u,v},τ1(a)={t},τ1(b)={t,v},τ1(c)={v},τ1(d)={s,u,v},τ1(e)={t,v}.

由(q,s)∈I1⇔s∈τ1(q)可得(Q1,S1,τ1)对应的技能背景(Q1,S1,I1)如表1所示.由文献[15]求面向对象（属性）概念格的方法,求得其对应的面向问题概念格LO(Q1,S1,I1)如图1 所示,面向技能概念格LP(Q1,S1,I1)如图2所示.

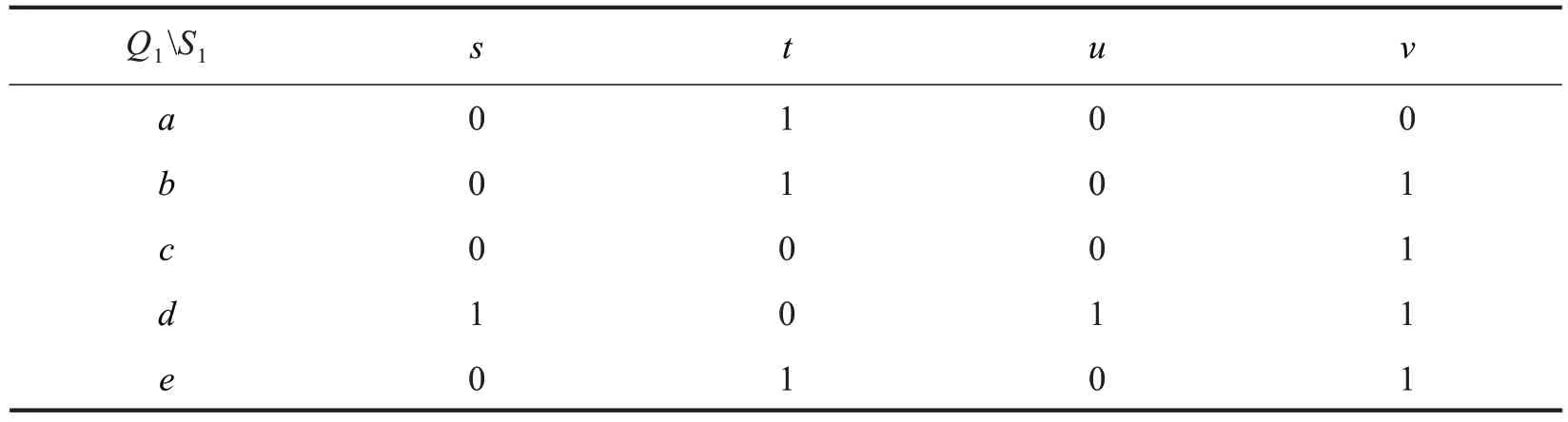
表1 技能背景(Q1,S1,I1)Tab.1 The skill context(Q1,S1,I1)

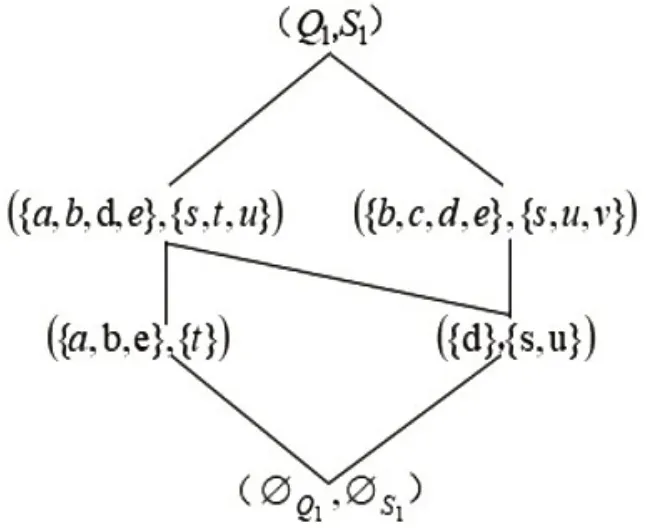
图1 LO(Q1,S1,I1)Fig.1 LO(Q1,S1,I1)

图2 LP(Q1,S1,I1)Fig.2 LP(Q1,S1,I1)

由图1,面向问题概念格LO(Q1,S1,I1)的外延有Q1,{a,b,d,e},{b,c,d,e},{a,b,e},{d},∅Q1,内涵有S1,{s,t,u},{s,u,v},{s,u},{t},∅S1.由图2,面向技能概念格LP(Q1,S1,I1)的外延有Q1,{a,b,c,e},{c,d},{a},{c},∅Q1,内涵有S1,{s,u,v},{t,v},{t},{v},∅S1.面向问题概念({a,b,d,e},{s,t,u})表示与{s,t,u}中的技能相关的问题是{a,b,d,e}.面向技能概念({a,b,c,e},{t,v})表示只能与{t,v}中的技能相关的问题是{a,b,c,e}.

3 技能背景与知识结构

给定技能映射可求出唯一的技能背景,再通过求解技能背景的面向问题概念格与面向技能概念格可迅速获得技能映射诱导的知识结构.由于部分技能子集诱导的知识状态可以被其他一些技能子集诱导的知识状态所取代,即S中的一些技能是冗余的,故有必要讨论技能约简的问题.

3.1 由面向问题（技能）概念格构建知识结构

由面向问题（技能）概念格的内涵与外延的关系,可得如下结论.

定理1设(Q,S,I)为技能背景,LO(Q,S,I)为其面向问题概念格,LP(Q,S,I)为其面向技能概念格.若(M,T)∈LO(Q,S,I),则内涵T在析取模型下诱导的知识状态为外延M.若(M,T)∈LP(Q,S,I),则内涵T在合取模型下诱导的知识状态为外延M.

证明对于面向问题概念(M,T),外延M表示与内涵T中的技能相关的问题集,则∀q∈M,都∃s∈T,使得(q,s)∈I,即s∈τ(q).于是∀q∈M,都有τ(q)⋂T≠∅成立,故面向问题概念的外延M为其内涵T在析取模型下诱导的知识状态.

对于面向技能概念(M,T),外延M表示只能与内涵T中技能相关的问题集,则∀q∈M,s∈S,若s∈τ(q),则必有s∈T成立,即∀q∈M,有τ(q)⊆T,故面向技能外延M为其内涵T在合取模型下诱导的知识状态.

定理2设(Q,S,I)为技能背景,LO(Q,S,I)为其面向问题概念格,LP(Q,S,I)为其面向技能概念格.若K是其所有面向问题概念的外延构成的集族,即K =LOQ(Q,S,I),则K 为知识空间.若L 是其所有面向技能概念的外延构成的集族,即L =LPQ(Q,S,I),则L 为闭包空间,且K 与L 互为对偶结构,即K={QK|K∈L}.

证明技能背景中面向问题概念格的所有外延构成的集族LOQ(Q,S,I)满足并封闭,面向技能概念格的所有外延构成的集族LPQ(Q,S,I)满足交封闭.又由定理1,可得K =LOQ(Q,S,I)为技能映射(Q,S,τ)在析取模型下诱导的知识空间,L=LPQ(Q,S,I)为技能映射(Q,S,τ)在合取模型下诱导的闭包空间,故K={QK|K∈L}.

例2对例1 的技能映射(Q1,S1,τ1),由定理2,其在析取模型下诱导的知识空间为K1={∅,{d},{a,b,e},{b,c,d,e},{a,b,d,e},Q1},在合取模型下诱导的闭包空间为L1={∅,{a},{c},{c,d},{a,b,c,e},Q1}.显然K1={Q1K1|K1∈L1}.

特别地,若技能子集T⊆S为单点集,即∀s∈S,T={s},则技能子集{s}在析取模型下诱导的知识状态为与技能s相关的问题集,在合取模型下诱导的知识状态为只与技能s相关的问题集.故可得如下结论.

推论1若(Q,S,τ)为技能映射,s∈S.则技能子集{s} 在析取模型下诱导的知识状态为K=s⋄,在合取模型下诱导的知识状态为K=s□.

由推论1,例1中的技能单点集{u}和{s} 在析取模型下诱导的知识状态均为{d} ,即知识状态{d}可由不同的技能子集诱导得到,从而有必要讨论技能的约简问题.

3.2 基于面向问题概念格的技能约简与知识基

同一技能映射下,若确定了其在析取模型下诱导的知识空间,则求其对偶结构可得其在合取模型下诱导的闭包空间.在知识空间理论中,技能约简是指保持知识结构不变,寻找极小技能集.本节基于面向问题概念格的技能约简,讨论保持知识空间不变的技能约简问题,并直接获得知识基.

技能映射(Q,S,τ)在析取模型下诱导的知识空间（Q，K）是其对应的技能背景(Q,S,I)确定的面向问题概念格的所有外延构成的集族,即K=LOQ(Q,S,I),故保持知识空间不变的技能约简可看成是面向问题概念格LO(Q,S,I)保持外延不变的技能约简,并将约简后得到的技能集称为技能约简集. 而LOQ(Q,S,I)={T⋄|T⋄□=T,T⊆ }S,且于是{x⋄|x∈S}可视为LOQ(Q,S,I)的并式生成组,即{x⋄|x∈S}可视为张成知识空间的集族.故面向问题概念格LO(U,A,I)保持外延不变的技能约简,可看成是LOQ(Q,S,I)的并式生成组的约简,即LOQ(Q,S,I)的最小并式生成组.综上可得如下结论.

定理3若X是技能背景(Q,S,I)确定的面向问题概念格LO(Q,S,I)的技能约简集,则LOQ(Q,S,I)的最小并式生成组B ={x⋄|∀x∈X}是技能背景(Q,S,I)对应的技能映射在析取模型下诱导的知识基.

推论2若X是技能背景(Q,S,I)确定的面向问题概念格LO(Q,S,I)的技能约简集,(Q,X,IX)是(Q,S,I)约简后的技能背景,则X为极小技能集,(Q,X,τX)为其对应的极小技能映射.

下面给出求解LOQ(Q,S,I)的最小并式生成组的方法,首先给出如下定义.

定义15设技能背景(Q,S,I)确定的面向问题概念格为LO(Q,S,I),x∈S.若∃T⊆S,x∉T,使得x⋄=则称x⋄为技能并式可约元（简称并式可约元）.

记关系R={(x,y)|x⋄=y⋄,x∈S,y∈S},则R是技能集S上的等价关系,于是得到技能集S的一个划分：S/R={[x]R|x∈S},其中[x]R={y|(x,y)∈R,y∈S}.

求解LOQ(Q,S,I)的最小并式生成组的步骤为：

1）对每个x∈S,求出外延x⋄；

2）求S/R={[xi1],[xi2],[xi3],…,[xik]}；

3）从等价类[xit] 中各抽取一个元素xi作代表元(1 ≤t≤k,1 ≤i≤ ||S),组成技能集Dj={xi|1 ≤i≤ ||S},(1 ≤j≤ ||S)；

4）若∀xi∈Dj,∃xi′∈Dj使得则将xi从Dj中删除,得到LO(Q,S,I)的一个技能约简集,取遍j得到全部的技能约简集.

步骤4)由{xi⋄|xi∈Dj}通过并运算生成{T⋄|T⊆Dj},从而把所有的并式可约元找出来并删除,则可求得LOQ(Q,S,I)的最小并式生成组.

由于技能等价类的存在,所以技能约简集可能不唯一,故极小技能集和极小技能映射可能不唯一.

推论3设(Q,S,I)为技能背景,x∈S.若技能等价类[x]R均为单点集,则极小技能集和极小技能映射唯一.

由于极小技能映射(Q,X,τX)和技能映射(Q,S,τ)通过析取模型诱导的知识空间相同,且∀x∈X,x⋄是技能子集{x} 在析取模型下诱导的一个知识状态,故可得如下推论.

推论4若X⊆S为极小技能集,则极小技能映射(Q,X,τX)和技能映射(Q,S,τ)在析取模型下诱导的知识基相同,且都为B ={x⋄|∀x∈X}.

例3给定技能映射(Q2,S2,τ2),其中Q2={a,b,c,d,e},S2={s,t,u,v,w},τ2(a)={s,t,v},τ2(b)={s,t,u},τ2(c)={t, }u,τ2(d)={s,t,w},τ2(e)={w}.其对应的技能背景为(Q2,S2,I2)如表2所示.

表2 技能背景(Q2,S2,τ2)Tab.2 The skill context(Q2,S2,τ2)

则有：

1）s⋄={a,b,d},t⋄={a,b,c,d},u⋄={b,c},v⋄={a},w⋄={d,e}；

2）S/R={[x1],[x2],[x3],[x4],[x5]},其中[x1]={s},[x2]={t},[x3]={u},[x4]={v},[x5]={w},即每个技能等价类均为单点集；

3）得到一个技能集D1={s,t,u,v,w}；

4）由于t⋄={a,b,c,d}=s⋄⋃u⋄,故删除t,得到LO(Q,S,I)的技能约简集为X2={s,u,v,w}.

于是技能背景(Q2,S2,I2) 确定的LOQ(Q2,S2,I2) 的并式最小生成组为{s⋄,u⋄,v⋄,w⋄}, 即{{a,b,d},{b,c},{a},{d,e}},故技能映射(Q2,S2,τ2)通过析取模型诱导的知识基为B ={{a},{b,c},{d,e},{a,b,d}}.由推论3,此时极小技能集X2={s,u,v,w}与极小技能映射(Q2,X2,τX2)唯一,其中τX2(a)={s,v},τX2(b)={s,u},τX2(c)={u},τX2(d)={s,w},τX2(e)={w}.

对例1的技能映射(Q1,S1,τ1),有

1）s⋄={d},t⋄={a,b,e},u⋄={d},v⋄={b,c,d,e}；

2）S/R={[x1],[x2],[x3]},其中[x1]={s,u},[x2]={t},[x3]={v},显然技能等价类[x1]不为单点集.由推论3,此时极小技能集与极小技能映射不唯一.

4 基于技能背景的推测关系

问题的推测关系反映了问题之间的难易性与顺序性,是后期建立学习者的学习路径的一个重要参考.但由析取模型与合取模型取遍S的所有技能子集去诱导知识结构,再计算推测关系,计算量较大,过程过于繁杂.本节基于技能背景,可直接得出问题之间的推测关系,不必求出技能映射诱导的知识结构,省去了复杂的计算过程.

定理4设(Q,S,I)是技能映射(Q,S,τ)对应的技能背景,

1）若（Q，K）是知识空间,则∀r,q∈Q,有r≾q⇔q⋄⊆r⋄；

2）若（Q，K）是闭包空间,则∀r,q∈Q,有r≾q⇔r⋄⊆q⋄.

证明1）设技能子集T在析取模型下诱导的知识状态是K,q⋄表示与问题q的求解相关的技能,则q⋄⋂T≠∅⇔τ(q)⋂T≠∅.若r≾q,由引理2可得,对∀K∈K,都有q∈K⇒r∈K,即q⋄⋂T≠∅⇒r⋄⋂T≠∅,故q⋄⊆r⋄.若q⋄⊆r⋄,对∀q∈K,有q⋄⋂T≠∅,又因为q⋄⊆r⋄,则r⋄⋂T≠∅,即r∈K.又由引理2,可得r≾q.

同理可证2）.

例4对例1的知识空间（Q1，K1）,显然有a⋄⊆b⋄,于是b≾a.同理有e≾a,e≾b,b≾c,d≾c,e≾c,b≾e.

定理5设(Q,S,I) 是技能映射(Q,S,τ) 对应的技能背景. 若（Q，K）是知识空间,记Fq={x⋄|q∈x⋄,x∈S},则∀r,q∈Q,有r≾q⇔Fq⊆Fr⇔r∈⋂Fq.

证明1)若Kq⊆Kr,因为x⋄是单点集{x} 在析取模型下诱导的知识状态,故Fq⊆Fr.若Fq⊆Fr,记F={x⋄|x∈S},对于∀Kq⊆Kr,有K1=x⋄⋃y⋄,其中x⋄∈Fq,y⋄∈F.由于Fq⊆Fr,则∃x′⋄∈Fr,使得x′⋄=x⋄,K1=x⋄⋃y⋄=x′⋄⋃y⋄=K2∈Kr成立,故Kq⊆Kr.又由引理1,有r≾q⇔Kq⊆Kr,故r≾q⇔Fq⊆Fr.

2)由定义12与引理1,有r≾q⇔Kq⊆Kr⇔r∈⋂Kq,又因为r≾q⇔Fq⊆Fr,故r≾q⇔r∈⋂Fq.

综上,可得r≾q⇔Fq⊆Fr⇔r∈⋂Fq.

推论5设(Q,S,I)是技能映射(Q,S,τ)对应的技能背景.若（Q，K）是知识空间,X是技能约简集,记Fq′={x⋄|q∈x⋄,x∈X},则∀r,q∈Q,有r≾q⇔Fq′⊆Fr′⇔r∈⋂Fq′.

例5对例2 的技能映射(Q2,S2,τ2)诱导的知识空间,有Fa={s⋄,t⋄,v⋄},Fb={s⋄,t⋄,u⋄},Fc={t⋄,u⋄},Fd={s⋄,t⋄,w⋄},Fe={w⋄},则Fc⊆Fb, Fe⊆Fd,故b≾c,d≾e.由例2 可得技能约简集X2={s,u,v,w},于是Fa′={s⋄,v⋄},Fb′={s⋄,u⋄},Fc′={u⋄},Fd′={s⋄,w⋄},Fe′={w⋄},则Fc′⊆Fb′,Fe′⊆Fd′,故b≾c,d≾e.所得结果与未知技能约简集结果一致.

显然由r≾q⇔r∈⋂Fq,其中Fq={x⋄|q∈x⋄,x∈S},可得若q∈x⋄,则r∈x⋄,故可得如下推论.

推论6设(Q,S,I) 是技能映射(Q,S,τ) 对应的技能背景,（Q，K）是知识空间. 对∀r,q∈Q,r≾q⇔∀x∈S,都有q∈x⋄⇒r∈x⋄.

由于r≾q⇔Kq⊆Kr,且技能映射在析取模型（合取模型）下诱导的知识结构可由其对应的面向问题（技能）概念格的外延集来确定,故基于面向问题（技能）概念格的外延与内涵的关系,可给出Kq⊆Kr的一个等价条件.

定理6设(Q,S,I)是技能映射(Q,S,τ)对应的技能背景,

1）若ℳq为技能背景(Q,S,I)所确定的面向问题概念格LO(Q,S,I)中所有包含问题q的外延构成的集族,即ℳq={M∈LOQ(Q,S,I)|q∈M},且ℳq□={M□|M∈ℳq}.则∀r,q∈Q,有r≾q⇔ℳq□⊆ℳr□；

2）若ℳq′为技能背景(Q,S,I)所确定的面向技能概念格LP(Q,S,I)中所有包含问题q的外延构成的集族,即ℳq′={M′∈LPQ(Q,S,I)|q∈M′},且ℳq′⋄={M′⋄|M′∈ℳq′}.则∀r,q∈Q,有r≾q⇔ℳq′⋄⊆ℳr′⋄.

证明1）若Kq⊆Kr,即ℳq⊆ℳr,因为M□={s∈S|s∗⊆M},则ℳq□⊆ℳr□.另一方面,若ℳq□⊆ℳr□,因为M□⋄={q∈Q|q∗⋂M□≠ϕ},故ℳq□⋄={M□⋄|M∈ℳq}⊆ℳr□⋄={M□⋄|M∈ℳr},又因为在LO(Q,S,I)中有M□⋄=M,故ℳq□⋄={M|M∈ℳq}⊆ℳr□⋄={M|M∈ℳr},即ℳq⊆ℳr,即Kq⊆Kr. 综上,可得Kq⊆Kr⇔ℳq□⊆ℳr□.又由引理1,有r≾q⇔Kq⊆Kr,故r≾q⇔ℳq□⊆ℳr□.

同理可证2）.

5 结束语

本文将知识空间理论与形式概念分析中的面向对象（属性）概念格相联系.基于面向问题（技能）概念格,快速确定技能映射诱导的知识结构.此外,对知识基、技能约简以及推测关系与面向问题（技能）概念格的关系进行了研究.本文主要运用形式概念分析讨论了知识空间和闭包空间,今后将进一步研究知识空间理论中的其他知识结构与形式概念分析的联系.