利用数形结合，培养高中数学解题能力

南京市六合区程桥高级中学 翁兴超

目前，数形结合思想被广泛应用到了高中数学的学习之中，可以有效提高学生的解题效率与质量，能够保证学生掌握多种数学知识，推动学生全面发展。数形结合最主要的特点就是形象、简单、直观，高中数学教师要培养学生的数学解题能力，就一定要充分发挥数形结合的优势，把抽象的数学内容具体化。

一、转化图形与代数问题

在高中数学教学之中，有些传统的解题方式会浪费学生的时间，教师可以教给学生利用图形把代数题目转化成图形题目，筛选、删除题目中的干扰条件，利用图形发现题目的本质，然后再结合数学公式去解答题目，使用数形结合的思想能够更好地培养学生的解题能力。

例1：已知关于x的方程x2-4|x|+5=m有4个不相等的实根，求m的取值范围。

解：根据方程式能够联想，把其和函数结合在一起，令y1=x2-4|x|+5，y2=m，然后画出函数图像，如图1。从图1中能够清晰地看到若要满足方程式有四个不相等的实根时，1＜m＜5。学生利用图像能够更加直观地解答复杂的数学问题，而且更加简单、快捷。

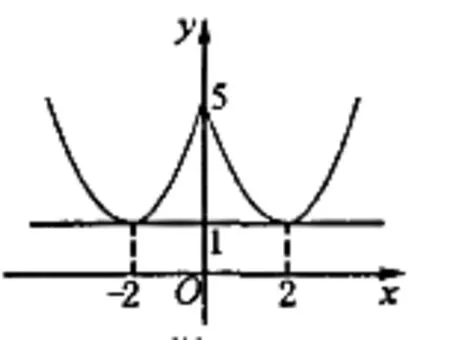
图1

二、发散思维，产生图形意识

高中时期的学生依然对生活充满了兴趣与好奇，教师应该根据学生的特点，引导学生发现问题、探索问题。高中生应该养成主动探究学习与生活的习惯，数学教师在教学中也应该培养学生发现问题的能力，这对于学生的学习有着非常积极的作用。学生在学习时会遇到很多困难，有些学生会因为不理解数学理论知识而产生问题，有些学生会因为遇到一些没有学过的知识而产生问题等。高中数学教师应该提升学生发现问题的意识，引导学生利用发散思维去探究解决问题，并提供一些案例让学生自主研究，使之产生图形意识，提高探究式的学习能力。同时，高中数学教师也要引导学生使用数形结合的思想，逐渐增加学生的解题兴趣，让学生可以扩展思维，主动学习其他方面的数学知识，以此提高学生的数学解题能力和思维能力。

例2：已知0＜a＜1，求方程a|x|=|logax|有几个实数根。

解：将方程联系函数，令y1=a|x|，y2=|logax|，作出两函数图像，如图2所示，因为此图像中有两个交点，所以方程中有两个实数根。

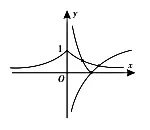
图2

三、在作业中渗透

高中数学教师应该改变之前传统的教学方式，适当地给学生布置一些数形结合的作业，教给学生利用数形结合去解决问题的方法。数学教师应该结合在课堂上所教授的数学知识，给学生布置一些具有针对性的、可以利用数形结合思想解决的练习题，通过让学生进行大量的练习，能够让学生对数形结合思想记忆深刻，并养成利用数形结合解题的习惯。特别是在做选择题的时候，倘若高中生可以利用数形结合，那么不用进行复杂的运算，而是直接画出图形就可以迅速得到答案。总之，利用数形结合能够有效培养高中生的数学解题能力，让学生在考试中节省很多时间，也可以增加答案的准确度。

例3：已知P是圆（x-3）2+(y+1)2=4上面的动点，Q是直线x=-3上面的动点，求|PQ|的最小值。

解：根据题目画出图3所示的图形。过圆心A作直线x=-3的垂线，与圆和直线分别交于P、Q，这时|PQ|取最小值，与题目中圆的方程相结合能够得到A（3，-1），半径r=2，因此|PQ|=|AQ|-r=6-2=4，所以|PQ|的最小值是4。

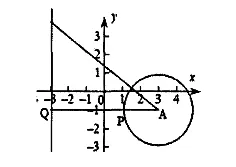
图3

综上所述，在高中数学教学之中，为了满足新课改的需要，教师应该想方设法地提高学生的解题能力，而数形结合正是一种较为有效的解题方法，可以使学生的思维严密、全面思考问题、减少解题中的漏洞等。数形结合对于高中生的学习来说有着很大的帮助，对于解答集合问题、函数问题、几何问题、排列组合问题等都有着十分重要的作用，而且对教师的教学也有十分重要的意义，可以有效提高学生的数学解题能力，同时提升课堂教学效率。