初中数学发散性思维能力培养策略研究

安徽省无为第二中学 郑天明

随着素质教育的不断深入和推广，教师的教学方式和教育理念产生了巨大的变化，从致力于引导学生熟练掌握解题方法转化为帮助学生形成正确的数学思维，“授人以鱼不如授人以渔”，从学生长远发展的角度来看，培养学生的发散性思维比教育学生解决有限的数学问题更加重要。

一、发散性思维

与其他思维能力相比，发散性思维的显著特征表现如下：第一，流畅性。发散性思维需在较短时间内产生多种思维观念并快速适应新思想，流畅性主要反映的是发散思维能力的数量和速度等特征。第二，变通性。发散性思维需要摆脱脑海中现有的思维框架，开拓新的思维方向来思索和探究问题，如横向类比、触类旁通、跨域转化等等，通过将思维向不同方向进行扩散来获取多种解题思路。第三，独特性。发散性思维会使人们采用不同于常规的问题解决方式，因而具备一定的独特性。

二、具体培养策略

1.一题多变

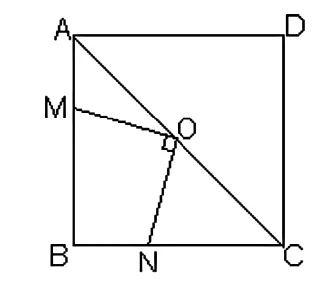
图1

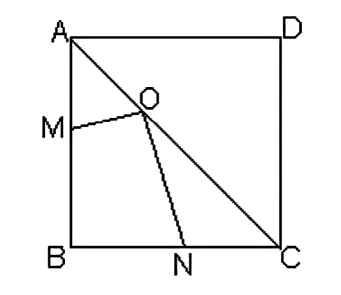
图2

图3

2.一题多解

一题多解是发散性思维中变通性特征的体现，数学教师在针对教材内容中一些具有代表性意义的数学题目进行讲解时，需要引导学生充分运用所学知识进行发散性思维，从多个角度来论证同一论点，通过这种方式来培养学生发散性思维中的变通性。例如：“如图4所示，在△ABC中，AB=AC，D是BC上一点，DE⊥AB于点E，DF⊥AC于点F，BG是AC边上的高，求证：DE+DF=BG。”针对这一几何问题，教师就可以先让学生分析题目中的已知条件，之后再向学生提出问题：该数学题目属于哪类几何证明题？应用哪种几何证明方法进行证明？如何添加辅助线？需要用到什么数学知识点？在提出问题之后，教师可组织学生针对该数学题目进行小组讨论，一一解答上述问题，即该问题属于几何证明题中的线段和差问题，应用截长补短法进行证明，过D点作BG的垂线DH，利用全等三角形和矩形等知识点来逐步完成证明。

图4

当学生按照常规解题思路完成对该数学题目的解答后，教师可以启发学生探究该题目的其他证明方法，如：辅助线还有其他作法吗？启发学生通过其他方式来解决数学问题，过B点作FD的垂线与延长线交于点K，沿用全等三角形和矩形的知识点可完成证明。再例如，教师可向学生提问：DE、DF、BG是△ABD、△ACD、△ABC的什么？当学生回答是三角形的高时，再进一步向学生提问：三角形的高与三角形的什么有关？学生答“面积”。教师继续向学生提问：这道几何证明题可以用面积法论证吗？通过引导启发的方式，让学生从割补思想的角度利用面积法来证明。除此之外，教师还可以继续让学生发散思维：△BDE、△CDF和△BCG都属于什么类型的三角形呢？学生回答“直角三角形”。教师继续提问：∠ACB和∠ABC之间存在什么数量关系呢？学生回答“∠ACB＝∠ABC”。教师提问：直角三角形的角和边存在怎样的关系？学生回答“三角函数关系”，接着教师可引导学生利用三角函数的知识点来证明该数学题目。

在整个解题的过程中，教师循序渐进地引导学生合理运用多种思维方式来解决同一数学问题，寻求一题多解，开拓学生的解题思路，从而有效地培养了学生的发散性思维。

3.创新解法

创新解法是发散性思维中独特性特征的体现，在初中数学题目中，不乏一些条件隐蔽且构思巧妙的题目，针对这些题目，教师可在学生能够熟练掌握常规解题思路的基础上，带领其积极探寻一些非常规的解题方法，如构造法、数形结合法、代换法等等，通过对创新解法的探究，可以有效地提高学生的发散性思维能力。例如：“若y=|x+2|+|x+1|+|x-1|+|x+2|，求当x取何值时，y恰好为最小值？最小值为多少？”教师首先带领学生对该数学问题进行分析：这道题目想要考查的是哪个数学知识点？学生首先想到的是该题目考查的是绝对值的知识点，常规的解题思路为根据绝对值的定义对不同区间进行分类讨论，得出一个分段函数，在此基础上求取最小值。这种常规的解题思路虽然可以解决该数学问题，但相对来说过程较为复杂，因此，教师可引导学生思考是否有其他非常规的解题思路，若学生未能想到创新解法，则教师可以试探性地引导学生思考绝对值的几何定义，并对该定义进行适当推广，|x|的几何定义为x在数轴上的对应点与原点O的距离，将|x|换一种表达方式，即|x-0|，其中0所对应的则是坐标轴中的原点O，在此基础上进一步推广|x-m|，其几何意义则可以理解为x与m在数轴上的距离，由此可得，y可以表示为x在数轴上分别与-2、-1、1、2之间的距离之和，因为x可以为数轴上的任意一点，因此我们可以判断出当-1≤x≤1时，y值最小，且最小值为6。

对于一道简单的数学题目而言，创新解题方法，积极引导学生从非常规的角度来分析和解决数学问题是培养学生发散性思维的重要方式，这样不仅可以让学生学会从新角度去解决问题，用新观念去看待问题，锻炼学生的思维灵活性，同时还可以帮助学生树立正确的数学思维，有利于克服思维定式对学生数学思维的束缚和限制，强化教学效果。