解析几何中的定点定值问题的策略与方法

广东省深圳市南头中学 武文香

解析几何的解题过程中，需要学生全面地看待问题，寻找题目中条件之间的联系，并使用发展的观点来处理这类问题。解析几何中的定值、定点等问题对学生而言是难点，加上高考对此类题目的重视程度越来越高，因此，教师对此展开教学研究是非常必要的，能够帮助学生提升数学逻辑思维，锻炼数学能力，使其在高考中获得更高的分数。

一、定点解析几何

定点的解析几何主要是从椭圆或是圆的性质出发，进一步要求学生掌握图形与直线的位置关系、平面向量关系等，其中对学生的运算能力有较高的要求，对学生的推理论证能力有一定的考查，涉及的解题思路主要是数形结合、转化归化以及函数方程三个方面。

例1：平面直角坐标系xOy中，二次函数f（x）=x2+2x+b（x∈R）与x轴和y轴有三个交点，经过三个交点的圆为C。（1）求实数b的取值范围；（2）求圆C的方程；（3）圆C是否经过定点（该点的坐标与b无关）？证明此结论。

解析此题时，我们将（1）和（2）问忽略，仔细求解（3）问。这题有两种解题方法——

一般法：从（2）中能够知道圆C方程为：x2+y2+2x-（b+1）y+b=0，此时令b=0，则x2+y2+2x-y=0，令b=-1，则x2+y2+2x-1=0，联立求解得x=0，y=1或x=-2，y=1。因此，圆C必过定点A（0，1）和B（-2，1）。证明过程如下：将点A（0，1）代入方程之中，则左边=02+12+2×0-（b+1）+b=0，右边=0，所以圆C过定点（0，1）。同理可证，圆C也会过定点（-2，1）。

形象法：基于圆C必过定点，证明：假设圆C过定点（x0，y0），此时的x0和y0均不依赖于b，将其代入圆C方程中，则++2x0-y0+（1-y0）b=0（即为方程D），方程中所有满足b＜1（b≠0）都必须要成立，则1-y0=0必须成立。根据方程D得到++2x0-y0=0，解得x0=0，y0=1或x0=-2，y0=1。根据经验可知，点（0，1）和（-2，1）都在圆C上，所以圆C经过定点。

在解析这类题目时，教师首先要教会学生求解出动曲线的方程，再进一步求定点。方法可选择一般法或是形象法，一般法可通过取特殊值来确定定点，进一步加以证明；形象法则是根据参数无关的性质，从含有参数的动圆的方程必然成立的角度来证明其必然成立，再根据系数的关系来确定定点。对于这两种方法，教师可根据学生的理解程度进行教学，这样才符合因材施教的教学理念。至于具体的教学方法，教师应该根据学生的情况进行必要的强化训练，使学生能够掌握这类题目的知识点和难点，再从得分的角度给予解题思路、得分要点、易错点的引导，最终使学生能够将这类题目解答出来。

二、定值解析几何

全国卷或是各地命题的高考试卷、高考模拟卷中运用解析几何解答实际问题，近年来都表现出对称性和对等性的问题，运算过程中，这些线索和答案具有一定的对偶性。如果能够从美学观点出发，再辅助学生更多的解题策略，整个运算过程和解题过程就更加自然流畅。教学活动中，设而不求、构建坐标是常见的解题思路。

1.设而不求

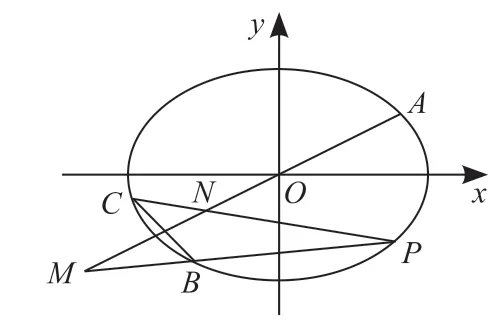
图1

解题时，从运算能力、数形结合、函数方程等思维入手教学，建立等量关系时从P、M、N三点的坐标出发，体现设而不求的思想。

2.坐标求解

例3：如图2所示，圆O：x2+y2=r2（r＞0），M、P是圆O上任意两点。圆O上的N点与M点关于x轴对称，直线MP和NP分别与x轴交于A点和B点，求证：A、B两点横坐标之积是定值。

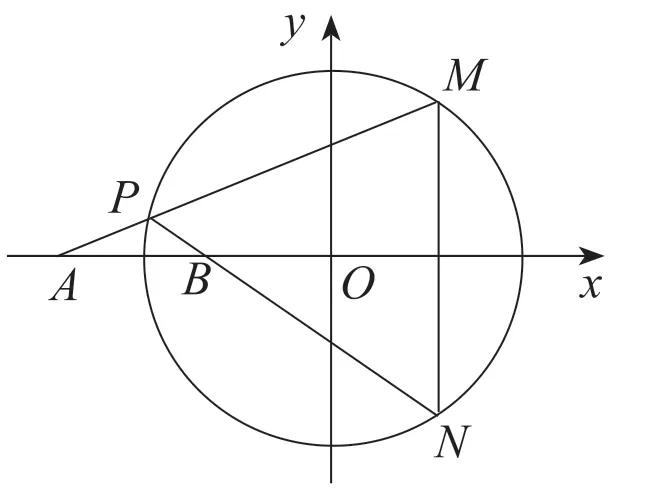
图2

解决这类定值问题首先应假设出动点的坐标，将其作为参数代入条件中，求出相关的变量，建立联系，再将椭圆上的点的坐标代入满足椭圆方程，消除参数，最终可获证。

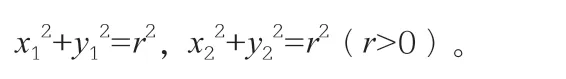
解析几何需要学生从整体上把握题目所给的信息，并将其转化为解题的线索，恰当地利用方程思想、函数思想、转化归化思想和数形结合思想进行分类讨论，进而得到答案。总的来说，定点是直线过定点或是曲线过定点，定点的坐标就是定值，定值问题则是证明某式为定值。实践中需要多总结、反思，积累经验，提高解题能力。