顾及传播曲面的多波束波束脚印高精度快速归位算法
2021-06-25毕自军赵建虎刘美琴
毕自军,赵建虎,郑 根,刘美琴
1. 武汉大学测绘学院,湖北 武汉 430079; 2. 武汉大学海洋研究院,湖北 武汉 430079
海底地形是海洋基础地理信息的重要组成部分,多波束测深系统是高效获取海底地形的典型设备之一[1-3],位置归算是获取高精度多波束测深点的重要环节[4-5],为此,国内外学者进行了大量研究。文献[6]提出了多波束精密声线跟踪算法和测深点归位计算模型,并指出姿态角对归位计算精度影响显著;文献[7]分析了姿态误差对归位计算的影响,并利用傅里叶变换对其进行去除;文献[7—8]推导了顾及姿态的声线跟踪模型,并在浅水区验证了其有效性;文献[8—9]通过坐标旋转建立了顾及船姿的波束入射向量计算模型,提高了声线跟踪和归位计算精度。以上研究都假设波束发射和接收过程共路线或路线对称。文献[10—12]指出,受测量船运动和姿态瞬时变化的影响,上述假设与实际存在差异,这种影响在浅水区并不明显,但随着船速增大和水深增加,归位计算误差越来越大,严重影响多波束测深精度。
文献[11]提出虚拟同心阵(virtual concentric array,VCCA)模型,根据收/发传感器姿态和波束指向角建立收/发矢量锥面,且假设波束的传播路径为:从收/发时刻传感器位置的中点处发出并在海底散射后沿原路径返回。VCCA顾及收/发位置差异,一定程度上改善中深水的波束脚印归位计算精度,但其所假设的波束传播路径降低了归算精度。文献[12]在VCCA模型基础上建立了非同心阵(non concentric array,NCCA)模型,即在平行于收/发阵的平面族内以非同心双曲线交点估计波束脚印,根据声线跟踪的双程时间与观测时间,迭代调整目标平面与换能器间距离,完成波束脚印位置归算。NCCA顾及了波束收/发阵列位置的不同,改善VCCA的理论精度,但仍存在多次迭代导致的效率较低等问题。文献[13]对VCCA模型进行了推导和简化,提高了计算效率,但计算精度与VCCA模型近似。
为此,本文基于多波束测量原理和波束传播理论,建立波束传播曲面模型,进而提出一种高精度高效率的波束脚印位置归算方法。
1 位置归算基本原理及传播曲面模型
文献[12]指出波束脚印为收/发波束在海底形成各自波束脚印的交集,归算步骤如下。
(1) 坐标参考系。为构建传播曲面模型,需定义相关坐标参考系。本文传感器阵列坐标系:以阵列中心为坐标原点,x轴指向船左舷方向,y轴指向航向,z轴与x、y轴构成右手正交坐标系;当地水平坐标系:以传感器中心为坐标原点,X轴指向地北子午线方向,Y轴指向东,Z轴与X轴、Y轴构成右手正交坐标系[14-15]。以下步骤(2)—步骤(3)基于当地水平坐标系,各矢量均需经传感器坐标系旋转至当地水平坐标系[11];步骤(4)中收/发传播曲面需转换至船中心为原点的水平坐标系或地理坐标系下。

(3) 根据声速剖面,建立收/发波束传播曲面。传播声线为各RV/TV对应的声波传播路径,可根据声速、声线方位角θ、俯角φ,借助声线跟踪获得(图1(b))。收/发矢量锥面上所有矢量对应的传播声线集合构成收/发传播曲面(图1(c))。下称传播曲面与等深面F的交线为截线,声线与等深面F的交点为截点。
(4) 确定实际波束脚印。各个等深面内可确定发射截线与接收截线交点(图1(d)),所有等深面内该交点的连线即为收/发传播曲面的交线,由双程传播时间可在该交线上确定波束脚印位置。
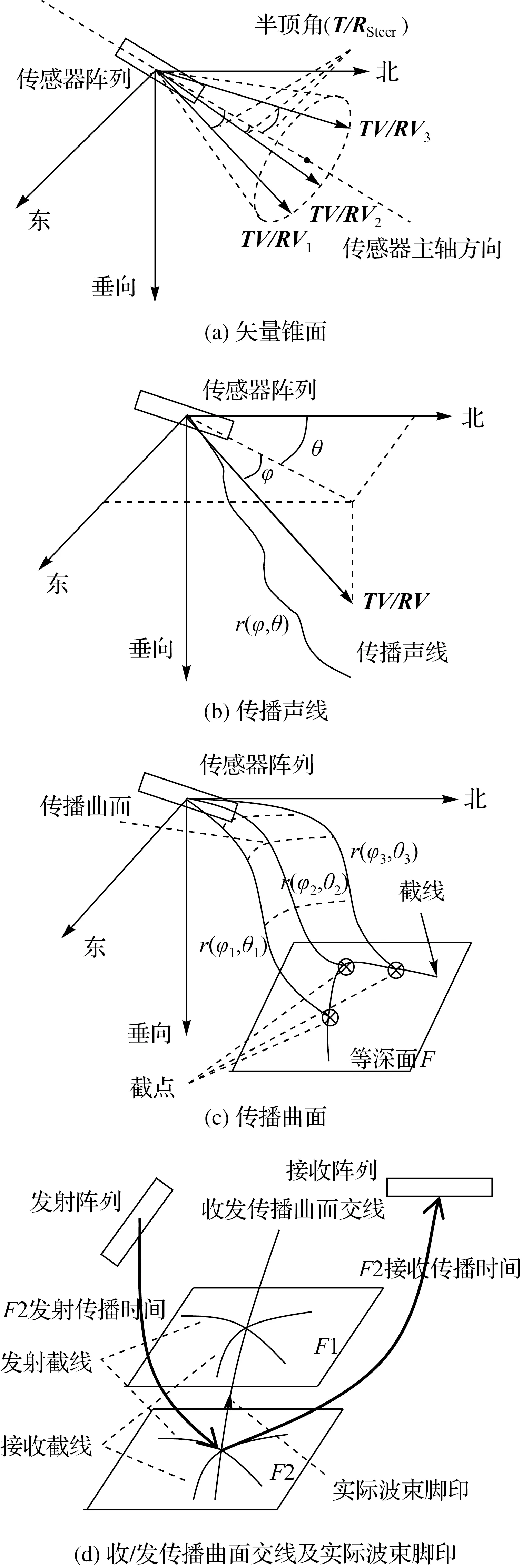
图1 波束脚印位置归算原理Fig.1 The principle of beam footprint position reduction
以上步骤中,传播曲面的建立是确定截线并最终获得波束脚印的关键。以发射为例,该过程在当地水平坐标系下可分为4步:①确定发射锥面主轴方向单位矢量(TX)和锥面半顶角;②计算遍历初始矢量(Tfirst);③遍历全部TV;④计算各TV对应θ、φ并根据声线跟踪形成声线,声线集合即为发射传播曲面。

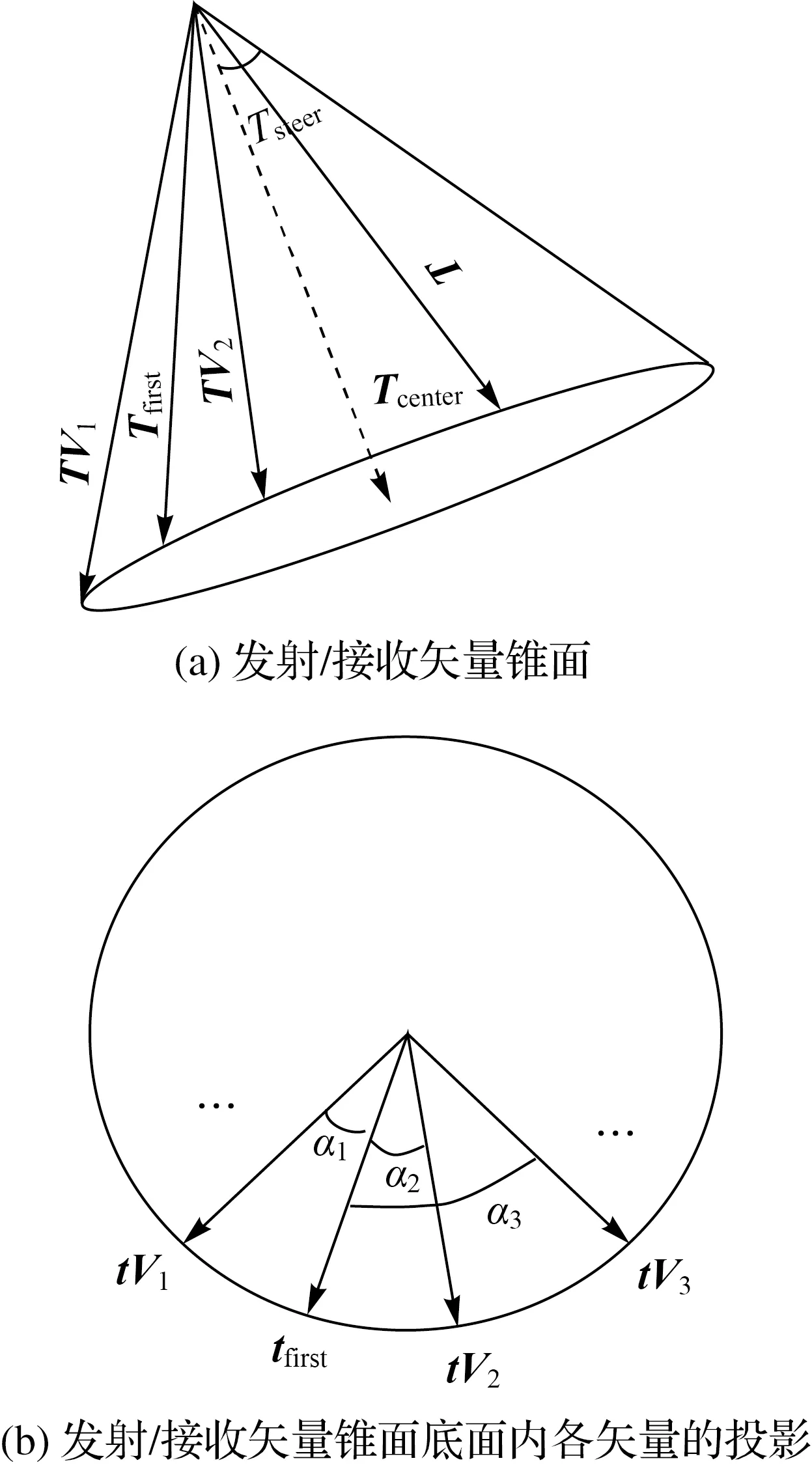
图2 遍历波束发射/接收矢量Fig.2 Traverse transmit/receive vector
则对于锥面上任意矢量TVi满足式(1)—
式(3)
(1)

(2)
|TVi|=1
(3)
根据式(1)—式(3),对每一个αi均可计算其对应矢量TVi为(XTVi,YTVi,ZTVi)。因此,通过在[-180°,180°]内遍历α即可计算锥面上每一个TV的矢量坐标,实现遍历。
矢量TVi对应的方位角θi和声线俯角φi由式(4)—式(5)计算
(4)
φi=90-arcsin(ZTVi)
(5)
基于θi和φi,根据常梯度声线跟踪[16-20],保留所有收/发声线路径,即可形成收/发传播曲面。在收/发传播曲面交线上找到收/发传播时间等于观测双程时间的点,即为波束脚印,图3描述了该过程。

图3 传播曲面模型Fig.3 The propagation surface model
2 顾及传播曲面模型的高效归算算法
传播曲面模型理论严密,但建立收/发传播曲面耗时较长,为此下面给出一种高效、高精度归算算法。
为提高计算效率,本文采用如下策略:将扇区内波束分为插值结点和待插值点;前者用迭代搜索,替代完整传播曲面的建立;后者用插值结点归算结果开展参数插值,避免多次迭代(图4)。
具体实施如下:
步骤1 在扇区内,等间隔选取5个波束作为插值结点,其他波束作为待插值点。
步骤2 插值结点位置计算。
(1) 利用VCCA模型计算起始矢量Tfirst、概略深度D0和概略声程L0。
(2) 由D0和平面精度ε0,计算等深面内,两个发射或接收截点间的直线距离(下称发射或接收截点间距)的上限MT、MR。
(3) 结合ε0、D0、L0设置迭代收/发遍历角度α的初始区间(αR1,αR2)、(αT1,αT2)和深度区间(D1,D2)。
(4) 分别对αR1、αR2对应的两个接收矢量和αT1、αT2对应的两个发射矢量声线跟踪,统计这4根声线在D1、D2两个等深面内的收发传播时间和tD1、tD2及D2等深面内收/发截点间距MR1-R2、MT1-T2。
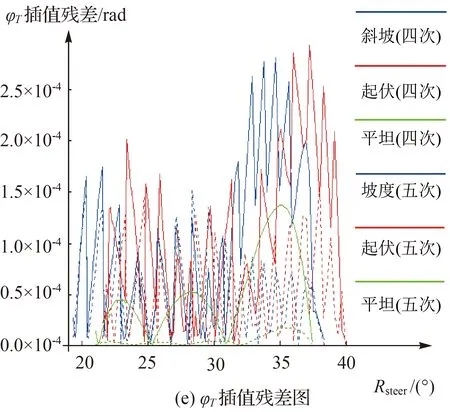
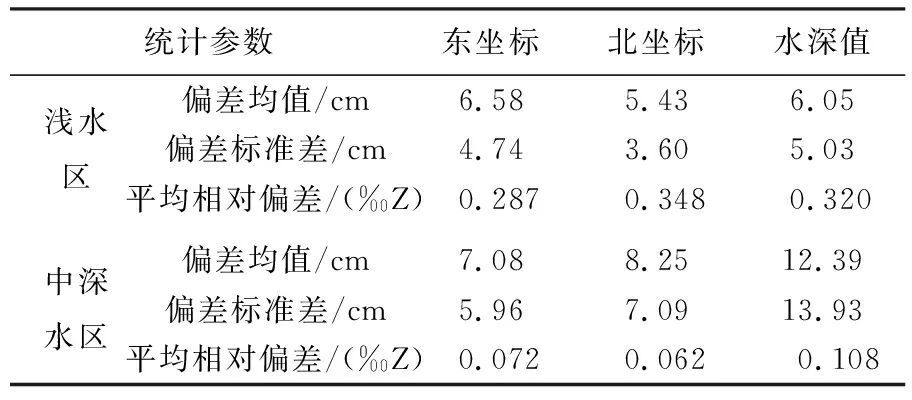
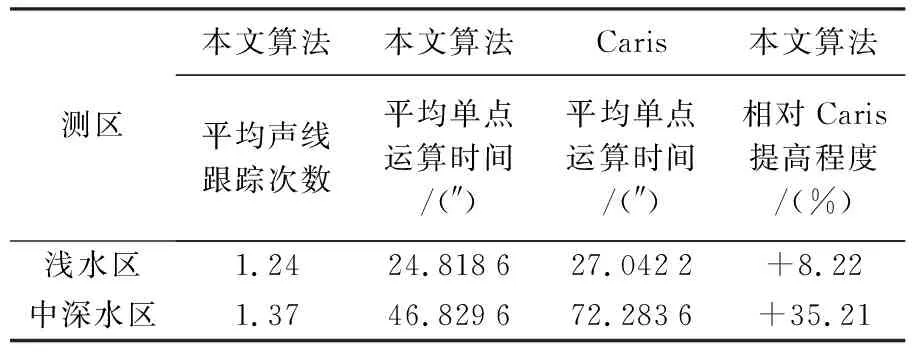
(5) 若MR1-R2 (6) 根据tD1、tD2、t0赋权,由D1、D2等深面内四组截点坐标插值得到波束脚印位置。 步骤3 待插值点位置计算。 (4) 由φTi、θTi声线跟踪至tTi耗尽,即为第i个待求波束脚印位置。 同理完成全部待插值点归算,即实现全扇区波束脚印位置归算。 2.1.1 截点间距上限MR、MT确定 不考虑截线的几何特性,当迭代终止条件设为MR1-R2<ε0、MT1-T2<ε0时,可得到严密结果。但为了减少迭代次数,上述算法结合截线的最小曲率半径,计算满足ε0时的截点间距上限MR、MT,将迭代终止条件设为MR1-R2 若不考虑折射,收/发传播曲面是由收/发矢量锥面延伸形成的圆锥面,任意等深面内的收/发截线均为圆锥曲线[22]。如图5所示,A点为实际收/发截线的交点,B点为收/发截点连线的交点;εR、εT表示收/发截线以直代曲的偏差,当εR、εT的最大值均小于0.5ε0时,以B点代替A点的偏差小于ε0。εR、εT最大值为:半径为截线最小曲率半径,弦长等于MR、MT的圆弧的拱高。推导可得MR/MT满足式(6),式中ρR和ρT表示收/发截线最小曲率半径 图5 D0等深面内收/发截线Fig.5 Receiving and sending intercept lines in the D0 isobaric plane (6) 圆锥曲线最小曲率半径为圆锥顶点到截平面的距离与圆锥半顶角正切值的乘积[22],因此,ρR、ρT为收/发传感器到波束脚印深度与收/发锥面半顶角的乘积 (7) 式中,D表示传感器吃水深度。将式(7)代入式(6)即可得到MR、MT。 式(6)—式(7)的推导基于传播曲面为圆锥面,因此MT和MR并非精度ε0下的严密推导结果。但式(6)中的不等号可在一定程度上保证估算的有效性。大量试验表明,一般情况下,当截点间距小于MT和MR时,以上计算相对严密迭代计算偏差小于ε0。 2.1.2 迭代区间初值和矫正 合理设置迭代角度初始区间(αR1,αR2)、(αT1,αT2)和深度初始区间(D1,D2),可减少迭代次数。因此,本文根据MT和MR,估算角度区间半径rαR、rαT和深度区间半径rd (8) 设置αR1、αR2、αT1、αT2、D1、D2的初值为-rαR、rαR、-rαT、rαT、D0-rd、D0+rd,对αT1、αT2和αR1、αR2对应的4个矢量声线跟踪,保留其在D1和D2等深面内截点,其可能的分布如图6所示。图6(a)和图6(b)中发射截线和接收截线不相交,需调整初始角度αR1、αR2、αT1、αT2。对于图6(a)情况,按比例向αT2方向平移(αT1,αT2);对于图6(b),向αR1方向平移(αR1,αR2);最终收敛情况下截点分布情况如图6(c)所示。 图6 截点分布矫正角度范围Fig.6 Correction angle range of intercept 由于声线跟踪至少需要发射矢量方位角θT和俯角φT、发射声线单程传播时间tT[12,23]。本文利用插值计算以上参数,避免多次迭代和声线跟踪,提高算法效率。 2.2.1 声线跟踪参数插值函数建立 为了分析影响发射矢量方位角φT和单程传播时间tT的主要参数,进行如下假设:发射扇面垂直向下;接收传感器位置不变;接收传感器无姿态;水体无折射。 图7 扇区内参数关系Fig.7 Parameter relationship in the sector (9) (10) 本文等间隔选取n+1个点,建立扇区内tR/tT、φT的拟合函数如式(11)、式(12)所示 (11) (12) 图8 平坦、倾斜、曲线地形下多项式拟合残差Fig.8 Polynomial fitting residuals under flat,sloping,and curved terrain 2.2.2 参数插值及位置归算 本文在南海某区中深水和浅水各选择两条交叉线,测量仪器为Kongsberg EM302,地形如图9所示。其中图9(a)为浅水区,测线1水深180~200 m,东南-西北方向,面积约4.5×106m2,共2209 ping;测线2(图9为部分)水深160~240 m,西南-东北方向,共16 064 ping;两条测线每ping均432个波束,4扇区,交叉区域约1×106m2。图9(b)为中深水区,测线3水深900~1400 m,西南-东北方向,面积约1.8×108m2,共2630 ping,测线4(图9为部分)水深900~1600 m,西北-东南方向,共2 362 ping;两条测线每ping均432个波束,8扇区,交叉区域约为5×107m2。 图9 测线地形图Fig.9 Survey line topographic map 数据预处理步骤包括:声速剖面等数据质量控制和船文件编辑等。归算使用相同的原始数据、声速剖面、船文件,并分为3种方法:①Caris使用HIPS and SIPS11.1中Georeference Bathymetry模块的有声速无潮位模式;②本文算法;③顾及姿态及声线弯曲的归算模型[8-9](下称传统算法)。后两种方法均经过波束脚印相对传感器偏移量计算,坐标转换等步骤。下文对比3种算法在交叉测线的公共覆盖区内交叉点精度差异;本文算法与Caris同号波束点的互差;本文算法与Caris平均单个波束的运算时间,以验证本文算法的有效性和运行效率。 在测线1和测线2、测线3和测线4的公共覆盖区中各选择13 200个交叉点(一条测线的中央波束与同组另一条测线的交点)。基于3种方法的归算结果,在浅水区和中深水区分别计算各测线在交叉点处深度,统计测线1-2,测线3-4交叉点深度差异(表1)。 表1 交叉线公共覆盖区交叉点深度差异 由表1可知,交叉点深度绝对差异均值、绝对差异标准差、相对差异均值3种统计结果的表现为:在浅水区,本文算法与Caris相近,差异小于12%,且本文算法绝对差异均值更小,但标准差和平均相对差异略大;而传统算法差异均值大于本文算法60.0%,差异标准差大于本文算法10.0%。在中深水区,本文算法与Caris结果相近,差异小于2.5%;传统算法差异均值大于本文算法60.1%,差异标准差高于本文算法124.1%。 这表明,在浅水区,本文算法、Caris计算精度接近,传统算法的计算精度略低;在中深水区,本文算法和Caris计算精度相近,传统算法精度显著偏低。这可能是由于随着测量深度增加,收发传感器间距离增大,传统模型下的波束入射角和发射中心误差增大,导致计算精度偏低。统计结果中,中深水区差异并非0均值分布,这主要是由于此地区的声速剖面数据质量不高,导致边缘波束向两侧翘起,以及较大的地形起伏导致的精度不均一。 浅水区使用测线1,中深水区使用测线3,统计本文算法与Caris的同号波束计算结果互差(表2),并形成偏差频率分布条形图(图10)。 由表2可知,在浅水区,偏差均值为5~7 cm,偏差标准差为3~5 cm,相对偏差小于0.35‰Z;在中深水区,偏差均值为7~13 cm,偏差标准差为5~14 cm,相对偏差小于0.11‰Z,符合相关规范[25]。由图10可知,浅水区,90%以上的偏差集中在0~10 cm;中深水区,90%以上的偏差集中在0~30 cm。这表明本文方法计算结果与Caris具有较好的一致性,验证了本文算法的有效性。 图10 本文算法与Caris同号波束脚印偏差Fig.10 The beam footprint calculate by algorithm in this paper and Caris deviation 表2 同号波束脚印位置较差 图11 归算差异与接收角度Fig.11 Reduction difference and receiving angle 为验证本文算法有较高的运算效率,分别统计浅水区测线1和中深水区测线3的全部波束,计算本文算法与Caris单个波束平均运算时间,以及本文算法的平均声线跟踪次数(表3)。由表3可知,声线跟踪作为算法中耗时占比较高的部分,本文算法的平均次数略高于传统算法的1次,低于NCCA模型的6~8次。在浅水区,本文算法效率相对Caris提高8.22%;中深水区,相对Caris提高35.21%。两区域效率均有一定程度提高,且中深水区相对浅水区效率提高更明显。 表3 单个波束平均效率对比 相比于传统模型、VCCA模型、NCCA模型,本文算法提出的传播曲面模型准确还原了波束脚印位置归算过程, 顾及了收发传感器的位置差异及收发传播时间不相等的问题, 理论基础更为严谨。在此基础上,通过迭代搜索和参数插值的方式显著减少声线跟踪次数,提高计算效率,实现基于传播曲面模型的高效位置归算。经实测数据验证,本文算法交叉线公共覆盖区交叉点误差与Caris相近;与Caris同号波束脚印归算结果较差,浅水区差异小于0.3‰Z,中深水区差异小于0.1‰Z;且两测区内运算效率相较Caris均有所提高。随着深度的增加,本文结果与Caris的相对偏差值,有一定程度的降低,且运行效率相对更高,深水区有更好的适用性。在测量原理相同,且已记录发射、接收指向角、双程时间等参数的多波束测深数据中,本文算法适用。


2.1 插值结点波束脚印位置归算


2.2 待插值波束脚印位置归算
2.2.1.1 φT、tR/tT插值函数建立




2.2.1.2 不同地形条件下多项式拟合残差


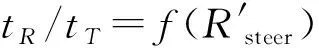


3 试验分析及讨论

3.1 交叉线公共覆盖区格网点差异对比

3.2 同号波束归算差异对比



3.3 位置归算效率分析
4 结 论
