结合区域增长与RANSAC的机载LiDAR点云屋顶面分割

赵 传，郭海涛，卢 俊，余东行，林雨准，姜怀刚

1. 火箭军指挥学院，湖北 武汉 430012； 2. 信息工程大学地理空间信息学院，河南 郑州 450001； 3. 海图信息中心，天津 300450

建筑物作为城市中最基本、最主要的组成元素，其三维模型在智慧城市建设、灾害评估、城市环境快速监测等领域有着广泛的应用[1-3]。作为一种可快速直接获取建筑物三维数据的技术，机载激光雷达(light detection and ranging,LiDAR)在近些年得到了长足的发展，并已成为建筑物三维模型重建的重要数据源之一。屋顶面作为建筑物结构的基本组成元素，有效地对其进行分割是利用机载LiDAR点云重建三维建筑物模型的关键问题之一[3-4]。尽管很多学者对屋顶面分割进行了深入的研究，也取得了一些成果，但由于现实场景中建筑物屋顶形状复杂、同一建筑物不同屋顶面大小差异较大、不同建筑物屋顶面数量不同，以及机载LiDAR点云固有的密度不均、噪声等多种因素的影响，导致屋顶面的有效分割仍然面临很大挑战[3-5]。

在过去的十几年里，大量的研究主要集中于提高三维平面分割方法的效率和稳健性，现有的平面分割方法大致分为5类：区域增长法、特征聚类法、模型拟合法、全局能量优化法和混合法[3-7]。

区域增长法(region growing,RG)通过逐步合并具有相似特征(如法向量、曲率等)的邻域点进行平面分割，原理简单，易于实现，且效率较高，在大多数情况下能得到较好的分割结果，但对于过渡平缓的平面，难以设置停止增长的阈值，容易出现过增长。虽然一些研究通过构建体素或超体素，计算体素的平面性，以平面体素和非平面体素中的单个点为基元进行混合增长[4,8-10]，可有效防止过增长，但如果体素大小设置不当，容易漏分割面积较小、狭长形的屋顶面。特征聚类法利用计算的点云特征，采用如meanshift[11-12]、k-means[13]、模糊聚类[14]、谱聚类[15]、DBSCAN[3,16]等聚类算法实现屋顶面分割，尽管基于特征聚类的方法在特征计算准确时能取得较好的结果，而且具有较高的效率，但点云特征的计算本就存在难以设置合适邻域的问题，此外，该类方法对噪声和异常值很敏感[6-7,17]。模型拟合法利用点云拟合预定义的模型方程实现分割，具有代表性的模型拟合法包括随机采样一致性(random sample consensus,RANSAC)和Hough变换(Hough transform,HT)[17]，两种方法对噪声和异常值具有稳健性，可以同时得到优化的模型参数，但也都对分割参数的设置十分敏感，相较而言，利用RANSAC能得到相对更好的分割结果[5,18-19]。HT将分割问题转换到参数空间，通过求解参数空间累计器局部最大值得到分割平面的参数，但通常比较耗时，且分割结果中容易出现伪平面[17]。经典的RANSAC通过随机选点构建初始平面[20]，其分割结果中也容易出现伪平面[6,17]，且在数据分布较为复杂时，效率将会明显降低[6]。为此，很多学者从不同方面改进了经典的RANSAC，如文献[21—22]改进了RANSAC的采样策略以提高其效率、文献[5，23]分别从采样基元和权函数两方面改进RANSAC以较好地解决分割结果中的伪平面问题。然而，RANSAC追求数学意义上的一致性，通过迭代的方式从点云中顺序分割平面，容易出现屋顶面竞争现象，且只能得到次优的分割结果。为了得到全局最优的分割结果，一些研究者将广泛用于图像领域的能量最小化方法引入点云分割中，如文献[6—7,17]。这类方法需要首先获取候选平面的参数，然后构建包含数据损失项、平滑损失项等损失项的能量函数，采用图割等算法实现能量最小化，从而得到分割结果。虽然全局能量最小化法可以得到全局最优的分割结果，能较好地解决屋顶面竞争现象，但其结果很大程度上依赖于候选平面的质量，且存在能量函数中各损失项的权重设置难、优化效率较低等不足。混合法结合多种方法进行平面分割，在流程设计合适的情况下可以有效地综合利用不同方法的优势，如文献[4]结合了区域增长、聚类和全局能量优化法，文献[24]结合了剖面分析、区域增长法，文献[25—26]结合了HT和RANSAC、文献[27]结合了RANSAC和全局能量优化法。

由于构建体素或八叉树容易导致漏分割屋顶面，且利用一种屋顶面分割方法通常难以得到较好的分割结果[16]，为了实现建筑物屋顶面点云的有效分割，本文以每个点为处理单元，提出一种结合区域增长与RANSAC的机载LiDAR点云屋顶面分割方法，以期提高分割结果的精度和方法的适用性。

1 原理与方法

结合区域增长与RANSAC的屋顶面分割方法以建筑物的机载LiDAR点云为输入，引入稳健的法向量估计方法计算点云法向量和曲率，以点与屋顶面的法向量夹角和点到屋顶面的垂距两个约束进行迭代区域增长，再利用RANSAC提取小屋顶面，并基于RANSAC计算内点的思想迭代合并屋顶面。方法主要包括可靠屋顶面片提取和面片优化两个步骤，其整体流程如图1所示。

图1 屋顶面分割流程Fig.1 Flowchart of roof segmentation

1.1 可靠屋顶面片提取

1.1.1 法向量和曲率计算

机载LiDAR点云包含丰富的几何信息，在点云处理过程中需要考虑邻域点的影响，因此现有的基于RG屋顶面分割方法通过选择一定范围的邻域点，采用构建协方差矩阵进行主成分分析(principal component analysis,PCA)的方式计算点云法向量和曲率[2,28]，然后设定法向量和曲率阈值进行增长。然而，由于点云具有分布不规则、密度不均、点与点之间没有拓扑关系等特点，因此难以选择合适的邻域用于构建协方差矩阵，此外，PCA实质是一种低通滤波器，会平滑尖锐特征，且其最小二乘的本质，使得通过PCA计算的结果对噪声十分敏感，这些因素都将导致计算的点云法向量和曲率不准确，造成利用法向量和曲率进行屋顶面分割难度的增加，以及分割结果质量的降低。

近年来，学者们在法向量估计方面已经取得了较多的研究成果，一些具有保持尖锐特征的稳健法向量估计方法相继被提出[29-32]。相比PCA，这些法向量估计方法可以估计更为准确的法向量，且具有更好的适用性和更强的抗噪性，估计结果受参数的设置影响更小。然而，现有的屋顶面分割算法大都仍然采用PCA计算点云的法向量，为了充分利用现有的稳健法向量估计结果，以降低区域增长分割屋顶面的难度，提高分割结果的精度，本文将稳健法向量估计方法引入屋顶面分割，采用效果相对更好的多法向量成对一致性投票方法(multi-normal pair consistency voting,PCV-MN)[31]计算点云的法向量和曲率。

1.1.2 迭代区域增长

理论上，在点云中所有点的法向量估计完全准确的情况下，通过判断种子点的邻域点与其法向量夹角进行增长就能得到较好的分割结果。然而，由于点云数据中不可避免地存在数据缺失、密度不均等现象，尽管PCV-MN可以得到更为稳健的法向量估计结果，其计算结果中部分点的法向量与真实值仍然存在一定的偏差，如果采用与现有基于RG的屋顶面分割算法相同的策略(以法向量夹角或曲率为增长准则)，则仍难以有效地适用于复杂程度不同的建筑物屋顶面分割，当夹角阈值设置较小时，增长的结果中会包含过多的屋顶面片，造成欠增长，设置过大，则容易导致过渡平缓的相邻屋顶增长为同一屋顶面，造成过增长。此外，现有的基于区域增长的屋顶面分割方法在每次增长后，仅对种子点集合进行判断(如果为空，则结束增长)，而未判断增长结果的可靠性，难以保证增长结果的有效性。

为了解决现有基于RG屋顶面分割方法的上述不足，本文提出迭代区域增长(iterative region growing,IRG)的策略，一方面，在每次增长时，不再以单个点之间的法向量夹角为准则，而是以点与增长平面的法向量夹角和点到增长平面的距离为准则，另一方面，在每次增长后，对增长的结果进行判断，以保证增长结果的可靠性。IRG的具体步骤如下：

(1) 输入建筑物机载LiDAR点云及计算的法向量n和曲率σ，设置所有点的初始状态为非种子点，标号L为0，种子点集Ss为空集，屋顶面标号rl为1，精化迭代次数it为0。

(2) 选择标号为0、状态为非种子点且具有最小曲率的点pi，作为当前增长的初始种子点，如果点pi不存在，则结束IRG，得到多个可靠屋顶面片的增长结果，否则将点pi的标号置为rl、状态标记为种子点，并将其加入Ss，选择Ss中的第一个点p1(其法向量记为np1)，利用式(1)计算初始平面参数npl，dpl

(1)

(3) 计算点p1的邻域点q与平面法向量的夹角θq以及到平面的垂直距离dvq，将满足式(2)的邻域点集Sng加入种子点集Ss，同时将Sng中所有点的标号置为rl，并从Ss中去除点p1，再重新选择Ss中的第一个点(仍记为p1)，重复该步骤，直到Ss为空，得到当前增长点集SL=rl(即所有标号为rl的点构成的集合)

Sng={q|(q∈Np)∧(Lq==0)∧(θq<θt)∧

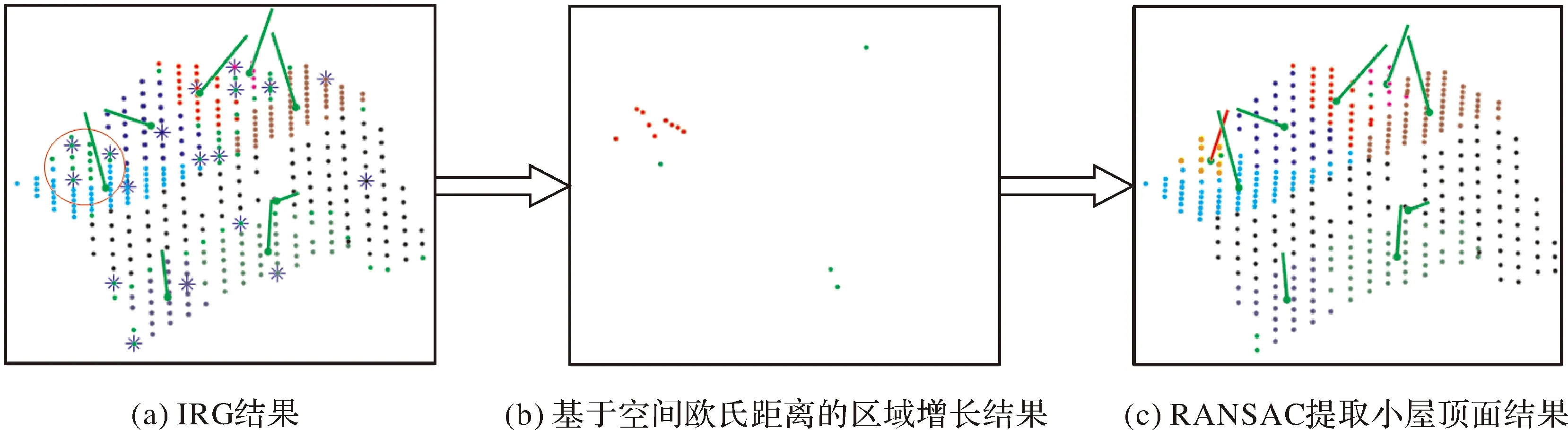
(dvq

(2)

式中，Np代表点p的邻域点集；θt、od分别为法向量夹角和垂直距离阈值(下同)。

(4) 判断精化迭代次数it是否小于阈值max_iter，是则令it=it+1，利用SL=rl构建协方差矩阵拟合平面，得到特征值和特征向量，进入步骤(5)，否则进入步骤(6)。

(5) 将SL=rl中所有点的标号置为0，令SL=rl=∅，根据协方差矩阵的特征值计算SL=rl点集的平面性[8]，判断拟合的平面是否可靠，如果可靠，则更新平面参数，返回步骤(3)，仍以当前增长最初选择的种子点重新增长，否则不更新平面参数，返回步骤(2)，重新选择种子点进行增长。

(6) 利用SL=rl进行基于欧氏距离的区域增长，以分离相邻平行的屋顶面(距离阈值deu根据经验设置为1 m，下同)，选取增长结果具有较多点数的类别作为IRG当前增长的结果，即保持这部分点的标号不变(为rl)，其余点的标号置为0，令it=0，rl=rl+1，返回步骤(2)。

为了直观地展示IRG的效果，选取一栋具有5个屋顶面的建筑物，用不同方案设置相同增长参数进行处理(其标准分割结果如图2(a)所示)：①每次增长后仅对种子点集进行判断，得到类似于现有基于RG的屋顶面分割算法(记为RG_0)；②分别设置最大精化迭代次数max_iter为1—4(记为IRG_1至4)。不同方案的处理结果如图2(b)—(f)所示(图中不同颜色代表增长的不同屋顶面，绿色短线为各增长屋顶面的法向量，蓝色星号点为增长时用到的初始种子点)。从图2(a)可以看出，该建筑物包含一个狭长屋顶面A，且由于其与B屋顶面的空间距离很近，导致A屋顶面所有点的法向量与B的法向量夹角均很小，因此RG_0完全过增长屋顶面A，且欠分割了屋顶面B(图2(b)所示)；从图2(c)—(f)可知，即使仅进行一次迭代精化，IRG也能分割部分屋顶面A的点，随着迭代次数的增加，屋顶面A可以较好地被分割，说明IRG可以有效解决欠增长，得到可靠的增长结果。

图2 区域增长结果对比Fig.2 Results comparison of region growing

1.1.3 不可靠小面片精化处理

在IRG过程中，所有建筑物点都可能成为增长时选用的种子点，而由于法向量计算结果存在一定的误差，因此会造成误增长(如图2(d)中左上角放大区域所示的小面片)，这些误增长的小面片(本文定义为小于3 m2的屋顶面)通常存在于不同真实屋顶面的相交处，其包含的点数较少且可能属于不同的真实屋顶面，因此需要进行合并或剔除。

对于任意误增长面片A，如果存在面片B满足其与A的法向量夹角小于θt，A中所有点到B的垂直距离小于od且欧氏空间距离小于deu，则直接将A合并至B，否则计算A中每个点到其他面片的垂直距离和欧氏空间距离，将各点归类为垂直距离小于od且欧氏空间距离小于deu所对应的面片，如果不存在满足条件的对应面片，则将其归类为未增长点。

1.2 面片优化

1.2.1 RANSAC提取小面片

从图2(c)—(f)可以看出，IRG无法完整地增长所有屋顶面，未被增长的点包括尖锐特征附近的点、噪声点以及部分小屋顶面，主要由于法向量计算不准确、真实场景中的建筑物屋顶具有十分复杂的结构和不同的大小，以及点云的一些固有特点等因素导致。为了防止漏分割小屋顶面，同时考虑到真实小屋顶面表现为局部范围内聚集的点，因此首先对未被增长的点进行基于欧氏距离的RG，然后利用RANSAC从每个增长结果中提取潜在的小屋顶面，并计算提取结果的平面性以保证其可靠性，过程如图3所示。由图3可以看出，IRG未能增长的小屋顶面(图3(a)红色圆圈所示)，通过欧氏距离的RG将其归为了一类，利用RANSAC可有效地提取该小屋顶面，如图3(c)中橙色点所示(红色短线代表其法向量)。

图3 RANSAC提取小屋顶面Fig.3 Illustration of small roof extraction by RANSAC

1.2.2 合并可靠屋顶面片

可靠屋顶面片提取的目的是尽可能多地得到可以表示所有屋顶面的面片，因此提取的面片数会大于实际屋顶面数，需合并属于同一屋顶面的可靠屋顶面片。不同于现有合并面片的方法，如文献[3]利用面片参数(仅能合并近似平行的面片，一旦面片参数不可靠，则无法合并)、文献[2]仅利用到面片距离的均值(容易造成过渡平滑的面片合并、近似平行的小屋顶面错误合并到大屋顶面)，本文基于RANSAC判断内点的思想进行迭代合并，具体步骤如下：

(1) 选取面片Ai，计算Ai与面片Ai+1，Ai+2，…，An法向量的夹角，如果存在面片Aj与Ai的法向量夹角小于阈值θt/2，或夹角小于θt且Ai、Aj面片的欧氏空间距离小于deu，进入步骤(2)，否则选择Ai+1，重复本步骤。

(2) 计算面片Ai中的所有点到面片Aj的垂直距离，统计距离小于od的点所占比例peri，计算面片Aj所有点到面片Ai的距离，统计距离小于od的点所占比例perj；如果peri和perj满足式(3)所示条件(即flag为真)，则将Aj包含的所有点加入Ai，实现将面片Aj合并至面片Ai，同时标记面片Aj为已合并

flag=(peri>0.5∧perj>0.5)|(peri>0.99∧perj>0.1)|(peri>0.1∧perj>0.99)|(peri+perj>1.2)

(3)

(3) 判断所有面片是否均不满足合并条件，如果是，则合并面片结束，否则去除所有已被合并的面片，利用合并后的面片包含的点重新拟合其平面参数，返回步骤(1)继续合并。

1.2.3 后处理

后处理的目的是将前面步骤中未能增长的点正确地归类到所属屋顶面，并通过局部邻域投票的方式处理屋顶面竞争现象。

在进行面片优化后，建筑物各屋顶面的大部分点都能得到正确分割，因此拟合的平面方程较为可靠。对于结构简单的建筑物，只需要计算未增长点到各个屋顶面的垂直距离，选取最小距离所对应的平面即可。然而，一方面，未增长点中可能包含如烟囱等属于屋顶附属物的点，但这部分点理论上不属于任何屋顶面，另一方面，屋顶面为有限范围内的平面，部分未增长点可能到某屋顶面所在平面的垂直距离很近，但空间距离却较远，因此并不能归为垂直距离最小的屋顶面。考虑到上述因素，在计算未增长点到各屋顶面的垂直距离后，选择垂直距离小于od且具有最小空间距离的屋顶面作为未增长点所属屋顶面，实现对其归类。

尽管在前面的处理过程中，均以法向量和垂直距离对每个点进行了约束，但部分屋顶面点仍存在竞争现象，因此需利用邻域信息进行处理。本文采用文献[3]中处理屋顶面竞争的策略，即以局部邻域范围内涉及的屋顶面及到对应屋顶面的垂直距离构建权重函数，选择具有最大权重的屋顶面对所有点进行重新标记。

2 试验与分析

2.1 数据与评价标准

本文选取10栋具有不同复杂结构、不同屋顶大小的建筑物(分别记为B1—B10，其特点见表1)及与文献[32]相同区域的建筑物点云数据(影像及对应的点云如图4所示)进行试验，其中B1—B5和区域建筑物点云、B6—B10分别为Vaihingen地区[34]和科罗拉多博尔德分校地区[35]的部分机载LiDAR点云，其屋顶结构相对于B1—B5更加复杂，同一建筑物的屋顶面个数更多且屋顶大小差异更大。

表1 10栋有代表性建筑物的相关信息

图4 区域建筑物影像及点云Fig.4 Image and point cloud of the region

试验中的参考屋顶面分割结果为利用CloudCompare软件(http:∥www.cloudcompare.org/)，通过结合影像人工分割的方式得到。为了定量评价屋顶面分割结果，首先利用文献[36]的方法，通过求分割结果的各屋顶面与参考数据中屋顶面的交集比(大于50%)构建一一对应的关系，然后采用文献[7]中的完整率和正确率进行评价，计算方式如式(4)所示。文献[7]在计算完整率和正确率时，以单个屋顶面为统计基元，但即使两个屋顶面是一一对应的关系，其中也必然会包含部分误分割和漏分割的点，因此本文从单个屋顶面和单个点两个层面分别评价分割效果，即式(4)中统计TP、FN和FP的基元是屋顶面或单个点，记两个层面评价得到的指标分别为comp1、corr1和comp2、corr2

(4)

式中，TP代表正确分割的基元数;FN代表漏分割的基元数;FP代表误提取的基元数。

2.2 结果与分析

为了验证本文方法的有效性和适用性，对比了经典的RANSAC、结合主成分分析的区域增长(region growth+principal component analysis,RG_PCA)[37]、交叉线元增长(cross-line element growth,CLEG)[24]和边界重标记(boundary relabeling,BR)[4]4种方法，各方法参数的设置见表2。其中，RANSAC和RG_PCA采用开源的PCL(point cloud library)中的已有实现，参数通过经验设置；CLEG和BR由原文作者提供可执行程序，相关关键参数通过多次试验确定最优值；本文法向量通过文献[31]作者提供的源代码计算。

表2 不同方法的关键参数设置情况

2.2.1 分割效果分析

利用5种不同方法对试验采用的建筑物点云数据进行分割，其结果如图5和图6所示，其中黑色点代表噪声点或未分割点，其他不同颜色代表分割的不同屋顶面。

对于细小狭长屋顶面(如参考分割结果B1中箭头所指屋顶面)，RANSAC虽较好地分割了此屋顶面，但由于RANSAC仅是追求数学意义上的一致性，且迭代分割屋顶面，分割过程存在先后顺序，因此出现了明显的屋顶面竞争现象；RG_PCA虽能分割该屋顶面左侧部分点，但由于PCA计算的法向量不准确，未能成功分割该屋顶面右侧的点；CLEG未能分割出该屋顶面，可能的原因是参数设置不当，此外由于CLEG基于交叉线元增长，未考虑点云法向量，因此也出现了明显的屋顶面竞争现象；BR将此狭长屋顶面完全错误分割到相邻的屋顶面，主要因为BR首先将点云以体素的方式进行表示，当体素正好位于不同屋顶面交界处时，不满足平面性，会被分解成单个点分割到其他屋顶面；本文方法采用点为处理单元，且采用稳健的法向量估计方法得到更加准确的法向量，能够较好地分割此狭长屋顶面。类似的B1情况如图6区域建筑物中参考分割结果的黑色框AB放大区域所示，但B框中的红色屋顶面距离其他屋顶面较远，易于分割，除CLEG外，其他几种方法都能较好地分割该屋顶面。

图6 区域建筑物屋顶面的分割结果对比Fig.6 Comparison of roof segmentation result of regional buildings

对于过渡平缓且相交的不同屋顶面(如参考分割结果B2、B3和B7中黑色箭头所指屋顶面)，RANSAC可以分割结构相对简单的B2中的所有屋顶面，但结果较为杂乱，对于结构相对复杂的B3和B7，RANSAC无法有效地分割过渡平缓的屋顶面，且结果更杂乱；由于PCA具有平滑尖锐特征的作用，且在尖锐特征处(尤其是多个屋顶面相交处)，通过PCA计算的法向量不准确，因此RG_PCA未能分割B2、B3和B7中过渡平缓的屋顶面，同时在尖锐特征处，会漏分割较多的屋顶面点，如RG_PCA对B3、B7分割结果中的黑色点所示；CLEG欠分割了B2中过渡平缓的屋顶面，但同样未能分割B3和B7中过渡平缓的屋顶面，同时还漏分割了B3中的多个屋顶面(图中黑色点所示)，出现了屋顶面竞争的现象，可能的原因包括参数设置不当以及方法的分割效果依赖于种子交叉线元的选取；尽管BR未能有效地分割B2中过渡平缓的屋顶面(两屋顶面之间的夹角约为7.8°)，但有效地分割了B3中的过渡平缓屋顶面(夹角约5.5°)，主要原因在于B3中两个屋顶面并未直接相连，BR分割时构建了体素，可以一定程度上防止增长时合并过渡平缓的屋顶面，而对于B7中的过渡平缓的屋顶面，CLEG和BR均得到了欠分割的结果(4个过渡平缓的屋顶面分割为2个)；本文方法较好地分割B2、B3中的过渡平缓屋顶面，对于B7中过渡平缓的4个屋顶面，本文方法也存在欠分割的情况，但相对CLEG和BR的结果更好(4个过渡平缓的屋顶面分割为3个)。

对于过渡平缓且存在较小高度差的不同屋顶面(如参考分割结果B4左上角和图6右下角箭头所指屋顶面)，由于屋顶面之间法向量夹角较小，且高度差甚至小于平均点间距，即使是人工分割，也存在一定难度，因此几种方法均未能得到准确的分割结果，本文方法在远离屋顶面相接处，可以分割部分屋顶面点，主要因为采用了更稳健的方法计算了法向量，且同时采用法向量和垂直距离作为约束进行增长和分割。

对于结构相对简单、屋顶面之间层次分明的建筑物(如B5、B6和图6中大部分建筑物)，几种方法均能得到较好的分割结果，但RANSAC仍存在竞争现象，而RG_PCA则在屋顶面相交区域存在较多的漏分割点，相较而言，CLEG、BR和本文方法分割结果更为准确，彼此差别不大；随着屋顶面拓扑关系复杂度、个数的增加，RANSAC和RG_PCA的分割效果明显下降，CLEG出现了漏分割和屋顶面竞争现象，BR和本文方法分割结果较好。

对于面积很小的屋顶面(如参考分割结果B2—B4、B8—B9和图6中红色箭头所指屋顶面)，几种方法都存在漏分割的现象，但相对而言，本文方法的结果中漏分割的小屋顶面更少；对于非平面屋顶面(如参考分割结果B9中的弧形屋顶面)，RG_PCA通过法向量夹角和平滑度约束，可以有效分割该曲面屋顶面，试验中输入RANSAC的模型为平面方程，CLEG、BR和本文方法均针对平面屋顶面分割而设计，因此这4种方法仅能分割平面屋顶面，对于非平面屋顶面，会过分割为多个平面块，类似的情况如参考分割结果B4右侧黑色箭头所指屋顶面和图6中矩形框D所示屋顶面。

2.2.2 定量评价与分析

为定量评估不同方法的屋顶面分割性能，分别以屋顶面和单个点为单元统计了分割的完整率和正确率，如表3所示。

表3 以单个屋顶面/单个点为评价单元的精度统计结果

由表3可知，仅以一种单元统计评价分割结果不能较好地反映不同方法的分割性能，如表3中CLEG、BR和本文方法分割部分建筑物屋顶面的正确率和完整率均能达到100%，但实际上有部分点属于漏分割和错分割，因此以点为单元进行统计时，所有方法的正确率和完整率均不能达到100%，这与实际情况相符。对比表3中同一方法对不同建筑物屋顶分割的精度统计结果可知，5种方法对屋顶相对简单的建筑物分割的结果(B1—B5和区域建筑物)优于其对具有复杂屋顶建筑物分割的结果，随着屋顶拓扑关系复杂度的增加，以屋顶面为单元的精度统计结果中，RANSAC和RG_PCA的完整率和正确率都有明显下降，CLEG、BR和本文方法的指标也稍有降低；对于建筑物B8，本文方法的完整率高于其他4种方法，但正确率低于CLEG和BR，主要是因为本文方法分割结果中存在较多的小屋顶面，在参考分类结果中这些小屋顶面属于同一屋顶面，导致较多的误分割，而CLEG和BR则漏分割了这部分屋顶面(如图5(h)中放大区域和红色箭头所指屋顶面)；对于建筑物B9，存在与B8类似的情况，具有较多的小屋顶面(如图5(i)参考分割结果中红色箭头所指屋顶面)，此外，B9中的非平面屋顶面也是导致正确率较低的一个原因。然而，5种方法以单点为单元统计的完整率和正确率变化不大，这主要是由于5种方法都能较好地分割建筑物的主要屋顶面，即式(4)中的TP较大，使得计算的完整率和正确率变化不大。

综合分析表3的精度统计结果可知，在以屋顶面和单点为单元进行精度统计的情况下，本文方法的完整率和正确率总体上均优于其他4种方法。

3 结 论

为实现屋顶面的有效分割，本文提出了一种结合区域增长与RANSAC的机载LiDAR点云屋顶面分割方法。利用多个有代表性的建筑物点云和区域建筑物点云进行了分割试验，综合分析分割效果和结果的定量评价可知，相较于对比的4种方法，本文方法在得到更高分割精度的同时，可以有效地分割具有不同大小、形状和复杂程度的建筑物屋顶面，适用性更强。与现有方法类似，本文方法需要设置少数几个参数，但都具有明确的含义，因此易于设置。此外，本文方法的分割精度可以随着法向量估计算法的发展得到进一步的提升。然而，本文方法未能考虑面片优化阶段提取的小面片可能存在错误的情况，且在分割结果中不同屋顶面的相交区域仍存在部分屋顶面竞争现象，因此，下一步的研究需要设计有效的策略剔除在面片优化阶段可能提取的错误小面片，同时引入全局能量优化的方法以更好地解决屋顶面竞争的现象，进一步提高分割结果的精度。