时序Sentinel-1TOPS模式SAR数据精配准

马张烽，蒋 弥，丁琪瑄

1. 河海大学地球科学与工程学院，江苏 南京 211100； 2. 中山大学测绘科学与技术学院，广东 珠海 519082

Sentinel-1合成孔径雷达(SAR)卫星具有重访周期短(A、B组合为6 d)和覆盖范围广等优点，近年来已被广泛应用于成像大地测量和地球物理学研究。其中，干涉宽幅模式采用逐行扫描地形观测(terrain observation with progressive scanning,TOPS)[1-2]作为标准SAR成像模式，可以同时获得3个子条带，幅宽达250 km。然而在TOPS模式下，相邻burst影像(图1)高多普勒质心频率差(约5000 Hz)对方位向配准误差十分敏感。理论上，TOPS模式数据方位向配准精度需小于0.001像素，才能避免干涉图相位不连续或相位跳变现象。现有研究表明，采用精密轨道的几何粗配准[3]和增强谱分集(enhanced spectral diversity,ESD)技术[4]是实现高精度TOPS模式数据配准，消除相位跳变的有效手段。

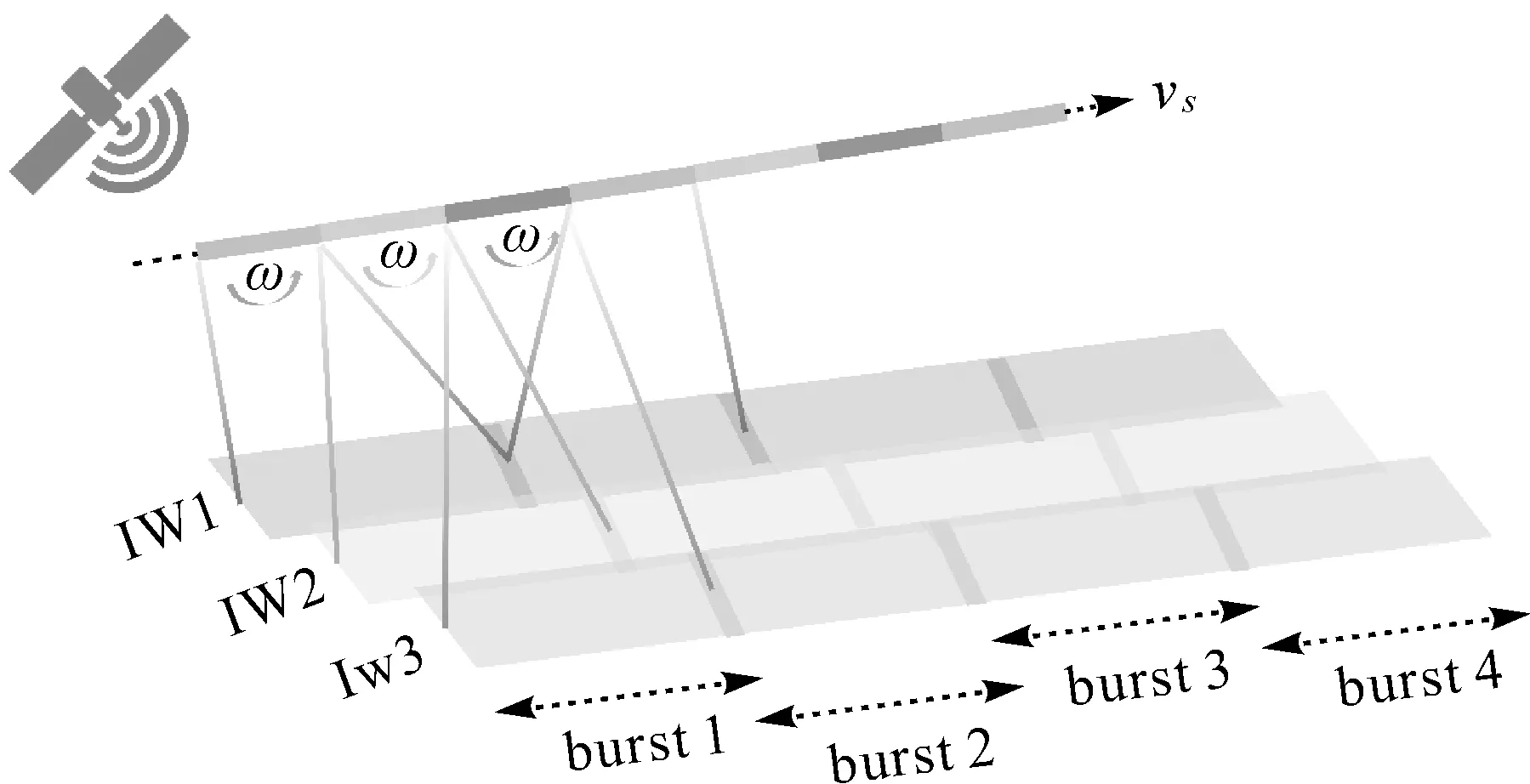
图1 TOPS成像Fig.1 Description of TOPS imaging geometry

受地形起伏影响，传统低阶多项式拟合影像配准方法无法满足配准偏移量为恒量的假设前提，导致非平稳信号的出现[5]。随着GNSS定轨技术的成熟以及SAR影像聚焦理论的发展，联合SAR精密轨道信息和外部数字高程模型(digital elevation model,DEM)进行粗配准是相对有效的方法[6-9]。假设忽略电离层效应和方位向地表形变的相位贡献，粗配准后的方位向配准误差主要与轨道误差、SAR传感器钟差误差相关[10]。这些误差均产生系统性的方位向偏移量，需要进一步精配准操作消除残余的方位向偏移量。

ESD技术是消除系统性方位向偏移量的有效方法。从已有研究来看，文献[11]将ESD技术与谱分集[4]技术进行了比较，利用TerraSAR-X TOPS模式数据证明了ESD的优越性能。文献[10，12]对Sentinel-1TOPS模式数据配准进行了详尽分析，论证ESD技术具有普适性。在国内，文献[6—7,13]详细阐述了ESD技术的误差敏感度，并定量证明了精密轨道对ESD相位估计的重要性。与分频干涉法[14]类似，ESD利用上下频带(每个burst影像长度的8%)之间的重叠区干涉相位差来估计方位向残余偏移量。因此，ESD的估计精度十分依赖干涉相干性[15]。就时序SAR配准而言，由于干涉对遭受的时空去相关作用不同，ESD的估计精度也不同。在低相干性场景，ESD技术可能完全歪曲估计结果并形成粗差，从而在数据堆栈中造成误差传播，降低整个数据集的配准精度。

最大化时间网络相干性是改善ESD估计精度的有效手段。类似于InSAR时序分析，小基线技术仍然是降低时空去相关的主流方法。例如，文献[10]提出了一种序贯时间网络ESD方法(network ESD，NESD)，即通过时间去相关指数衰减模型将最邻近时刻的影像相连，以便减少时间去相关对时序配准误差的影响，最后对网络进行整体平差。然而，这种方法无法适用于因环境变化导致的相干性突变(由于气候条件的影响，如雪和降水)。文献[15]提出的MST-ESD(minimum spanning tree based ESD)方法通过构造最小生成树来克服这种突发的相干损失，但由于缺少冗余观测，平差过程中解的稳定性可能依赖于研究区的整体相干性和其他估计手段。

综上所述，目前的时序TOPS模式数据配准方法无法兼顾相干性和多余观测。虽然小基线方法可以提供多余观测，但是网络中边(干涉对)的数量是根据阈值试探性确定的，过大的阈值易增加低相干干涉对，而过小的阈值易形成隔离子集。为解决这一问题，本文在图论框架下使用Bellman-Ford单源最短路径算法最大化时间网络的相干性并确保多余观测。考虑到经验性阈值选取的局限性，本文提出在先验序贯网络的基础上构筑任意两个TOPS模式影像的最短路径，在包含N幅影像的堆栈中，从N(N-1)/2个干涉集合中挑选出相干性较高的差分干涉子集，并确保网络的全连通性。通过模拟和实测数据证明，本文方法可显著提高ESD估计精度，进而改善整个时序TOPS模式数据集配准精度。

1 增强谱分集技术

如图1所示，连续burst之间独立成像且存在8%重叠区域。因此在干涉处理时，将方位向上两个相邻burst的重叠区域分为前后视影像，即将上一个burst影像的重叠区域视为前视影像，将下一个burst影像的重叠区域视为后视影像。通过计算前后视影像干涉相位差，并结合估计的多普勒质心频率差解算出burst的方位向残余偏移量，进而实现影像精配准[16]。其中，连续burst之间的多普勒质心频率差Δfovl≈5000 Hz，这使得式(1)中方位向配准时间误差Δt的微小变化会引起干涉相位差(ESD相位)φESD的大幅变化

φESD=2πΔfovlΔt

(1)

该现象说明配准误差对相位变化十分敏感，可以通过反算ESD相位来获得高精度配准时间误差。任一像元点P的ESD相位φESD,P可通过两次差分得到

(2)

式中，mi,p和si,p分别表示第i个主辅burst单视复数影像；mi+1,p和si+1,p分别表示第i+1个主辅burst单视复数影像；上标*表示复共轭算子。基于Sentinel-1高精度轨道姿态控制，ESD相位通常小于一个周期的相位变化，所以像元点P的ESD相位φESD,p无须进行相位解缠，而是通过周期图进行估算[12]

(3)

(4)

假设两个burst干涉图的重叠区域具有相同去相干机制，则Δx的精度可以通过相位噪声标准差σφ来衡量[10,15,17]

(5)

σΔx和γ的关系如下

(6)

图2展示了配准精度σΔx与样本数n和干涉相干性γ的关系。可以看出，当重叠区样本数n固定时，相干性将明显影响TOPS模式数据配准精度。

图2 ESD在40万、400万和4000万个相干像元点下的配准偏移量理论精度Fig.2 Theoretical azimuth co-registration accuracy of ESD under four hundred thousand,four million and forty million coherent pixels respectively

2 时序TOPS模式数据精配准算法

2.1 Bellman-Ford单源最短路径算法

最短路径是图论研究的经典问题，旨在寻找图中两节点间的最短路径并求得该路径下各边的最小权值总和。针对这类问题，本文采用Bellman-Ford单源最短路径算法。其基本思想是运用迭代法对所有边进行松弛操作，并由此更新起始节点到其他节点的最短路径值，直到获得最优解时迭代停止[18-22]。

在最短路径问题中，常用无向图G=(V,E,w)表示不含负回路的网络，其中V={v1,v2,…,vN}为节点集(影像序列)，E为G的边集(干涉组合)，w为G中的权矩阵(与相干性有关)。Bellman-Ford算法通过松弛操作推测V中所有节点最短路径的层次，并逐层生成以起始节点v1为根的最短路径树。松弛操作过程中，边集E的每次遍历是基于前一次遍历对当前遍历的部分节点的最短路径值进行更新。在第k次遍历中，最短路径层次为1～k-1的节点均已确定，此时最短路径层次为k的节点由最短路径层次为k-1的节点获得。由于最短路径不包含回路，(v1,vj)最短路径层次最高为N-1，因此算法最多循环N-1次。

Bellman-Ford算法的具体步骤如下：

(1) 对起始节点v1与节点vj的距离进行初始化。令起始节点v1到自身的距离d(v1)=0，起始节点v1到其他节点vj的距离d(vj)=+∞。此时(v1,vj)最短路径值d1(j)恰好等于起始节点v1与节点vj相连的单边距离

d1(j)=w1j(1≤j≤N)

(7)

(2)进入循环。循环下标为k，节点vj在第k次循环中到起始节点v1的距离为dk(j)。在循环内部，遍历边集E的每条边并进行松弛计算

(8)

(3) 当所有节点均满足dk(j)=dk+1(j)(k≤N)时，dk(j)即为(v1,vj)的最短路径值，此时循环结束。由式(8)可以看出，距离的度量实际上通过权w来实现，而权w就是与相关性有关的量。

2.2 InSAR时间网络

用上述Bellman-Ford方法构建InSAR时间网络的方法由以下3个步骤组成：①确定起点和终点;②从边集合中挑选出每个起点和终点的最短路径;③删除重复的边并形成网络。

在步骤①中，起点和终点可以通过小基线集合事先确定。本文采用顶点度数为4的序贯网络中所有边的起点和终点(vi,vj)作为先验(图3)。假设几何配准后的N景SAR影像按照时间升序排列V={v1,v2,…,vN}。步骤②从带权函数w:E→R的加权无向图G=(V,E)开始，找到从起点vi到最终vj之间最小权重的路径。E是所有可能边的集合,即N(N-1)/2个干涉图的平均相干性。根据Bellman-Ford算法，可以从E中挑选出经过(vi,vj)相干性最高的干涉组合。在步骤③中，重复步骤②直至所有起点vi和终点vj被遍历。在删除重复的干涉对之后，获得优化的干涉子集。图3概括了时间网络优化的具体过程。可以看出，增强后的时序网络能够使低质量的影像相互连接，因而比小基线中的经验阈值更加可靠，避免后者可能产生的孤立子集。与最小生成树方法相比，使用Bellman-Ford算法可以提供更多的多余观测或形成闭合环，这保证了在最小二乘平差过程中获得更高的估计精度。

图3 时间网络优化流程Fig.3 Flow chart of temporal network optimization

2.3 BF-ESD算法

将ESD技术与上述时间网络联合，可得到时序TOPS模式数据集配准算法，主要步骤为：

(1) 根据公共主影像的SAR几何，采用外部DEM和精密轨道信息将N景SAR数据进行几何配准。

(2) 用基于第2类统计的相干性估计量估计burst影像重叠区的样本相干性[21]，获得N(N-1)/2景干涉图的平均相干性。

(3) 用Bellman-Ford算法建立兼顾相干性最大化和多余观测的时间网络。

(4) 在使用式(2)—式(4)估计时间网络上每个干涉对的方位向偏移量之后，用加权最小二乘估计器获得时序数据集关于公共主影像的偏移量。

在后续的试验章节中本文的方法简写为BF-ESD算法。

3 结果与讨论

本文通过模拟数据和真实数据对BF-ESD的性能进行了评估和精度验证，并与现有的NESD和MST-ESD两种时序配准方法进行对比分析。

3.1 模拟试验

3.1.1 时序TOPS模式数据模拟

首先采用蒙特卡罗模拟试验评估时间网络对方位向精配准的影响。与前述研究类似，在复圆高斯模型的假设下，本文通过复圆高斯矩阵和复协方差矩阵的哈达马内积来模拟SLC时间序列[12,23-25]。在SLC模拟过程中，采用指数衰减去相关模型模拟复协方差矩阵中的非对角元素

(9)

式中，γi,j表示第i与j个SLC影像之间的相干系数。γ0=0.5和γ∞=0.1分别表示短期和长期相干性。γ0的物理意义是当时间基线ti,j趋于0时相干性的初值，而γ∞表示随着时间基线趋于无穷大，相干性衰减到的最小值。数值上，γ0=0.5表征了低相干场景，而γ∞=0.1模拟了相干性估计的偏差，即在纯噪声的环境下的相干性估计值并不为0。t=50 d表示与相干性衰减速度有关的量。为了凸显真实场景中突发的相干性损失，本文对协方差矩阵的非对角元素添加了[0,1]区间的随机信号。

式(2)需要两个burst干涉图的差分，因此在试验中用相同的协方差矩阵和不同的复高斯随机数模拟两组N=30的时间序列，并在差分干涉图中随机添加区间在[-0.02,0.02]像素之间的相位贡献。时序影像的获取间隔定义为12 d，其中假设第1景影像为主影像。为满足ESD技术的假设条件，线性形变速率设置为0。在每次模拟试验中，用于估算协方差的样本设置为100，从而减少样本复协方差矩阵估计对网络解算的干扰，强调时间网络的重要性。为公平比较，除了时间网络的差异，3种配准方法的相位和相干性估计量均相同，所使用的估计参数也相同。

3.1.2 分析与讨论

图4是10 000次蒙特卡罗的试验结果。将各配准方法估计的偏移量的方差除以基于单主影像配准的偏移量的方差之后转换成分贝(dB)，获得相对方差。相对方差值越小，说明配准精度越高。可以看出，本文提出的BF-ESD方法由于最大化相干性并包含多余观测，得到的方差最小。相比之下，MST-ESD中的最小生成树的估计结果最差。结果是可以预料的，因为在低相干场景中缺少多余观测，无法获得稳健的平差结果。NESD中的序贯网络虽然增加了多余观测，但包含了相对低质量的干涉对，因而精度低于BF-ESD。BF-ESD在所有时间序列数据中都有最小方差，说明该方法具有普适性，可获得更高的配准精度。

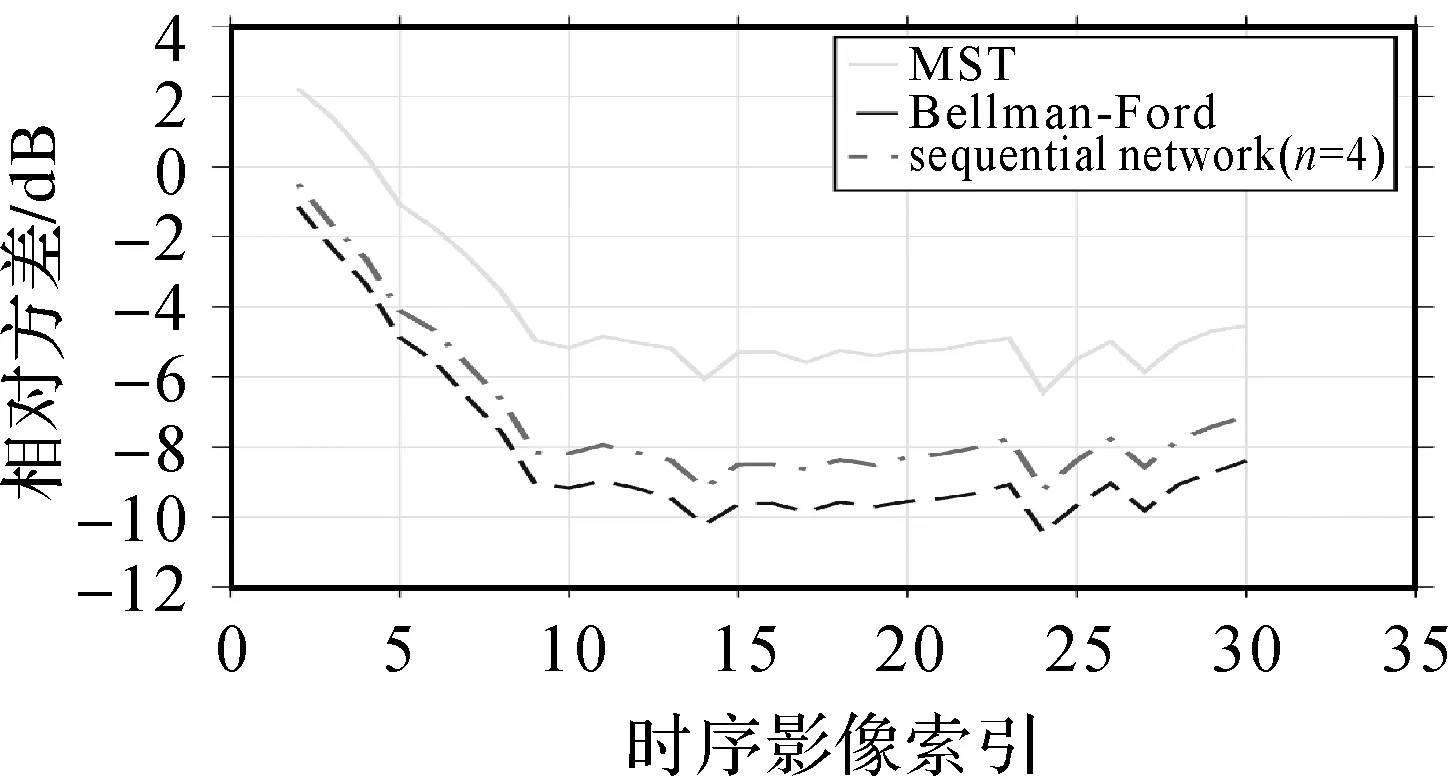
图4 10 000次蒙特卡洛模拟试验的配准偏移量相对方差Fig.4 The relative variance of azimuth offset after 10 000 times Monte Carlo simulation

3.2 真实数据验证

3.2.1 Sentinel-1 TOPS模式数据处理

选用2019年1月至2020年1月的31景Sentinel-1 TOPS模式影像(track84,frame110)，并选用覆盖了关中平原大部分区域的IW2和IW3两个子带。覆盖区属于温带季风气候区和亚热带季风气候区的过渡地带，年平均降水量约561 mm，平均湿度为69.6%，植被较茂盛，地形包含平原峡谷，具有部分相干性条件优良的裸地。选取该研究区的主要依据是气候与地貌条件使得不同干涉对存在干性差异，进而在执行图论算法时能够挑选出优质干涉组合、最大化时间网络的相干性。相反，相干性过高(如沙漠、城市)或完全去相关的区域(如中国西南部地区)均不能体现出算法的优势。这是因为时间网络上的干涉组合相干性对比度不强，各路径的最小权值接近，因此不能从本质上改善网络质量。

在几何配准之后，将所有SLC影像进行干涉组合(图5)，包括NESD中的序贯网络(n=4，图5(a))、MST-ESD中的最小生成树(图5(b))，以及本文提出的Bellman-Ford网络(图5(c))。对图5中每个干涉对，采用式(2)—式(4)估计ESD相位和方位向偏移量，并用加权最小二乘平差获得关于公共主影像(第1景)的偏移量。与模拟试验相同，除时间网络之外，所有方法均使用了相同的相干性估计器、相位估计器以及估计参数(7×7规则窗)。

图5 NSED、MST-ESD和BF-ESD的时序网络Fig.5 Temporal network of NESD,MST-ESD and BF-ESD

为定量评定各算法的精度，首先利用各时间网络估计30个辅影像的方位向偏移量。然后对其校正并重采样获得配准序列。最后将配准序列再次进行ESD估计，获得方位向偏移量。运用此法，对每一种网络进行50次重复试验，每次试验都基于前一次配准序列。最终获得的偏移量标准偏差越小，说明算法越稳定，精度越高。

3.2.2 分析与讨论

由图5可以看出，本次试验研究区的相干性低，平均相干性约为0.2。序贯网络包含的干涉对最多，导致网状结构复杂且包含相干性低的边。最小生成树挑选了所有干涉对中相干性最高的子集，然而受限于高相干点数量，最小生成树不能形成闭合的网络。相比之下，Bellman-Ford网络不仅剔除了序贯网络中相干性低的边，同时保证了网络的闭合性，这在2019年4月至2019年8月的子集中更为显著。

图6展示了BF-ESD方法在方位向偏移量纠正前后的对照。可以看出，图6(a)中左下角的相位不连续在图6(b)BF-ESD算法纠正之后被消除，说明BF-ESD算法能够有效去除方位向偏移量误差。图7展示了各网络下时间序列的方位向偏移量的标准偏差。从中可以看出，多余观测仍然是保证精度的主要前提，这可以从基于最小生成树的偏移量标准偏差中得以证明。其次，干涉对的质量仍然会影响偏移量估计的精度。在确保多余观测并改善观测质量的情况下，BF-ESD在所有配准的图像中均能得到最小的不确定性。定量地，基于最小生成树网络的偏移量标准偏差为0.001 9像素，NESD为0.001 3像素，BF-ESD为0.000 8像素。相比之下，BF-ESD方法估计精度远高于NESD方法以及MST-ESD方法，证明了本文方法的改进性能。

图6 配准误差纠正前后的干涉图对比(2019-04-24—2019-07-05，干涉图经过滤波处理以供视觉判读)Fig.6 Interferograms of 2019-04-24—2019-07-05 before and after correction of co-registration error using BF-ESD (both interferograms have been filtered for visual interpretation)

图7 时序数据集配准残余偏移量标准偏差Fig.7 Standard deviation of residual mis-registration

4 结论与展望

针对目前时序TOPS模式数据配准因去相干问题导致的精度衰减，本文提出了一种改善时间网络质量的方法。该方法利用图论中Bellman-Ford算法反复修正先验网络中低相干性的干涉组合，进而获得相干性更高的时间网络，并保留多余观测。高质量的时间网络能够减少因ESD估计误差导致的最小二乘误差传播，因而获得更精确的时间配准偏移量。本文结合模拟数据和真实数据对算法进行了可靠性评估并与现有时序配准算法的时间网络进行了对比分析。结果表明，相比NESD中的序贯网络以及MST-ESD中的最小生成树网络，利用高质量网络的BF-ESD算法具有更高的估计精度，不确定性相应减少。

虽然本文方法仅从时序TOPS模式数据配准给出解决方案，但是基于Bellman-Ford的时间网络能够在不改变算法的条件下延伸至小基线集的InSAR时序分析，从而改善用经验性阈值确定干涉子集的缺点。

致谢：Sentinel-1数据由ESA/Copernicus提供。