注重“真体验”，让学习在关键环节的真实经历中走向深刻——以《三角形的面积》教学为例

文|管小冬

“真体验”是指数学教学中，在发现问题、提出问题、解决问题、回顾反思等环节，教师注重引导学生像初始发现者（研究者）那样，经历、形成对问题解决原初而真实的体验。在汉语辞典中，“体验”一词有过程与结果两个维度的含义。即，体验既是一种行为过程，“亲身经历，实地领会”；又是这一行为过程的结果，“亲身实践所获得的经验”。现代课程论特别注重课程内涵的动态意义——“课程即体验”，认为“课程要提供一种充满情感、富有思考、感受多重的真实体验”。因为“真体验”能帮助学生不断积累数学学习与问题解决的“真经验”，并在此过程中发展数学思考，实现数学核心素养的不断提升，进而获得“适应未来社会工作、生活与学习的能力”，成长为“社会主义的建设者与接班人”。

情境数学之所以注重学生在数学学习过程中的“真体验”，是因为小学阶段的数学课程内容都是人类文明发展历程中，历经几百甚至是几千年探索出的智慧结晶。为使学生能在较短的时间内高效地掌握这些数学成果，教材在编排时，往往会选择性地省略数学知识形成所经历的初始想法、试误、反思、调整等思维过程，或是将数学知识以一种简明的逻辑结构直接呈现给学生，或是引导学生经由一条“捷径”直奔数学知识的最终形式。对此，北京师范大学郭华教授将之称为教学中的“第一次倒转”。同时，他又强调，教师的教学应在“承认‘第一次倒转’的基础上，充分考虑学生与知识的心理距离及学习感受，把第一次‘倒过来’的过程再‘倒回去’”，即让学生在亲历知识发现与建构的过程中形成数学学习与解决问题的“真体验”。

【案例】苏教版五年级上册《三角形的面积》

在《三角形的面积》一课教学中，教材直接给出下图，要求学生“想办法算出涂色三角形的面积”。

这样的设计，一是借助方格图引导学生进一步理解三角形面积的本质，即三角形的面积就是指其所包含的单位面积的多少；二是引导学生观察、发现图中三角形与平行四边形之间的关系，探究三角形面积的计算方法；三是引导学生进一步感悟数学研究中分类与归纳的思想，即通过对锐角三角形、直角三角形和钝角三角形这三类三角形面积计算方法的研究，可以归纳出三角形面积计算的一般方法。

然而，细细审视就会发现，这样的设计其实是从人类数学认识的“终点”出发，给出了一条学生直接学习“三角形面积计算方法”的“最佳路径”。在这条“最佳路径”上，学生走得平稳且几无波澜。因为他们基本无需经历形成初始想法、试误、反思、调整等曲折过程，就直接触碰到了人类对“三角形面积计算”研究的最高成果。

但我们知道，学生的数学学习，归根结底，是在掌握知识与技能的同时，获得数学核心素养的发展，以利于未来生活中真实而复杂的情境下的问题解决。如此，在学生奔向人类数学研究最高成果的道路上，最不能缺少的，恰恰应该是对数学知识发生发展过程中“关键环节”的“真体验”。因为，这些“真体验”是真正致力于帮助学生感悟数学的思想方法、积累数学的活动经验、培育数学的研究精神的。

基于以上思考，我对“三角形的面积”这部分内容的教学进行了重组与实践，现摘取其中两个片断，供大家参考。

片断一：立足已有经验，寻找解决问题的突破口。

课始，教师借助课件创设情境：王叔叔家正在装修，需要用到一些三角形的装饰板。（如下图）这种装饰板的售价是120元/平方米。使用这些装饰板一共需要多少元？

师：看到这个问题，大家有什么想法？

生：要求一共需要多少元，我们就要先知道这些三角形装饰板的面积是多少。

师：对。今天这节课我们就来研究三角形的面积。

师：上面这些三角形中，你想先研究哪个？

生：我想先研究第一个三角形，因为它是个直角三角形。我们知道，直角三角形是长方形的一半。

（其他学生纷纷表示赞同）

师：那怎样才能知道这个直角三角形的面积呢？需要用到哪些数据？请大家拿出作业纸，写一写、画一画，给出你的方案。

（学生独立研究，教师巡视指导，重点提醒学生理清三角形与长方形之间的关系。随后组织开展交流）

生：（展示自己的方案）大家看，这个直角三角形是它对应的长方形面积的一半。我们知道，长方形的面积=长×宽，而在这里，长方形的长和宽分别是这个直角三角形的两条直角边。所以，只要知道这个直角三角形的两条直角边的长度，就能算出长方形的面积，再除以2，得到的就是这个直角三角形的面积。

师：对于他的解决方案，大家是怎么想的？

（学生均表示同意）

师：如果是其他的直角三角形，这个方案也有用吗？

生：有用。

师：我想问问，在这个方案中，为什么大家会想到直角三角形对应的长方形？

生：因为长方形的面积计算方法我们已经学过了。

生：三年级时我们就知道了长方形的对角线可以把它分成两个一样的三角形。

师：大家能运用自己的已有知识和经验去思考，真棒！下面，我们就用这个方法，先量一量，再计算出这个直角三角形的面积。

上述片断中，教师在创设情境引出问题后，追问学生“上面这些三角形中，你想先研究哪个？”意在引导学生联系已有的知识与经验作出选择。而学生之所以会选择先研究直角三角形，是因为在他们的认知与经验系统中，对“直角三角形与对应长方形”图式的影像要远比“三角形与对应平行四边形”图式的更强烈，也更易被唤醒与提取。当然，学生的初始想法是感性的，甚至是模糊的。而落实于纸面的方案设计及随后的交流，正是意在引导他们通过深入的观察与对比，从感性经验走向理性思考，从直观认识走向理性分析。在这一过程的“真体验”中，学生会认识到：当遇到一个新问题时，可以先思考有哪些已有的知识或经验与这一问题的解决有联系或相似，从中可能会找到解决问题的突破口。

片断二：基于已有方案，持续推进问题解决。

师：剩下的两个三角形，都不是直角三角形，它们的面积又该怎样计算呢？刚才直角三角形面积的解决方案会对我们有帮助吗？这样，每人选择其中一个图形，在作业纸上试一试。

（学生先独立尝试，随后在四人小组中交流自己的方案或遇到的困难）

师：我们先来交流第二个图形——锐角三角形面积的解决方案。

生：一开始，我在想这个锐角三角形是不是也可以转化成长方形。但好像不行，因为它的三个角都是锐角。后来我就突然想到，它对应的应该是平行四边形，而平行四边形的面积我们也是会算的。大家看（图1），平行四边形的面积=底×高，而在图中，平行四边形和三角形的底和高是一致的，所以，我们可以用三角形的底乘高，算出平行四边形的面积，再除以2，就是这个锐角三角形的面积了。

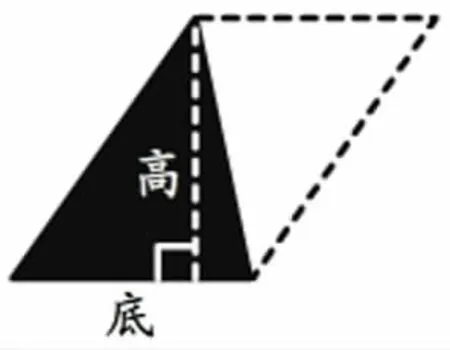
图1

生：我开始时也遇到了与他同样的困难，但在四人小组交流时受到了启发。大家看（图2），锐角三角形虽然不能直接转化成长方形，但可以沿一条高分成两个直角三角形，这样就可以用前面的方法算了。画好图后我又发现，不用分别算两个直角三角形的面积，因为锐角三角形的面积就是这个长方形面积的一半。

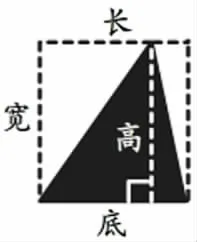
图2

师：仔细观察这两种方案，有联系吗？

生：从方案1到方案2，正好就是前面我们研究平行四边形面积计算时把平行四边形转化成长方形的那两幅图。

生：都是先用三角形的底乘高，算出对应的平行四边形或长方形的面积，再除以2，得到三角形的面积。

师：能把现在的研究与前面的学习及时联系，真棒。小结一下，与直角三角形一样，锐角三角形面积的计算方法也是底乘高除以2，不过这里的底乘高，既可以看作是它对应的长方形，也可以是它对应的平行四边形。

教学中，如果不像教材例题图那样给出明确的提示，学生是鲜少会想到用两个完全一样的三角形去拼成平行四边形的。这是因为，在此前有关图形面积的研究中，学生并未涉及这样的方法。上述片断中，教师对学生研究的不加指导与“放任”，正是意在让他们真实经历由初始想法走向问题解决过程中可能遇到的试误、反思、调整等关键环节。因为，对于真实的问题解决而言，研究不会一直一帆风顺。比获得最终方案或结论更重要的是，在遭遇困难时，学会坚持长时间思考，学会寻找可能的化解方法并积极尝试，学会与同伴交流，寻求启发与帮助。

“课程论之父”泰勒认为“教育的基本手段是提供学习经验”。杜威曾说：“一盎司经验胜过一吨理论。”立足于“真情境”基础上的“真体验”，正是意在突出：学生的学习，应立足基础知识与基本技能，又要超越基础知识与基本技能，注重在“关键环节”的“真体验”中积累“真经验”，形成“真情感”，进而感悟数学的思想与方法，体悟数学研究中的意志、品质与精神，实现对知识的深刻理解，对技能的深度掌握。