数形结合 构建模型
——《归一问题》教学思考与实践
2021-06-25於方婷
文|於方婷
《归一问题》是浙教版三年级上册的内容,是在学生学习了“每份数”“份数”“总数”三者之间关系的基础上进行教学的。这一内容从直观的天平图着手,让学生经历从直观图示中抽象出数量关系的过程,在不同情境中概括出共同的模型,初步感知归一问题的解决方法。
【教学过程】
一、借助天平直观,初步感知归一问题的基本结构
1.求包裹a有多重。
师:我们今天的学习从简单的天平开始。

师:每个小正方体一样重,包裹a有多重?
生:包裹a和三个小正方体一样重。
师:你能补充一个条件,帮助我们求出包裹a具体有多重吗?
生:如果知道一个小正方体有多重,就能求出包裹a具体有多重了。
师:那如果我补充的条件是这样的——你也能解答吗?(如下图)
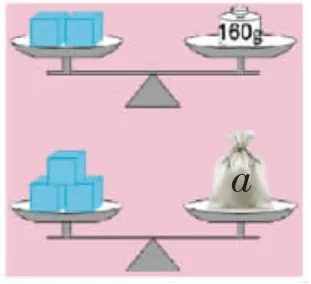
生:160÷2×3=240g。
师:你是怎么想的?
生:两个小正方体是160g,所以一个小正方体是160÷2=80g,包裹a相当于三个小正方体的质量,再乘以3就可以了。
生:也可以从下面的天平图开始想,包裹a和三个小正方体一样重,要先知道一个小正方体有多重,再根据上面的天平图可以求出一个小正方体的质量是160÷2=80g,乘以3求出三个小正方体的质量,就是包裹a的质量。
师:刚才这两种想法都是要先算什么?
生:都是先求出一个小正方体有多重。
师:哪个算式是先求一个小正方体有多重的?
生:160÷2。
【设计意图:在简单的天平图的引导下,通过“包裹a有多重?”“要求包裹a具体有多重,需要补充什么条件?”这两个问题,让学生明确要求包裹a具体有多重,需要知道一个小正方体表示多少,再乘以小正方体的个数就可以了。】
2.求包裹b有多重。
师:下面图中的每个小正方体也是一样重的,你知道包裹b有多重吗?

生:400÷5×4=320g。
师:你是怎么想的?
生:400÷5先求出一个小正方体的质量,再乘以4,求出四个小正方体的质量。
师:他先算什么?
生:一个小正方体有多重。
师:哪个算式是先求一个小正方体有多重的?
生:400÷5。
师:为什么要乘以4?
生:因为包裹b是四个小正方体那么重。
3.比较解题思路。
师:观察这两题的解题思路,它们有什么相同的地方?
生:都是先求出一个小正方体的质量,(板书)再求这样的几个小正方体的质量。
【设计意图:在直观图示的导引下,结合具体的解题经历,学生充分体会到,解决这两道题时,都是先解决“一个小正方体多重”的问题。通过对比归纳,突出“一个小正方体多重”这个“一份数”,初步感知归一问题的基本结构。】
二、利用图形直观,构建归一问题的模型
1.出示方格图。
师:要求下面整个图形表示多少,你能解决吗?

生:这题没有办法做,没有条件。
师:你觉得需要补充什么条件?
生:一个小正方形表示多少?
生:告诉我们涂色部分是多少也可以。
生:空白部分表示多少?
课件出示完整题目:涂色部分是150。求整个图形表示多少?
2.学生独立尝试。
3.指名汇报。
【设计意图:直接出示图片,引导学生补充条件,从直接想知道“一个正方形表示多少”逐步拓展到“涂色部分表示多少”“空白部分表示多少”,表明学生认识到可以从已知“一”扩展到主动来“归一”,虽然补充的条件不同,但都需要先求出每个正方形是多少,凸显出“一”的重要性和必要性。】
4.比较三个例题的解题思路。

数学信息2个重160g5个重400g5个表示150问题包裹a(3个多重)包裹b(4个多重)整个图形(18个表示多少)列式160÷2×3=240g400÷5×4=320g150÷5×18=540images/BZ_17_1525_349_1568_391.pngimages/BZ_17_1792_349_1835_391.pngimages/BZ_17_1545_480_1587_522.pngimages/BZ_17_1815_480_1857_522.pngimages/BZ_17_2064_352_2106_394.pngimages/BZ_17_2071_481_2112_523.png
师:仔细观察我们解决的这三道题目。你有什么发现吗?
生:都要先求出其中的一份是多少。
师:求出其中一份之后呢?
生:有这样的几份就乘以几,再乘以所求的份数。
小结:通过除法,我们求出一份是多少,再乘以份数,就能求出总数。
5.构建归一问题的模型Ⅰ。
师:那你能用一个算式来表示其中这种关系吗?
生:□÷△×○。
师:谁能看明白?
生:□÷△就相当于例1中的“160÷2”,求的是一个小正方体的重量,○指的是三个。
生:□÷△指的是总数除以份数,求的是其中的一份,○指新要求的份数。
小结:像这样先求其中一份是多少的,我们称为归一问题,可以用“□÷△×○”的运算结构来解决。
【设计意图:表格归纳,沟通天平图和几何直观图之间的联系,突出“归一”的思想,构建解决正归一问题的模型,并用图形算式□÷△×○表征模型。】
6.构建归一问题的模型Ⅱ。
师:回到格子图,如果要表示210,要画几个格子?
生:210÷(150÷5)=7(个)。
师:你是怎么想的?
生1:150÷5先求出一个小正方形表示30,再用210除以30,求出需要画7个格子。
师:第一步也是先求什么?
生2:先求一个小正方形表示多少。
生3:也可以说先求出其中一份是多少。
师:为什么现在要210除以这样一份的量?
生4:因为要画几个格子,就是要求210里面有几个30,所以要用210÷30。
师:那它是归一问题吗?
生5:我觉得它不是归一问题,前面的归一问题是先求出其中一份的量,再乘以份数,求总数,而这一题并不是。
生6:我觉得它是归一问题。归一的意思是要先求其中的一份,它也是先求出其中一份的量,所以它也是归一问题,只是它和前面的不一样,前面的是已知份数,求总数;现在是已知总数,求份数。
师:我同意生6的意见。这个题目也是先求出其中的一份是多少,所以它也是归一问题。它可以用□÷△×○这样的结构来表示吗?
生:不能。
师:那可以怎样修改?
生7:☆÷(□÷△)。
小结:归一问题可以用□÷△×○或者☆÷(□÷△)两种图形算式来解决,它们都是先求出其中的一份,第Ⅰ种结构是已知份数求总数,第Ⅱ种结构是已知总数求份数。
【设计意图:在学生初步建立正归一的直观模型基础上,通过几何直观提出反归一的问题,在正反归一问题的比较中,进一步突出归一的基本特征,并且构建反归一问题的模型,用图形算式☆÷(□÷△)来表示。】
三、结合生活情境,沟通图形、具体数量之间的关系
1.寻找生活中的归一问题。
师:我们已经解决了图形中的归一问题,其实在我们的生活中也有许多归一问题。
要求:独立列式计算。完成后思考:这是归一问题吗?请说说你的理由。
(1)下图的杯子内已注入600毫升水,还要注入多少毫升水才能到达顶格?

(2)做蛋糕时放面粉和鸡蛋是有讲究的。一般来说,4个鸡蛋搭配100克面粉口感最好,按照这样的配方,500克面粉应搭配多少个鸡蛋?
2.学生完成后,分小组交流。
师:同学们基本已经完成,现在请四人小组内部讨论一下,每人选一题说一说你所列算式的意思,并且说一说它是归一问题吗?为什么?
3.集体交流第(1)题。
生:600÷5×3=360(毫升),600÷5先求出一小格是120毫升,再求出三格是360毫升。这里先求出其中一格是120毫升,所以这是归一问题。
4.集体交流第(2)题。
方法一:500÷(100÷4)=20(个)。
方法二:500÷100×4=20(个)。
小结:方法一是用归一的思路解决的,先求出其中的1个鸡蛋需要搭配25克面粉;方法二是把100克看成一份,500里有几个100就需要几个4,也是好办法。
【设计意图:解决同一问题有不同的方法,可以用反归一或倍比方法求解。在对比反归一和倍比方法时,学生能深化“一份数”的认识,这是对归一内涵的拓展。】
四、课堂小结
师:今天我们学习了什么?
生:我们今天学习了归一问题,可以用□÷△×○或者☆÷(□÷△)两种图形算式来解决。
师:那你能自己编一编题目吗?可以是用□÷△×○这样的结构解决,也可以是用☆÷(□÷△)这样的结构解决的。
生:我有320元,2个皮球需要160元,我可以买几个这样的皮球?
生:李师傅2小时能加工60个零件,8小时能加工多少个零件?
【设计意图:放手让学生自主编写归一问题,在对基本的数学模型进行各种情境变式的过程中,进一步把握基本结构,感受数学的特点和价值。】
