基于小波神经网络对铁路客运量的预测研究
2021-06-24唐琴琴
张 鹏,唐琴琴
(太原工业学院理学系,山西太原 030008)
铁路客运是我们生活中必不可少的一部分,预测研究铁路客运量是很有必要的,首先,我国资源丰富,但分布不均衡,而铁路客运这种交通方式不仅便捷,而且效率高;其次,近年来,人们在衣食住行方面的要求越来越高,需要对铁路客运进行准确地预测;最后,如果对铁路客运预测的不准确,这将导致决策者的方案失效,不利于铁路客运的发展,因此需要对铁路客运做出准确的预测。
主要研究小波神经网络模型,并预测铁路客运量。首先,将统计年鉴中的数据分为训练样本以及预测样本;其次,针对数据进行去噪处理是为了提升序列的光滑度,通过相空间重构[1]确定神经网络的输入层节点数,根据经验公式以及对比仿真实验确定隐含层节点数,隐含层函数选取小波基函数;最后,利用预测样本得到的结果与原始数据对比[2]。
1 小波神经网络
1.1 小波去噪
小波去噪是在原始信号的基础上,完成对原信号s(t)与噪声信号n(t)的区分,

其中n(t)服从的分布为正态分布n(t)~N(0,σ2)。
小波阈值除噪,起初需要指定一个界限值λ,该值也称为阈值,对阈值来说,能够将其划分为整体界限值以及部分界限值。进行小波变换以后,会得到小波分解系数wj,k,如果临界值大于小波系数,认为此系数因噪声形成,可将其删除;如果大于λ,可把原因归咎于信号,可引用此部分,进行重新构造得到结果。
1.2 相空间重构技术理论
相空间重构有两个关键的参数:嵌入维数m 和延迟时间τ,C -C 平均法对τ,w 的选取更可靠。设时间序列x={xi|i=1,2,…,N |}重构后,有新的序列X=,记X={Xi},为相空间中的点。嵌入时间序列关联积分表示相空间中任意两点之间距离小于r的概率:
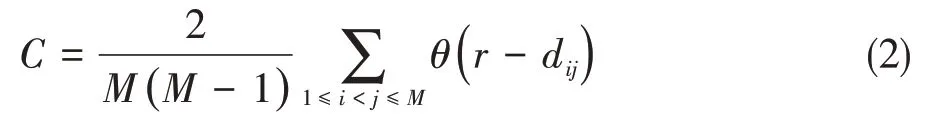
其中dij=‖ xi-xj‖(∞)表示点与点之间距离为矢量之差的无穷范数,θ(·)为Heaviside函数。检验统计量:S1(m,N,r,t)=C(m,N,r,t)-Cm(1,N,r,t),定义差量为:


1.3 神经网络原理
神经网络由输入层,隐含层和输出层组成。层与层之间权值不相同,通过信号的正向传递与误差的反向传递[3]实现,设输入层为xi,隐含层为yj,输出层为zl,实际输出为tl,第i输入层与第j隐含层之间权值为wij,第j 隐含层与第l 输出层之间权值为vjl,θj为隐含层的阈值,θl为输出层的阈值。
第j隐含层值为:
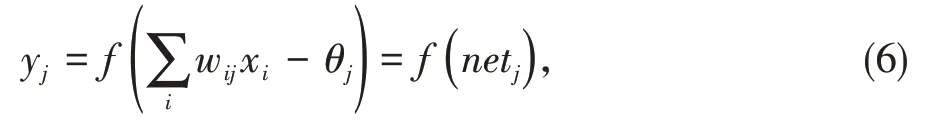
第l输出层值为:

输出层与实际值的误差:
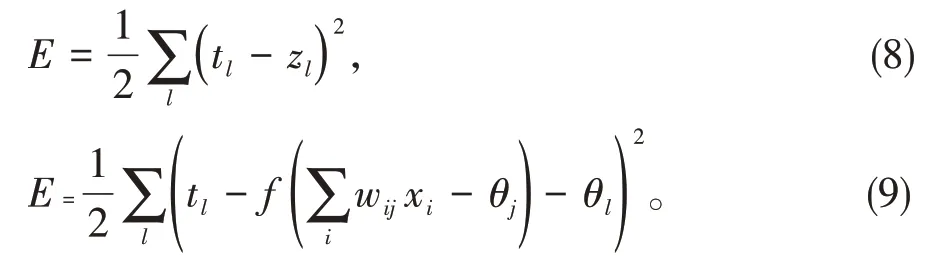
1.4 数据预处理
在对原始数据进行统计分析时,通常情况下,需要处理原始数据,对数据进行归一化[4]处理:

输出时对数据进行反归一化处理:
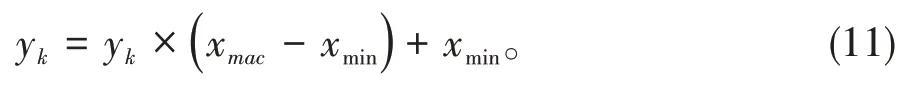
1.5 小波神经网络模型的构造
构造小波神经网络[5]时,隐含层函数需要采用小波基函数,根据经验,选择收敛的,区间内是单调递增的函数[6],平移因子,伸缩因子代替层与层之间的权值以及阈值。
网络输入为x1,x2,…,xn,输出为yi,小波神经网络层与层之间权值分别为wij,wjl,输入信号为xi(1,2,…,k),隐含层节点数由经验公式求得。
2 实证分析
2.1 提取实验数据
选取自国家统计局的铁路客运量月度数据,如图1所示。可知,原始数据有指数趋势[5],且具有周期性,取前150个数据为训练集,剩下的为预测集,对数据进行拟合以及预测。
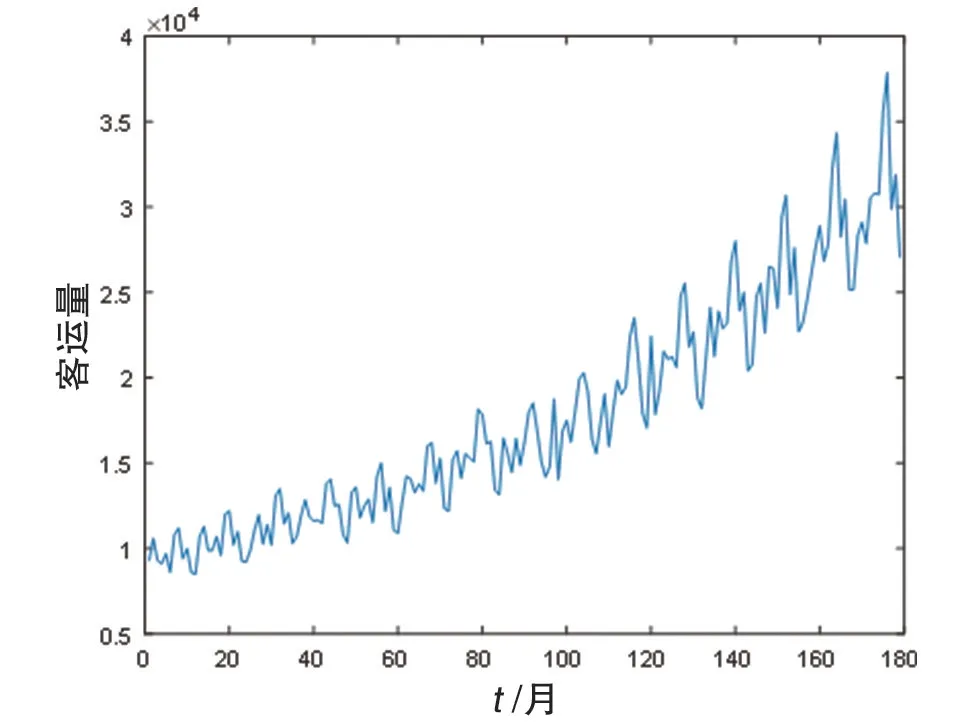
图1 原始数据图像
2.2 小波去噪
首先对数据进行去噪处理,原始时间序列可以小波分解为:

如图2为去噪后的信号:
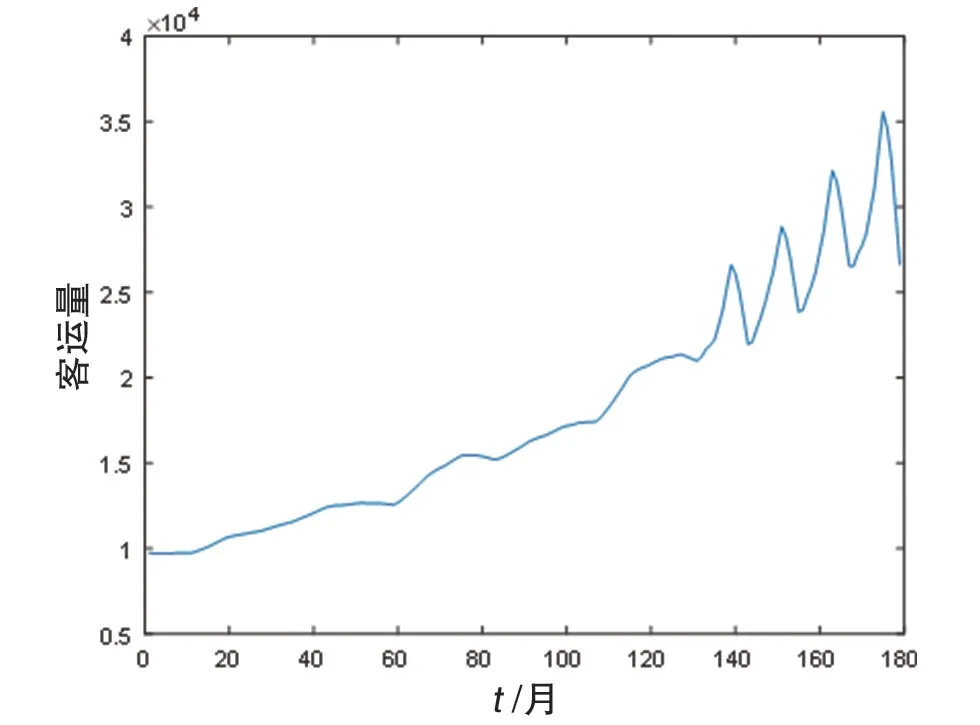
图2 去噪后数据
选择小波基函数为db6,分解层数为3。对原始数据进行去噪,去除噪声系数,去噪后图像相较于原始数据来说是光滑的,更有利于处理数据。
2.3 输入层节点数的确定
利用相空间重构处理去趋势数据,可以得出时间延迟为4,时间窗为3,因此嵌入维数为2,即小波神经网络的输入层节点数为2,将重构后的数据代入模型。
去趋势处理后的数据只含有周期性因素,没有指数趋势,有利于对原始数据相空间重构,求取时间延迟与时间窗,由图3 可得输入层的各个参数,将重构后的数据代入模型。
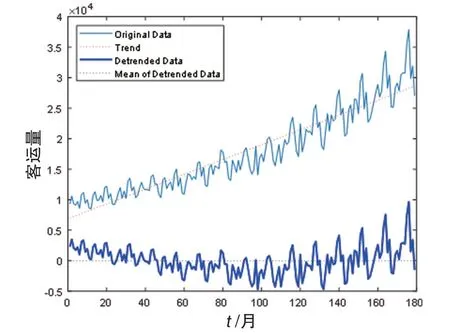
图3 去趋势处理
取时间延迟的范围为1~50,如图4为时间延迟以及时间窗图像。
图4 在t 为4 时取极小值点,因此取图像的极小值点4,即为延迟时间。图5 在t为3 时,取最小值,图像的最小值对应时间为时间窗,时间窗为3。
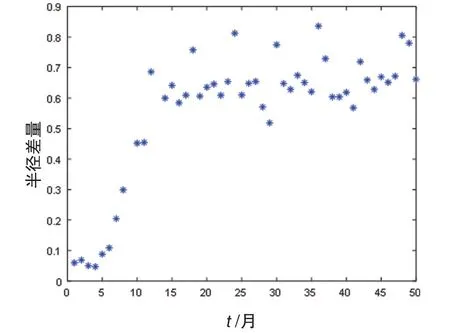
图4 时间延迟
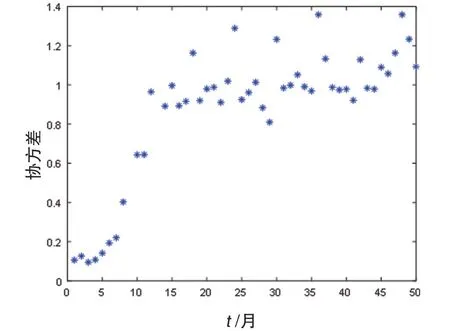
图5 时间窗
2.4 隐含层节点数的确定
通过对比仿真实验来确定小波神经网络的隐含层节点数,由经验公式可得:

a 为的常数,M,N 分别为输入层,输出层的节点数.通过仿真对比实验,隐含层数定为7。
2.5 对铁路客运量的预测研究
2.5.1 对原始数据分析
由相空间重构可得,输入层节点数为2,隐含层节点数为7,取隐含层函数为帽函数[7]的时候,网络模型最佳,可得到原始数据的训练集与其拟合值的对比图像以及预测集对比图像,如图6所示。
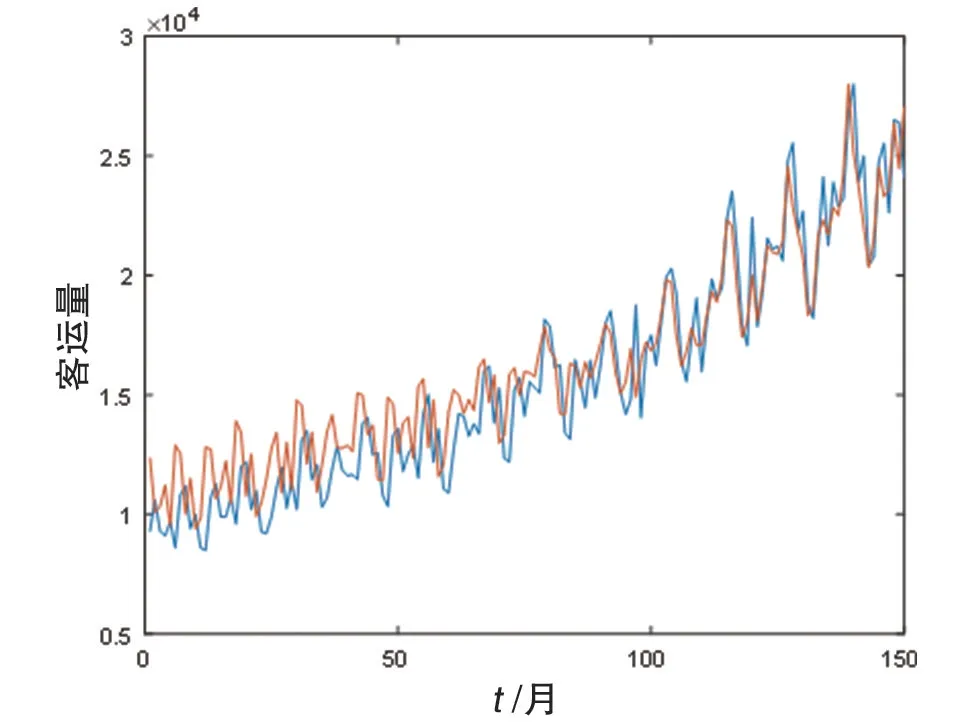
图6 原始数据与拟合值对比图
由图7 可知,误差相对很大,尤其是预测样本数据的波动性很大,所以预测效果不乐观。如图7所示为原始数据的每一个值与拟合值得到的误差图像,预测效果误差很大,其原因与原始数据的不光滑有关。
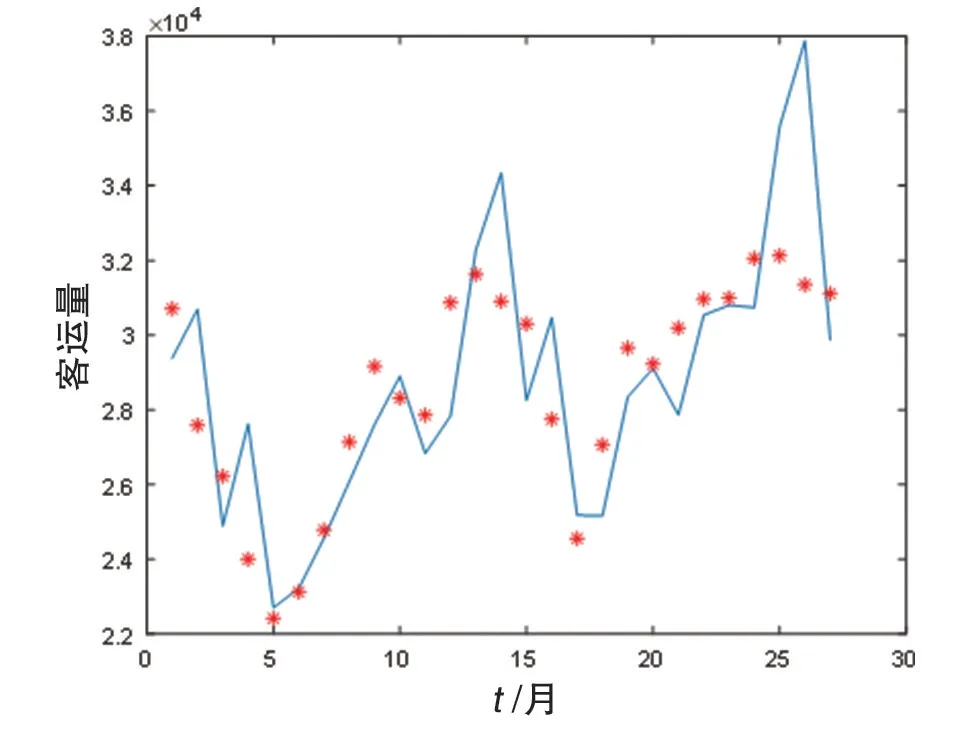
图7 预测值图像
2.5.2 小波去噪后分析
当进行小波去噪后,建立网络模型,如图8 所示为去噪后的数据与拟合值的对比图像以及预测集实际值与拟合值图像。
由图8可知,原始数据去噪后,数据较为光滑,拟合值几乎和原始数据去噪后的数据完全重合,网络模型误差小。对预测样本进行预测时,大部分点几乎是重合的,因此对原始数据进行去噪处理后,小波神经网络模拟效果较好。
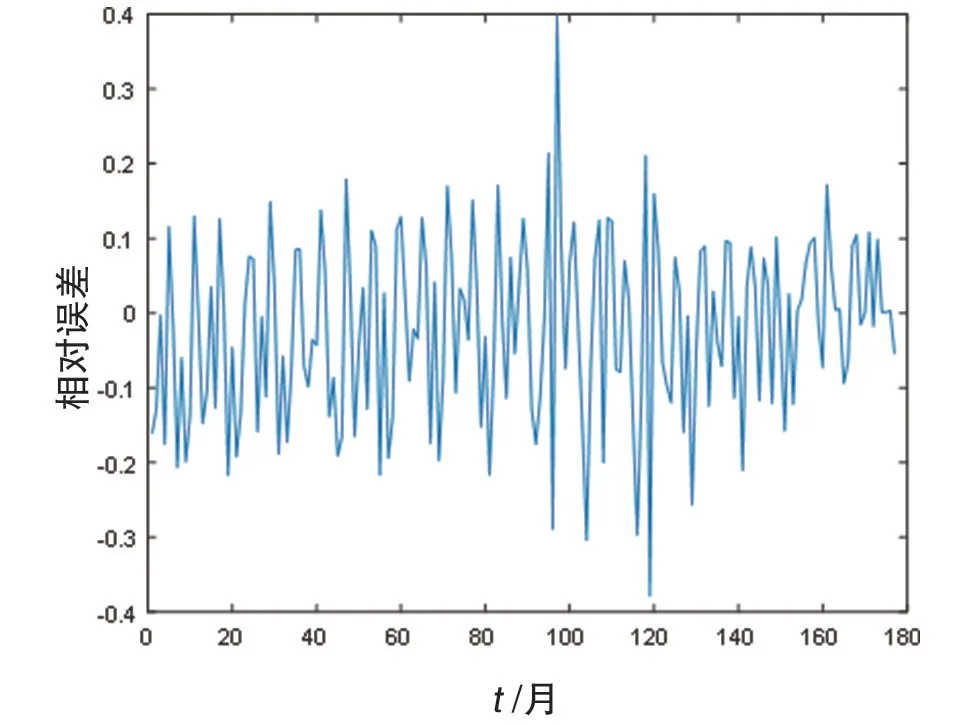
图8 神经网络误差图
如图9所示为每个点的误差图像,与未去噪的相比,误差很小。
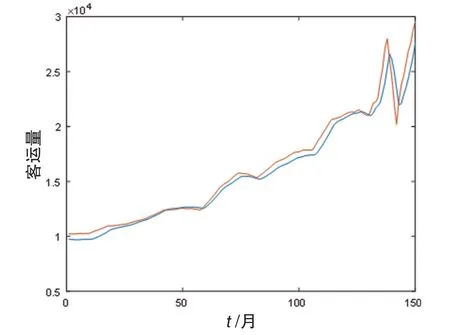
图9 去噪后数据与拟合值图像
由图9~11可知,对原始数据进行去噪后,预测集的实际值与小波神经网络的拟合值误差相对很小,预测效果好。
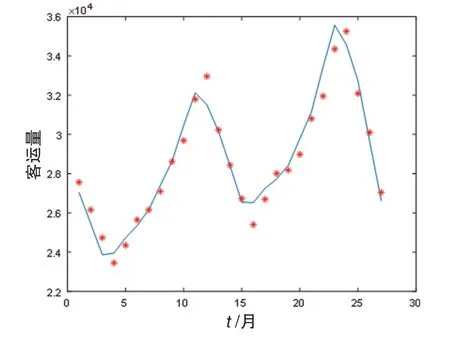
图10 预测实际值与拟合值图像
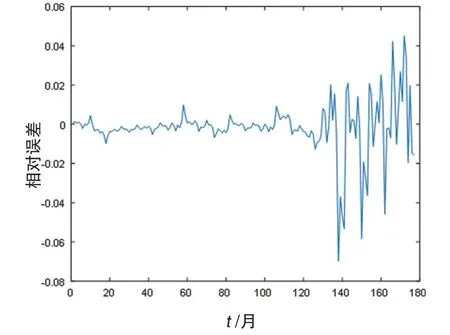
图11 预测实际值与拟合值误差
3 结论
利用小波神经网络对铁路客运量进行了预测研究,首先,对原始一维数据进行相空间重构,得到二维数据,其次计算隐含层节点数,最后进行小波神经网络的构建,隐含层函数选取小波函数,层与层之间的权值随机设定,将原始数据与去噪后的数据的实际值,拟合值作比较,去噪后的效果更好,但本论文数据量不大,因此需要扩大样本容量,会使网络模型更好.对小波函数的选择可利用数值法求解,如若用对比仿真实验,虽然简单,但模拟量较大。
