基于遗传算法优化模糊神经网络的温室温度预测模型

2021-06-24贾兰芳

山西大同大学学报(自然科学版) 2021年3期

张龙，贾兰芳

（长治学院电子信息与物理系，山西长治 046011）

我国作为农业生产大国，温室面积位居世界首位。预测是控制研究方面的前提，对研究温室内各种相互影响的环境因素具有重要指导意义[1-2]。但因温室系统自身具有很强的复杂性，温室内存在的环境因素又相互影响，所以温室系统的模型建立存在很大的难度[3]。为了进一步提高预测精度，许多学者提出了各种预测方法。崔丽珍[4]等对支持向量机进行了改进，构建了温室大棚温度预测模型；杨雷等[5]在温室大棚温度预测研究中，提出了基于PCA-PSO-LSSVM 模型；徐宇等[6]在智能温室温度预测研究中，提出了基于复数神经网络模型。针对温室温度与其他各种环境因素具有很高的耦合度，难以预测，文章建立一种基于遗传算法优化模糊神经网络温室温度预测模型，从而为精准调控奠定坚实的基础。

1 模型建立

1.1 模糊神经网络

该模型如图1 为五层结构[7-8]，依次为模糊输入层、模糊化层、模糊条件层、模糊判决层和去模糊化输出层。假设模糊系统只有两个输入变量分别为x1、x2，一个输出变量为y，每个输入变量在其论域上划分为两个模糊子集。

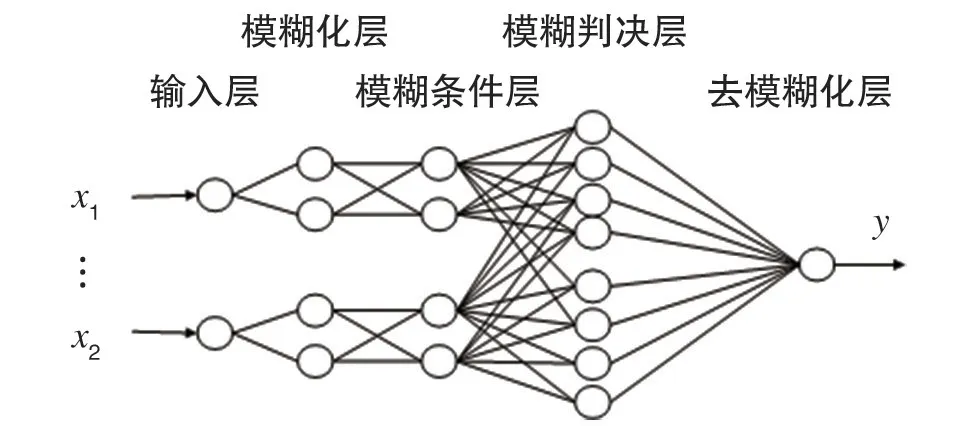
图1 模糊神经网络结构图

第2层：将输入层的输入变量通过一个或多个隶属函数模糊化，

第3层：针对的是模糊规则中的条件部分，对节点进行组合配合，实现各个输入模糊值的“乘”运算，

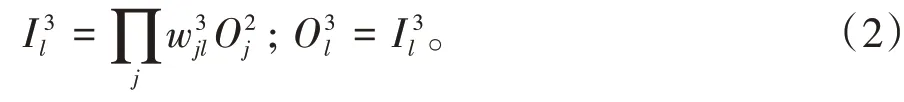
第4层：得出相应输出节点模糊值的大小，

第5层：本层节点的作用是“去模糊化”。将输出的模糊值形式还原为乘数值的形式，

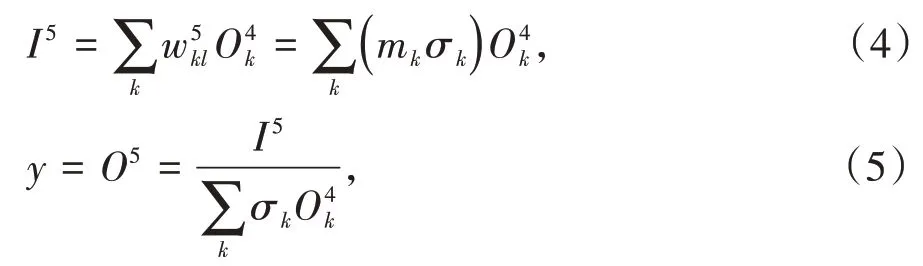
1.2 GA-FNN预测模型

采用的遗传算法（GA）[9]优化模糊神经网络（FNN）预测模型，模型内的隐含层节点数、隶属度函数参数值，即是网络中间层数、隶属函数的中心和宽度。图2为算法流程图。

图2 算法流程图

对输入样本数据做归一化处理，尽量减少因数据的量纲不同而造成的影响。即将实测数据通过归一化mapminmax 函数转换为[-1,1]的值。归一化mapminmax函数公式如下：

式中，xmax、xmin分别表示输入量的最小值和最大值，ymin、ymax为-1 和1，x为输入量的数据，y为归一化后输出数据；

设置网络初始化参数，隐含层节点数为15，隶属度函数参数Cji=0.01，bi=0.02。种群大小N=20，进化次数最大为100 次。选交叉概率为0.8，变异概率为0.1。

2 测试

2.1 数据来源

利用智能传感器采集某温室近7 d 的连续实际测量数据，样本数据包括室内温度、湿度、CO2、大气压和光照强度，后4 项数据作为输入数据，温度数据作为输出数据。每隔2 min采集一次，共采集了4 720组样本数据，前4 320 组样本数据作为训练，最后400组样本数据作为输出测试，10 min后的温度数据为预测输出数据。表1为采集的部分样本数据。

表1 部分样本数据

2.2 评价指标

为了验证模型性能，分别采用均方根误差（RMSE）、平均绝对误差（MAE）和平均绝对百分误差(MAPE)对预测模型作评价分析，具体计算公式如下：

式中，VRMSE表示均方根误差，VMAE表示平均绝度误差，VMAPE表示平均绝对百分误差，yi表示真实值，表示预测值，N是测试样本中的数量。

2.3 仿真结果与分析

将数据输入预测模型，通过MATLAB 软件对该模型与未优化的模糊神经网络模型进行验证，获得最佳隐含层节点数为4、隶属度函数参数（Cji，b）i参数分别为2.920 3和2.258 8。

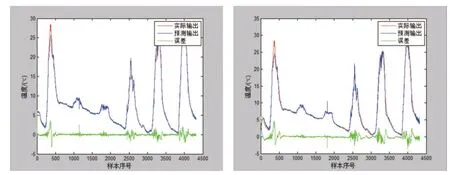
图3 GA-FNN与FNN训练效果对比图

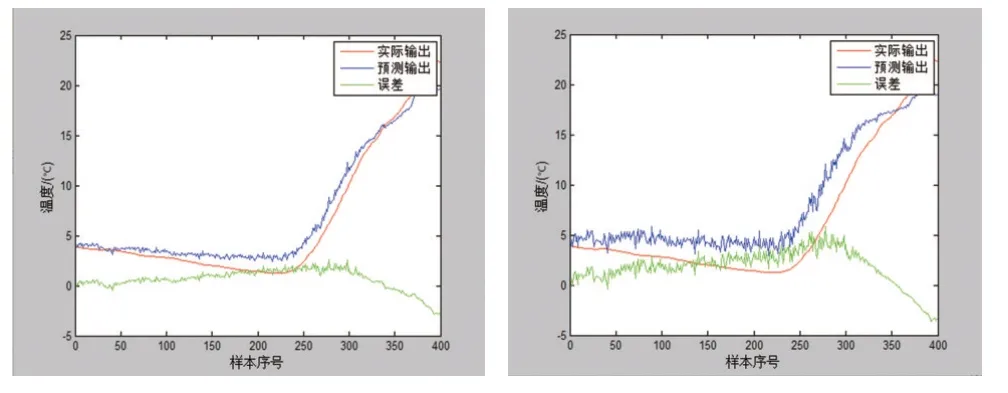
图4 GA-FNN与FNN预测效果对比图

运算结果对比如表2 所示。从表2 中可以看出，模糊神经网络预测（FNN）模型的RMSE 为2.528 5，MAE 为2.253 5，MAPE 为7.488 1，经过遗传算法优化的模糊神经网络预测（GA-FNN）模型的RMSE 为1.213 1，MAE 为1.030 6，MAPE 为6.207 1，分别提升了51.3%，54.2%，17.1%。