基于谱数据构造的子周期Jacobi矩阵*

郭雪娟， 吉雁斐

(中北大学 理学院， 山西 太原 030051)

0 引 言

周期Jacobi矩阵形式如下

其中，αi∈R，βi>0,](i=1,2,…,n).周期Jacobi矩阵来源于周期Toda lattices和连分数的应用[1-2]， 它的逆特征值问题主要出现在逆散射问题中， 具有十分重要的实际意义， Boley 和Golub在文献[3-4]和Ferguson在文献[5]中分别对此问题进行了相关研究.

本文对此类矩阵进行推广， 研究以下形式的子周期Jacobi矩阵逆特征值问题[6-7]

(1)

记矩阵X的谱为σ(X)， 对于式(1)中的矩阵Sn， 规定

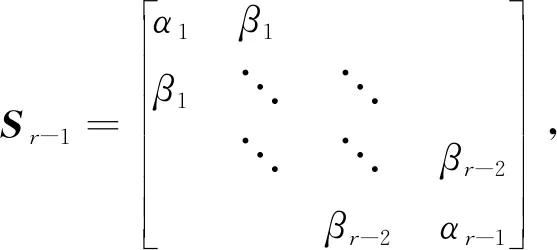
(2)

问题：给定一个正数β以及三个集合λ={λ1,λ2,…,λn}⊂C，μ(1)={μ1,μ2,…,μr}⊂R，μ(2)={μr+1,μr+2,…,μn-1}⊂R， 3≤r≤n， 其中λ在复共轭下是封闭的， 且满足

λ1<μ1<λ2<…<λn-1<μn-1<λn.

(3)

求一个子周期Jacobi矩阵Sn使得

(4)

上述问题简称SPJIEP.

引理1[8]已知Jm是一个m阶Jacobi矩阵且其次对角元为γ1,γ2,…,γm-1， 令si是特征值ξi对应的单位特征向量，i=1,2,…,m， 则

χ′(ξi)s1ism,i=γ1γ2…γm-1,i=1,2,…,m，

其中,χ′(ξ)是χ(ξ)=det(ξIm-Jm)的导数且s1i和sm,i分别是si的第一个和最后一个分量.

引理2[9]已知{ξ1,ξ2,…,ξm}是一组在复共轭下是封闭的复数， {η1,η2,…,ηm-1}是一组成对且互不相同的实数， 且ηi∉{ξ1,ξ2,…,ξm}， 则线性代数方程组

i=1,2,…,m.

1 子周期Jacobi矩阵的谱性质

因为Sr-1和Sr+1,n都是Jacobi矩阵， 所以这两个矩阵均有实的且互异的特征值. 因此， 考虑

σ(Sn)=λ,λ={λ1,λ2,…,λn},

σ(Sr-1)=μ(1),μ(1)={μ1,μ2,…,μr-1},

(5)

σ(Sr+1,n)=μ(2),μ(2)={μr,μr+1,…,μn-1},

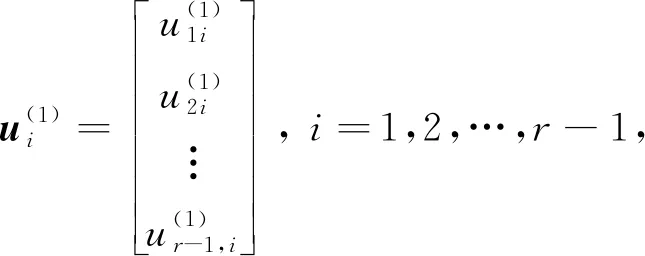
引理3[6]令N1={1,2,…,r-1}， N2={r,r+1,…,n-1}，μ(1)和μ(2)如式(5)所示， 则：

2) 当且仅当μj∈μ(1)∩μ(2)时，μj∈σ(Sn),j∈N2.

引理4[6]若μ(1)∩μ(2)=∅， 且存在一个集合I={i1,i2,…,is}∈N1， 使得

则μi1,μi2,…,μis是Sn的特征值，Sn其余的特征值是有理函数

(6)

的n-s个零点.

注1上述定理中的集合I可以为空集， 此时Sn的特征值即为式(2)的n个零解.

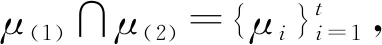
j∈(SI1)∪((N1S)I2),

则μj,j∈I1∪I2也是Sn的特征值， 其余特征值是有理函数

(7)

的n-t-s2个零点.

注2上述定理中的集合I1或I2均可以为空集， 此时Sn的特征值可由式(7)类似得到.

定理1当μ(1)∩μ(2)=∅时， 取I={1,2,…,s}， 令λi=μi,i∈I， 将μi,i∈(N1∪N2)I升序排列， 则不等式(8)成立.

λs+1<μs+1<λs+2<…<λn-1<μn-1<λn,

(8)

λt+s2+1<μt+s2+1<λt+s2+2<…<μn-1<λn.

(9)

证明1)μ(1)∩μ(2)=∅，Sn的特征值满足式(6)， 即F1(λ)=0.将F1(λ)写作

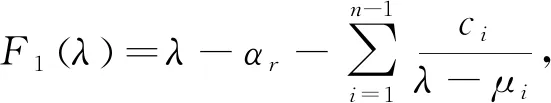
其中，ci>0,i=1,2,…,n-1.对于一个充分小的正数ε，

F1(μi-ε)>0，

F1(μi+ε)<0，i=1,2,…,n-1，

F1(-∞)<0，F1(+∞)>0，

因此，λs+1<μs+1<λs+2<…<λn-1<μn-1<λn成立.

其中，ci>0,i=1,2,…,n-1， 且F2(λ)的极点为μ1,μ2,…,μt,μt+s2+1,μt+s2+2,…,μr-1,μr+t,…,μn-1， 已知μi,i∈S={1,2,…,t}和μj,j∈I1∪I2均为Sn的特征值， 不妨设λi=μi,i=1,2,…,t，λi=μi,i=t+1,t+2,…,t+s2， 则Sn剩余的特征值为F2(λ)的零点， 即λt+s2+1,λt+s2+2,…,λn.又由于μi=μi+r+1,i=1,2,…,t， 则F2(λ)的极点为μt+s2+1,μt+s2+2,…,μr-1,μr,μr+1,…,μr+t+1,…,μn-1， 故类似μ(1)∩μ(2)=∅的情况可知，F2(λ)的零点与极点也存在交错关系， 即λt+s2+1<μt+s2+1<λt+s2+2<…<μn-1<λn.

2 SPJIEP有解的充要条件

对于如SPJIEP所示的λ，μ(1)和μ(2)， 本节按照

μ(1)∩μ(2)=∅和μ(1)∩μ(2)≠∅

两种情形讨论SPJIEP的可解性.

2.1 考虑μ(1)∩μ(2)=∅的情况

不失一般性， 考虑正整数集合I={1,2,…,s}， 且定义

j=s+1,s+2,…,n-1.

(10)

定理2对于如SPJIEP所示的正数β， 集合λ，μ(1)和μ(2).假设μ(1)∩μ(2)=∅， I={1,2,…,s}⊂N1，λi=μi，i∈I， 且满足不等式λs+1<μs+1<λs+2<…<λn-1<μn-1<λn.集合xj,j=s+1,s+2,…,n-1如式(10)所示.当且仅当满足下列条件时SPJIEP有解且有2r-s-1个不同的解：

证明必要性：假定存在一个形如式(1)的子周期Jacobi矩阵Sn使得式(4)成立. 由引理1可得

(11)

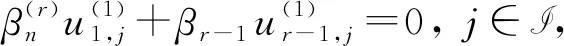
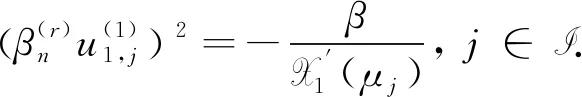
(12)

(13)

由式(12)， 式(13)可知条件2)成立.

充分性：假定条件1)和2)成立， 考虑非零实数xj,j=s+1,s+2,…,n-1如式(10)所示， 定义

(14)

(15)

(16)

(17)

(18)

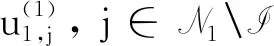
注3上述定理中I可以为空集， 此时SPJIEP有解的充要条件可由定理2类似得到， 且最多有2r-1个不同的解.

2.2 考虑μ(1)∩μ(2)≠∅的情况

考虑正整数集合I1={1,2,…,s1}， I2={t+1,t+2,…,t+s2}， 且定义

j=t+s2+1,t+s2+2,…,n-1.

(19)

1) 存在任意实数θj∉{0,1}， 使得θjxr-1+j>0, (1-θj)xr-1+j>0,j∈SI1；

证明必要性： 可由定理2中必要性的证明类似得到.

充分性：假定条件1)～4)均成立， 考虑非零实数xj,j=t+s2+1,t+s2+2,…,n-1如式(19)所示， 定义

(20)

(22)

(23)

由于θj∉{0,1}是任意的， 所以满足上述所有条件可以得到无穷多个解.

注4上述定理中I1, I2均可以为空集， 此时SPJIEP有解的充要条件可由定理3类似得到， 且均有无穷多解.

推论1对于如SPJIEP所示的正数β， 集合λ，μ(1)和μ(2)， 假设μ(1)∩μ(2)=∅， I={1,2,…,s}⊂N1，λi=μi，i∈I， 且满足λs+1<μs+1<λs+2<…<λn-1<μn-1<λn.集合xj,j∈(N1∪N2)I如式(10)所示.当且仅当满足下列条件时SPJIEP有唯一解：

2) 定理2中的条件2)成立；

其中I为空集时SPJIEP有唯一解的充要条件可由推论1类似得到.

3 构造子周期Jacobi矩阵的数值算法及实例验证

下面将建立构造子周期Jacobi矩阵Sn的算法.

算法 1SPJIEP的解

输入： 如SPJIEP中所示的β,λ,μ(1),μ(2)

输出：Sn.

1) 若μ(1)∩μ(2)=∅， 则接步骤2)， 否则接步骤4)；

2) 由式(10)计算xj,j∈(N1∪N2)I；

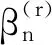
5) 由式(19)计算xj,j=t+s2+1,t+s2+2,…,n-1， 并在R{0,1}中选择θj∉{0,1},j∈(SI1)；

8) 如果满足定理2中的条件4)～5)， 则可通过向前的Lanczos算法分别结合(I1,μ(1),g1)和(I2,μ(2),g2)重构矩阵Sr-1和Sr+1,n， 否则该问题无解；

10) 输出Sn， 结束.

例1令n=7,r=4， 给定正数β=1和集合λ,μ(1),μ(2)， 如表1 所示.

表1 谱数据λ={λ1,λ2,…,λ7}, μ(1)={μ1,μ2,μ3},μ(2)={μ4,μ5,μ6}

显然μ(1)∩μ(2)=∅且I=∅， 由算法1可得

x1=0.439 198 451 967 014,

x2=0.475 249 790 525 101,

x3=1.085 551 757 507 88,

x4=0.989 147 543 776 782,

x5=1.748 293 216 267 16,

x6=1.262 559 239 956 07,

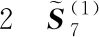
表的主对角元与次对角元

表3 输入的谱数据λ,μ(1),μ(2)和输出的谱数据对比结果

4 结 论

本文共分μ(1)∩μ(2)=∅和μ(1)∩μ(2)≠∅两种情况依次讨论了子周期Jacobi矩阵的逆特征值问题. 首先得到了关于λ， μ(1)和μ(2)的交错不等式，其次， 在建立算法去构造子周期Jacobi矩阵的过程中， 由于中的符号“+”或“-”都可取， 因此， 我们构造出了8个不同的且均满足SPJIEP有解的充要条件的矩阵， 实例仿真表明构造出的8个矩阵的谱数据与给定的谱数据误差极小， 验证了本文所给算法的有效性.