山西省新型冠状病毒疫情分析及防控措施评估*
2021-06-24张晓琴荆文君
张晓琴, 李 宇, 荆文君
(山西财经大学 统计学院, 山西 太原 030006)
新型冠状病毒肺炎在全球爆发, 截止2020年11月, 全球COVID-19累计确诊人数已达上千万, 其中几百万人患病死亡, 可见病毒对人类生命健康威胁之大, 有效预防和控制疫情成为当前最受关注的问题之一. 研究疫情发展规律、 评估防控措施, 对有效控制疫情传播、 助力全球经济发展具有重要意义.
传染病动力学模型通过建立基本假设、 设置参数与变量描述疾病发展过程和传播规律, 能科学预测疾病流行趋势、 评估防控效果[1]. 目前, 大量学者应用传染病动力学模型对COVID-19展开研究. 范如国等[2]基于复杂网络建立SEIR模型, 给出3种不同潜伏期下参数仿真分析与疫情拐点预测. 王霞等[3]对SEIR模型进行改进, 将 2019年同期人口流动网络与之结合, 重点分析武汉及周边地区的复工时间节点. 李倩等[4]建立传染病数学模型刻画COVID-19疫情期间隔离措施实施作用, 认为滞后确诊增大了感染规模. 赵序茅[5]基于百度地图大数据, 认为武汉输出人口与全国各地确诊人数在疫情初期呈正相关. 周涛等[6]基于SEIR模型对基本再生数进行估计, 认为COVID-19传播能力略高于SARS. 张庆等[7]利用传染病模型中的基本再生数对山西省与其他地区的疫情做了对比分析. 离散化的差分方程模型在传染病研究上使用也越来越多, 刘双等[8]通过建立具有时滞效应的差分方程来研究北京SARS疫情, 对改变收治速度时疫情发展的状况进行了模拟分析. 李浩等[9]建立具有时滞和非线性发生率的离散SIRS模型, 对差分方程解的性质给予证明. 此外, 还有学者对太原市COVID-19病毒在不同情境下的传播做了仿真模拟, 对疫情的防控给予了很大支持[10].
无症状感染者由于没有明显症状又存在传染性, 容易造成聚集性传染, 给疫情防控带来巨大挑战[11]. 湖南郴州一个家庭6天内出现4例确诊和1例无症状, 调查发现无症状感染者是传染源[12]. 随后, 中国多地陆续发现无症状感染者及其传播事件. 随着人们对COVID-19认识加深, 无症状感染者也受到有关部门重视, 学者们也对此类人群展开研究. 孙皓宸等[13]考虑无症状患者对校园疫情的影响, 认为无症状患者越多病毒传播越快.
鉴于此, 本文考虑潜伏者与无症状感染者均具有传染性、 防控治疗等具有时滞性, 构建一类离散化的差分方程模型, 对山西省疫情发展状况、 无症状感染者的影响, 以及防控措施效果进行研究, 为科学认识COVID-19传播模式提供理论参考.
1 数据与模型说明
1.1 数据来源
自疫情爆发以来, 山西省卫健委每日公布COVID-19数据, 包括新增确诊数、 累计确诊数、 新增治愈和累计治愈数等. 从疫情数据可知: 山西省在2020年1月22日出现第一例病例, 3月13日所有确诊患者治愈出院; 3月23日开始出现境外输入病例, 由于境外输入人员被全部隔离, 因此不在本文研究范围内.
本文针对1月22日到3月13日的数据, 建立差分方程模型来模拟疫情发展, 并预测3月14日到3月22日疫情发展, 通过与实际情况对比来验证模型的有效性. 表1 是山西省疫情原始数据.
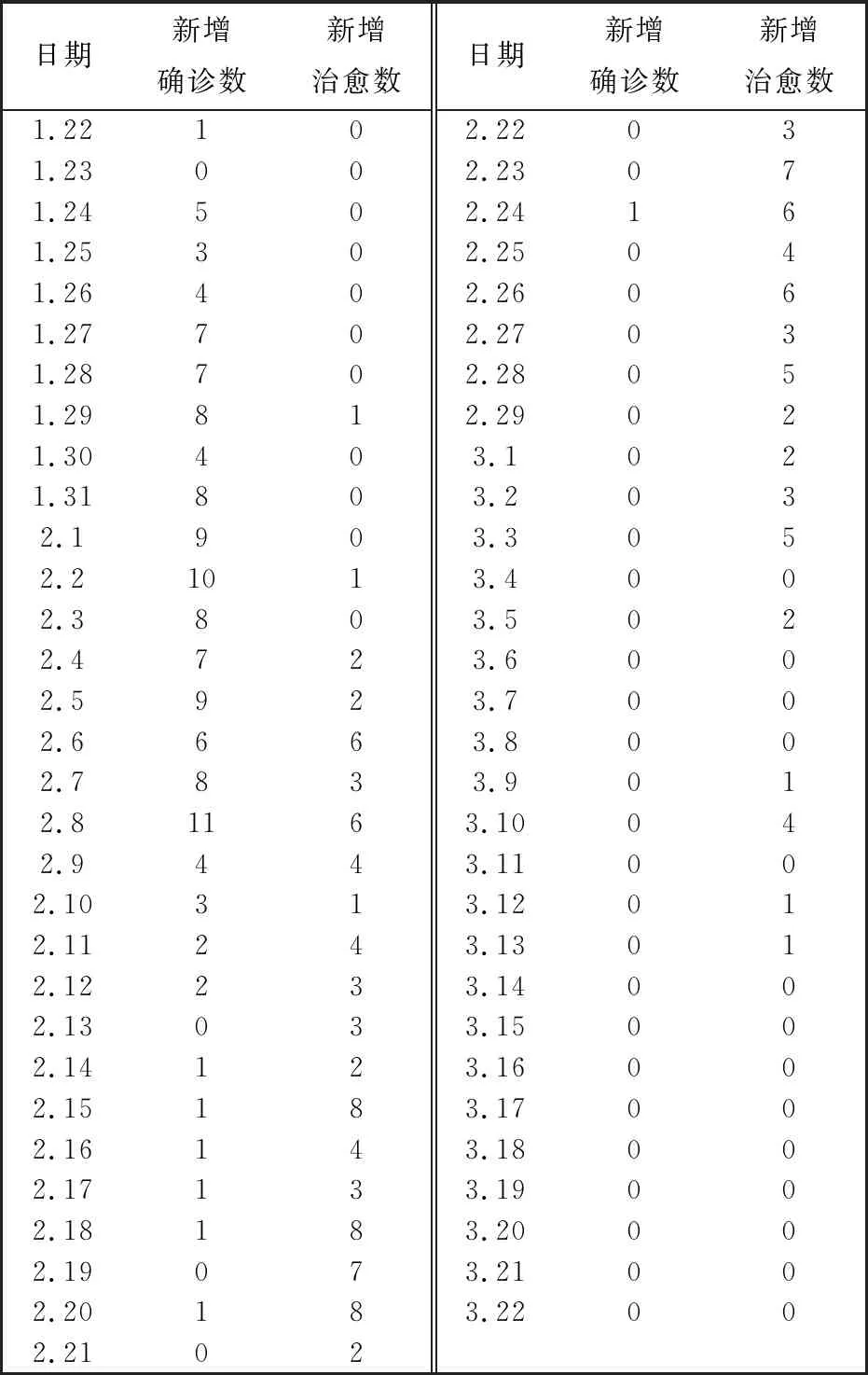
表1 山西省每日疫情数据
1.2 基本假设
建立差分方程前, 提出一些基本假设:
1) 模型不考虑自然出生和自然死亡等因素;
2) 感染者在潜伏期内出现症状为有症状感染者, 此类人群确诊后被医院收治. 但不是所有的感染者一出现症状就住院, 因此, 存在延迟效应;
3) 部分感染者经过潜伏期后有轻微症状或未出现症状, 未被医院收治, 此类人群为无症状感染者, 被发现后需隔离14天, 核酸检测通过后解除隔离;
4) 由于政府防控严格, 部分潜伏者未出现症状就被隔离, 在隔离期内出现症状后住院;
5) 住院的病人被医院收治一段时间后治愈或死亡;
6) 在就医和隔离期间没有传染性;
7) 患者治愈后不再被感染.
1.3 变量说明
根据COVID-19传播特征和基本假设, 可将人群分为六类: 潜伏者(E)、 隔离者(G)、 有症状感染者(I)、 无症状感染者(A)、 住院者(H)、 移出者(R).具体说明如下:
Et: 第t天新增潜伏者, 具有传染性;
Gt: 第t天已感染, 处于潜伏期但被隔离的人群;
It: 第t天新增有症状感染者, 经过潜伏期后出现症状, 具有传染性;
At: 第t天新增无症状感染者, 经过潜伏期后未出现症状, 具有传染性;
Ht: 第t天新增住院者;
Rt: 第t天新增移出者, 指当天治愈出院和死亡人数之和;
HI: 有症状感染者中的住院人数;
RH: 住院者中的移出人数;
RA: 无症状感染者中的移出人数.
1.4 模型构建
基于上述假设, 研究时间段为2020年1月22日到3月13日, 共52天, 由此构建差分方程模型
t=0,1,2,…,51,
(1)
It+1=(1-μ)·q·Et+1-T1,t=0,1,2,…,51,
(2)
At+1=μ·q·Et+1-T2,t=0,1,2,…,51,
(3)
Gt+1=l·Et+1-T3,t=0,1,2,…,51,
(4)
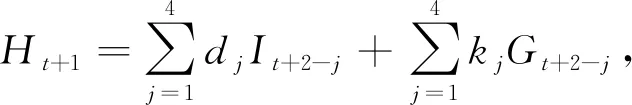
t=0,1,2,…,51,
(5)
Rt+1=RHt+1+RAt+1=Ht+1-T4+At+1-T5,
t=0,1,2,…,51.
(6)
初始条件为
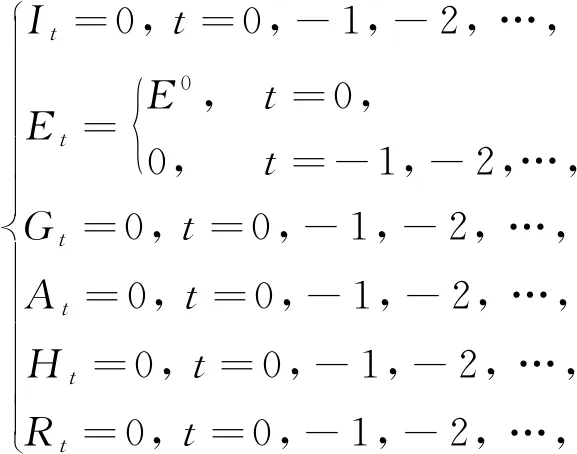
(7)
式中:t=0对应1月21日,t=-1对应1月20日,t=-2对应1月19日, 依此类推.
模型解释:
1) 由基本假设可知, 就医和隔离期间没有传染性, 因此, 第t天新增潜伏者由有症状感染者、 无症状感染者和潜伏者新传染人数三部分构成.αt、βt、δt分别为第t天有症状感染者、 无症状感染者和潜伏者的平均传染人数, 取值随时间变化.从表1确诊病例数来看, 2月2日之前新增病例呈上升趋势, 之后基本呈下降趋势, 据此将研究时间分为两个时期, 设2月2日之前的传染率分别为常数α1、β1、δ1; 2月2日之后的传染率分别为常数α2、β2、δ2.
2)μ是感染者不出现症状的概率, 用来区分有症状和无症状患者;q是潜伏者到感染者的转移率,l是隔离率.

4)每日新增移出者由RH和RA构成, 分别来源于T4天前的住院者和T5天前的无症状感染者.
5)T1为潜伏期, 潜伏者在T1天后出现症状成为感染者;T2是潜伏者转移到无症状感染者的天数;T3是潜伏者转移到隔离者的天数;T4是平均延迟天数;T5是无症状感染者被观察的天数或隔离的天数;T6是治疗期, 即感染者从住院到移出的天数;σ是传染期.
模型示意图如图1 所示.
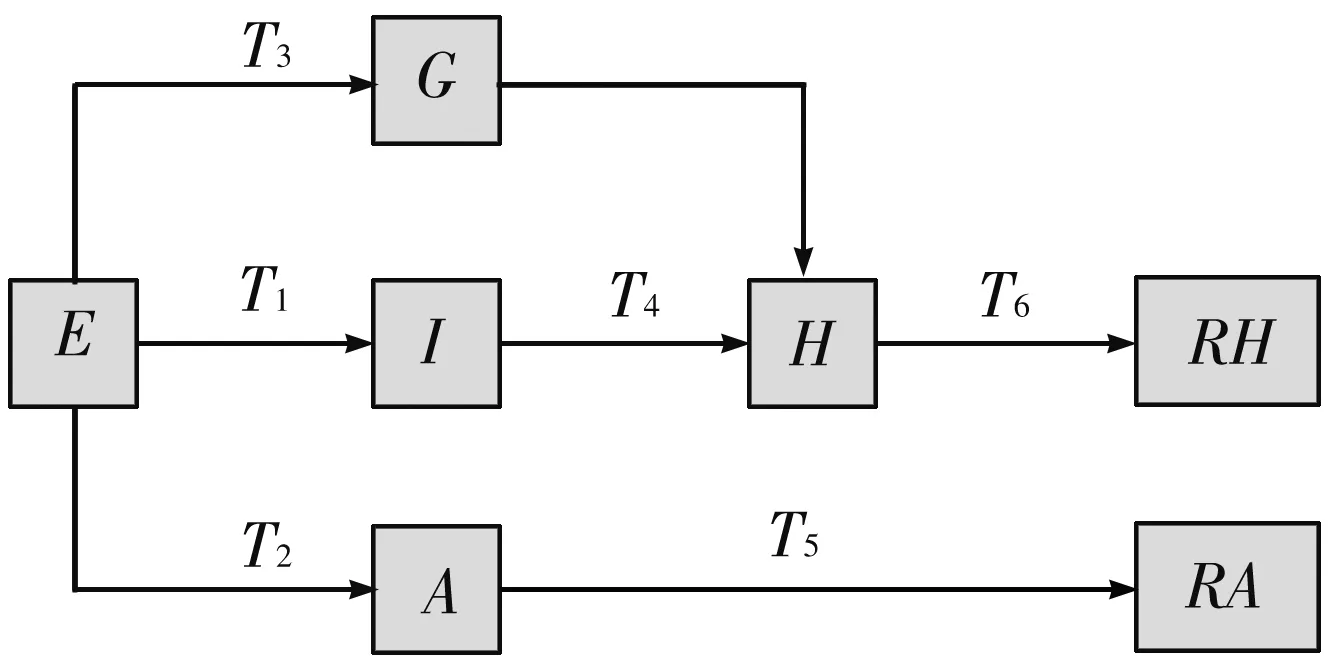
图1 模型流程图
2 参数分析
根据相关文献可将部分参数确定为常数. 其中,T1一般为3~7天[15], 这里取中位数5天; 传染期σ=T1+T4+T6=21, 即从感染病毒到康复或死亡的平均天数共21天, 则T2=σ-T5=7.隔离者经历4天平均隔离期后会确诊入院[16], 因此T3=T1+T4-4=5.由上述分析可知, 隔离者[16]和有症状感染者[14]从出现症状到入院, 分别经历4天隔离期、 延迟期. 住院者从确诊住院到出院一共经历12天治疗, 潜伏者到感染者的转移率为0.2[17]. 具体参数值设置见表2.

表2 参数值及来源
经过上述分析, 待优化参数共9个:α1、α2、β1、β2、δ1、δ2、l、E0、μ. 由表1 可知, 实际数据有限, 而山西省的治愈人数就是原来的确诊人数, 因此, 通过最小化实际确诊数与模拟确诊数的误差构建目标函数如下:
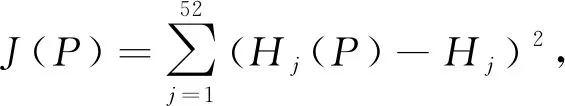
(8)
式中:P=(P1,P2,P3,P4,P5,P6,P7,P8,P9)=(α1,α2,β1,β2,δ1,δ2,l,E0,μ)是参数向量;Hj,j=1, 2, …, 52是研究时间段内医院在第j天新收治的病人数;Hj(P)是模型(1)~(7)模拟的相应值.
3 结果分析和疫情模拟
3.1 参数结果分析
基于山西省COVID-19数据, 利用MATLAB软件和最小二乘法, 对目标函数(8)进行优化, 参数估计见表3. 结果显示:

表3 参数估计结果
1) 传染率:α1<α2,β1<β2,δ1>δ2, 说明2月2日之前, 山西处于输入病例高峰期, 病例主要由初期的输入病例传染; 2月2日之后, 有症状感染者和无症状感染者传染率开始增加, 但增加幅度较小. 潜伏者由于未出现症状, 难以全部排查, 因此存在潜伏者传染率较大的情况, 随着政府管控措施的加强, 密切接触者大部分被隔离, 于是2月2日之后, 潜伏者传染率减小.
2) 隔离率为0.8, 说明山西省管控力度较强, 对抗击疫情起到较好的效果.
3) 1月21日潜伏者估计为17人, 按5天的平均潜伏期来看, 山西省在1月22日到1月 26日期间增加了13个病例, 说明估计的潜伏者较符合实际, 并且这17人中大部分是山西省新型冠状病毒的输入病例, 还有小部分是输入病例所传染的.
4) 无症状感染者比例初值由文献[18]确定, 取值0.22, 模型拟合值为0.25, 二者差距小, 说明模型拟合效果较好.
3.2 疫情模拟与预测
将参数拟合值代入模型(1)~(6)反演, 得到疫情发展模拟图, 从图2 和图3 均可看出, 1月22日至2月10日左右, 山西省疫情处在高发期, 2月11日以后, 每日新增确诊病例显著减少, 疫情趋于稳定. 模拟的累计确诊者为132人, 实际人数为133人; 模拟的累计康复者约为132人, 实际为133人, 二者的误差均为0.76%.

图2 山西省每日新增确诊病例拟合结果
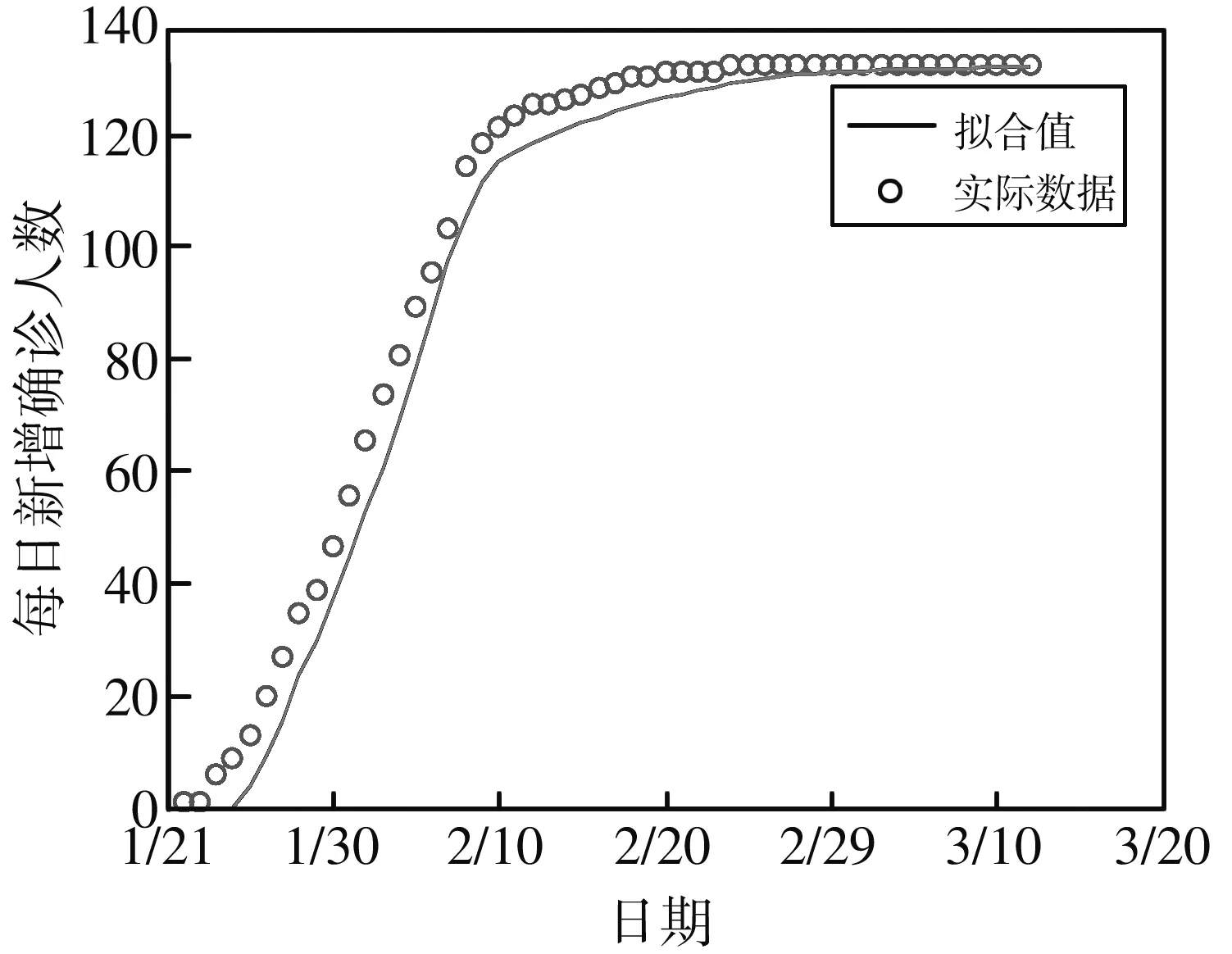
图3 累计确诊病例拟合结果
图4 为模型预测的3月14日到3月22日累计确诊图. 预测的累计确诊人数稳定在133人, 与实际累计确诊人数133人一致.
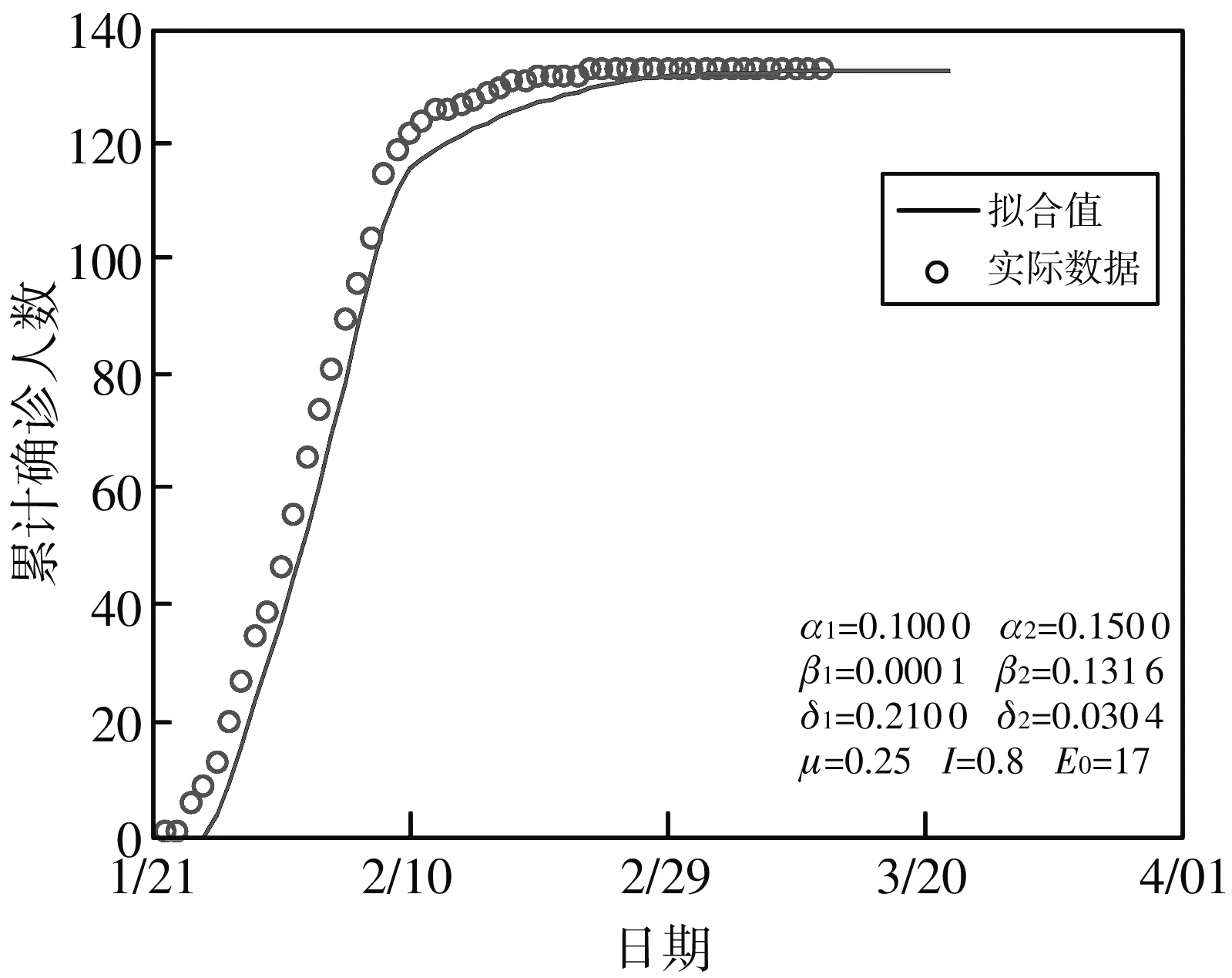
图4 优化参数下累计病例的预测
综合来看, 差分方程模型能较好地拟合山西省COVID-19疫情发展趋势.
3.3 无症状感染者的传染率参数分析
模型估计的无症状感染者约有7人,β1优化数值为0.000 1, 传染力非常小, 因此, 只考虑β2不同时的情形.图5 是β2不同时拟合的累计确诊病例. 结果表明, 无症状感染者传染率越低, 疫情控制效果越好, 产生的病例数也会减少. 当无症状感染者传染率为零时, 拟合的累计确诊数约为119人, 与实际累计病例相比减少14人, 即无症状感染者不具有传染性时, 最终染病者将降低10.53%. 由此可见, 在疫情防控中, 不仅要关注有症状感染者和潜伏者, 还要重视隐藏在人群中的无症状感染者.
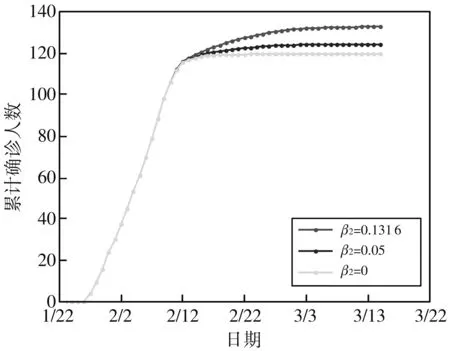
图5 无症状感染者在不同感染率下的累计病例图
3.4 政策效应评估
本文中隔离率可反映政府防控力度. 拟合隔离率为0.8, 其他参数不变时, 改变隔离率, 观察累计确诊数的假想情况, 如图6; 图7 是隔离率为0时的拟合结果. 研究结果表明, 隔离率对疫情防治有显著影响, 隔离率越大, 防控效果越好. 若无防控措施, 则研究时间段累计病例将达280人, 比实际多出1倍, 并且还会持续增长, 由此可见, 山西省防控措施对疫情起到了很好的控制效果.
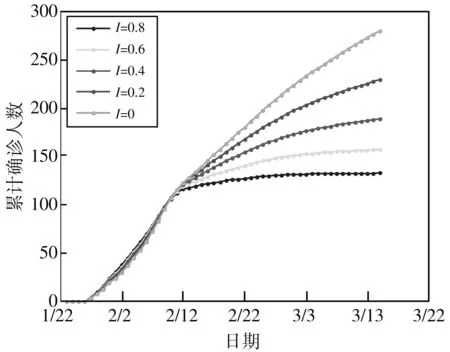
图6 不同隔离率下的累计病例拟合结果

图7 隔离率为0时的拟合结果
4 结论
本文在传统传染病模型基础上, 构建了一类具有时滞效应的差分方程模型, 分段拟合了山西省COVID-19疫情发展趋势, 分析了无症状感染者对疫情的影响, 评估了山西省防控措施的效果. 结果表明:
1) 无症状感染者的传染率并不大, 潜伏者和有症状感染者是山西省COVID-19疫情的主要传播者, 但无症状感染者也传染了10.53%的确诊者.
2) 隔离率越大, 防控效果越好, 山西省的防控措施是严格且有效的.
综上所述, 差分方程模型能较好模拟出山西省COVID-19的发展过程. 此外, 模型的参数可根据疫情发展的时间段进行调整, 使得模型更加灵活, 可应用于其他地区, 为传染病的模型提供了新的改进之处.
