基于Twin-Bennett机构固面可展开天线的优化设计

2021-06-23周怡君袁伟钦

中国机械工程 2021年11期

曾祥周怡君袁伟钦罗晨

东南大学机械工程学院，南京，211189

0 引言

随着航天事业的实施和深入，星载反射面天线逐步向大口径方向发展，但由于受运载工具有效发射容积的限制，天线、太阳能电池板等装备都需要折叠成收拢状态才能送到太空，因此星载可展开反射面天线的折叠和同步收拢方案一直是研究的热点。按照展开形式和材质的不同可将星载可展开反射面天线分为固面可展开天线[1]和柔性可展开天线[2-3]。与柔性可展开天线相比，固面可展开天线具有型面精度高、工作频率高、机械性能好等优点，更适用于工作频率要求高、口径要求小的卫星上，因此固面可展开天线的发展和应用前景广阔。

最早的固面可展开天线是美国TRW公司研制的太阳花式固面可展开天线[4]，该机构可以实现刚性天线的折叠，展开后型面的精度为0.13 mm/10 m，收拢率为44%，其型面精度高、刚度大，但是收拢能力不强，并且展开需要人工辅助。日本东芝公司在TRW公司研制的太阳花式固面可展开天线的基础上研制出了两级固面可展开天线[5]，提高了太阳花式天线的收拢能力，但是结构更加复杂。DORNIER和ESA公司共同研制了FIRST(far infrared and submillimeter space telescope)抛物面天线[6]，结构中加入了桁架，系统刚度高,收拢性能也好，但是展开后整体质量较大。剑桥大学研制了一种SSDA(solid surface deployable antenna)抛物面天线[7]，提高了收拢能力，但需要保证多个电机的同步性，型面精度也不高。2011年，俄罗斯 LABOCHKIN科研生产综合体研制的RADIOASTRON射电望远镜发射成功，其结构类似于FIRST结构[8]，该天线通过滑盘上下移动带动推杆转动从而实现盘面的展开。

国内关于固面可展开天线的分割方案和展开收拢机构设计的研究相对较少。广晨汉等[9]基于单点多折痕折纸设计了一种概念固面可展开天线，并对参数进行了优化分析。HUANG等[10]设计了一种新型花瓣式可展开天线NPDSSA(new petal-type deployable solid surface antenna)，该天线与FIRST结构类似，通过恒力弹簧实现盘面两个方向同时收拢，收拢率能达到32%。郭宏伟等[11]采用太阳花式分割方案分析了分割单元数等参数对抛物面天线的影响，并进行了建模验证。李忠杰[12]将Twin-Bennett(TB)机构与太阳花式固面可展开天线结合，分析了其运动学等一系列问题，并进行了样机试验，但是其干涉分析方案不具有普遍性，同时单电机带动联轴器单自由度收拢展开方案会导致电机受力不均从而使运动不同步。

对于型面精度，目前已知固面可展开天线的型面精度在0.13～0.5 mm/10 m，而太阳花式固面可展开天线型面精度高达0.13 mm/10 m，相对于其他类型的固面可展开天线型面精度更高。对于驱动方案，目前固面可展开天线采用的是电机联轴器、六单电机、电机滑盘和恒力弹簧等驱动方式。其中单电机带动联轴器方案因虚约束较多而使得天线实际运行过程中同步性较差；恒力弹簧驱动方案会在天线展开起始和结束时产生较大冲击，平稳性较差；而电机滑盘驱动方案稳定可靠，机构简单。

天线盘面的不同分割方案关系到收拢展开过程的干涉问题，同时会影响整体的结构设计，而驱动机构也是决定固面可展开天线展开同步性和平稳性的重要影响因素。目前使用TB机构构造固面可展开天线的研究尚未见常见的盘面分割优化方法、干涉分析和自动收拢展开方案。本文使用TB机构构造固面可展开天线，对传统太阳花式固面可展开天线的分割方案进行改进，提出一种通用的干涉分析方法，基于该干涉方法以收拢率为目标对固面可展开天线进行优化，最后根据优化结果设计单自由度伞状同步收拢驱动机构，并通过仿真和实物模型进行验证。

1 整体机构设计

1.1 固面可展开天线整体构型

首先确定固面可展开天线的盘面分割方案。传统的固面可展开天线采用图1所示的太阳花投影分割方案，该投影分割方案主要包括基圆的外接六边形，六条副副盘分割线和十二条主副盘分割线。其中，基圆半径为r1、切割圆半径为ra、抛物面直径为D。该投影分割方案将抛物面天线分割为19个单元，按照形状可以分为底盘、主盘、副盘。改进的盘面分割方案基于太阳花分割方案并且需要在整体机构确定的基础上提出。

图1 太阳花式分割方案

因为整个固面可展开天线具有对称性，所以研究其中一个运动单元即可。一个运动单元包括四个部分，分别是盘面、盘面间的铰链、主动杆和机架。盘面分别为图1中标注的5个分割盘，盘面间铰链分布如图2所示。该运动单元共有6个转动副，其中副副铰为复合铰链，主动杆通过主铰3和副副铰铰接于机架和左右副盘，用于驱动盘面的展开，而底部机架的作用是为主盘和主动杆提供铰接点并支撑底盘。

固面可展开天线的展开过程如图2所示，主副盘在主动杆和铰链的牵引下展开，当达到完全展开状态时，锁定主动杆，以保证天线展开时的刚度。

(a) 整体构型收拢状态

由图2可以看出，该运动单元仅包含转动副且构成双闭环空间过约束机构，为了满足该构型下可展开天线的单自由度展开要求，需要选择一种空间6R过约束机构。常见的空间6R过约束机构有Sarrus、Bricard、Goldberg等，而与该构型最匹配的便是基于Myard机构提出的TB机构。

1.2 TB机构及装配构型

设TB机构的每个轴线节点用i(i=1～6)表示，节点处的轴线用si(i=1～6)表示,而节点i和节点j间的连杆用lij表示。图3所示的TB机构是由两个相同的Bennett机构对称布置，共用杆l16和轴线s1、s6组成的空间双闭环6R机构。该机构由6个不共线的转动副和垂直于相邻转动副的连杆组成。CHEN等[13]推导了该机构具有单自由度时所满足的几何条件：

图3 TB机构

其中，aij表示连杆lij的长度，αij表示连杆lij两端轴线si的夹角，不妨取a12=a，a16=b。将图3中多个TB机构进行组网可构成一个大型可展开空间机构。n个TB机构可通过公用邻边形成一种单自由度的装配体，n越大装配体的运动性能越好，综合考虑质量等因素，当n=6时装配体动力学性能最优。选取α12=π/6，由式(1)可得b=2a，α34=2π/3。此时将6个TB机构的轴线s3、s4交点排列在正六边形机架的顶点，轴线s3、s4分别与正六边形机架的各边重合，同时将不同TB机构各邻边连杆l23、l45通过平面刚性板首尾固连，便可以得到图4所示由6个TB机构组成的装配体，可以证明该装配体具有单个自由度[14]。

图4 TB机构装配体

根据文献[12]，TB机构是单自由度空间6R空间双闭环机构，则图3中的TB机构各转动副轴线位置与图2中一个运动单元构型中各铰链轴线相互重合时，该运动单元具有单自由度；同理，当图4中的TB装配体每个转动副轴线与固面抛物面可展开天线所有铰链轴线重合，并且TB装配体中平面刚性板使用主盘替代时，整个固面可展开天线展开过程具有单自由度。

图2运动单元的理论模型如图5所示，TB机构的节点3和节点4固定于底盘的6个顶点，各轴线与图2铰链轴线位置重合，且均为盘面间的转动轴线。

(a) 理论构型收拢状态

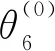
2 干涉分析与分割方案改进

2.1 固面可展开天线收拢率

固面可展开天线展开过程有两个特征位置，即完全收拢状态位置和完全展开状态位置，如图6所示。完全展开状态盘面如图6b所示，此时所有主副盘面边线重合，整体构成抛物面。不同分割方案的固面可展开天线完全展开状态是类似的，但是完全收拢状态却不相同，因此分割方案直接影响收拢率。下面定义该固面可展开天线完全收拢状态。

(a) 完全收拢特征点

如图6所示，当固面可展开天线由完全展开状态逐渐收拢时，副盘上的A点和A′点逐渐向内靠近，当A点和A′点重合时，即在坐标系ΣO0中A点纵坐标yA=0时天线达到了收拢极限，此时如果再向内收拢则两副盘将干涉。图6a定义的该状态为固面可展开天线的完全收拢状态。

2.2 副盘间干涉分析

以固面可展开天线展开至收拢状态为例，分析盘面的干涉情况。固面可展开天线内侧面为工作面，所以主副铰、副副铰均需要位于抛物面天线外侧。首先分析副盘之间的干涉情况。如图7所示，副副铰轴位于副副分割线下分两种情况。

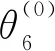
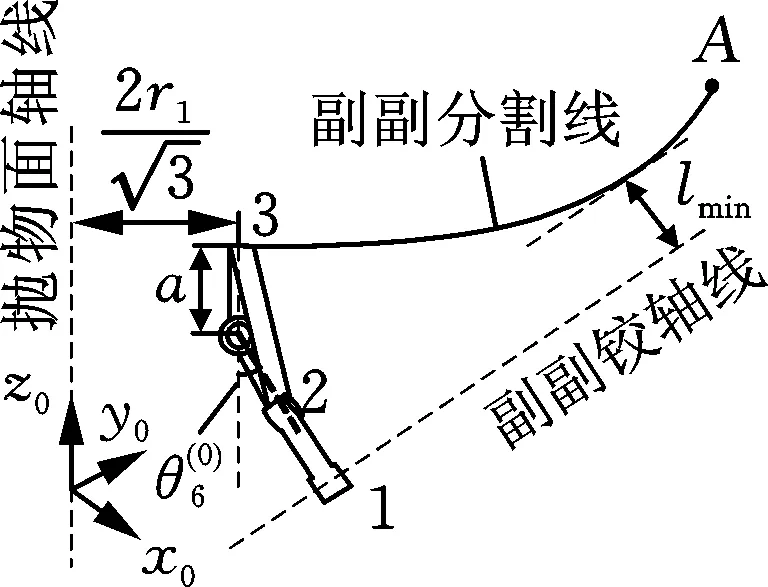
时

当理论构型的特征参数满足式(3)和式(4)时，副副铰轴线便位于副副分割线下，且副副盘面相对副副铰轴线向内收拢，即副副盘面在围绕副副铰轴线转动过程中不会干涉。

2.3 主副盘间干涉分析

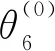
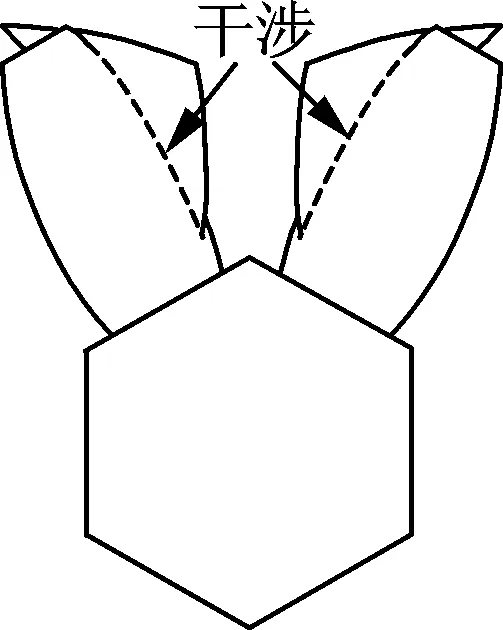
(a) 主副分割线干涉示意图

2.4 分割方案改进

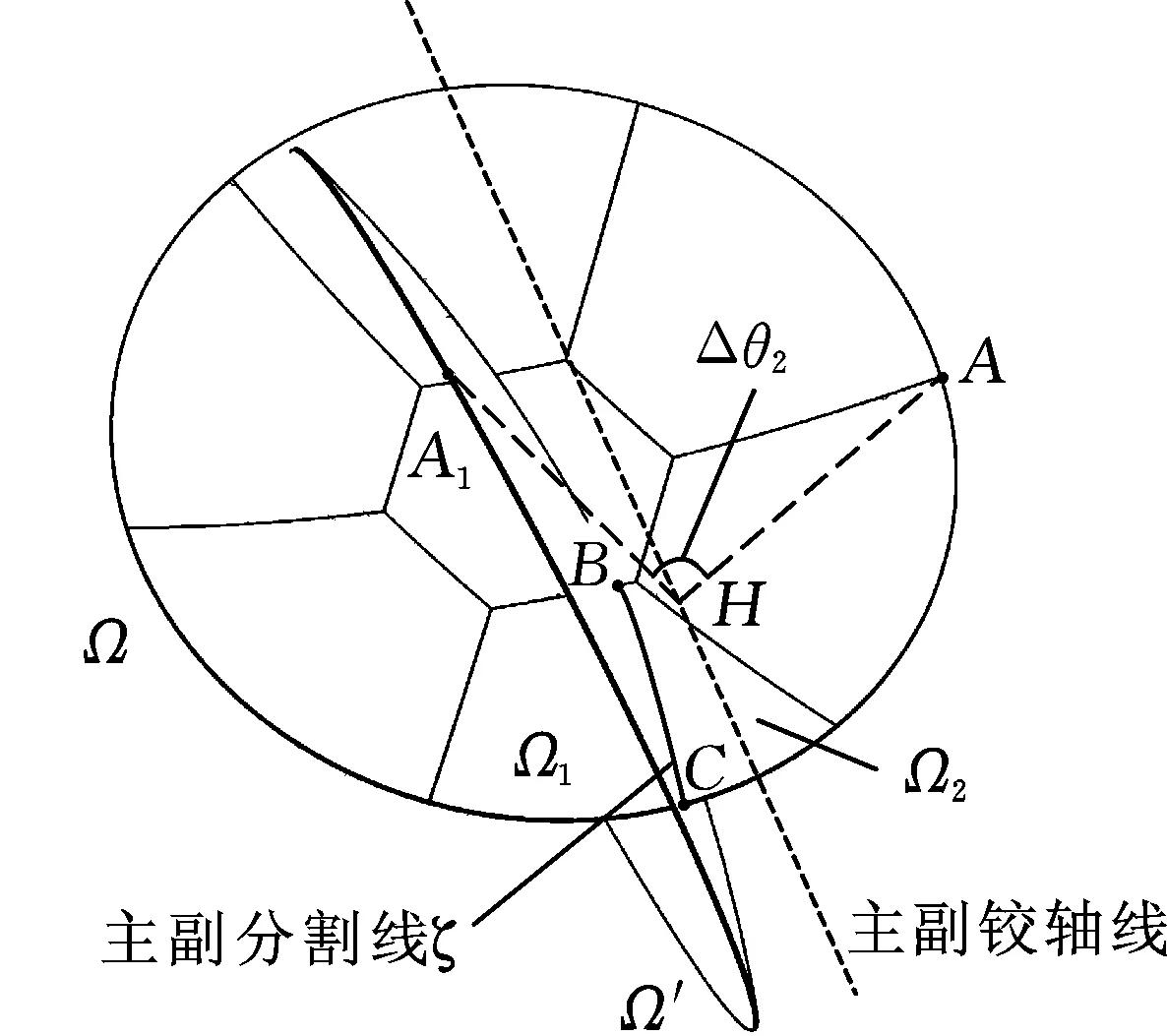
图9 分割改进方案

当考虑固面可展开天线的厚度时，因为主副盘相对主副铰链轴线向外收拢，因此需要在主副盘分割线间留出转动间隙δ。确定不干涉的最小间隙原理见图10。抛物面盘面厚度为h，分割后盘面为Ω1与Ω2，Ω2分割上顶点D点与Ω1分割下顶点E点均在以主副铰轴线为圆心、R为半径的圆上，且圆心角为φ。以Ω1为参考，Ω2分割上顶点D距离主副轴线轴心距离为s，Ω1分割下顶点距离主副轴线轴心垂直距离为h0，当转动间隙取最小时，可得

图10 分割最小间隙

当δ≥δmin时，主副盘面之间不会发生干涉。

3 固面可展开天线数学建模

3.1 理论构型数学建模

基于天线结构的设计需求，抛物面口径D=1500 mm，盘面厚度h=5 mm，抛物面方程为

x2+y2=5000z

(6)

如图11所示，在固面可展开天线完全展开时的理论构型上建立三级坐标系，其中ΣO0为固定于底盘中心的固定坐标系，各轴方向如图11a所示。ΣO1、ΣO2为动坐标系，旋转轴均为z轴,z1轴与s3轴线重合，x1轴与杆l23轴线重合，z2轴与s2轴线重合，x2轴与杆l12轴线重合。y1轴与y2轴根据右手定则确定。

(a) ΣO0与ΣO1示意图

通过TB机构的参数关系，可以得出θ6与θ3之间的关系:

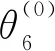
为了构造转动关节的运动旋量，注意到

取轴上的点

由此产生的运动旋量为

由Rodrigues公式和指数积公式可得

其中式(9)～式(13)中各参数具体含义见文献[15]。

完全展开状态下A点的齐次坐标可表示为

完全收拢状态下A点齐次坐标为

将式(7)～式(14)及A0代入式(15)可得

(16)

由此确定了固面可展开天线完全展开和收拢状态与设计参数的对应关系。下面确定主副分割线和收拢状态时决定收拢率的特征点B、C的坐标。

初始抛物面方程Ω齐次坐标表示为

Ω=(x,y,z,1)T

其中，x,y∈[750,750]。

旋转后抛物面方程Ω1齐次坐标表示为

即

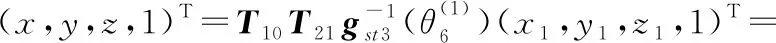
(19)

其中，f1、f2、f3为x1、y1、z1的函数。则主副分割线方程为

因为B、C两点位于主副分割线上，故天线完全展开时主副盘上的特征点B、C齐次坐标为

天线完全收拢时,B、C两点坐标分别为

将式(14)和B0、C0坐标代入式(21)，根据式(2)便可以确定固面可展开天线的收拢率η。

3.2 优化模型的建立与求解

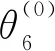
式(22)中第一个式子为目标函数；第二个式子为主副盘正确分割约束条件，目的是避免出现图12所示的情况；第三个式子为2.2节中副副盘面不发生干涉的约束条件。

图12 主副盘分割线错误方案

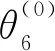
图13 优化迭代过程

4 同步机构及驱动设计

4.1 伞状同步机构设计

固面可展开天线由6个相同的TB机构控制，每个TB机构均有一个主动杆l16，为了保证6个主动杆l16同步运动，即整个可展开天线实现同步展开，使用曲柄滑块机构来驱动TB机构的主动杆l16。曲柄摇杆与TB机构连接的示意图见图14a，图中曲柄滑块机构中滑块8为主动件，其自身的直线运动转化为曲柄l67的旋转运动，因为曲柄l67与TB机构固连，所以曲柄l67的运动转化为TB机构主动杆l16的运动，从而带动主副盘的收拢展开运动。

因为整个机构具有对称性，所以需要6个相对抛物面轴线中心对称的曲柄滑块机构同时驱动抛物面天线。选取丝杠模组为驱动机构，6个滑块固定于丝杠模组的滑盘上，构成图14b所示的伞状同步展开机构。根据优化结果和装配空间需求，选取滑块与抛物面轴线的距离e=70 mm，连杆l78长度为350 mm，曲柄l67长度为24.04 mm。

(a) 滑块TB机构示意图

4.2 驱动机构运动规律

可展开天线展开和收拢是一对相逆的运动，为了方便在仿真模型中测量收拢率，研究驱动运动规律和运动学特征时均选取可展开天线从完全展开到完全收拢这一过程。

由4.1节可知，固面可展开天线收拢由图14中的6个滑块8组成的滑盘控制，所以确定驱动规律等同于确定滑块8的运动规律。为了使固面可展开天线展开过程中不产生冲击，主动杆l16在收拢开始时需要缓慢加速，收拢结束时需要缓慢减速，整个过程中保持平稳转动。设整个固面可展开天线完全收拢耗时t=20 s。根据平缓运动约束使用多项式规律拟合TB机构主动杆l16转角θ6：

θ6(t)=a5t5+a4t4+a3t3+a2t2+a1t+a0

(23)

从图14a分离出曲柄滑块机构，如图15所示,由4.1节可知，该曲柄滑块机构为负偏置曲柄滑块机构。

图15 曲柄滑块机构

根据复数矢量法可以得出

对时间求导可得

因为TB机构中主动杆l16与曲柄摇杆中曲柄l67固连，所以θ6=θ7，将优化结果和式(23)代入式(24)、式(25)可以得出滑块的运动规律，如图16所示。当固面可展开天线从完全展开状态运动到完全收拢状态时，滑块行程为47.41 mm，整个收拢过程没有冲击。

(a) 滑块位移

5 建模与仿真

将SolidWorks中建立的模型导入ADAMS，为各关节加上运动副，盘面和推杆都采用碳纤维增强复合材料，表面涂覆反射涂层，仿真结果如图17所示。将4.2节中滑块的位移数据作为丝杠模组中螺母的驱动函数，仿真时间设为20 s，步长为0.01。经测量，固面可展开天线完全展开时直径为1500 mm，完全收拢后直径为557.12 mm，收拢率达到37.14%。仿真显示整个收拢过程平稳，不存在冲击。后处理后得到驱动力和驱动功率曲线如图18所示，主副盘面角速度、角加速度曲线如图19所示。

(a) 完全收拢状态

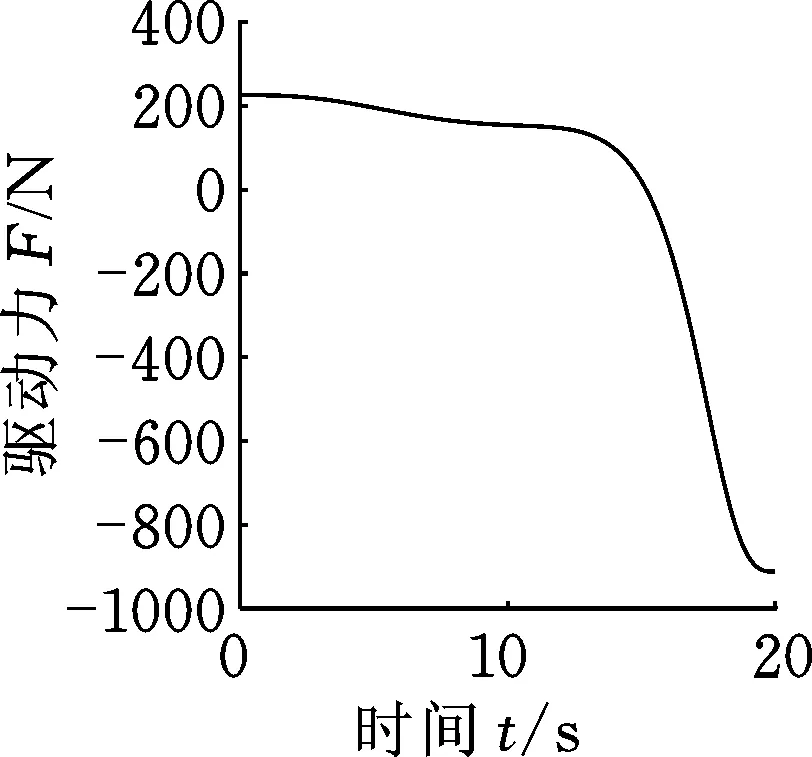
(a) 驱动力

(a) 主盘1角速度

为了验证实物模型的准确性并确定电机驱动功率，整个固面可展开天线收拢过程仿真考虑重力因素的影响。由图18可知，固面可展开天线完全展开时，电机提供的驱动力至少为226.1 N；抛物面天线完全收拢时，电机提供的驱动力至少为911.8 N；整个收拢过程电机提供驱动功率至少为919.6 W。为了保证抛物面天线维持收拢展开状态，丝杠模组要能在911.8 N的作用力下自锁。

因图1中主副盘1的收拢实质上是旋转运动，且盘面分割和驱动机构具有对称性，其他盘面与主副盘1运动特性在坐标系中的分量不同，但大小相同，所以只研究主副盘1的运动特性。

由分析知，固面可展开天线收拢过程中，主盘1围绕ΣO0的y0轴负方向逆时针转动，所以角速度全部集中于y0轴，在x0、z0轴上分量为0，大小如图19a所示，同时主盘1的角加速度大小如图19b所示。

因图1中副盘1绕空间双轴旋转收拢，且双轴轴线随时间变化，所以副盘1的角速度和角加速度在x0、y0、z0轴上均有分量，在三个轴上的分量分别如图19c和图19d所示。固面可展开天线主副盘1角速度和角加速度均无突变，整个收拢过程平稳，没有冲击。这一结果与4.2节设计时主副盘运动要求一致。

采用1∶1的比例进行固面可展开天线盘面的3D 打印模型制作，打印材质为液态光敏树脂，厚度为5 mm。从实用性和经济性角度出发，仅打印安装铰链的盘面部分和各盘面连接杆，模型的展开收拢状态示意如图20所示，实物的展开过程和图17对应的仿真结果基本一致，整个展开过程盘面运行平稳没有振动。