球面约束下四次型极小化问题的DC算法

2021-06-23周金玲

杭州电子科技大学学报(自然科学版) 2021年3期

周金玲，王洁

(1.杭州电子科技大学理学院，浙江杭州 310018；2.中国计量大学理学院，浙江杭州 310018)

0 引言

四次型极小化问题是一类特殊的多项式优化问题，是许多实际问题的数学模型。Aittomak等[1]考虑波束优化问题并将其建模为多元四次极小化模型。Aubry等[2]通过优化取实值的四次极小化模型来求解雷达信号问题。Mariere等[3]提出四次多项式优化模型并将其应用于数字通信的研究。

众所周知，多项式优化问题一般是非凸和高度非线性的，一般情况下是NP-难的。因此，多项式优化问题的求解是一个研究热点。Qi等[4]提出求解多项式全局优化问题的Z-特征值解法，Shor[5]将一般多项式规划简化为二次锥规划，Sherali等[6]提出用分支定界法求解多项式优化问题，Nie[7]提出多项式优化问题的一种精确Jacobi半定规划松弛方法。本文旨在探讨求解球面约束下的四次多项式极小化问题。

1 问题描述及转化

(1)

式中，xΤx表示向量内积。

s=i1+(i2-1)n,t=i3+(i4-1)n

(2)

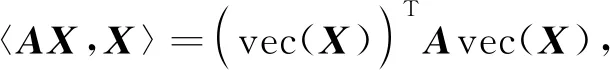
定理1令x∈Rn，则集合

U={x|x∈Rn,xTx=1}

等价于集合

V={X|X=xxT,X≥0，〈I,X〉=1,rank(X)=1}

其中〈I,X〉=trace(X)，X≥0表示矩阵为半正定矩阵。

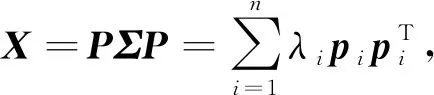
根据定理1，将问题(1)的约束条件xΤx=1转换为对矩阵X的约束，得到如下结果。

考虑优化问题：

min〈AX,X〉 s.t.X≥0,〈I,X〉=1,rank(X)=1

(3)

考虑到矩阵的秩一约束是非凸约束，为了计算方便，利用矩阵的截断奇异值分解来近似矩阵的秩。

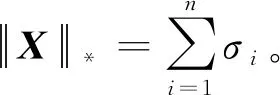
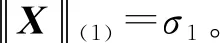
定理2[9]令X是n阶对称矩阵，则rank(X)=1等价于如下条件：

(4)

根据定理2将问题(1)的求解转换为如下问题的求解

(5)

2 DC算法

矩阵A是n2×n2对称矩阵，根据矩阵的谱分解定理，存在正交矩阵Q使得A=QTΛQ，其中Λ是由矩阵A特征值构成的对称矩阵，Q是由矩阵A的特征向量构成的正交矩阵。假设Λ对角元的前r个值大于等于0，其余值小于0。令

Λ-=diag{0,…,0,-λn2-r+1,…,-λn2}，Λ+=diag{λ1,λ2，…,λr,0,…,0}

B=QTΛ+Q，C=QTΛ-Q。因此，A=B-C，其中，B,C均为半正定矩阵，则问题(5)的求解与以下问题的求解是等价的：

(6)

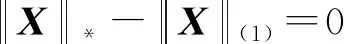
(7)

(8)

令

集合Ω={X|X≥0,〈I,X〉=1}，Ω是凸紧集，δΩ(X)是指示函数，即当X∈Ω时，δΩ(X)=0；X∉Ω时，δΩ(X)=∞。

问题(8)等价于：

(9)

式(9)中目标函数是2个凸函数的差，约束为凸集，因此问题(9)是DC规划。可利用DC算法进行求解。

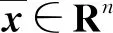
DC算法在每一次迭代的过程中利用次微分对目标函数的凹部分进行线性近似，从而得到一个目标函数的凸近似[12]。记hk(X)=h(Xk)+〈X,Yk〉，其中

矩阵次微分的计算可查阅文献[13-14]。对于问题(9)，DC算法在每一次迭代中求解的问题转化为如下形式：

ming(X)-〈X,Yk〉 s.t.X∈Rn×n

(10)

DC算法的主要步骤如下：

(1)初始化，给定对称矩阵X0，参数ε，令k=0；

(4)计算Xk+1∈argmin{〈BX,X〉+δΩ(X)-〈X,Yk〉}；

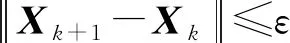
引理1[15]DC算法产生的序列{Xk}和{Yk}是收敛的当且仅当

dom∂g⊂dom∂h,dom∂h*⊂dom∂g*

(11)

定理3DC算法求解四次型极小化问题所产生的序列是收敛的。

证明根据引理1可知，只需证明式(10)的目标函数满足式(11)。

首先证明dom∂g⊂dom∂h。由式(10)可知dom∂g=Ω，dom∂h=Rn×n，显然dom∂g⊂dom∂h。

对于DC算法步骤2的子问题，利用加速投影梯度法(Accelerate Proximal Gradiet，APG)进行求解，考虑如下问题：

p(X)=〈BX,X〉-〈X,Yk〉,q(X)=δΩ(X)

(12)

根据文献[16]中对APG算法的描述，对于问题(12)的具体求解方法如下：

(1)初始化，给定对称矩阵X0，令Y1=X0，t1=1，k=1；

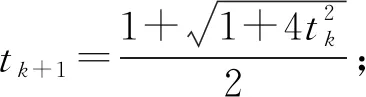
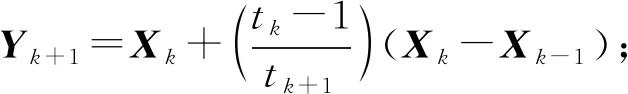
(5)若满足停机准则停止循环，否则，令k=k+1，执行步骤1。

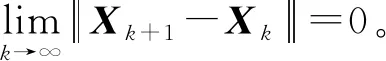
证明定理4的证明过程与文献[17]的定理3类似，这里不再赘述。证毕。

3 数值实验

将本文提出的算法和MATLAB自带优化工具包中的非线性优化函数fmincon进行比较，所有数值实验运行环境为Windows 10操作系统下的MATLAB R2016a。

为充分体现DC算法的效果，从算法的迭代次数d、所求矩阵X的秩r和计算时间t进行分析和比较。实验中，ε=1.0×10-8。

a1111=0.288 3,a1112=-0.003 1,a1113=0.197 3,a1122=-0.248 5,a1223=0.186 2,

a1133=0.384 7,a1222=0.267 2,a1123=-0.293 9,a1233=0.091 9,a1333=-0.361 9,

a2222=0.124 1,a2223=-0.342 0,a2233=0.212 7,a2333=0.272 7,a3333=-0.305 4,

对于例1中给定的张量，分别用DC算法和MATLAB中非线性优化函数fmincon计算问题(1)的最小值，实验结果如表1所示。

表1 2种算法求解算例1的数值结果

通过表1数据结果可知，给定张量的情况下，MATLAB中的fmincon函数所用时间短且迭代次数少，DC算法所求最优解则更加精确。

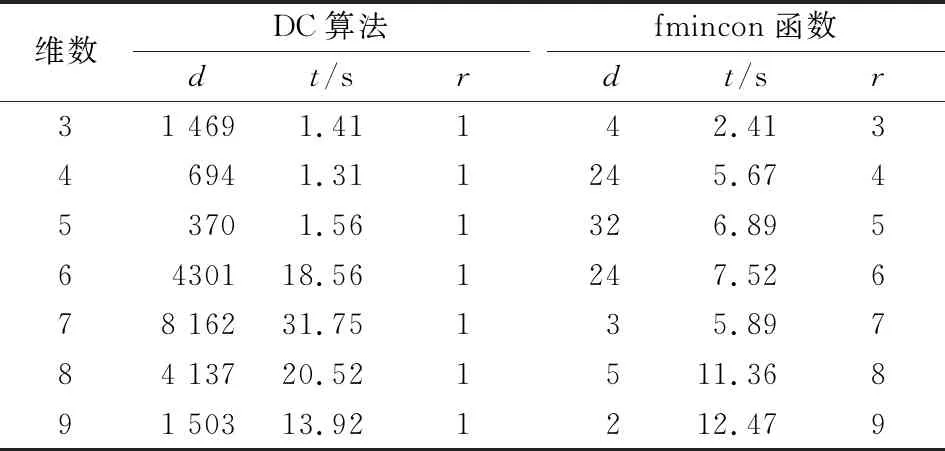
表2 2种算法求解算例2的数值结果

MATLAB中的fmincon函数是直接得到向量x，而DC算法求解过程是先求出矩阵X，再对矩阵进行特征值分解从而得到向量x。根据问题(1)中关于x的约束以及定理1可知，当DC算法求解出的X为秩一矩阵时，所得到的最优解x即为全局最优解，为了便于比较，将MATLAB求解出的x进行转换，通过内积运算得到与DC算法相对应的矩阵X，从而判断MATLAB所求解是否为全局最优解。

通过表2可以看出，和MATLAB自带优化工具包中的非线性优化函数fmincon相比较，当张量维数大于6时，fmincon函数所求最优值下降缓慢，局部最优解已经不再是全局最优解，DC算法对于全局解的求解效果更好，所求最优值更加精确，最优解为全局最优解。因为fmincon函数对初始点的依赖程度过高，而DC算法的求解与初始点无关，DC算法从任意初始点开始迭代都可以得到收敛序列。