基于长距离UWB的无人水面艇定位技术研究

杨庆生，蔡文郁，官靖凯，杨俊毅

(杭州电子科技大学电子信息学院，浙江 杭州 310018)

0 引 言

工业4.0背景下，船舶自主化航行是水路运输工具变革的重要趋势[1]。随着无人水面艇(Unmanned Surface Vessel, USV)应用场景的不断拓展，USV需要面对复杂多变的工况，不同任务阶段对导航定位精度的要求也不同，有时导航定位精度需要达到分米级[2]。海上定位技术中，使用较多的是全球导航卫星系统(Global Navigation Satellite System, GNSS)和惯性导航系统(Inertial Navigation System，INS)。高精度GNSS接收机通常结合多波段接收、载波相位信息和差分技术，但GNSS信号易受电离层异常等自然干扰及电磁信号干扰、欺骗等故意攻击[3]。同时，定位精度随卫星数量变化而波动。INS运用敏感元件测量载体在惯性空间的线运动和角运动参数，在已知初始条件下通过牛顿力学等原理融合成定位数据[4]。惯导定位的主要问题是误差随时间累积，需要辅助设备时刻进行校正。基于扩展卡尔曼滤波的GPS/INS组合定位算法结合GPS和INS的误差特性，稳定输出定位坐标，但其定位精度难以达到分米级[5]。Han等[6]在城市河道环境中，使用激光雷达传感器和即时定位与地图构建(Simultaneous Localization And Mapping, SLAM)技术得到 USV相对坐标。Ma等[7]提出一种基于雷达和卫星图像的实时定位算法，实现USV定位。目前，这些定位方法的实时性、精度仍不能完全满足USV自动导航的需求。

超宽带技术(Ultra-Wideband, UWB)拥有极宽电磁频谱，在穿透能力、精细分辨、精确测距、抗多径和抗干扰等方面具有独特的优势，广泛应用于室内高精度定位[8]。如果将UWB定位技术的通信距离进行延伸，在USV自动回收、自动回坞和自动靠岸等近距离高精度定位场景中，可以弥补GNSS定位精度不足和易受干扰等缺点。因此，本文提出一种基于大功率超宽带技术的USV定位系统，通过增加射频信号发射的功率来扩大定位范围，并提出一种基于卡尔曼滤波测距优化和几何因子最优的三边定位算法，提高了USV定位系统的精度。

1 USV定位系统设计

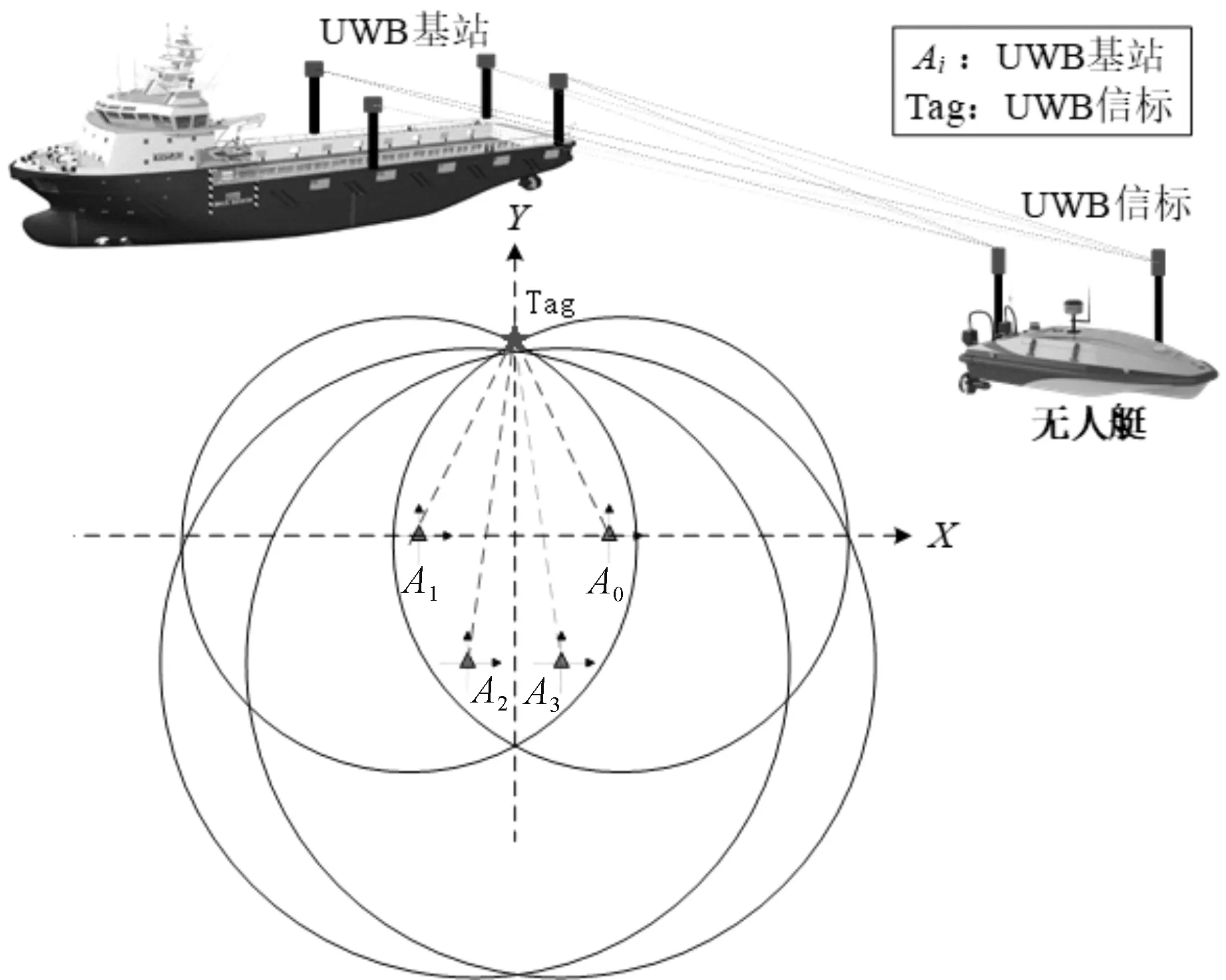
图1 USV定位系统框架

USV定位系统主要用于实现搭载UWB标签的USV定位和航向计算，由UWB基站系统和UWB移动信标系统组成。UWB信标系统测量基站之间的距离，将数据发送至USV数据处理单元，进行滤波和定位定向解算，得到二维坐标和航向。总体框架如图1所示。

1.1 系统硬件设计

UWB基站系统和信标系统由ST公司的微控制器STM32、Decawave公司的UWB测距芯片DW1000、射频功率放大模块、信号开关模块和电源转换模块组成。射频功放电路选用MACOM公司的射频开关芯片MASW-007107，将射频发送和接收分为2路：当DW1000芯片发送信号时，射频信号通过亚德诺半导体(ADI)公司的HMC326MS8G功放芯片将射频信号放大后输出；当DW1000芯片接收数据时，射频信号不经过功放芯片输入至DW1000芯片。硬件框图如图2所示。

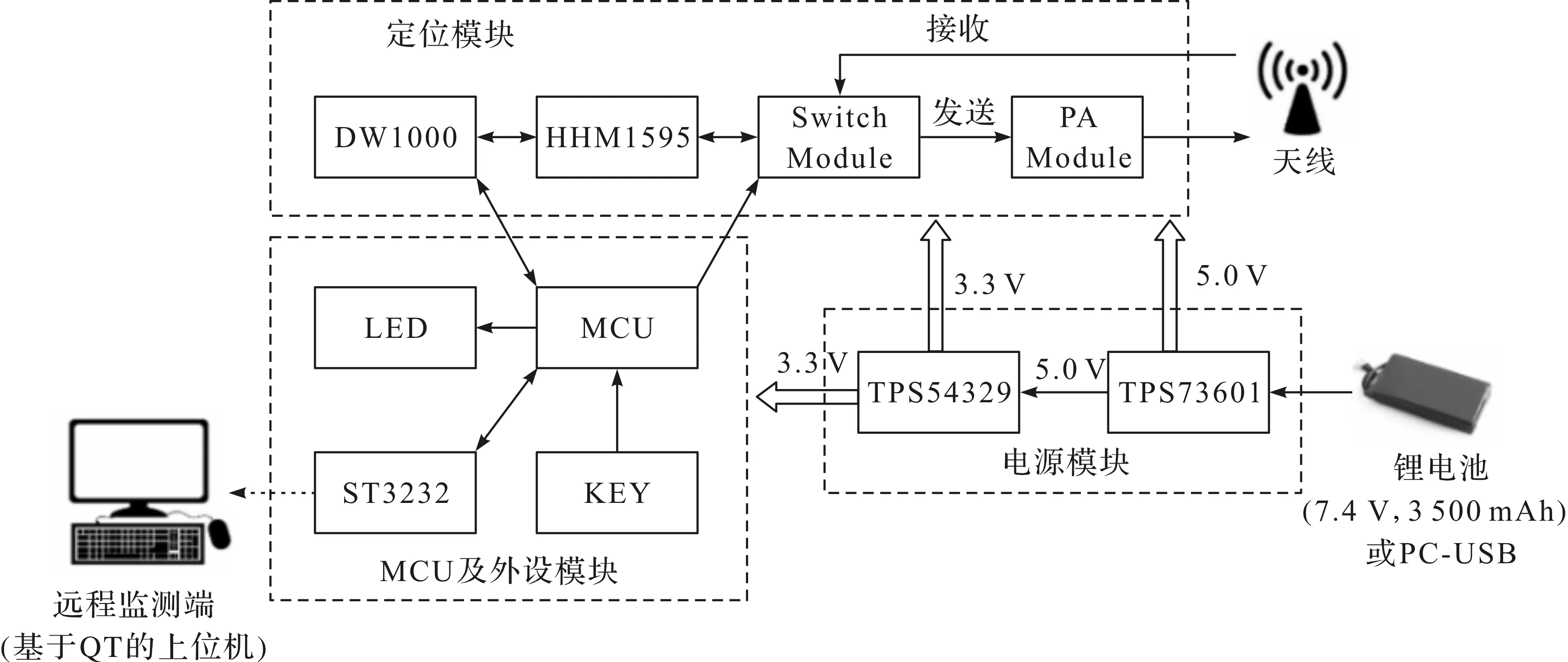
图2 定位系统硬件框图

1.2 坐标定位和航向计算

根据到达时间(Time of Arrival, TOA)测量方法定位[9]的原理可知，在二维平面下，需要至少3个已知位置的基站来进行三边定位。设3个参考节点RN1，RN2，RN3坐标分别为(x1,y1)，(x2,y2)，(x3,y3)。由UWB测得参考节点与信标节点(x,y)通信的时间分别为t1,t2,t3。由此得到：

(1)

式中，c为电磁波在空中传播速度，d1，d2，d3为信标节点到基站的距离值。将式(1)的等式两两相减，得到：

(2)

将式(2)转化为矩阵形式：

(3)

矩阵简化表示为：

AlTag=B

(4)

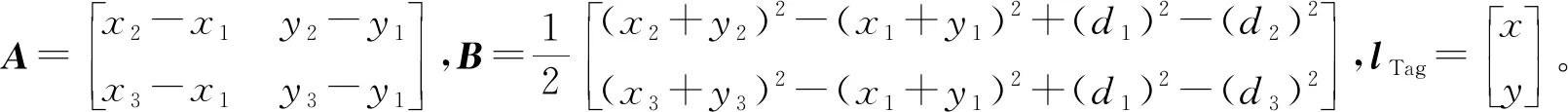
由式(4)可以得到待定位信标节点的位置坐标：

lTag=A-1B

(5)

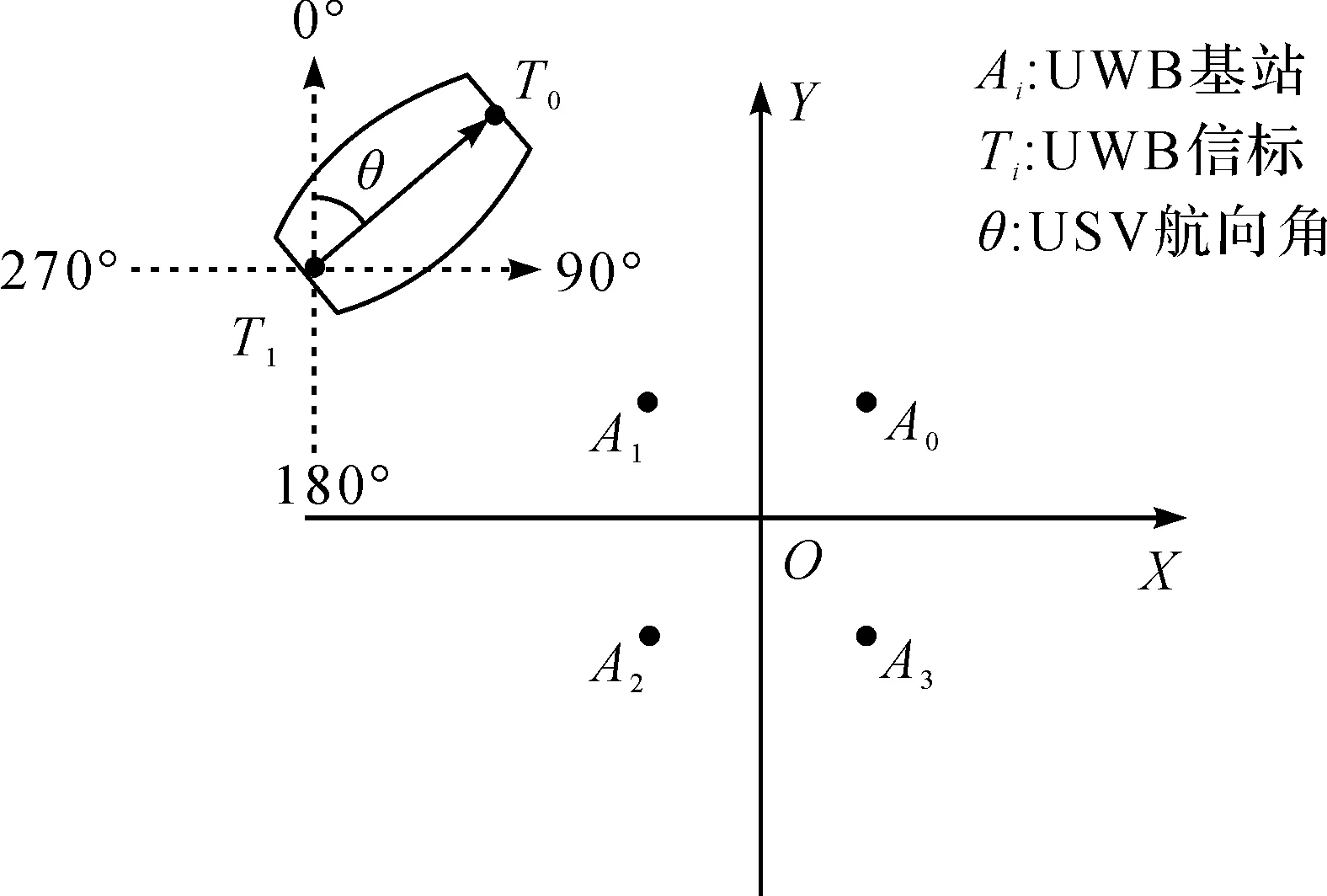
图3 USV航向角计算原理

航向角计算原理如图3所示，USV前后分别安装信标节点，以基站系统坐标系Y轴正向为0°航向角，顺时针为航向角正方向。

UWB定位系统通过TOA定位方法得到2个信标节点坐标后，计算2个信标节点X轴和Y轴位置之差ΔX和ΔY，计算公式如下：

(6)

式中，(xT0,yT0)和(xT1,yT1)分别为船艏T0和船尾T1的信标节点坐标。

USV航向角θ计算公式如下：

(7)

式中，artan为反正切函数。

2 USV定位优化方法

2.1 基于卡尔曼滤波的测距优化

USV工作在开阔水域时，定位误差主要来自随机信号干扰和测量系统误差，非视距(Not Line of Sight, NLOS)和多径传播对测距的影响较小。本文提出的USV定位系统采用线性卡尔曼滤波算法来处理原始测距数据。建立测距状态方程和测量方程，测距状态方程估算当前时刻的状态量，测量方程将原始测量值转化为测量状态量，根据最小方差准则，融合估计状态量和测量状态量，迭代计算得到当前时刻的最优状态量[10]。

在ti时刻针对一个基站的测量值建立状态方程：

(8)

并建立测量方程：

y(ti)=Bd(ti)+v(ti)

(9)

式中，y(ti)为ti时刻的距离测量值，B为测量灵敏度矩阵，v(ti)为测量误差。

卡尔曼滤波迭代方程如下：

(10)

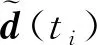
2.2 基于几何因子最优的三边定位算法

节点定位精度不仅依赖测距精度和定位算法，而且和节点相对于锚节点的几何关系密切相关，锚节点构成的多边形对其内点定位的精度要好于对外点定位的精度[11]。本文提出的定位系统针对海面环境定位，基站部署在船坞或者母船上，当信标远离基站的几何中心时，相应的定位精度出现部分下降。在多基站定位场景中，为了得到定位精度和基站几何拓扑结构的关系，引入定位几何精度因子(Geometric Dilution of Positioning Accuracy, GDOP)来描述定位误差的几何分布[12-13]。GDOP定义如下：

(11)

式中，μGDOP为定位几何精度因子，dx，dy，dz分别为x，y，z方向的定位误差均方差。

由几何精度因子定义可知，需要已知节点的参考位置，才能计算μGDOP，工程上广泛采用间接估算法，参考文献[14]提出的最大四面体体积法方法计算μGDOP近似值：

(12)

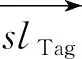
USV定位系统布设4个基站，利用冗余测距信息，选取3个基站组合的测距信息代入三边定位算法计算lTag，运用式(12)计算μGDOP值，遍历计算所有组合，选取μGDOP值最小的3个基站，所解算的定位坐标即为最终结果。

定位算法流程如图4所示。为了防止异常值干扰，原始测距数据先经过窗口中值滤波算法去掉最大值和最小值，使用均值作为最新距离测量值。最新距离值作为观测过程的新信息输入到卡尔曼滤波器，运用式(10)迭代计算预测误差协方差和卡尔曼增益，得到最优测距估计值。在定位算法流程中，比较多组μGDOP值，选取最小μGDOP值对应的基站组合的定位结果作为最终输出。

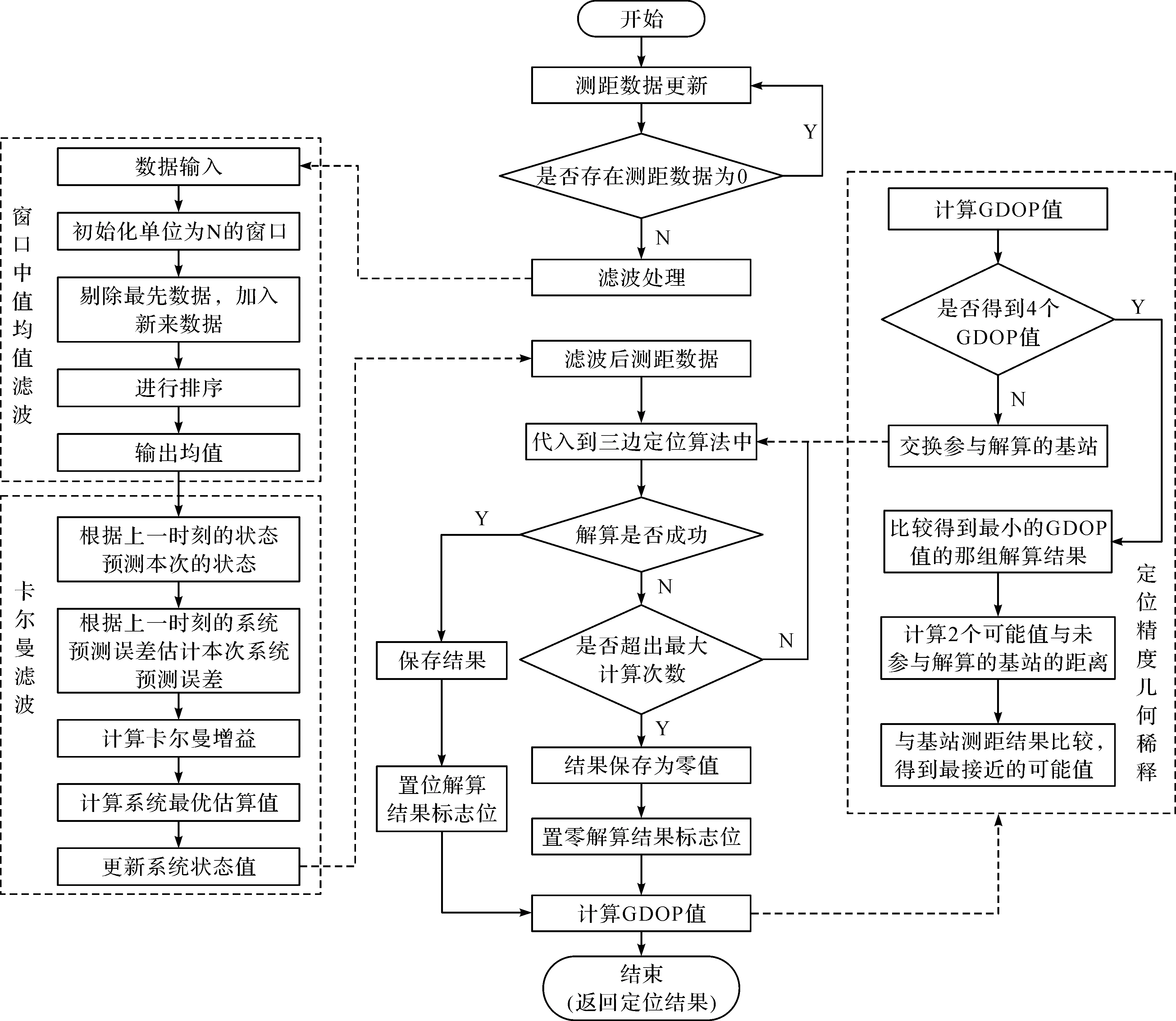
图4 定位算法流程图

3 系统测试与分析

3.1 实验环境与方法

为了验证定位系统的合理性和定位精度，在开阔湖面进行定位数据采集、实验验证和误差分析。测试方案如图5(a)所示，测试区域长宽为100 m×100 m，基站布局为梯形，以基站布局中心为原点建立坐标系，模拟USV进坞的场景。湖试场景如图5(b)所示。

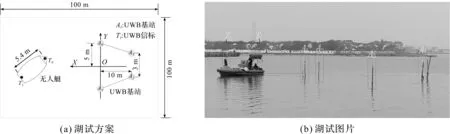
图5 湖试场景

信标T0和T1分别安装在USV的船艏与船船艉，距离固定为5.4 m，USV定位系统数据采集频率为10 Hz。使用式(13)计算同一时刻T0坐标与T1坐标距离值，计算三边定位算法和基于卡尔曼滤波测距优化和几何因子最优的三边定位算法的轨迹误差和平均绝对误差：

(13)

式中，d为船艏T0和船尾T1的信标节点的距离值，(xT0,yT0)和(xT1,yT1)分别为船艏T0和船尾T1的信标节点坐标。

(14)

式中，δ为船艏T0和船尾T1的信标节点实测距离值与真实值的平均绝对误差，di为船艏T0和船尾T1的信标节点的距离值。

3.2 实验结果及分析

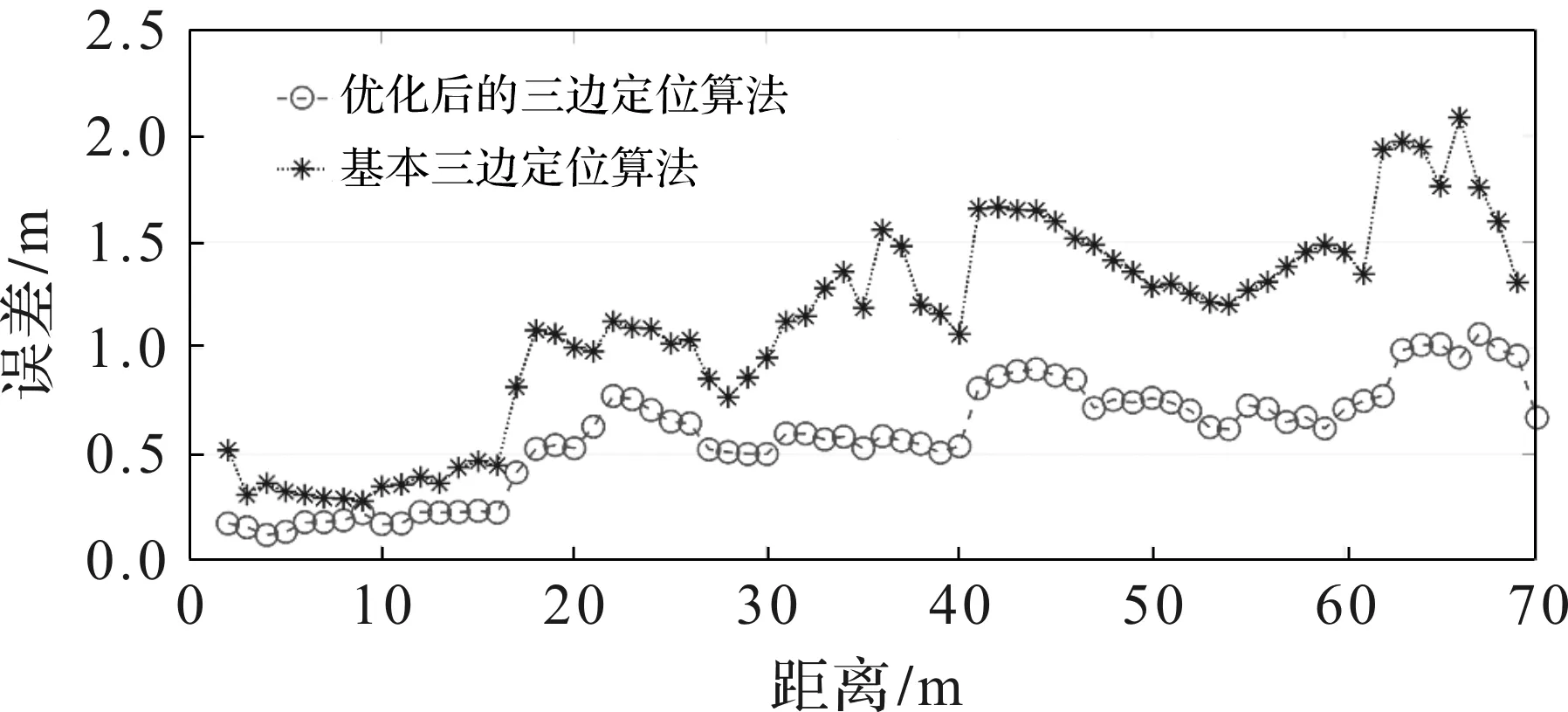
图6 不同三边定位算法的定位误差对比

为了验证本文提出的基于卡尔曼滤波测距优化和几何因子最优的三边定位算法的有效性，采集USV定位系统的10次定位测试轨迹，约10 000个坐标点的原始测距数据，分别使用基本三边定位算法和本文提出基于卡尔曼滤波测距优化和几何因子最优的三边定位算法解算定位坐标，对比2种算法解算的定位坐标的平均绝对误差。随着USV与基站之间的距离增加，未优化的三边定位算法的定位误差上升很快，本文提出优化的三边定位算法比较好地抑制了误差。在40 m范围内，优化的三边定位算法平均定位误差约为0.5 m，相比基本三边定位算法，误差下降了约35%，在40～70 m范围内，优化的三边定位算法的平均定位误差约为0.9 m，相比基本三边定位算法，误差下降了约40%。2种三边定位算法的定位误差对比如图6所示。

图7(a)是USV从起点环绕基站行驶一圈实测定位轨迹图，T0和T1分别为船艏和船艉标签的定位轨迹，使用式(7)计算航向值的结果如图7(b)所示，纵轴为对应的航向值。USV从起点行驶至终点，轨迹和对应的航向值变化连续且无异常波动，符合实际情况。

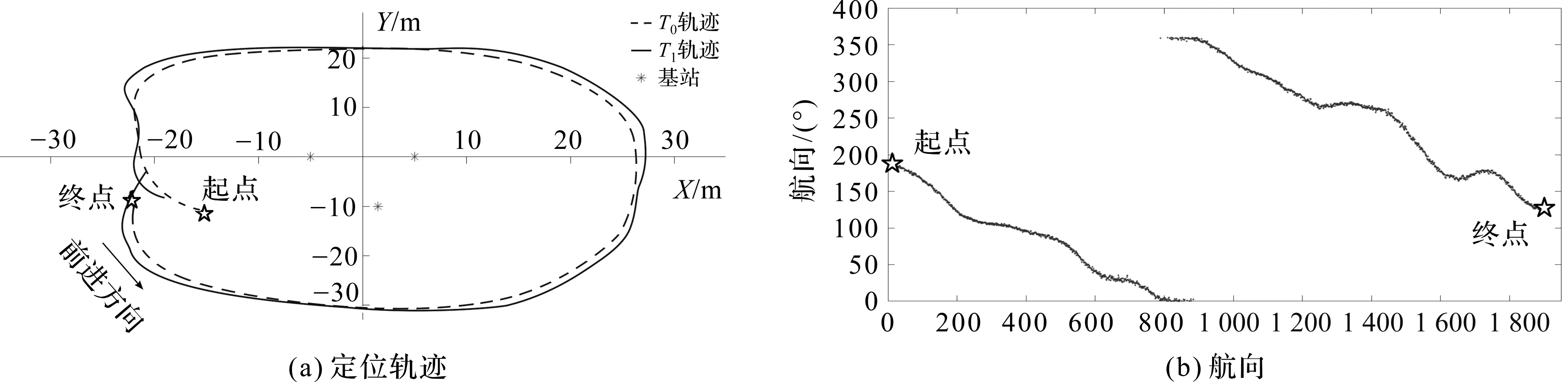
图7 定位轨迹与航向

对局部定位轨迹进行进一步放大，USV航行轨迹局部放大对比如图8所示，T0和T1分别为船艏和船艉标签的定位轨迹。从图8可以看出，本文提出优化的三边定位算法的定位轨迹与实际轨迹基本重合，且轨迹平滑，而基本三边定位算法的定位轨迹存在偏差，且轨迹波动较大。本文提出的基于卡尔曼滤波测距优化和几何因子最优的三边定位算法能有效提高定位轨迹平滑度。

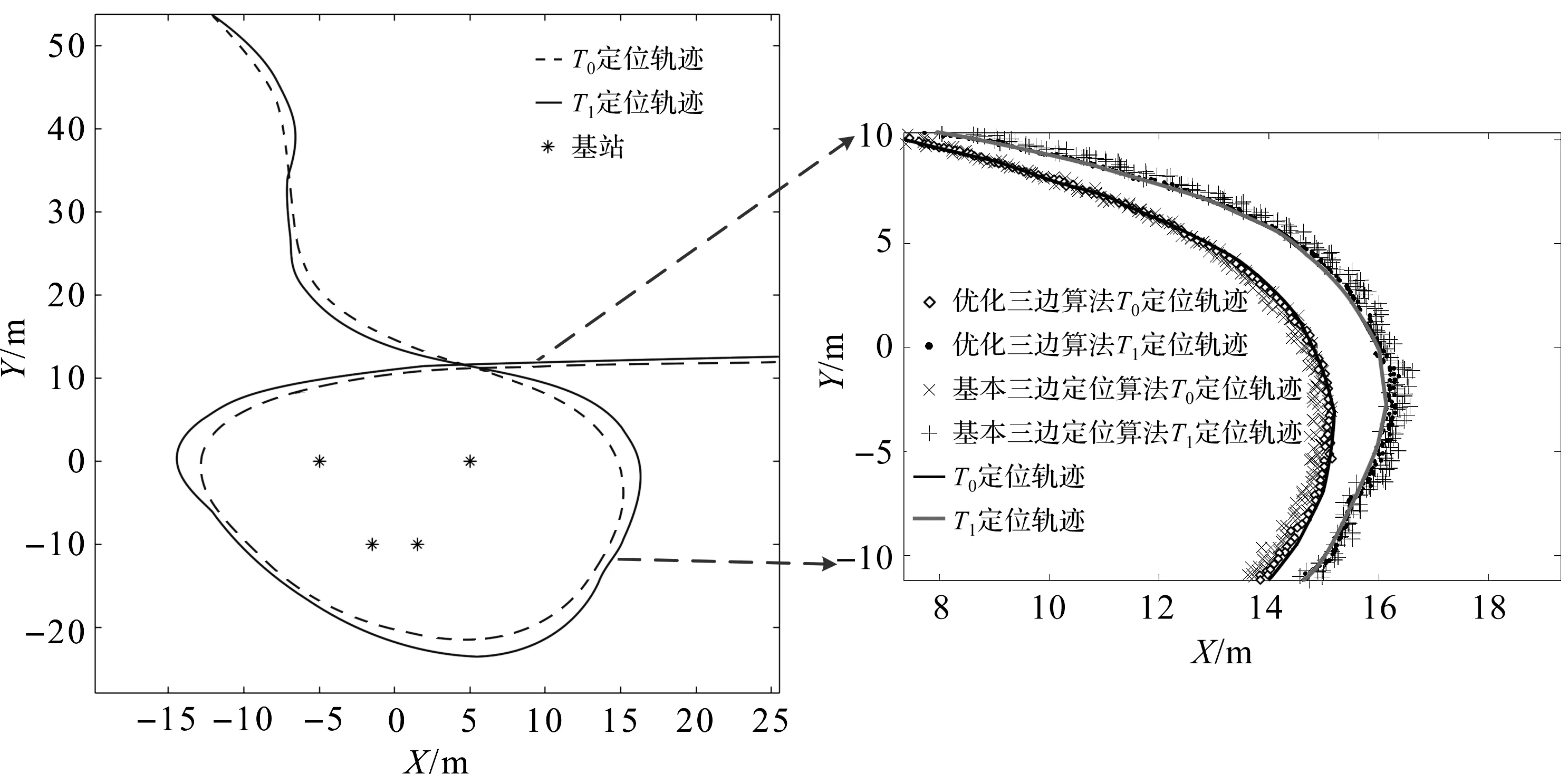
图8 USV局部定位轨迹

4 结束语

本文设计了一套在海面环境用于USV的定位系统，并提出一种基于卡尔曼滤波和几何精度因子最优的三边定位算法。在距离基站50 m范围内，本文提出的USV定位系统的定位精度在分米级，满足USV近距离高精度定位和定向的需求。后续将继续进一步研究UWB，GNSS和INS多源融合定位技术，改进USV定位系统，以提高定位系统的精度和鲁棒性。