球面纹理映射方法综述

朱庭丽

（四川大学计算机学院，成都 610065)

0 引言

在计算机图形学的发展过程中，针对纹理映射的研究一直是重点与难点之一。纹理映射是实现图形学中图形真实感表达的重要技术，它可以通过计算出每个像素点对应场景的颜色，表达出完整真实的场景。在虚拟现实、三维游戏等场景都体现出重要的应用。Catmull首次提出纹理映射的思想，为了获得物体表面生成的纹理细节，首先需要在三维物体表面进行二维参数化，再在参数化的结果和纹理平面之间建立映射关系[1]。但是在实际场景中对物体表面重新进行参数化十分困难，因为这些物体都是由非参数化面片拼接形成的多面体。所以一般采用基于中介曲面的两步纹理映射方法来实现纹理映射。两步纹理映射的方法是将二维纹理平面先根据中介三维物体的形状，投影映射到中介物体表面上，这一步映射称之为S型映射。再根据目标物体的几何形状，从中介物体曲面上映射到目标物体上，这一步映射称之为O型映射[2]。S型映射对应的常用物体中介曲面有球面、柱面和立方体。球面纹理映射法对应的中介物体曲面是球面，在二维空间的纹理坐标和三维空间的球面之间形成一种映射关系。根据球面的映射范围，可分为整球面纹理映射和半球面纹理映射。根据映射的方法可以把球面纹理映射分为基于法向量坐标变换、立体投影、透视变换、面积等比的映射方法。

1 基于整球面的纹理映射

1.1 基于法向量的整球面纹理映射

图1 基于法向量的球面映射关系

基于整球面的纹理映射是在二维矩形纹理平面上建立与之对应的球面纹理，映射范围是整个球面。为了实现映射结果，需要将矩形的长度映射为球面的纬线，宽度映射为球面的经线；其中最简单的方式是通过光照原理计算每个顶点的法向量，根据每个点平面角度生成纹理坐标。纹理坐标和球面坐标映射关系如图1所示。图中分别表示了二维纹理坐标和球面法向量坐标，纹理坐标的范围是 u∈（0，t），v∈（0，t），球面法向量坐标的范围是 x∈（-t，t），y∈（-t，t）。球面和矩形纹理平面使用反正弦函数y=sin-1x来实现两个区间之间的映射关系。由于映射函数的定义域为（-1，1），值域（-π/2，π/2），因此映射关系表示为：

其中纹理坐标用矩形虚线坐标表示，坐标轴分别用u和v表示。球面的法向量用中心的虚线坐标表示，坐标轴分别用x和y表示。t表示最后得到t*t大小的二维平面图的边长。由公式（1）和公式（2）可得逆映射关系为：

1.2 基于等面积的整球面纹理映射

矩形纹理映射到球面南北极点处时，会出现纹理汇聚现象。为了减少纹理形变，Sloan和Bier提出了三个判断准则，克服在球面纹理映射中的纹理形变：

①点的连续性：纹理平面上连续的点映射之后仍连续；

②面积的等比性：纹理平面上待映射面积为a，映射之后球面对应区域面积为k*a，k为常数；

③长宽比的不变性:纹理平面上长宽比为1:2的矩形面片和球面上对应映射的近似矩形面片仍然保持1:2 的长宽比[3]。

基于上述判断准则之一的面积等比性，Hall提出了一种基于等面积的映射算法，在该算法中球面的经度坐标与纹理横坐标u呈正比，而球面纬度的坐标的正弦与纹理纵坐标v呈线性关系[4]。在球面坐标系中，假设点 P（x，y，z）为空间中一点，M为点 P 在 XOY 面上的投影点，P的位置也可以用（r，α，β）来表示，其中r为点P到球面坐标系原点O之间的距离；α为矢量OP与Z轴正向的夹角；β为从正Z轴来看自X轴按逆时针方向转到OM所转过的角。该映射关系表示如图2所示。

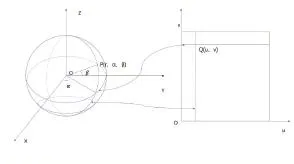
图2 基于立体投影的半球面映射

该映射关系用公式表示为：

公式中取球面半径为1，以u为常数的垂直线和球面坐标系上经度坐标为α的经线相互映射，以v为常数的水平线和球面坐标系上的纬度坐标为β的纬线相互映射。映射前的面积和映射后的面积相等，满足克服纹理形变的判断准则中的面积等比性。

1.3 基于透视变换的整球面纹理映射[5]

二维屏幕上的对应点可以通过在球面上进行三维坐标透视投影变换获得，建立球面坐标和二维纹理平面之间的映射关系。通过每个像素点保存的信息，在二维空间中通过逆映射矩阵可以求得三维球面的对应点，如图3所示。

图3 基于透视变换的球面映射

基于透视变换的球面纹理映射算法如下:

①首先在球面进行逼近精度的三角化操作;

②根据透视原理、球面模型映射区域和纹理坐标系，确定透视投影中心;

③确定组成整个球面的每个三角形面片顶点对应在纹理空间中的的坐标值[6];

④确定模型绘制球面。

利用透视变换可以快速得到球面在二维纹理空间上的对应关系。

在上述纹理映射中，二维纹理在边界处的边长会映射为球面的南北极点，在极点处会产生纹理汇聚现象，难以避免纹理形变。为了克服这一情况，Sloan和Bier建议中介面投影面使用半球面来代替整个球面，实现纹理映射变换。

2基于半球面的纹理映射

2.1 基于立体投影的半球面纹理映射

半球面纹理映射，是将两个圆形平面纹理分别映射到球面的上下两个半球面，由于映射的范围从原先的整个球面变成半个球面，纹理形变也适当的减小了。Sloan和Bier提出了一种基于立体投影的半球面纹理映射算法。该算法是通过立体投影来确定二维纹理平面与半球面之间的关系的。如图4所示。

图4 基于立体投影的半球面映射

首先将二维圆形纹理平面放置于平行于半球面的赤道面，外切与半球面的正极点，作为投影平面。选择球面的负极点作为投影中心。半球面立体投影映射是将圆形纹理平面上的圆弧映射为半球面上的纬线，平面上的径向线段映射为半球面上的经线[7]。映射公式如下：

公 式 中 的 ，p=tanαcosβ，q=tanαsinβ，α∈[0,π]，β∈[ ]0,2π。该方法的纹理在靠近赤道部分会发生较大形变，无法满足克服纹理形变的准则中的面积等比性和长宽比不变的性质。

2.2 基于面积约束的半球面纹理映射

由于曲面是不可展区面，因此球面纹理映射无法同时满足上述三个准则，不可避免的会产生纹理映射形变。基于面积等比的约束的半球面纹理映射，可同时满足点的连续性，面积等比两个准则，从而减少纹理映射中产生的形变，提高球面纹理映射的质量[7]。该方法是将二维圆形纹理平面上的某个区域映射到单位半球面上球冠表面上。其中二维圆形纹理平面的半径r≤1.0。二维纹理平面与球冠之间的映射关系如图5所示。

图5 基于面积等比的半球面映射

首先令Q点的极角和P点的经度相等，在映射过程中保持S1和S2保持一定的比例关系，即：

其中 k为待定常数，S1=πr2，S2=2π(1-cosβ)。根据公式（5），（6）可得：

令k=2，可得：

因为u=rcosα和v=rsinα，得：

当二维圆形纹理平面的半径r为1时，单位圆覆盖整个半球面。该方法通过约束面积来构造圆形纹理平面到半球面局部区域的映射关系。

3 结语

本文给出了基于整球面和半球面的纹理映射方法，通过立体投影、透视变换、面积等比的方法建立二维纹理空间和三维球面之间的映射关系。在进行球面纹理映射过程中往往会产生一定的纹理形变，如平面纹理为了适应曲面纹理，与球面吻合，常常需要对纹理进行一定的形变和从三维到二维的透视变换带来的纹理形变，造成纹理走样，不能反映出真实场景的现象。事实上，纹理映射是一个在屏幕上像素显示到二维纹理图案的映射和采样过程，当采样频率无法满足香农采样定理时，信号就会产生混叠现象，不能准确地恢复原始信号。为了避免信号的混叠现象，需要进行滤波预处理技术，但是标准卷积核并不具有适应性，从而在球面纹理映射中不能有效克服纹理走样[8]。现如今主要的纹理反走样技术有区域求和表技术、一种改进的区域求和表技术、Mip-map技术[9]都没有考虑到卷积核适应性的情况。

球面纹理映射技术虽然较为成熟，但在抗混叠等方面仍存在不少没有解决的问题，有待于进一步的研究与发展。